Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

632

=−

22 1

() cos sin ,

xt x t t

xt x t x t

ωω

ωωω

(24.1.3')

and we can write the application

()

⎛⎞

=+ −

⎜⎟

⎝⎠

00 0 0 0

12 1 2 1

;, cos sin, cos sin

ftx x x t tx t x tωωωωω

(24.1.3'')

with

×→

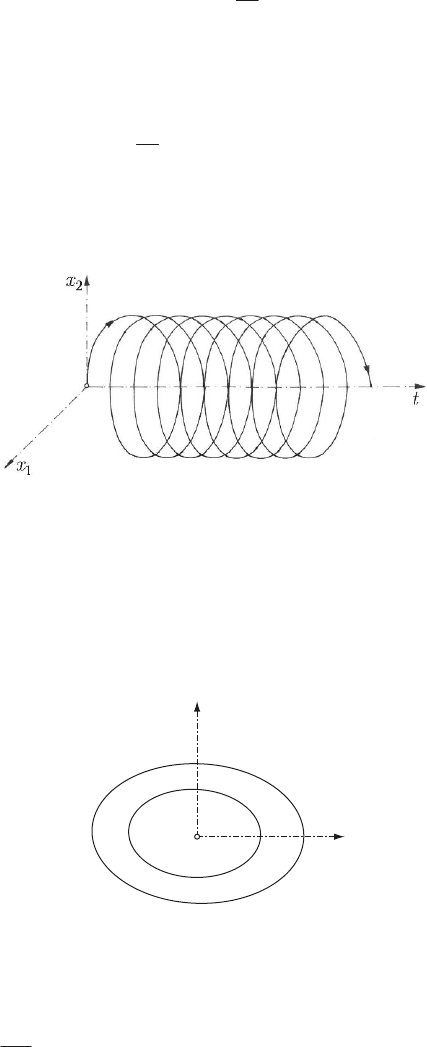
:f  . The corresponding representation in the three-dimensional

space

 is given in Fig. 24.1.

Fig. 24.1 Representation of the motion of a non-damped linear oscillator

in the three-dimensional space

×

The equations (24.1.3) lead to

=−

21 12

d/d /xx xxω , wherefrom

[][]

+= = + =

22 2 2 2 2

12 1 2

,(0)(0)constxxcc x xωω

(24.1.3''')

obtaining a family of ellipses in the phase space

 (Fig. 24.2).

Fig. 24.2 Motion of the representative point of a non-damped

linear oscillator in the phase plane

Let be now the autonomous system (24.1.1'') written in a scalar form

( , ,..., ), 1,2,...,

Xxx x i n

(24.1.4)

c/ω

Dynamical Systems. Catastrophes and Chaos

633

where

X are smooth functions (of class

C ); we can write this system also in the form

of a system of

− 1n equations

1112

d ( , ,..., )

,2,3,...,

d ( , ,..., )

xXxx x

(24.1.4')

where we supposed that

≠

() 0Xx . The solutions of this system are orbits which do

not pierce one the other. If

() 0Xx and ≠

() 0Xx , then we choose

x as

independent variable.

The point

∗

∈x

 for which

∗

=Xx() 0

(24.1.5)

is called fixed point of the system (24.1.1''); obviously, it is also a solution of the system

(24.1.4). This point is called critical point too or – in case of mechanical systems –

point of equilibrium. We notice that the system (24.1.1'') cannot be written in the form

(24.1.4') in the neighbourhood of such a point.

If, in the neighbourhood

∈

A  of a fixed point

∗

x of the autonomous system

(24.1.1''), the condition

∈x

()tA implies

∗

→∞

=xxlim ( )

t ,

(24.1.6)

then this point is called attractor; if this property takes place for

→−∞t , then the

point is a repeller.

If a solution

(; )tfx of the system of equations (24.1.1) verifies the relation

(;)(;)tT t+=fxfx for

∈t  , then this one is periodical, corresponding a closed

orbit (which can be a limit cycle too) in the phase space.

If, for

→∞t , the point x()t becomes asymptotical on a limit cycle, then this one

is a (stable) attractor, while if this property takes place for

→−∞t , then one obtains a

(instable) repulsive limit cycle.

In the frame of the above considerations, we can take again the Theorem 23.1.22 and

state (Poincaré, H., 1952).

Theorem 24.1.1 (Poincaré–Bendixon). If the integral curve

(; ) , t =∈0 fx x ,

≥ 0t

, of the system of equations (24.1.1) with

= 2n

is contained in a bounded

domain in the phase space, then a possible attractor is a fixed point or a limit cycle.

In Sect. 23.1.1.4, it has been made a study of the stability of equilibrium of an

autonomous discrete mechanical system with a single degree of freedom in linear

approximation. One obtains thus portraits of phase in the neighbourhood of the fixed

points, i. e.: nodes (which can be attractors (Figs. 23.6 and 23.9b) or repellers

(Figs. 23.5 and 23.9a)), linear attractors (Fig. 23.8b), repulsive lines (Fig. 23.8a),

saddle points (Fig. 23.7), foci (which can be attractors (Fig. 23.10b) or repellers

(Fig. 23.10a)) or centres (Fig. 23.11). The case in which the autonomous discrete

mechanical system has

n degrees of freedom has been considered in Sect. 23.1.1.5.

MECHANICAL SYSTEMS, CLASSICAL MODELS

634

Let be the differential equation

′

=− −mx kx k x

  ,

(24.1.7)

corresponding to the motion of a particle acted upon by an elastic force

−kx

and by a

force of viscous damping

′

 ; we can write in the phase plane

122 1 2

,2,,2

xxx px xp

λλ

′

==−− = =

(24.1.7')

with the solutions

−−

=−=−

11 121 2

ecos( ), ecos( )

xA t xA t

λλ

αϕ αϕ

(24.1.7'')

where the constants

12 1

,,,AAαϕ and

ϕ are determined as functions of ,,mkk

′

and

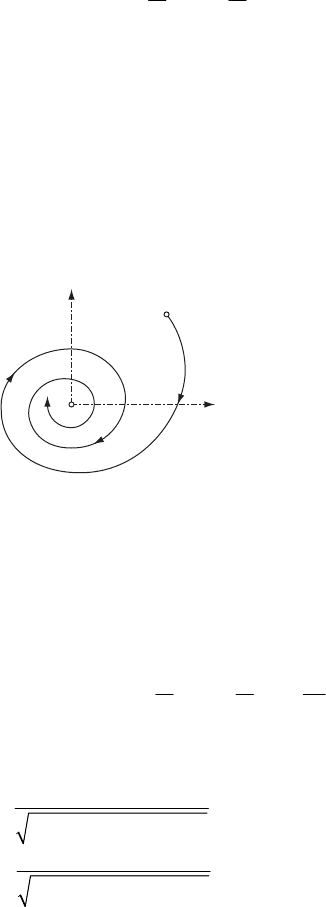
of the initial conditions. The trajectory in the phase plane has the form of a spiral; we

notice that

→

0x and →

0x for →∞t and for any initial conditions (Fig. 24.3).

The origin

O is a fixed point, i. e. an attractor, its existence being a characteristic of the

damped motions. In this case, the whole phase is the basin of the attractor.

Fig. 24.3 Motion of the representative point of a damped linear oscillator in the phase plane

Adding a perturbing force, we obtain the equation

′

=− − +

cosmx kx k x F tω  ,

(24.1.8)

which leads, in the phase space, to the system of differential equations

′

==−−+ = ==

122 1 2

,2cos,,2,

xxx px xq tp q

mmm

λω λ ,

(24.1.8')

with the solutions (

< pλ )

()

−

=−+ −

−+

=−− −

−+

11 1

22 22

21 2

22 22

ecos( ) cos( ),

ecos( ) sin( ),

xA t t

αϕ ωψ

ωλω

αϕ ωψ

ωλω

(24.1.8'')

Dynamical Systems. Catastrophes and Chaos

635

where the constants

12 12

,,,,,AAαϕ ϕ ψ are determined as functions of

,, ,mkk F

′

and of the initial conditions. The periodic particular solutions

() ()

−+ −+

22 22 22 22

ωλωωλω

(24.1.9)

lead, by eliminating the temporal variable, to a closed trajectory (an ellipse)

(24.1.9')

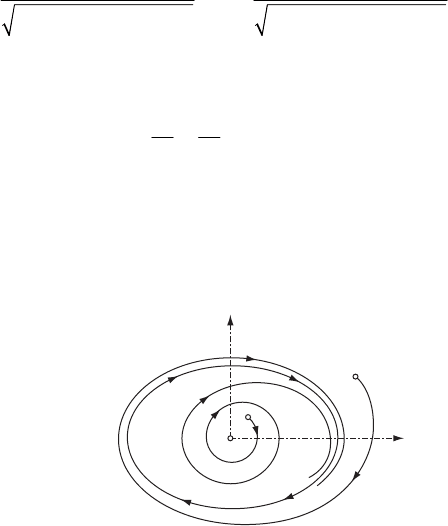
We notice that for

→∞t the solutions (24.1.8'') tend to the solutions (24.1.9); hence,

starting from an initial point

, interior or exterior to the ellipse, the trajectory tends to

the latter one. In this case, the attractor is of limit cycle type, its basin being the whole

phase plane too (Fig. 24.4).

Fig. 24.4 The attractor of limit cycle type of a damped linear oscillator acted

upon by a perturbing force in the phase plane

As we know (see Sect. 8.2.2.4), by the superposition of two harmonic vibrations

(periodic motions) with periods which have not a common multiple, one obtains a

non-periodic (pseudoperiodic) motion, which – after H. Poincaré – admits a

representation in a three-dimensional phase space; starting from an arbitrary initial

point

P , the trajectory tends to be an envelope on a torus in

 for →∞t . In this

case, the attractor is a dense curve on the torus.

In general, in the case of the system of differential equations (24.1.1), we assume

that the initial point

= x

()PP belongs to a set of points

D ⊂  and that for

→∞t the solution x()t tends to a set of points A . We say that the set A is an

attractor for the solutions which start from the set

D ; the maximal set

max

D for which

→PA for →∞t if ∈

max

PD is called the basin of the attractor A . The set A

can be a point, a limit cycle in

 or in

 or a hypertorus in

 . If →PA for

→−∞t , then the set A is a repeller (a repulsive set).

A study of the non-linear systems of differential equations and their connection to

linear systems is given in Sects. 23.1.2.3 and 23.1.2.4.

MECHANICAL SYSTEMS, CLASSICAL MODELS

636

Let be the autonomous system of differential equations

=+ ∈ ≠

Ax f x x A

(), ,det 0



(24.1.10)

with

=fx xlim | ( ( ) | / | | 0 for →x|| 0, the fixed point being = 0x . H. Poincaré

showed that, if

= 2n , then any singular point of the linearized system of differential

equations (with

=fx() 0 ) has a corresponding singular point, of the same type and

with the same type of stability, for the system of non-linear differential equations; but

we mention that to a centre of the linearized system corresponds a centre or a focus for

the non-linear one. In the general case (for an arbitrary

n ) one can show that = 0x is

an attractor (repeller) for the non-linear system too. As well, if the matrix

A has an

eigenvalue with a positive real part, then

= 0x is no more attractor for the non-linear

system.

If the matrix

A is singular ( =Adet 0 ), then – beside the critical point

∗

x – there

exist in

 also other manifolds which have this property (straight lines, planes etc.).

The dimension of these manifolds is equal to the dimension of the nucleus of the

matrix

dim ker nr=−A , (24.1.10')

where

n is the order of the matrix, while r is its rank. We can say that these manifolds

correspond to some positions of indifferent equilibrium in the case in which the

dynamical system is a mechanical one.

A mechanical system can remain in equilibrium an indefinite time at a critical point

∗

x if no perturbation intervenes; such perturbations cannot be avoided, because –

practically – one cannot take into account, in the mathematical modelling, all the factors

which determine the behaviour of the mechanical system. Obviously, a good

mathematical model is that in which one takes into account the most important factors;

the factors which we neglect lead, in general, to very small perturbations, which may be

internal perturbations (called noise) or external perturbations (resulting from factors

external to the dynamical system). The importance of the study effected in the

preceding chapter on the stability of the equations of equilibrium is thus put in

evidence.

Let be, e. g., Helmholtz’s oscillator

(24.1.11)

which leads to the system of differential equations of first order (

xx,

d/dxxt)

==+

211

xxx

(24.1.11')

Dynamical Systems. Catastrophes and Chaos

637

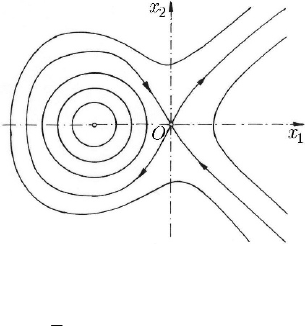
with the fixed points

12 12

( , ) (0,0), ( , ) ( 1,0)xx xx

∗∗ ∗∗

==−; a linear analysis shows that

the first fixed point is a saddle point, while the second one is a centre (Fig. 24.5). A first

integral (the mechanical energy integral) is of the form

Fig. 24.5 Representation of the motion of Helmholtz’s oscillator in the phase plane

−− = =

22 3

21 1

,const

xx xCC

(24.1.11'')

corresponding the orbits in the figure. The curve corresponding to

= 0C passes

through the point

−(3/2,0) and is called homoclinic orbit.

24.1.1.2 Non-autonomous Systems of Linear Differential Equations with a Control

Function

We consider now a non-autonomous system of differential equations (24.1.1),

(24.1.1') of the form

=+xAxBv()t



(24.1.12)

where

A and B are constant matrices and =vv()t , with

⎡⎤

⎡

⎤

⎡⎤

⎢⎥

⎢

⎥

⎢⎥

⎢

⎥

⎢⎥

===

⎢⎥

⎢

⎥

⎢⎥

⎢

⎥

⎢⎥

⎢

⎥

⎣⎦

⎣

⎦

⎣⎦

AB v

11 12 1

21 22 2

nn m

bb b

aa a

bb b

aa a

bb b



 







;

(24.1.12')

the matrix

A is a square one of order n , the matrix B is a rectangular matrix with n

rows and

m columns, while the function v()t , called control function too, is a column

vector with

m rows.

We write the general solution of the system (24.1.12) in the form

xce()

(24.1.13)

MECHANICAL SYSTEMS, CLASSICAL MODELS

638

where we use the formal expansion

=+ + +

IAA

e ...

1! 2!

(24.1.13')

being the unit matrix, and where

[]

() (), (),..., ()

tctctct

(24.1.13'')

is a column matrix with

n rows. Introducing in (24.1.12), we obtain – easily –

−

cBv() e ()

tt, wherefrom

−

∫

xx Bv

()

() e e ( )d

ττ

(24.1.13''')

with the initial condition

==xcx

(0) (0) .

Often, the system (24.1.12) is encountered in the form

=+ =xAxBv

(),t



(24.1.14)

where

C is a constant rectangular matrix with n rows and m columns

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

11 12 1

21 22 2

cc c







(24.1.14')

while

[ , ,..., ]

yy y is a column vector with m rows.

If the eigenvalues

λ of the matrix A are distinct, then the corresponding

eigenvectors are

=u , 1,2,...,

in(column vectors with n rows); we have seen in

Sect. 23.1.1.5 that one can obtain thus the general solution (the proper mode) of the

system of equations (23.1.31').

We pass to Jordan’s canonical form by a change of function

=xT

(24.1.15)

where

=Tuu u

[ , ,..., ]

is the square matrix formed by juxtaposing the eigenvectors

(column vectors) of the matrix

A , while =

[ , ,..., ]

ξξ ξξ is a column matrix with

n rows. Introducing in (24.1.14), we get

=+ =JPv yR

(),t



ξξ ξ

(24.1.16)

where

Dynamical Systems. Catastrophes and Chaos

639

−−

===JTATPTBRTC

11T

(24.1.16')

are Jordan’s matrix of the system of differential equations, the matrix of modal control

and the matrix of modal observability, respectively.

The rectangular matrix

with n rows and m columns is called control matrix

because any zero element of it corresponds to a certain proper mode which is not

controlled by a certain component of the column vector

v()t ; if all the elements of a

row of the matrix

vanish, then a whole proper mode is not controlled. As well, the

rectangular matrix

with n rows and m columns is called observability matrix,

because any zero element of it indicates that a certain proper mode is not observable in

a component of the column vector

y ; if all the elements of a row of the matrix

vanish, then a whole proper mode is not observable.

Assuming that the characteristic equation of the matrix

has distinct roots

, the

eigenvectors being given by

==Au u , 1,2,...,

iii

inλ

, it results

[

]

[

]

[

]

== =AT A u u u Au Au Au u u u

12 1 2 1122

, ,..., , ,..., , ,...,

nnnn

λλ λ .

Observing that the matrix

−∗∗∗

=Tuuu

[ , ,..., ]

can be obtained by the superposition

of the row vectors

, 1,2,...,

∗

=u , which have the property

∗

=δuu[][]

iij

, where

, , 1,2,...,

ij nδ= , is Kronecker’ symbol, we may write

[]

∗

−

∗

⎡⎤

⎡

⎤

⎢⎥

⎢

⎥

⎢⎥

⎢

⎥

⎢⎥

⎢

⎥

⎢⎥

⎢

⎥

⎢⎥

⎢

⎥

⎣

⎦

⎢⎥

⎣⎦

TAT u u u

11 22

, ,...,

λλ λ









the Jordan matrix

J being thus a diagonal matrix.

The equations (24.1.16) can be separated in the form

ξ= ξ+ =

∑

( ), 1,2,...,

iii

ik k

pv t i nλ



(24.1.17)

where

, 1,2,..., , 1,2,...,

pi nk m==, are the elements of the matrix P ;

ξ are thus

normal co-ordinates. In this case,

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

=+ + + =

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

IJ J

e00 0

0e 0 0

e...

00e 0

1! 2!

000 e







MECHANICAL SYSTEMS, CLASSICAL MODELS

640

and the solutions of the system of Jordan normal (canonical) equations (24.1.17) are

written in the form

−

ξ= ξ+ =

∑

∫

0()

e e ( )d , 1,2,...,

ik k

pv i n

λλτ

ττ ,

(24.1.17')

where the initial conditions

(0) , 1,2,...,

inξξ== , have been introduced.

If the characteristic equation of the matrix

A has multiple roots, then appear Jordan

blocks in the matrix of the canonical differential equations; obviously, the calculation

becomes more complicated, but can be followed on the same way.

Often, the control is realized by a scalar control function

()vt , the matrix B being

reduced to a column vector

[0,0,...,0,1] with n rows and only one non-zero

element, equal to unity, the system (24.1.12) being of the form

=+ ∈xAxb x(),



 .

(24.1.18)

If the matrix

A has eigenvalues with a negative real part, then the configuration of

equilibrium is asymptotically stable; in this case, by a small perturbation

()vt , the

mechanical system (in case of such a system) tends to a configuration of equilibrium if

the perturbation disappears. If the matrix

A has also eigenvalues with a non-negative

(positive or null) real part, then the mechanical system is instable, moving much away,

for very small perturbations,

()vt , from the position of equilibrium. It is also possible

that the matrix

A be instable; in this case, the stabilization of the equilibrium is made

by control.

Replacing the operator

d/dt by D , one can write the system (24.1.18) in the form

−+ =AIxb(D) ()vt 0 ,

(24.1.18')

wherefrom

(D)()vt

−

=− −xAIb;

(24.1.18'')

it results

= (D) ( )

xf vt,

(24.1.19)

the functions

(D), 1,2,...,

fi n= , being rational functions of the operator

. We can

successively calculate

−

== =

(D) (D)

(D)(), (),..., ()

(D) (D)

x f vt x vt x vt

;

(24.1.19')

one can thus schematize the block schema of the system by circuits with feed-back. By

the application method, we choose the control function in the form

Dynamical Systems. Catastrophes and Chaos

641

=⋅+gx

() ()vt vt ,

(24.1.20)

where

[ , ,..., ]

gg g

is a column vector, while the point corresponds to a scalar

product. Replacing in the system (24.1.18), it results

=+ =+xxb Ab

(),vt





ΛΛ ;

(24.1.20')

in a developed form, the characteristic equation

−=Idet[ ] 0ρΛ becomes

−−

−

+++++=

12 1

... 0

nn n

aa aaρρ ρ ρ ,

(24.1.20'')

where the coefficients

a are linear functions of , , 1,2,...,

gij n= . Choosing

convenient roots (with a negative real part, sufficient great in absolute value), Viète’s

relations determine the coefficients

, 1,2,...,

ai n= , hence the column vector

too;

the input for the block schema of the system is only the perturbation

()vt .

One can study many interesting problems on this way, e. g., the rolling stability of an

airplane or the control stability of the artificial satellites of the Earth.

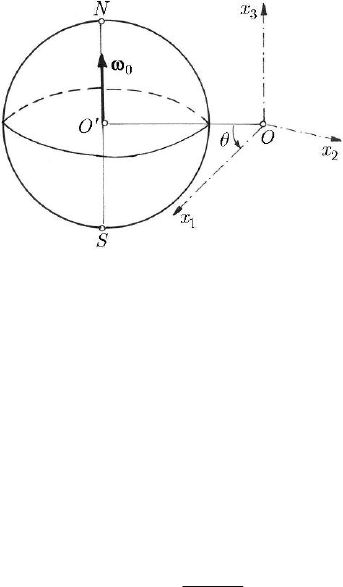
Fig. 24.6 Motion of an artificial satellite of the Earth

In what concerns the last problem, let us consider an artificial satellite of the Earth,

the mass centre

O of which moves with the angular velocity

ω on a circular

trajectory situated in the terrestrial equatorial plane (Fig. 24.6). The principal axes of

inertia

Ox and

Ox are situated in the equatorial plane, while the principal axis

is normal to this plane. Besides the attraction force of the Earth acts also a couple of

moment

=−

312

3( )MIIωθ, where

is the angle made by the

-axis with the

straight line

′

being the mass centre of the Earth; this angle specifies the small

oscillations of the satellite about the

-axis and is given by the theorem of moment

of momentum written with respect to this axis

−

+= =

222

0, 3

θθ ω



(24.1.21)