Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

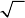
MECHANICAL SYSTEMS, CLASSICAL MODELS

682

Taking into account the above considerations on the Poincaré application, we can

make a graphic analysis in this direction; thus, Fig. 24.16a corresponds to an attractor

and Fig. 24.16b to a repeller.

One of the mathematical models often used to study the increasing of the population

leads to the quadratic logistic equation

−−

=− =

(1 ), const

xax x a ,

(24.1.107)

the fixed point being

∗

=−11/xa; we notice that =−() (1 )fx ax x, so that

∗

′

=−()2fx a

. Hence, for <<13a the fixed point is an attractor (Fig. 24.17a). For

= 3a it results a bifurcation which leads to a cycle of period 2 (Fig. 24.17b), which is

stable for

<<+316a . If a increases, then will result cycles of periods 4

(Fig. 24.17c),

8,16,...,2 ,...

Finally, if a increases very much, then one obtains a

chaotic regime, in which the trajectories are as thus corresponding to an aleatory

process (Fig. 24.17d).

24.2 Elements of the Theory of Catastrophes

From the oldest times, one of the basic wishes of men has to understand the intimate

mechanisms of the motion, of the change and of the permanent development, hence of

the evolution of the systems which surround us. After modelling the world on the basis

of faith in gods or starting from the observations on the motion of stars, men arrived to

scientific models of the evolution, models which have been continuously perfected. The

first models have had a deterministic character, e.g., the determinism of Newtonian

mechanics, representing thus a great achievement in the knowledge of the evolution of

phenomena of the nature. But, besides the phenomena with a continuous character, one

must mention the phenomena with a discontinuous or aleatory character too, which – as

a matter of fact – are much more numerous and the knowledge and understanding of

which is more and more important.

In this order of ideas, at the beginning of the eighth decade of twentieth century,

there have been set up new theories concerning the evolution of systems, i.e.: the theory

of dissipative systems (Prigogine, 1971), the synergetics (Haken, 1971) and the theory

of catastrophes (Thom, 1972). The theory of dissipative systems deals with the

behaviour of the system in the vicinity of the equilibrium or far from it, putting in

evidence the differences of state between the two states (Prigogine, I., 1980). The

synergetics studies, especially, the causes which produce the changes of phase, showing

why some of the variables lead to such changes, while other ones not (Haken. H.,

1982). The mathematical support of these two theories is given by the theory of

catastrophes, which shows how the phase transitions take place, of how many kinds

they are and of how many parameters they are influenced. Unlike the first two theories,

which have a qualitative character, the latter one is – essentially – quantitative. In fact,

the three theories are completing themselves.

Putting an accent on the qualitative transformations produced by jumps, which –

obviously – are discontinuous, René Thom elaborates the mathematical model of

evolutive processes (Thom, R., 1972). The corresponding theory is – one can say – a

mathematical theory of singularities, representing a true revolution in the differential

topology.

Dynamical Systems. Catastrophes and Chaos

683

In this order of ideas, we will present – in what follows – phenomena known as

ramifications and then we will pass in review the elementary catastrophes (Gilmore, R.,

1981; Gioncu, V., 2005; Poston, T. and Stewart, I., 1978; Zeeman, E. C., 1981).

24.2.1 Ramifications

The differential equation which models the behaviour of a differential system can

depend on one or on several parameters; for some values of these parameters can

After some general considerations, we present various types of ramification: fold,

fork, hysteresis, multiply ramification, generic ramification etc.

24.2.1.1 General Considerations

Let be the differential equation

=∈xxx(, ),

f λ



 ,

(24.2.1)

where

λ is a real parameter ∈λ  ; we can consider also the situation in which f

depends on an arbitrary number of parameters

, ,...,

λλ λ. Obviously, the critical

points are specified by the equation

=x(, ) 0f λ

(24.2.1')

A study of this nature has been made in Sect. 7.2.3.4, after Poincaré, for the positions of

equilibrium of a particle which moves according to the law

= (, )qfqλ , where q is a

generalized co-ordinate, obtaining a two-dimensional diagram, function of the

parameter

λ . To can use further such a diagram, assuming the existence of only one

parameter

λ , one introduces a representative scalar quantity x[] for the n -dimensional

vector

x , which can be: one of the components of the vector, eventually the most

important one

=x[]

x , the greatest component in absolute value

[ ] max{| |,| |,...,| |}

xx x=x or the Euclidean norm =xx[] | |. Obviously, each

of these choices for

x[] can give only partial informations about the phenomena to

study. In the case of differential equations with periodic solutions we can choose the

amplitude or the frequency for

x[].

Let us consider the graphic of the function implicitly definite in the form

=x([ ], ) 0f λ ,

(24.2.1'')

the smooth curves which are put in evidence being called branches. The particular solution

([ ], )λ of the equation (24.2.1'') for which the number of solution changes when λ

passes through

λ is called ramification point with respect to the parameter λ . For

appear what are called ramifications, the simplest one being the bifurcation (Chow, S.N.

and Hale, J.K., 1982; Hale, J.K. and Koçak, H., 1991; Iooss, G. and Joseph, D.D.,

1980; Seydel, R., 1988; Wiggins, S., 1988).

MECHANICAL SYSTEMS, CLASSICAL MODELS

684

instance, in the situation in Fig. 24.18) we have six ramification points

, 1,2,...,6

iλ = ,

resulting: one solution for

λλ

and

λλ

; two solutions for

≤<

λλλ

λλ

; three solutions for

, λλλλ==

,λλλλ

; and four solutions for

λλλ

Fig. 24.18 Ramification points of the equation (24.2.1'')

The ramifications can be simple ramifications: the fold, the fork (supercritic,

subcritic or transcritic), the hysteresis or the multiple ramifications.

If the equation (24.2.1') has real roots only for discrete real values of the parameter

λ , then the respective points are called isolated critical points. For instance, the

differential equation

=+ ∈

,xxxλ,

(24.2.2)

leads to

0xλ ,

(24.2.2')

having only the real root

= 0λ for which = 0x ; hence, the origin O is an isolated

critical point.

We say that a ramification is structurally stable if, introducing a small perturbation

of the form

+ xαβ, with α and β small parameters (one of which can vanish), that

one preserves its structural properties. In the case of the isolated critical point of the

equation (24.2.2'), introducing the mentioned perturbation, we may write

(

)

+++−=

αα

λβ

(24.2.2'')

/4βα , then the equation (24.2.2'') represents a circle with the centre at the point

/2, 0x αλ=− = and of radius −

/4αβ; if =

/4βα , then the circle is

reduced to its centre, at which is shifted the isolated point, while if

/4βα the

isolated point disappears. Hence, the isolated point is structural instable.

Dynamical Systems. Catastrophes and Chaos

685

If, after the perturbation by the mentioned linear term, the connection between the

branches and the point of ramification, with small displacements and eventual

deformations, are maintained, then the ramification is called generic ramification.

24.2.1.2 Fold

The simple ramification corresponding to the differential equation

=− ∈

,xxxλ,

(24.2.3)

is called fold (cuspidal point), the critical points being given by the algebraic equation

=− =

() 0fx xλ .

(24.2.3')

There result the real roots

0, xλλ≥=±, hence the diagram of ramification

(Fig. 24.19a), having two branches which meet at the point

′

O of ramification. We

notice that

′

=−() 2

fx x, so that

′

±=()2f λλ∓

; the branch =x λ is stable,

being represented by a continuous line, while the branch

=−x λ is instable and is

represented by a broken line.

Fig. 24.19 Fold: diagram of ramification (a); initial (broken line)

and perturbed (continuous line) fold (b)

Perturbing the equation (24.2.3') by a linear term, we obtain

(

)

⎛⎞

++ − − =

⎜⎟

⎝⎠

αα

λβ ,

(24.2.3'')

hence the same fold, with the point of ramification at

′

(−−

/4, /2βα α ); the

initial fold has been drawn by a broken line, while the perturbed one by a continuous

line in Fig. 24.19b. Hence, the fold is a structural stable ramification.

MECHANICAL SYSTEMS, CLASSICAL MODELS

686

We mention that the point of ramification of a fold does not always separate the

stable branch of the instable one.

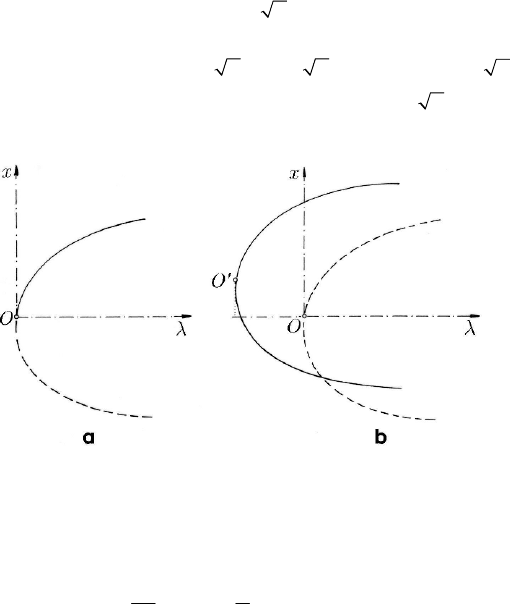
24.2.1.3 Fork

To the differential equation

, xxxxλ=+ ∈,

(24.2.4)

corresponds the equation

=+=

() 0fx x xλ ,

(24.2.4')

obtaining the branches

= 0x and =± −x λ for < 0λ ; the values of the derivative

′

() 3fx xλ lead to the representation in Fig. 24.20a. We maintain the continuous

line for the stable branches and the broken one for the instable branches. The above

ramification is called subcritical fork.

Fig. 24.20 Fork: subcritical (a); supercritical (b)

In case of the differential equation

, xxxxλ=− ∈,

(24.2.5)

the equation

−=

0xxλ

(24.2.5')

leads to

= 0x and =±x λ for > 0λ ; analogously, we get the ramification

diagram in Fig. 24.20b for the supercritical fork.

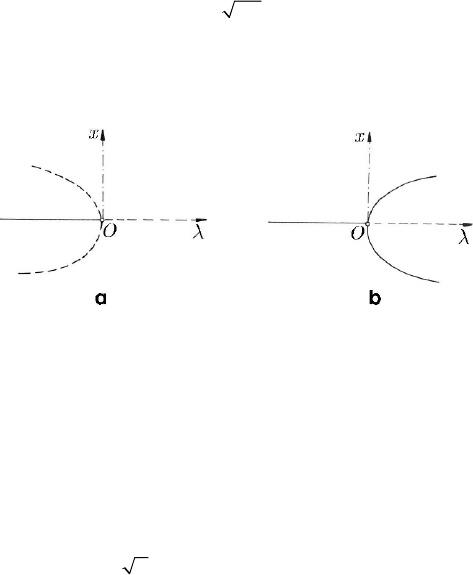
Let be also the differential equation

, xxxxλ=− ∈;

(24.2.6)

the critical points are given by the equation

−=

0xxλ ,

(24.2.6')

Dynamical Systems. Catastrophes and Chaos

687

obtaining the branches

= 0x and =x λ . This case is called transcritical fork,

corresponding the ramification diagram in Fig. 24.21.

In this case one can make a study of structural stability too. For instance, in the case

of a subcritical fork, adding a small parameter, we can write

Fig. 24.21 Transcritical fork

++=

0xxλβ.

(24.2.4'')

Representing, further, the non-perturbed ramification by a broken line and the perturbed

ramification by a continuous line, we obtain the diagram in Fig. 24.22a for

> 0β and

the diagram in Fig. 24.22b for

< 0β

. Hence, the subcritical fork ramification is

structurally instable, because new connections of branches are obtained.

Fig. 24.22 Subcritical fork ramification: 0β > (a); 0β < (b)

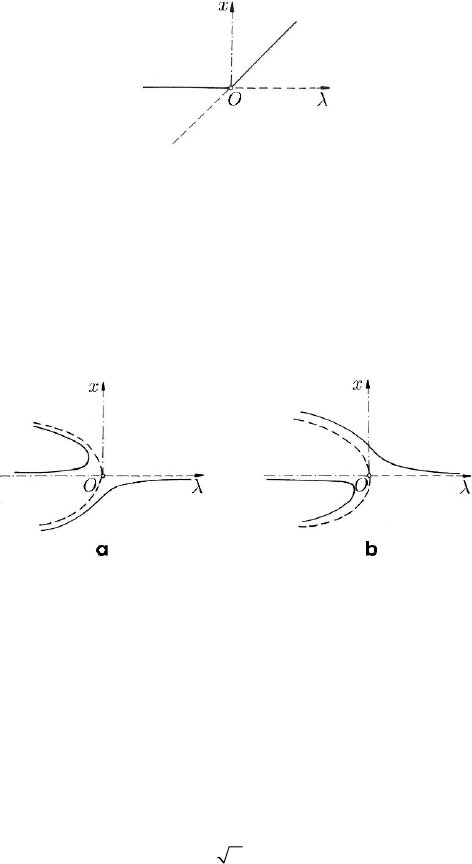
24.2.1.4 Hysteresis

For the differential equation

, xxxλ=− ∈

(24.2.7) ,

the critical points are given by the algebraic equation

−=

0xλ ;

(24.2.7')

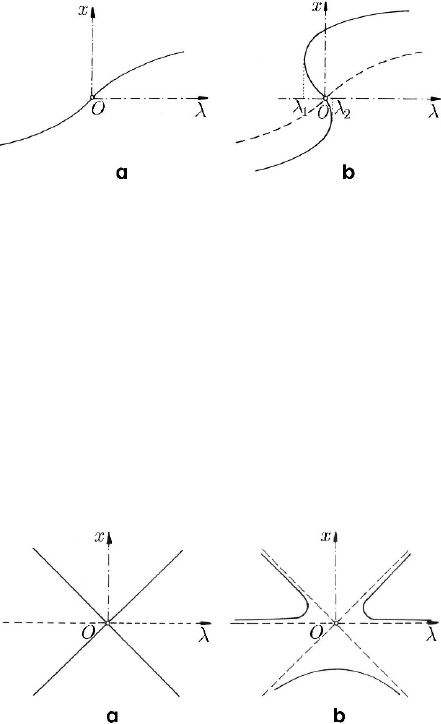
this equation has only one real root

x λ , both branches being stable (Fig. 24.23a).

The ramification is called hysteresis.

Introducing a perturbation

,xααsmall parameter, one can write

−+ =

0xx xλα

;

(24.2.7'')

MECHANICAL SYSTEMS, CLASSICAL MODELS

688

we obtain thus three real roots on the interval (

,λλ) and, with the same graphic

notations, the diagrams in Fig. 24.23b. Hence, the hysteresis is a structurally instable

ramification too.

Fig. 24.23 Initial (a); perturbed (b) hysteresis

24.2.1.5 Multiple Ramification

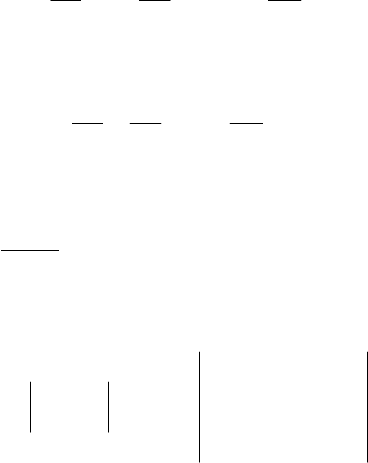
Another interesting differential equation is

, xxxxλ=− ∈;

(24.2.8)

the algebraic equation

−=

0xxλ

(24.2.8')

leads to the branches

= 0x , =±x λ . One obtains the branches in Fig. 24.24a, the

ramification point

O being a point of multiple ramification.

Fig. 24.24 Initial (a); perturbed (b) multiple ramification

Adding a perturbation of constant term

β (small parameter), we get the equation

−+=

0xxλβ

(24.2.8'')

With the usual graphic notations, we represent in Fig. 24.24b the non-perturbed and the

perturbed ramifications; hence, the multiple ramification is structurally instable.

Dynamical Systems. Catastrophes and Chaos

689

24.2.2 Elementary Catastrophes

After some general considerations concerning the critical points and the Morse

functions, one introduces, after René Thom, the notion of elementary catastrophe; one

presents then, in detail, the potentials of a single variable (the fold, the cusp, the

swallow tail and the butterfly) and the potentials in two variables (the elliptic umbilic,

the hyperbolic umbilic and the parabolic umbilic), corresponding to the elementary

catastrophes.

24.2.2.1 General Considerations

Let

( , ,..., )

fx x x be a function of n variables. The points

( , ,..., )

aa a at

which

∂∂ ∂

=+++ =

∂∂ ∂

d d d ... d 0

ff f

fx x x

xx x

are called stationary points or critical points; at these points

∂∂ ∂

====

∂∂ ∂

... 0

ff f

xx x

Let us denote

()

∂

∂∂

, ,..., , , 1,2,...,

aaaaijn

(24.2.9)

as well as

11 12 1

11 12 21 22 2

1112

21 22

, ,...,

aa a

aa a a a

aa a

Δ= Δ= Δ=

…

… ………

…

;

(24.2.9')

Δ> =0, 1,2,...,

in,

(24.2.9'')

then the stationary point corresponds to a minimum, while if

0, 1,2,...,

in(−1) Δ > = ,

(24.2.9''')

then the point corresponds to a maximum.

In the particular case

= 2n , the points ( ,ab) in which (,)/fab x∂∂

(,)/ 0fab y=∂ ∂ = are stationary points for the function (,)fxy; we denote

MECHANICAL SYSTEMS, CLASSICAL MODELS

690

∂∂ ∂

⎡

⎤

Δ= −

⎢

⎥

∂∂

⎣

⎦

22 2

(,) (,) (,)fab fab fab

(24.2.10)

Δ<0 , then will correspond a saddle point, while if Δ>0, then we have a local

extremum (a minimum if

∂∂>

(,)/ 0fab x or a maximum if ∂∂<

(,)/ 0fab x ); if

Δ=0 , then we cannot say anything from this point of view.

If the determinant of Hesse (the Hessian)

, definite by (24.2.9'), is non-zero, then

the differential

ddd

fxx

∂

∂∂

∑∑

(24.2.11)

is degenerate at the critical points; in this case, the function

( , ,..., )

fx x x is called a

Morse function.

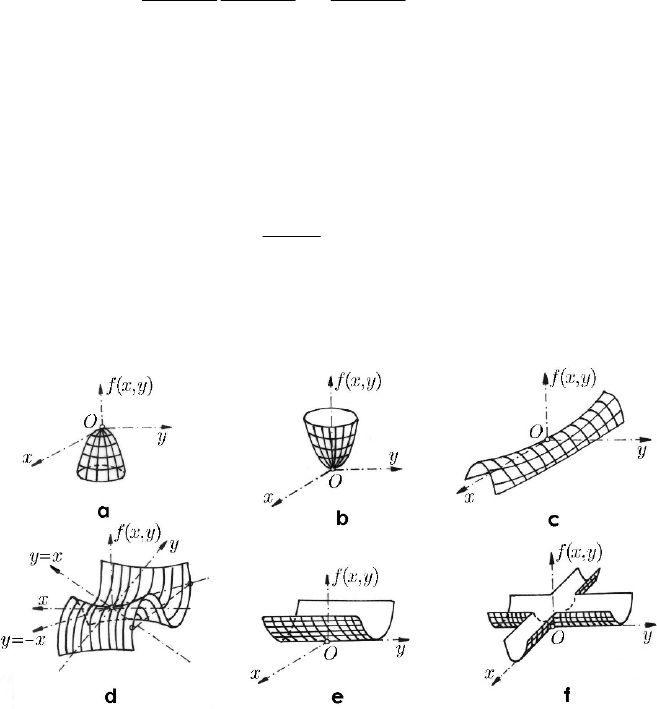
Fig. 24.25 Critical points of functions of two variables: maximum (a); minimum (b);

saddle (c); monkey saddle (d); channel (e); crossing channels (f)

We consider now some functions of two variables for which the origin is a critical

point. Thus, for

=− +

(,) ( )fxy x y the origin is a maximum (Fig. 24.25a), for the

function

(,)fxy x y the origin is a minimum (Fig. 24.25b), while for the

function

=−

(,)fxy x y the origin is a saddle point (Fig. 24.25c); the Hessian being

non-zero, these functions are Morse functions. For the function

=−

(,) 3fxy x xy

the origin is a monkey saddle point (Fig. 24.25d), for the function

(,)fxy x

the

origin is a channel point (Fig. 24.25e), while for the function

(,)fxy xy the origin

is a crossing channels point (Fig. 24.25f); these functions are not Morse functions. The

critical points of the first four functions are isolated critical points.

Dynamical Systems. Catastrophes and Chaos

691

Adding a small linear perturbation, on can show that a Morse function is structurally

stable. One can easy see that the function

()fx x is structurally stable, the functions

() , 3

fx x n=≥, being structurally instable; in this last case, one can add terms of a

smaller degree to obtain a structurally stable function. We notice that, in a polynomial

−−

−

+++++

12 1

...

nn n

ax ax ax a x a , by two substitutions – which represent

two translations from a structural point of view – we can make to disappear the term

−1

ax and the free term

a ; thus, after

x we add only terms beginning with

−2

and without any constant.

One obtains thus – after René Thom – elementary catastrophes in one variable;

analogously, one can introduce elementary catastrophes in two variables. The

corresponding functions, called potentials, will be of the form

( ; , ,...)Vxab or

( , ; , ,...)Vxyab , where , ,...ab are parameters. Eliminating x between the equations

which specify the singularities

∂∂=/0Vx (which we represent in the phase space)

and

∂∂=

/0Vx or eliminating x and

between ∂∂=∂∂=//0Vx Vy and

22222 2

(/)(/)(/ )0Vx Vy Vxy∂∂∂∂−∂∂∂=

, one obtains a relation of the form

=( , ,...) 0fab ,

(24.2.12)

which represents a surface in the control space of the parameters

,,...ab

One can thus

appreciate the number of possible positions of equilibrium of the considered dynamical

system, as well as their stability.

24.2.2.2 Elementary Catastrophes in One Variable

The most simple elementary catastrophe is the fold, the potential of which is

=+ =

() , const

Vx x axa

;

(24.2.13)

Fig. 24.26 Representation of the potential of a fold: phase space (a); control space (b)

the first two derivatives are

=+ =

xa x

(24.2.13')

We deduce the equations