Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

692

0, 2 0xa x+= =.

(24.2.13'')

The first equation represents a parabola in the phase space, for

< 0a (Fig. 24.26a); by

eliminating the variable

x , we obtain = 0a in the control space (Fig. 24.26b). In

conclusion, for

> 0a we have no position of equilibrium, for < 0a we have two

positions of equilibrium: one stable

=−xa (for which

=−>

d/d 2 0Vx a

)

and one instable

=− −xa(for which =− − <

d/d 2 0Vx a ), while for = 0a

we have a double root

= 0x , to which corresponds a cuspidal point.

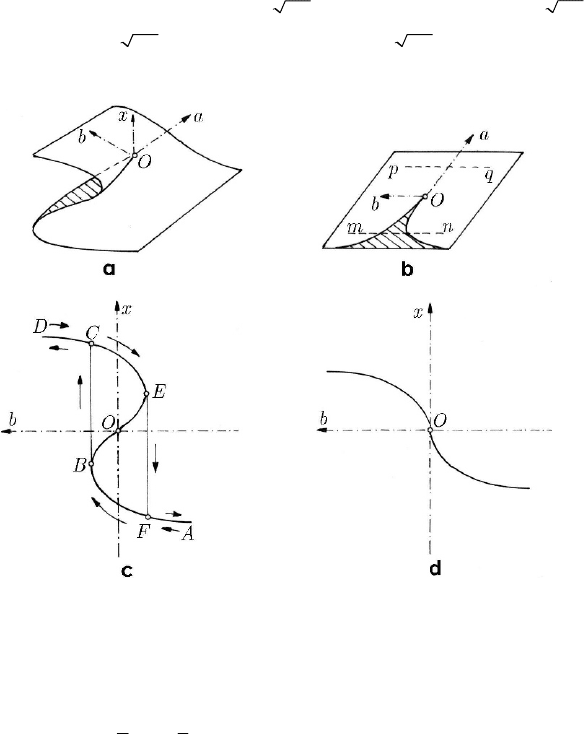
Fig. 24.27 Representation of the potential of a cusp in the control space: the surface S (a); the

semi-cubical parabola (b); section by a plane

consta = ; 0a < (c); 0a > (d)

An elementary catastrophe of fourth degree is the cusp of potential

=+ + =

() , , const

Vx x ax bxab

;

(24.2.14)

its derivatives allow to write the equations

++= +=

0, 3 0xaxb xa .

(24.2.14')

The first equation leads, in the phase space, to the surface

S in Fig. 24.27a. By

eliminating the variable

x between the equations (24.2.14'), we obtain the equation

4270ab,

(24.2.14'')

Dynamical Systems. Catastrophes and Chaos

693

corresponding to a semi-cubical parabola (the cusp)

3/2

(), 0

baa=± − <

(24.2.14''')

symmetric with respect to the

Oa -axis (Fig. 24.27b). If the point (,)ab belongs to the

hatched domain, then the first equation (24.2.14') has three real roots, while if it is

outside that zone, then it has only one real root; finally, if the point

(,)ab is on the

cusp, then the equation has all the roots real (one simple and one double).

A section by a plane

const, 0aa=<, parallel the plane to Oxb , pierces the

surface

S along the curve in Fig.24.27c; hence, the trace of the plane Oab is mn . If

we start from

A and b is increasing, one travels through the path ABCD , having a

jump

BC ; starting from D , with b decreasing, the path DEFA with the jump EF is

travelled through. Hence, the branch

BOE is instable. If > 0a , then the trace on the

plane

Oab is pq , the intersection with the surface S being the curve in Fig.24.27d.

Fig. 24.28 Representation of the potential of a swallow tail in the control space

The potential of fifth degree

=+ + + =

532

11 1

() , ,, const

53 2

Vx x ax bx cxabc

(24.2.15)

corresponds to the elementary catastrophe called swallow tail. The equations

+++= ++=

42 3

0, 4 2 0aaxbxc x axb

(24.2.15')

put in evidence the position of equilibrium and the critical points, respectively. By

eliminating the variable

x , one obtains a relation of the form =(,,) 0fabc . which

represents a surface

S in the control space. To make a study of this surface, we

calculate

MECHANICAL SYSTEMS, CLASSICAL MODELS

694

()

=− + = +

ddc

12 2 , 12 2

xa xax

wherefrom

=−d/dcb x. One obtains the representation in Fig. 24.28 of the surface

S , which has four critical points: the point of maximum O , the cuspidal points A and

B and the point of self-intersection C ; the name given to this elementary catastrophe

is justified by the form of the cross section for

< 0a .

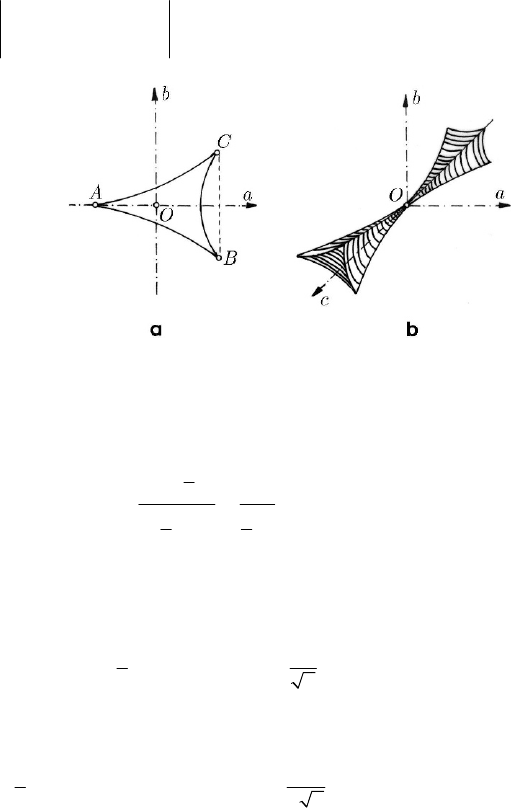
The potential of sixth degree

=+ + + + =

6432

11 1 1

() , ,,, const

64 3 2

Vx x ax bx cx dxabcd

(24.2.16)

corresponds to the elementary catastrophe called butterfly. One obtains the equations

532 4 2

0, 5 3 2 0x ax bx cxd x ax bxc++++= + ++=;

(24.2.16')

in this case, the phase space is five-dimensional, while the control space is

four-dimensional. To can make a study of the hypersurface

=(,,,) 0f abcd in the

control space, we start from

=− − − = + +

42 532

() 5 3 2 , () 4 2cx x ax bx dx x ax bx .

For instance, for

= 0b and for the butterfly factor < 0a , one obtains the

representation in Fig. 24.29, which justifies the denomination of butterfly given to this

elementary catastrophe. The points

A and

have the co-ordinates =

(9/20)ca and

=−

(6/25) (3/10)daa∓

, respectively, the points D and E have the co-ordinates

= 0c and =± −

(6/25) (3/5)daa, respectively, while the point of

self-intersection

C has the co-ordinates =

(1/4)ca and = 0d . Obviously, one can

build up also other curves, corresponding to other values of

a and b .

Fig. 24.29 Representation of the potential of a butterfly in the

control space for 0b = and 0a <

One can consider also potentials of higher degree, but which are less useful in

practical applications.

Dynamical Systems. Catastrophes and Chaos

695

24.2.2.3 Elementary Catastrophes in Two Variables

The most important elementary catastrophe in two variables is the umbilic. Thus, the

potential

()

=− +++ + =

32 22

(,) , ,, constVxy x xy ax by cx y abc

(24.2.17)

leads to the elliptic umbilic. The phase space and the critical points are given by the

equations

()

−++ =− ++ =

+−

=− + − − =

−−+

22 2

320,220,

62 2

43 2 0.

222

xyacx xybcy

xc y

xy cxc

yxc

(24.2.17')

Fig. 24.30 Representation of the potential of an elliptic umbilic in the

control space (a); a section

constc = (b)

We notice that the last of these equations can be written also in the form

()

−

(24.2.18)

the denomination of this elementary catastrophe being thus justified.

We can use the parametric representation

=+ =

(1 2 cos ), sin

xc y cθθ;

(24.2.18')

the first two equations (24.2.17') lead then to

=− + + = −

(3 8 cos 4 cos 2 ), (sin 2 2 sin )

ac b cθθ θθ

(24.2.18'')

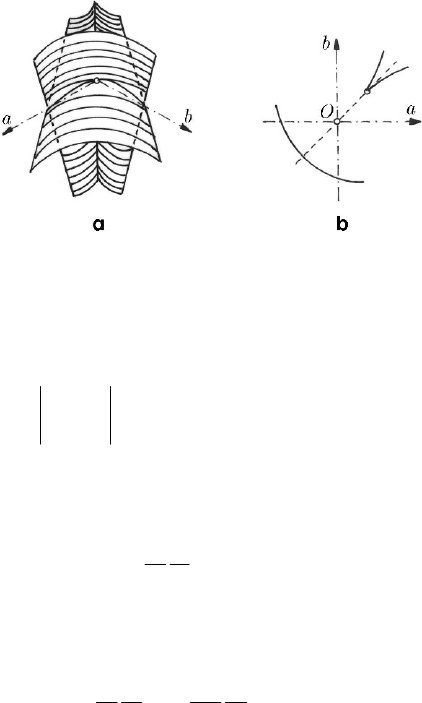
MECHANICAL SYSTEMS, CLASSICAL MODELS

696

The surface is reduced to the point

==0ab for = 0c . The sections made in the

surface

=(,,) 0fabc by the plane = constc have three cuspidal points for = 0θ

and

=±2/3θπ; to these values of the parameter θ correspond the points

−−

222

(5 ,0), ( ,2 )Aa Bc c and

(,2)Cc c . The plane Oab is a plane of symmetry for

the surface in the control space, because the co-ordinates of these points remain the

same if one replaces

c by −c . This surface is drawn in Fig. 24.30a, while in

Fig. 24.30b is drawn a section

= constc in it.

The hyperbolic umbilic has the potential

=+−−+ =

(,) , ,, constVxy x y ax by cxyabc .

(24.2.19)

Fig. 24.31 Representation of the potential of an hyperbolic umbilic in the

control space (a); a section

constc = (b)

The equations

30,30,

36 0

xaxcy ybcx

xy c

−+= −+=

=−=

(24.2.19')

specify the five-dimensional phase space and the critical points; the control space

three-dimensional. The last of these equations can be written in thus form

(24.2. 20)

too, which justifies the name given to this elementary catastrophe; choosing

x as a

parameter, we also find

=+ = +

36 432

ax b cx

(24.2.20')

Proceeding analogously, we make sections by planes

= constc . If = 0c , then

==0ab ; hence, the axes Oa and Ob belong to this surface. In Fig. 24.31a one

presents the surface

S , while in Fig. 24.31b is given a section by a plane = constc .

Dynamical Systems. Catastrophes and Chaos

697

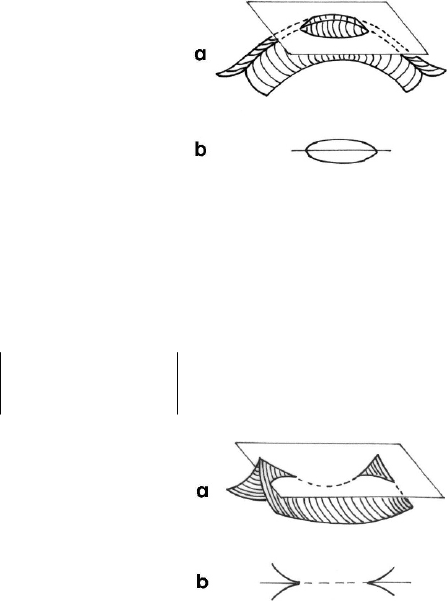
The potential

=+ +++ + =

42 2 2

(,) , ,,, constV x y y x y ax by cx dy a b c d ,

(24.2.21)

Fig. 24.32 Representation of the potential of a parabolic umbilic in the

control space: lips (a); plane sections (b)

corresponds to a parabolic umbilic for which the six-dimensional phase space and the

critical points are specified by the equations

()

32 2

220,4 20,

22 2

46 6 0.

2122

xy a cx y x b dy

yc x

ycydyxcd

xyd

++ = + ++ =

=++−+=

(24.2.21')

Fig. 24.33 Representation of the potential of a parabolic umbilic in the

control space: beak to beak (a); plane sections (b)

Eliminating

x and y , we obtain the surface =(,,,) 0f abcd in the four-dimensional

control space. Assuming that the coefficients

c and d have constant values, one

obtains figures characteristic also for other catastrophes, but also other figures, i.e.: lips

(Fig. 24.32a), which leads to the curves in Fig. 24.32b, as well as beak to beak

(Fig. 24.33a), which leads to the curves in Fig. 24.33b.

24.3 Periodic Solutions. Global Bifurcations

In what follows, we treat also other interesting aspects concerning the differential

equations: periodic solutions and global bifurcations; obviously, we will take in

evidence the stability problems which are put.

MECHANICAL SYSTEMS, CLASSICAL MODELS

698

24.3.1 Periodic Solutions

We have defined, in Sect. 24.1.1.1, the periodic solutions, in the general case of

non-autonomous differential systems. We shall consider now only autonomous systems

of the form

=∈xfxx(),

 ,

(24.3.1)

for which the solution

==xxI

() () , ()tt tΦΦ ,

(24.3.1')

called periodic solution, has the property

+= ∀∈()(),tT t t ΦΦ .

(24.3.1'')

The motion is repeated after intervals of time

, nT n ∈ 

; we call period the smallest

interval of time

T after which the motion is repeated. After some considerations with a

general character, one introduces the Hopf bifurcation, which allows to generate some

periodic solutions; one presents then the Lindstedt method of integration and one makes

a study of stability of the periodic solutions.

24.3.1.1 General Considerations

In the phase space, the image of the periodic motion specified by the equation

(24.3.1) is a closed curve (orbit or cycle). In the case of an autonomous system of

differential equations, to a closed orbit without critical points – in the phase space –

corresponds always a periodic solution; if the system of differential equations is a

non-autonomous one, then this property does no more hold.

The study of the periodic motions plays an important rôle due to the fact that many

phenomena in the nature have such properties; even in the case of a chaotic behaviour

can appear such periodic motions, in certain conditions. On the other hand, as we have

seen in §1, the periodic motions separate the stable configurations of a dynamical

system from the instable ones.

In particular, let be the two-dimensional system

1 112 2 212

(, ), (, )xfxxxfxx,

(24.3.2)

definite in a simply connected domain

⊂

D , the functions

and

being of class

C . If C is the cycle corresponding to a periodic solution, then we can write

()( )

12 21 12 21 12

dd d d d d 0

DCC

xx fx fx xx xx

∂∂

⎛⎞

+=−+=−+=

⎜⎟

∂∂

⎝⎠

∫∫ ∫ ∫





;

hence, the expression

∂∂+∂∂

11 22

//fx fx cannot maintain a constant sign in the

interior of the domain

D . We can thus state Bendixon’s criterion: The system of

Dynamical Systems. Catastrophes and Chaos

699

differential equations (24.3.2) admits periodic solutions only if the expression

∂∂+∂∂

11 22

//fx fx changes its sign or equates zero.

Let us consider, e.g., Van der Pol’s differential equation

()

−− +=

10xxxxμ  ,

(24.3.3)

equivalent to the linear system

()

==−+−

122 1 12

,1xxx x xxμ ;

(24.3.3')

we calculate the expression

()

∂∂

+=−

∂∂

μ ,

(24.3.3'')

which vanishes for

=±1x

. Hence, the equation does not admit a periodic solution

situated entirely in the half-space

<−1x or in the half-space > 1x or in the strip

−< <11x ; if it has a periodic solution, then this one will intercept one of the straight

lines

=±1x or both of them.

Bendixon’s theorem 23.1.22 (called, sometimes, the Poincaré–Bendixon theorem

too) ensures the existence of a closed trajectory, hence of a periodic solution in the

phase space.

Let us tackle again the system of differential equations (23.1.77), considered in Sect.

23.1.2.7, for which the origin

0xx is the only critical point; the linearized

system is

=− =+

12 1 2

Rx x x Rx

ωω,

(24.3.4)

with the characteristic equation

−−

=− ++=

−

2242

λω

λλ ω

ωλ

of roots

=±

1,2

iRλω. The critical point is thus an instable focus. We calculate now

the scalar product of the vector

(, )xx and v

(, )xx, which make the angle α , in

the form

()( )

⋅= = + = + − −rv rv

22 222

11 22 1 2 1 2

cos xx xx x x R x xα  .

Let us consider the circles of radii

r and

r and the circular annulus for which

and

rR; along the circumference of radius

r one has

⋅rv

22 2

11 1 1

cos ( ) 0rv r R rα==−>, hence cos 0, 0 /2ααπ><<, while along

MECHANICAL SYSTEMS, CLASSICAL MODELS

700

the circumference of radius

r one has ⋅= = − <rv

22 2

22 22 2 2

cos ( ) 0rv r R rα , hence

cos 0, / 2απαπ<<<, so that the trajectories enter inside the circular annulus.

Hence, the circular annulus is a bounded domain which does not contain critical points

of the system of differential equations, and the trajectories ones entered in this domain,

remain there; according to the Poincarè–Bendixon theorem, the system of differential

equations (23.1.77) admits at least a closed trajectory entirely situated in the interior of

the circular annulus, hence at least a periodic solution of the form

=−=−

cos( ), sin( )xR t xR tωϕ ωϕ,

(24.3.4')

as it can be easily shown.

Let be Liénard’s differential equation

++=() 0xfxxx  ;

(24.3.5)

one can show that this equation admits a periodic solution if:

(i) the function

()fx is Lipschitz continuous in  ;

(ii)

∫

() ()d

Fx fξξ is an odd function;

(iii) there exists a constant

> 0α so that, for <<0 x α , one has <() 0Fx ;

(iv) there exists a constant

> 0β so that, for >x β , >() 0Fx is monotone

increasing and

→∞

=∞lim ( )

Fx .

As well, the differential equation

+=() 0xfx

(24.3.6)

admits a periodic solution if

()fx is an odd function of class

C , definite in



, which

verifies the condition

>() 0fx for 0, 0x αα<≤ >.

Fig. 24.34 The system of differential equations (24.3.7); the diagram (, ) 0

r λ =

Let be the system of differential equations (24.2.1), depending on the real parameter

∈λ  ; a study of the equation has been made in Sect. 24.2.1.1, obtaining a statistical

ramification diagram and a certain number of configurations of equilibrium. We notice

that, for certain values of the parameter

λ , it is possible to have not such a motion; in

this case too, one can build up a diagram of ramifications, there appear points of

ramification etc.

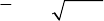
Dynamical Systems. Catastrophes and Chaos

701

Let be, e.g., the system of differential equations in polar co-ordinates, in

 ,

===

(, ), , constrfrλθ ωω



;

(24.3.7)

the diagram

=(, ) 0frλ which – obviously – corresponds to some circular periodic

motions with the angular velocity

ωω, can have the form in Fig. 24.34. In this

case, for

, , λλλλλλ=== there exists a periodic motion, for <

λλ,

234

, λλλλλλ<< << there exist two periodic motions, for

, λλλλ==

there exist three periodic motions, while for

λλλ

there exist four periodic

motions; for

λλλ and >

λλ there do not exist periodic motions.

Sometimes, it is quite difficult to get the number of the periodic solutions.

24.3.1.2 Hopf’s Bifurcation

The local bifurcations govern, in general, the mutation of the configurations of

equilibrium or of the limit cycles. We mention thus Hopf’s bifurcation, which

transforms a configuration of equilibrium into a limit cycle (Marsden, J.E. and

McCracken, M., 1950).

Let be a damped non-linear free oscillator, the motion of which is described by the

differential equation

++ + =

(,) 0xkx xfxxω   ,

(24.3.8)

where

(,)fxx contains the non-linear terms; the equivalent system of differential

equations is of the form

==−−−

122 2 1 12

,(,)xxx kx xfxxω .

(24.3.8')

It is easily seen that to a change of sign of the constant

k , from + to –, the eigenvalues

of the linearized system pierce the imaginary axis at

,λλ ω=± −

. Hence, the Hopf

bifurcation can be associated with the vanishing of the linear damping in the motion of

an oscillator.

Let us consider also the Van der Pol equation

()

10, 0xx xxαωα+−+=> 

(24.3.9)

which represents the motion of a non-linear oscillator after a Hopf bifurcation. If

x is

small, then we can neglect the term

in the bracket, obtaining an oscillation of

increasing amplitude. If

x increases, then the term of linear damping

xx becomes

dominant, but the motion must remain bounded. In the phase portrait, the system leads

to a postcritic limit cycle.

One obtains the same conclusion using the term

()fx x

, which corresponds to

the equation