Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

722

A. Douady showed that one can obtain a great number of Julia sets: “Some of them

appear as thick clouds, other ones as a dry thorn, other – further – as sparks winding as

fireworks; someones seem to be as a hare, while many of them have a tail as a sea

horse”.

Fig. 24.51 Barnsley’s fern, obtained using Hutchinson’s operator

The Mandelbrot set generalized the Julia set; the latter one is in the plane of the

initial values

z , but the Mandelbrot set belongs to the plane of the complex constant

c . An image of this set is given in Fig. 24.52; one may notice a great complexity: an

interior without any structure and frontier with an infinity of various forms with a

fractal structure, of fractal dimension close to

2 . It seems that this fractal is one of the

most beautiful and complex objects of modern mathematics, leading to numerous

researches.

Fig. 24.52 An image of the Mandelbrot set

Dynamical Systems. Catastrophes and Chaos

723

24.4.2 Chaotic Motions

After some introductory considerations and some elements of the theory of signals,

Lyapunov’s exponents and Mel’nikov’s method are presented. A special attention is

given to the strange attractors and to the evolution towards chaos. As examples, one

makes a study of Duffing’s and of Van der Pol’s equation. As well, the mappings of

Feigenbaum and of Hénon are put in evidence.

24.4.2.1 Introductory Considerations

It is very difficult to show what is regular and normal, ordered or chaotic. The notion

of “chaos” appeared long time ago by Anaxagoras (Vth century A.C.), but it became

various forms, various modes to be understood along the time.

If e.g., the sequence of natural numbers

1,2, 3,... or the rational ones (e.g.,

2/ 3 0.666...= ) present a certain regularity, then the irrational numbers (e.g.,

2 1.4142135...= ) or the transcendent numbers (e.g., 3.1415926...π = ,

e 2.7182818...= ) have not any regularity; the Champernowne number

0.123456789101112...C = , formed by the succession of the natural numbers put after

the point, hence after a certain rule, is a transcendent number too.

Even if the chaotic motions have been discovered by Poincaré, a profound

knowledge in this direction has been obtained together with the apparition of the

electronic computers. In the last 50 years, one can mention the researches made by the

meteorologist Edward Lorenz in 1963, taken again by David Ruelle and Floris Takens

in 1971, who introduced the notion of strange attractor (after other researches, chaotic

attractor). Mitchell Feigenbaum showed that there exist chaotic phenomena interrupted

by periodical windows. Benoit Mandelbrot has introduced, as we have seen, the notion

of fractal, while Stephen Smale discovered, studying dynamical systems, a mapping

which, defined on a square, transforms this one, by stretching in a direction, by

contraction in the transverse direction and by folding – in a horseshoe, called Smale’s

horseshoe (Smale, S., 1980).

Fig. 24.53 Portrait of the motion in case of a deterministic chaos

We mention also that, in the study of motions depending on parameters, for certain

values of them, there can appear the phenomenon of chaos, which is – in this case – a

deterministic chaos.

To study chaotic phenomena, one must put in evidence a significant variable

()Zt ;

supposing that one can obtain the values of this variable at discrete intervals of time,

MECHANICAL SYSTEMS, CLASSICAL MODELS

724

denoting

( ) , 0,1,2,...

Zk Z kτ == If the dynamical system is deterministic, then we

can determine

( , ,..., )

kkkkr

ZZZZϕ

−− −

= , where we can have 1,2,...,rk= ; in the

most simple case

1r =

. Thus, a dynamical system can lead to a strange attractor.

()ZZt= corresponds to only one significant variable, then we can represent the

motion at a moment

t by a point (,)ZZ



in the phase plane, obtaining a portrait of the

motion for various values of

; thus, we obtain simultaneously both the position and the

velocity of a representative point.

In the case of a periodic motion, this portrait is a closed curve, while in the case of a

regular motion it is a curve which tends to a stable fixed point or to a limit cycle, In

case of a chaotic motion, one obtains a portrait with a complex aspect, e.g., as that in

Fig. 24.53.

Let be the points

((),())xt xt in the phase plane for 0, ,2 ,...t ττ= , the time

interval

τ being conveniently chosen, e. g., the period of a perturbing force which may

intervene in the system of differential equations of a dynamical system. The set of these

points constitutes the stroboscopic image of the motion of the dynamical system, hence

a Poincaré mapping; thus, a three-dimensional study is reduced to a two-dimensional

one.

Fig. 24.54 A Poincaré section corresponding to one of Ueda’s strange attractors

One obtains thus a Poincaré section. A periodic motion is thus reduced to a point,

subharmonic periodic motions to a finite number of points and a motion which tends to

a limit cycle to an infinite number of points which have as limit point the stroboscopic

image of the motion on this cycle. In the case of a chaotic motion, the Poincaré section

has a much more complex aspect, e. g., that in Fig. 24.54, corresponding to one of

Ueda’s strange attractors.

Let us try to study a deterministic chaotic system by means of a statistical system. If

the system is formed of

N elements, one of them being produced with a probability

, 1,2,...,

pi N= , then the entropy of the system is defined by the relation

Dynamical Systems. Catastrophes and Chaos

725

log

Spp

=−

∑

(24.4.18)

This quantity can be considered as a measure of “the quantity of information” or, for

the dynamical system, as a measure of “the quantity of disorder”. If the system is of

equal probability, then we have

1/pN= , so that

logSN=

, corresponding the

maximal entropy; if the probability is equal to the unity, then it vanishes for all the

other events (indeed, the sum of all the probabilities is equal to one), so that

0S = ,

attaining its minimal value.

24.4.2.2 Lyapunov’s Exponents. Mel’nikov’s Method

The divergence of the trajectories which start from very near initial positions leads,

usually, to chaotic motions.

Let be the equation

( ), , ( ; )xfxx xxtx=∈=, with the initial condition

(0; )xx x= . If tΔ is a sufficiently small interval of time, then let us denote

( ; ), 1,2,...,

xxktxk n=Δ = . A neighbouring motion starts from the point

, x δδ+ sufficiently small; let us denote

(, ) (,)xtx xtxδδ=Δ +−Δ .

(24.4.19)

If we express the relation between

δ and

δ in the form

δδ= ,

(24.4.19')

then the exponent

L can be chosen as a measure of the divergence between the two

trajectories. Starting from the initial positions

x and

x δ+ , we find, analogously,

21 1

(, ) (,) e

xtx xtxδδ δ=Δ +−Δ =

(24.4.20)

a.s.o.; in general,

(, ) (, ) e

xtx xtxδδ δ

−−

=Δ +−Δ = ,

(24.4.21)

wherefrom

= .

(24.4.21')

Taking the mean of the exponents thus introduced, till

, we obtain

n=1 n=1

LL l

∑∑

;

(24.4.22)

making

0δ → , we get

MECHANICAL SYSTEMS, CLASSICAL MODELS

726

d( ,)

∑

(24.4.23)

a useful formula if

tΔ is sufficiently small and if the order N of iteration is

sufficiently great. The number

L is a Lyapunov exponent.

If we have to do with a system of

1n > differential equations, then one calculates the

Lyapunov exponents

, ,...,

LL L, the most important of them being the greatest one; if

this exponent is positive, then the motion is chaotic. If the maximal Lyapunov exponent is

negative, then appear the so-called “periodic windows”. One can thus see that the Lyapunov

exponents play an important rôle in emphasizing the chaotic character of a motion.

It is known that the heteroclinic and homoclinic trajectories have an instable

character. A homoclinic trajectory is, at the same time, a stable and an instable variety

for the same critical point; as a consequence of a perturbation, these varieties do not

coincide any more, being distinct, These varieties can pierce each other, and if the

intersection is a transverse one – very complicated trajectories are generated, the motion

becoming chaotic. In connection with these problems one can mention the Lambda

theorem given by Palis in 1969, the theorems of Smale and Birkhoff, as well as Smale’s

horseshoe; V.K. Mel’nikov made studies in this direction too.

Let be a time periodic system of the form

() (;),tUε=+ ∈⊂





xfx gx x ,

(24.4.24)

where

()fx is a Hamiltonian vector field

112 212

(, ) ,(, )

fxx fxx

∂∂

==−

∂∂

while

ε is a small parameter.

We suppose that this system of two differential equations admits a homoclinic orbit,

for

0ε = , at a saddle point

P and that, for 0ε ≠ , it has a point P

with two distinct

varieties: a stable variety and an instable one. If

(, )

qtt

and

(, )

qtt

are the

positions of two points situated one the instable or on the stable variety of the critical

point

at the moment

tt= , respectively, then – by an expansion into a power series

– we can write

000 0 0

(, ) (, ) (, ) ( ), ( , ],

(, ) (, ) (, ) ( ), [ , ).

ss s

ii i

qtt qtt qtt t t

εε

=+ +∈−∞

=+ +∈∞

(24.4.25)

We notice that

00 00 0

(, ) (, ) (, )

qtt qtt qtt== corresponds to the same point on the

homoclinic trajectory.

Defining Mel’nikov’s function in the form

()( )

000

() (,) (,), dMt q tt q tt t t

∞

−∞

=∧

∫

fg ,

(24.4.26)

Dynamical Systems. Catastrophes and Chaos

727

we can state

Theorem 24.4.1 (Mel’nikov). If Mel’nikov’s function has simply zeros and is

independent on

ε , then – for 0ε > , sufficiently small – the instable variety and the

stable one have a transverse intersection. If

()Mt does not equate to zero, then these

varieties do not pierce one the other.

The possibility of apparition of chaotic motions in case of Hamiltonian systems

definite on a domain in

 is thus put in evidence.

24.4.2.3 Strange Attractors. Smale’s Horseshoe. Routes to Chaos

We have met, in the first paragraph of this chapter, the notion of simple attractor in

the form of stable fixed points, stable limit cycles or in the form of tori of various

orders.

The strange attractors (or chaotic attractors) are characterized by a fractal structure

or by a fractal structure of the frontier of the attractor’s basin and have a great

sensibility to the initial conditions; thus, it is very difficult to foresee a chaotic motion,

especially if the fractal dimension of the attractor is great. Using a conjecture stated by

James Kaplan and James Zorke in 1978, one can foresee the dimension of a strange

attractor, in some cases, if one knows Lyapunov’s exponents (Hénon, M. and

Pomeau, Y., 1976; Ruelle, D., 1989).

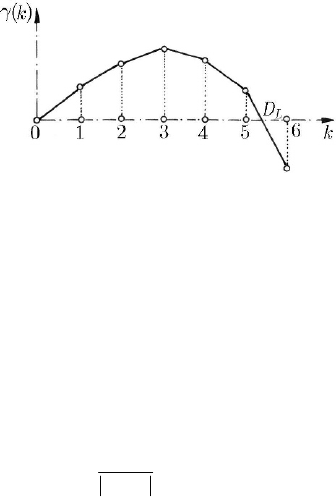
Fig. 24.55 The graphic of ()kγ vs k; Lyapunov’s dimension

One starts from the exponents

...

LL L≥≥≥ defining the function

( ) ... , , (0) 0

kLL Lknγγ=+++ ≤ =;

(24.4.27)

we draw the graphic of this function, assuming that between two successive natural

numbers (

k and 1k + ) one has a straight line (Fig. 24.55). Lyapunov’s dimension of

the strange attractor is given by

Dm L

∑

(24.4.28)

where

m is the greatest integer with () 0mγ ≥ ; if

0L < or 0

D = , then the

attractor is not a strange one.

MECHANICAL SYSTEMS, CLASSICAL MODELS

728

An important rôle in understanding the fractal structure of a strange attractor is

played by Smale’s horseshoe, introduced by the application

Fig. 24.56 Smale’s horseshoe: application f

()

{

}

:,,0,1fD D xy xy→= ∈≤≤;

(24.4.29)

Fig. 24.57 Smale’s horseshoe: application

−

the square has a contraction of

1/2λ < in the direction of the Ox -axis, a stretching of

2μ >

in the direction of the Oy -axis and then a folding (Fig. 24.56). The inverse

mapping

−

acts on the domain D by a stretching of 1/λ along the Ox -axis, a

contraction of

1/μ along the Oy -axis, followed by a folding (Fig. 24.57). The

application

()fD D∩ leads to two vertical rectangles (Fig. 24.58a) while the

application

()fD D

−

∩ leads to two horizontal rectangle (Fig. 24.58b).

Fig. 24.58 Smale’s horseshoe: two vertical (a) and horizontal (b) rectangles

Applying several times the mapping

f of Smale, one can define the mappings

, ,...,

ff f; analogously, starting from the inverse mapping

−

, we obtain the

mappings

, ,...,

ff f

−− −

. Applying the mapping

to the set

Dynamical Systems. Catastrophes and Chaos

729

()

AfD

∞

=−∞

∩

(24.4.30)

we see that ()fA A= , obtaining thus a strange attractor; there have thus been put in

evidence the character of self-similarity and that of fractal of “two-dimensional Cantor

set” type. The Hausdorff dimension of this attractor is equal to the double of the

dimension of a Cantor set, hence

2 log 2/ log 3 1.2618

D ==.

The operations corresponding to Smale’s operator

can be compared to those made

by a pastry cook when he is preparing a paste: a succession of contractions and

stretchings in two orthogonal directions, followed by a folding of it.

In general, we can consider a system of differential equations of the form

(,), ,

=∈∈





xfxax a ,

(24.4.31)

or the system of recurrence equations

(,), ,

−

=∈∈xfxax a .

(24.4.31')

The column vector parameter

[ , ,..., ]

aa a=a plays an important rôle; its

components can lead to a regular or to a chaotic behaviour of the system of equations.

Let be a system which depends on only one parameter

a . If the solutions of the

system have a regular (stationary, periodic or pseudoperiodic solutions) behaviour for

aa< and if the system begins to have a chaotic behaviour for

aa> , then one has

an evolution towards chaos for

aa= ; but, for

aa> , there can exist periodic

windows, usually narrow, for which the system has once more a regular behaviour.

One can identify three principal routes to chaos: (i) by three bifurcations (the

Ruelle-Takens theory); (ii) by doubling the period (Feigenbaum’s theory); (iii) by

intermittency (Devaney, R., 1986; Gutzwiller, M.C., 1990; Kapitaniak, T., 1990, 1991,

1998; Schuster, H.G., 1984).

Thus, in the first scenario, starting from a stationary state, a first bifurcation leads the

system to a periodic state, when appears only one pulsation

ω ; a second bifurcation

leads to a pseudoperiodic state, when intervenes a second pulsation

ω , so that

//, ,mnmnωω≠∈ . Finally, small perturbations of the quasi-periodic

trajectories on a torus (the third bifurcation) lead to a strange (chaotic) attractor. Thus,

from a laminar flow one is led to a turbulent flow (structurally stable), an infinity of

bifurcations – as believed L. Landau – being not necessary. The experiment brought a

confirmation of the theoretical results.

Feigenbaum’s scenario will be presented in Sect. 24.4.2.6.

The route to chaos by intermittency is obtained by a scenario imagined by Yves

Pomeau and Paul Manneville; thus, there can appear “abnormal fluctuations” if a

control parameter leaves a value called intermittency threshold. If the displacement is

small, then the regular oscillations can be interrupted at aleatory intervals of time by

so-called “attacks of turbulence”.

MECHANICAL SYSTEMS, CLASSICAL MODELS

730

24.4.2.4 The Strange Attractors of Lorenz and of Rössler

Trying to model much better the meteorological phenomena, E.N. Lorenz dealt with

the study of the Navier-Stokes equations, written in a simplified form

(),( ),xxyyRzxyzBzxyσ=− − = − − =− + ,

(24.4.32)

where

σ is Prandtl’s number, /

RRR= (

R – Rayleigh’s number,

R – its critical

value) and

is a parameter. We remark that the function ()xt is in direct proportion

with the intensity of the motion of convection, while

()yt is in direct proportion with

the difference of temperature between an ascendent current and a descendent one.

We mention that there exists a symmetry with respect to the

-axis, hence to the

solution (

(), (), ()xt yt zt) corresponds the solution ( (), (), ()xt yt zt−−−) too.

As well, the solution

0, c , 0

xy zz z

−

== = ≠

, of the system tends to the

origin

(0,0,0) for t →∞.

The equations

()0,( ) 0, 0xy Rzxy Bzxyσ−−= −−=−+=

(24.4.33)

give the solutions of equilibrium; there exists only one solution

0xyz=== for

1R ≤ , while for 1R > there exist three solutions, i. e.

0, ( 1), 1xyz xy BR zR=== ==± − =−.

(24.4.33')

One can show that the origin

(0,0,0) is a stable position of equilibrium for 01R<<

and an instable one for

1R > ; the other solutions (24.3.33') are stable positions only

for

RR<< , where

(3)

(1)

σσ

=>+

−+

(24.4.34)

As well, one can show that all the solutions of the system (24.4.12) are bounded.

One sees that there do not exist stable limit cycles, which could lead to periodic

motions, hence to regular motions. Two of the eigenvalues of the Jacobi matrix of the

system (24.4.32) are purely imaginary for

RR= , being thus fulfilled the conditions

imposed by a Hopf bifurcation, which is subcritical; indeed, for

RR<

there exist

two instable periodic solutions around the points corresponding to the stable positions

of equilibrium, while for

RR> these solutions disappear.

Lorenz adopted the values

10σ = and 8/3B = for the parameters of the equation,

being thus led to

24.74

R = ; as well, he took 28R = too. In this case, the set of

solutions contains very complicated orbits, corresponding to a strange attractor

Dynamical Systems. Catastrophes and Chaos

731

(Lorenz’s strange attractor). Simulations on computer put in evidence the presence of

two strata, in which the trajectories have the form of spirals which go away from their

centres; if this distance attains a certain limit, then the solution is ejected from a stratum

and is attracted by the other one, where it describes another spiral a.s.o. (Fig. 24.59).

Fig. 24.59 Lorenz’s strange attractor

The sensibility of the solution to initial conditions can be, as well, put in evidence.

For a deviation

1/100000ε = , an interval of time 1/400tΔ= and 100000 steps

of the computer one obtains the maximal Lyapunov exponent

0.93572L =

(practically

0.9L = ); from the study of the volume variation, we get

0L = ,

14.57L =−

. The presence of the positive exponent

puts in evidence the fact the

motion is chaotic; as well, the dynamical system is dissipative, because the sum of

Lyapunov’s exponents is negative.

The dynamical system being dissipative, we can state that the topological dimension

of the strange attractor vanishes. Using the Kaplan–Yorke conjecture, we obtain

Lyapunov’s dimension of the strange attractor

2.062

D =

Otto Rössler considered, in 1976, a system of differential equations of the form

(), , (),,,constxyzyxayzbxczabc=− + = + = + − = ,

(24.4.35)

which constitutes – perhaps – the most simple model of building up of chaos; we notice

that, in this system, only one of the equations – the third – is non-linear.

Let us suppose, firstly, that

z is very small and can be neglected in the first

equation; we may – as well – take not in consideration the third equation. The system

becomes

,xyyxay=− = +

;

(24.4.36)

eliminating the co-ordinate

y , we can write the equation

0xaxx−+= 

. (24.4.36')