Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

712

If, instead of the system of differential equations

(),

=∈





xfxx , one considers

the system of differential equations

=+xfx gx(), (),εε



positive small parameter, the

heteroclinic and homoclinic lines of the first system are fundamentally changed from a

structural point of view, being thus structurally instable.

24.4 Fractals. Chaotic Motions

In the previously made studies we have encountered the notion of attractor, in the

frame of deterministic motion; this one can be a point, a limit cycle or even a dense

curve on a torus (eventually, in

 spaces, > 3n , on tori of higher order).

Corresponding to chaotic motions, a characteristic attractor has been put in evidence,

i.e. “the strange attractor”; this one has the structure of a fractal, so that a preliminary

study of this motion becomes necessary.

24.4.1 Fractals

The notion of fractal (in Latin “fractus”, irregular) has been introduced by

Benoit B. Mandelbrot, in 1967, and developed by him in the monograph “Les objects

fractals: form, hasard et dimensions”, published in 1975. This denomination can be applied

both to some fractal mathematical sets and to natural fractals (natural forms, which can be

represented by such sets). Mandelbrot put the bases of the fractal geometry, but many

fractals appeared – even if not with this denomination – in the work of great mathematicians

as Georg Cantor, Giuseppe Peano, David Hilbert, Helge von Koch, Wacław Sierpinski,

Gaston Julia and Felix Hausdorff. Mandelbrot showed that such “mathematical monsters”

(Peano’s curve, Hilbert’s curve, Koch’s curve, Menger’s sponge, Hausdorff’s dimension

etc.) are usually encountered in the nature and do not present simple, classical forms, but

forms with a great level of complexity (Mandelbrot, B.B., 1975).

In what follows, after some general considerations concerning the notions of distance

and dimension, we present some methods to generate fractals, as well as the Julia and

Mandelbrot sets.

24.4.1.1 General Considerations

From a descriptive point of view, a fractal is – after Mandelbrot – a set which

presents the same irregularities at any scale they would be seen; from a geometrical

point of view, it is a quantity the parts of which are – in a great measure – identical

with the entire set. This mathematical property is called similarity.

We give some classical examples, in the frame of this definition (Barnsley, M.F.,

1988; Barnsley, M.F. and Demko, S.G., 1989; Falconer, K.J., 1990; Peitgen, H.O., et al.,

1992; Smale, S., 1980).

Let be a segment of a line of length equal to unity, from which we eliminate the

middle third part; further we eliminate the middle third parts from the two segments of a

line which have remained a.s.o., obtaining Cantor’s set. One observes that, reducing the

scale to

1/3,(1/3) ,...,(1/ 3) ,...

, one obtains always the same image (Fig. 24.40).

Let us consider a segment of a line (Fig. 24.41a); we replace the middle third part of

it by a broken line, formed by two segments of a line of length equal to

1/3 of the

length of the initial segment of a line (Fig. 24.41b). We proceed, further, analogously

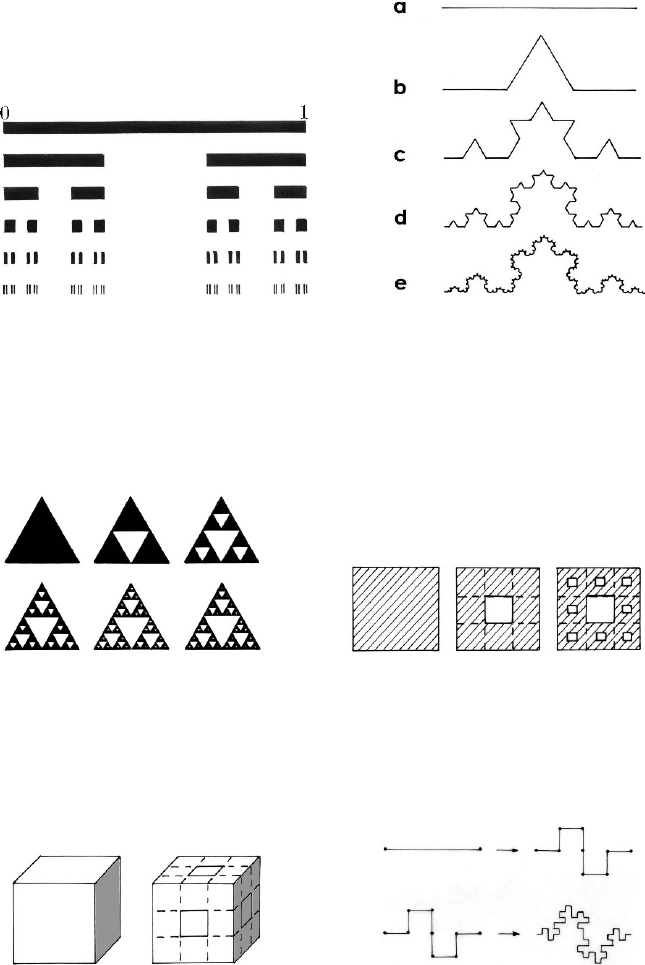
Dynamical Systems. Catastrophes and Chaos

713

with all the segments of a line a.s.o. (Fig. 24.41c–e), obtaining Koch’s curve, which is

continuous, but has not tangent at any point of it (it is of class

C ), Reducing the scale

1/3,(1/3) ,...,(1/ 3) ,...

, one obtains always the same image.

Fig. 24.40 Cantor’s set Fig. 24.41 Koch’s curve

Let be an equilateral triangle, from which we eliminate the median triangle, after

dividing it in four equal triangles; there remain three equilateral triangles, equal to the

eliminated one, from which we eliminate – as well – the median triangles a.s.o. One

obtains thus the Sierpinski sieve (Fig. 24.42); reducing the scale to

1/2,(1/2) ,...,(1/2) ,...

, there results always the same image.

Fig. 24.42 The Sierpinski sieve Fig. 24.43. The Sierpinski carpet

Analogously, we start from a square with the side equal to unity, which we divide in

nine equal squares with the side equal to

1/3; we eliminate the square at the middle,

continue the same operation with the other squares a.s.o., obtaining the Sierpinski

carpet (Fig. 24.43).

Fig. 24.44 The Menger sponge Fig. 24.45 The curve 3/2

MECHANICAL SYSTEMS, CLASSICAL MODELS

714

Let us start now from a cube of side equal to unity; dividing each edge in three equal

parts, one obtains 27 cubes of

1/3 edge, from which we eliminate those on the central

lines. There remain 20 cubes with which we proceed analogously a.s.o., obtaining thus

the Menger sponge (Fig. 24.44).

Starting from a segment of a line of length equal to unity, replacing it by segments of

a line of length

1/4 and continuing the procedure, one obtains the curve 3/2

(Fig. 24.45).

Fig. 24.46 Peano’s curve Fig. 24.47 Hilbert’s curve

If we divide a segment of a line of length equal to unity in three equal parts, build up

a broken line with

9 sides, each one of 1/3 length, and if we continue the procedure,

then we obtain Peano’s curve, which fills a square (Fig. 24.46).

Analogously, we can set up Hilbert’s curve in Fig. 24.47, which – as well – fills a

square.

We notice that all these curves do not pierce themselves.

24.4.1.2 Distances

Let be the points

∈,AB X

; the distance between these points is a function

(, )dAB , ×→:dX X  , with the properties:

(i)

≥(, ) 0dAB ;

(ii)

=⇔ ≡(, ) 0dAB A B;

(iii)

≤+ ∀∈(, ) (, ) (, ), , ,dAB dAC dCB ABC X,

the last property corresponding to the inequality between the sides of a triangle. The

application

d is called metrics and the corresponding space X is a metric space.

Dynamical Systems. Catastrophes and Chaos

715

The points

(,),(, )

Ax y Bx y of a plane being given, the Euclidian distance is

definite by the relation

()()

dxx yy=−+−,

(24.4.1)

the Manhattan distance (the distance between two persons on two orthogonal streets

(one to the other) in the Manhattan district of New York) is given by

dxx yy=−+−,

(24.4.1')

while another definition can be

{

}

max ,

dxxyy=−−.

(24.4.1'')

Let be the sequence of points

123

, , ,...xxx in the space

and another point

∈xX

; we say that x is the limit of this sequence if

()

lim , 0

dx x

→∞

= ,

(24.4.2)

the sequence converging to

x . We notice that the limit does not belong always to the

metric space. A metric space which contains the limit of any sequence of points of this

space is a complete metric space. The set of all the points of a straight line or the set of

all the points of a plane are examples of complete metric spaces for any of the distances

123

,,ddd definite above.

Fig. 24.48 Compact set A; ε – collar set A

Let be a compact set

A ; we call ε -collar set, denoted A

, the set A together with

all the points belonging to the complete metric space

, the distance of which to A is

at the most equal to

ε (Fig. 24.48), i.e.

{

}

|(,) forsomeAxXdxy yA

ε=∈ ≤ ∈.

(24.4.3)

We call Hausdorff distance the distance between the compact sets

A and

defined by

{

}

(, ) inf | andhAB A B B A

εε

ε=⊂ ⊂.

(24.4.4)

All the subsets of a complete metric space

for which the Hausdorff distance has

been introduced form another complete metric space.

MECHANICAL SYSTEMS, CLASSICAL MODELS

716

24.4.1.3 Dimensions

The notion of dimension has been one of the preoccupations of many

mathematicians. At a certain moment, it has been considered that the dimension of an

object is equal to the number of parameters necessary to specify the position of one of

its points. Starting from the dimension zero of a point, Poincaré deduced that a segment

of a line has the dimension one, because a point – with the dimension zero – divides a

line in two parts, a square has the dimension two (because a line divides it in two parts),

a cube has the dimension three (because a square divides it in two parts) etc. Such a

dimension has been called topological dimension, considering that it cannot be changed

if the geometric figure is transformed by a homeomorphism. G. Peano, in 1890, and

D. Hilbert, in 1891, have conceived curves which filled a square, but the transformation

×:[0,1] [0,1]g was not a homeomorphism. A rigorous definition of the notion of

dimension has been given by F. Hausdorff in 1918.

Let be a set of points

∈⊂,

xAA , for which we define the Euclidean distance

(,) ( ), ,

dxy x y xy A

=− ∈

∑

(24.4.5)

⊂

U  , then we call diameter of U

{

}

diam sup ( , ) | ,U dxy xy U=∈.

(24.4.5')

We suppose that the subset

U is open. A family of open subsets

,,...UU is an open

cover of

A if

∞

⊂

∪

(24.4.6)

Being given two positive numbers

> 0s and > 0ε , we define

() inf (diam )

hA U

⎧

⎫

⎨

⎬

⎩⎭

∑

(24.4.7)

where

,,...UU is a cover of the set A with <diam

U ε ; hence

() lim ()

hA hA

ε→

= ,

(24.4.7')

where the limit can be a finite or an infinite number. We call Hausdorff dimension of

the set

A the number ()

DA for which, if < ()

sDA, then we have =∞()

hA ,

while if

> ()

sDA, then =() 0

hA .

For instance, if we cover a segment of a line of length

L by discs of diameter 2ε ,

hence by

/2L ε discs – according to the definition – we have

Dynamical Systems. Catastrophes and Chaos

717

() (2) (2)

ss s

hA L

εε

−

;

hence,

=∞()

hA if < 1s and =() 0

hA if > 1s , the Hausdorff dimension of the

segment of a line being thus

= 1

. Analogously, one can show that

= 2

for a

rectangle and

= 3

D for a parallelepiped.

Let us suppose that we reduce a segment of a line of dimension

to the scale s ; we

notice that there are necessary

=() 1/Ns s reduced segments of a line to remake the

initial one. Analogously, in case of a square or of a cube, there are necessary

() (1/)Ns s or =

() (1/)Ns s such segments of a line, respectively. If D is the

topological dimension, then, in general,

()

= ,

(24.4.8)

wherefrom

log ( )

log

(24.4.8')

One obtains thus the dimension of self-similarity (capacity) introduced by Kolmogorov

in 1958.

For instance, in case of the Cantor set, we notice that at the scale

= 1/1s the

number of the elements is

=() 1Ns , at the scale = 1/3s we have =() 2Ns

elements a.s.o.; at the scale =

(1/ 3)

s will be =() 2

Ns elements. Hence,

()

log ( )

log2 log2

lim lim 0.6309

log 3

log

→∞

====.

In case of Koch’s curve, we see easily that at the scale

= (1/ 3)

s we have

() 4

Ns ; it results thus

()

log ( )

log 4 log 4

lim lim 1.2618

log 3

log

→∞

====.

Sierpinski’s sieve leads to

(1/2)

and

() 3

, wherefrom

()

log ( )

log 3 log 3

lim lim 1.5850

log2

log

→∞

====.

MECHANICAL SYSTEMS, CLASSICAL MODELS

718

For the Sierpinski carpet we have

=() 8

Ns and = (1/ 3)

s , resulting

==log 8 / log 3 1,8928D , while for the Menger sponge = (1/ 3)

s and

=() 20

Ns , so that log 20/ log 3 2.7268D ==.

In what concerns the curve

3/2, we notice that = (1/ 4)

s and =() 8

Ns ,

wherefrom

==log 8/ log 4 3/2D , its denomination being thus justified.

For the Peano curve

(1/3)

and

() 9

and we get ==log9/log2 2D ,

while for Hilbert’s curve

= (1/2)

s and

−

=−

() 4 1

Ns , wherefrom – by passing to

limit –

==log 4/ log2 2D , hence the same dimension.

If we wish to measure practically the length of a rectifiable curve, then we inscribe in

this curve a polygonal line for which we can measure the lengths of the sides; e.g., in

the case of a circle of unit radius, by inscribing an equilateral triangle, one obtains the

length of the circumference

== =

3 3 3 5.1962Ll , by inscribing a regular

hexagon, it results

==⋅=

6 6 1 6.0000Ll , by inscribing a regular dodecagon, we

will have

==−=−=

12 12 2 3 6( 6 2) 6.2117Ll a.s.o.; if the number of

the sides of the regular polygon increases indefinitely, then the length

L tends to 2π .

Lewis Fry Richardson, wishing to calculate the length of the west coast of Great

Britain, arrived at unexpected conclusions; indeed, assuming that one cannot make

measurement along the coast, but only on the map, e.g., at the scales

1 : 1000000 , and

– using a compass – by which to

3 cm correspond 30 km, one obtains a certain length

L . Taking then smaller lengths or using maps with smaller scales (1 : 500000 or

1 : 100000 a.s.o.), one obtains values which increase indefinitely. Indeed, using maps

at smaller scales, one finds new gulfs, new peninsulas etc. To can measure such a

length, Richardson proposed an empiric formula of the form

()

LFεε

−

= ,

(24.4.9)

where

ε is the length taken by the compass, while F and D are two characteristic

constants; he assumes that

F is the searched length, but for D he did not find an

interesting significance. By a different choice of

ε , there can result sufficient great

differences, till

−20 25% ; e.g., the length of the common frontier between Spain and

Portugal is considered to be

987 km in the Spanish encyclopedia and 1214 km in the

Portuguese one.

Mandelbrot considered that the number of sides

()N ε is much more important in

the measurement of the above length; from (24.4.9) it results that

()

NFεε

−

= ,

because

() ()NLεε ε= . Assuming that one has not to do with a length, but with a

body of dimension

, we can multiply by

ε , so that

FFεε

−−

−=; it results

that

F is just the searched length (as it has been supposed by Richardson), while D is

of the nature of a dimension, called compass dimension or fractal dimension. This

dimension coincides with that of self-similarity.

One can define also the informational dimension

D (which is always smaller or at

least equal to the dimension of capacity), the correlation dimension

, the punctual

dimension

D etc.

Dynamical Systems. Catastrophes and Chaos

719

In very complicated cases, e.g., in the case of a “wild fractal”, as in Fig. 24.49, one

can use the method of “box counting”, a systematic measurement which can be applied

both in the plane and in the tree-dimensional cases. In the plane case, one covers the

structure by a net with square eyes of side

s and one counts the squares which contain

parts of the structure, obtaining

()Ns; choosing various sides s , we note in the plane

the points of co-ordinates

log(1/ )s and log ( )Ns , and then one draws a straight line

as near as possible to these points. The inclination of this straight line is called the

box-counting dimension

D . This method leads practically to the same fractal

dimension for Koch’s curve and for the curve

3/2.

Fig. 24.49 Wild fractal

24.4.1.4 Methods to Generate Fractals

Starting from the property of similarity, the fractal is a theoretical notion; but the

mathematical fractal is a model for the natural fractal.

We mention that the fractals intervene not only in statical phenomena, but also in

dynamical ones.

Studies of this nature have been made both at micro and at macro scales; e.g., after

Mandelbrot, the fractal dimension of the Universe is

1.23D = .

We call fractal a set for which the topological dimension

D is less than its compass

(fractal) dimension.

DD< .

(24.4.10)

Corresponding to this definition, the Cantor set (

0log2/log3

DD=< = ),

Koch’s curve (

1log3/log2

DD=< = ), Peano’s curve ( 12

DD=< =),

Sierpinski’s sieve (

1log3/log2

DD=< = ) are fractals.

We obtain thus a language which allows to build up a geometry of fractals. As

simple elements, we consider the affine transformations of the form

,uaxbyevcxdyf=++ =++

(24.4.11)

in the plane, which transform the point

(,)xy into the point (,)uv , e.g., a rectangle

into a parallelogram.

MECHANICAL SYSTEMS, CLASSICAL MODELS

720

In particular, if

1, 0, , 0ad bc ef== == ≠

, that is if

,uxevyf=+ =+,

(24.4.12)

then it results a translation; if

cos , sin , 0ad b c efϕϕ= = =− =− = = , hence if

cos sin , sin cosux y vx yϕϕ ϕϕ=− =+

(24.4.12')

then one obtains a rotation; if

01, 0ads bcef<==< ====, that is if

,,01usxvsy s==<<,

(24.4.12'')

then one gets a reduction by similitude; if

01, 0ad bcef<≠< ====

, hence if

,,0 1uaxvdy ad==<≠<,

(24.4.12''')

then it results an affine reduction; if

1, 0ad bcef=− =− = = = = , that is if

,uxvy=− = ,

(24.4.12

)

then one obtains a mirror symmetry (with respect to the

Oy -axis); if

1, 0, 0ad b cef== ≠ ===, hence if

,uxbvy=+ =,

(24.4.12

)

then one gets a shearing (in the direction of the

Ox -axis).

The transformations mentioned above are considered being operators:

,,...,

WW W; assuming that the operators are applied on a set A , we may write

() () () ... ()

WA W A W A W A=∪∪∪,

(24.4.13)

obtaining Hutchinson’s operator.

Let us image an iterative application of this operator in the form

112 1

( ) , ( ) ,..., ( ) ,...

WA AWA A WA A

== =;

(24.4.14)

the succession of images thus obtained can tend to

∞

, for which takes place the relation

()WA A

∞∞

= .

(24.4.14')

In general, the set

∞

is a fractal, which appears as a fixed point of Hutchinson’s

operator. One has thus a convenient method to generate fractals.

For instance, let us consider operators functions of only one variable

Dynamical Systems. Catastrophes and Chaos

721

333

WW==+

(24.4.15)

respectively, the first one corresponding to a contraction in the ratio

1/3 and the

second one corresponding to the same contraction, followed by a translation of

2/3.

Using Hutchinson’s operator

WW W=∪

a.s.o., we obtain Cantor’s set (Fig. 24.50).

Fig. 24.50 Cantor’s set, obtained using Hutchinson’s operator

Analogously, one can generate both Koch’s curve and Sierpinski’s sieve.

Using Hutchinson’s operator defined by

0.85 cos(2 30 ) 0.85 sin(2 30 ),

(,)

0.85 sin(2 30 ) 0.85 cos(2 30 ) 1.6,

0.3 cos(49 ) 0.34 sin(49 ),

(,)

0.3 sin(49 ) 0.34 cos(49 ) 1.6,

0.3 cos(120 ) 0.37 sin(50 ),

(,)

ux y

Wxy

vx y

ux y

Wxy

vx y

ux y

Wxy

′′

⎧

⎪

⇒

⎨

′′

=− + +

⎪

⎩

=−

⎧

⎪

⇒

⎨

=+ +

⎪

⎩

⇒



0.3 sin(120 ) 0.37 cos(50 ) 0.44,

(,)

16 ,

Wxy

⎧

⎪

⎨

=++

⎪

⎩

⎧

⎪

⇒

⎨

⎪

⎩



(24.4.16)

we can start from a rectangle as initial image, obtaining Barnsley’s fern (Fig. 24.51),

hence a sufficiently sophisticated natural fractal.

The geometry of fractals can thus be a method of investigation in the science of

complexity.

B. Mandelbrot showed in 1977 that the Julia set, defined by the recurrence relation

zzc

(24.4.17)

where

and c are complex numbers, introduced by G. Julia in 1918, is – in fact – a

fractal. It has been thus shown that the attraction basins of the three cubic roots of the

unity:

1, ( 1 3i) / 2−± are limited by fractals (not by curves, as believed Cayley).