Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

352

()

=δ+δ+δ++δ−δ

∫

22 33 1

...

Iztpqpq pqKq

(21.1.33)

preserving the aspect of the Poincaré-Cartan integral. Thus, the motion of the system

will be described by Hamilton’s differential equations

∂∂

==−

∂∂

===

∂∂

, , 2,3,..., ,

tKz

qzq

qpqq



(21.1.33')

where

q is the independent variable.

For instance, in case of the linear oscillator, for which

=+=−

Hpqz

(21.1.34)

we obtain

=− = − −

2Kpmzkq;

(21.1.34')

the canonical equations will be

−−

d1d

tm z

qk q

being thus led to

, constzhh=− = , and to

=+= +

−

∫

arcsin

ωϕϕ

wherefrom

()

=−==

sin , ,

qa t a

ωϕ ω ,

(21.1.34'')

ϕ being an arbitrary constant.

21.1.2.5 Integral Invariants and Differential Forms

We have introduced in Sect. 19.1.1.9 the Pfaff form of Hamilton (19.1.45), which is

a form of first degree definite on the space of states

=×

21s

SEΓ (

E is the space of

time). More general, we introduce on

S the form of second degree, independent on the

local system of canonical co-ordinates,

Other Considerations on Analytical Methods in Dynamics of Discrete Mechanical Systems

353

=∧−∧dd ddd

pqHtω ,

(21.1.35)

where we use the exterior product (see. App., Sec. 1.2). Let be a family of solutions of

the canonical equations

(; ),

qqtλ= (; ),

pptλ=

{ , ,..., },

λλλ λ≡

1,2,...,is= , which depends on the parameters ∈=[ , ], ,2,...,

jjj

ab j rλ ; thus, it is

defined a differentiable and one-to-one transformation →

:TSΛ of a domain Λ of

the space

(, )t λ into S .

Let us consider a domain

⊂

XE , a domain ⊂

YE and a differentiable

application

→:TX Y. As well, let be the function (form of zero degree)

→

:fY \

by composition with T one obtains the function (a form of zero degree

too)

∗

=Tf f TD , defining the application

∗

→

:() ()TFY FX

. In general, one

can define the application

∗

→:() ()

TFY FX , which maps forms of degree p ,

defined on

, into forms of degree

, defined on

. We mention the basic properties

of the application

T :

(i)

+= +

***

12 1 2

()TTTωω ω ω,

(ii)

∧= ∧

***

12 1 2

()()()TTTωω ω ω

(iii)

d( ) (d )TTωω,

(iv)

→→⇒ =

***

12 21

:,: ()TX YTY Z TT T TDD.

Observing that the form (21.1.35) can be written in the form

∂∂

⎛⎞⎛⎞

=+ ∧−

⎜⎟⎜⎟

∂∂

⎝⎠⎝⎠

dd d d d

ptqt

(21.1.35')

and taking into account the canonical equations, we get

∂∂

=∧= ∧

∂∂

∑∑

,1 ,1

(d ) d d ( ; ) d d

kjk k

jk jk

TAt

ωλλλλλ

λλ

Poincaré’s Lemma (

=d(d ) 0ω ; see App. , Subsec. 1.2.2) leads to =

d( (d )) 0T ω ; it

results, further,

= 0



, so that

(d )T ω

does not depend on time.

We say that a differential form

Ω of degree p , defined on S , is an absolute integral

invariant if, for any transformation

T , defined on a family of trajectories which depend

r parameters =, 1,2,...,

jrλ ,

T Ω is an independent p -form of t and dt , on

the space

λ , and if

=d0Ω

The forms

∧∧

d ,( d ) ,...,( d )

ωω ω are integral invariants, in this case, because

⎡⎤

∧= ∧=∧∧ =

⎣⎦

d( d ) 0, ( d ) ( d ) , 1,2,...,

TTpsωω ω .

MECHANICAL SYSTEMS, CLASSICAL MODELS

354

Starting from the above definition, one can show that integrating

Ω on any chain

transverse to a family of trajectories one obtains a constant; hence, any invariant in the

sense of this definition is invariant in the sense of the classical definition.

We say that a

p -form Ω is a relative integral invariant if dΩ is an integral

invariant. Thus, because

dω is an absolute integral invariant, it results that ω is a

relative integral invariant (the Poincaré-Cartan invariant). We can state that the forms

∧∧∧ ∧∧

d , ( d ) ,..., ( d )

ωωω ω ω ω

are, as well, relative invariants, because

[

]

∧∧ =∧

d(d)(d)

ωω ω.

If the points which correspond to transverse chains represent simultaneous chains

(for

consttt==

and

consttt==

), then

=d0t

. Poincaré’s invariant will

correspond to

ω . As well, starting from =∧ddd

qpω and observing that

−

∧= ∧∧∧∧∧∧

=− ∧ ∧ ∧ ∧ ∧ ∧ ∧

1122

(1)/2

12 12

( d ) ( !)d d d d ... d d

( 1) ( !)d d ... d d d ... d ,

sq p q p q p

sq q q p p p

we get Liouville’s invariant.

21.1.3 Ergodic Theorems

In what follows we present the recurrence theorem of Poincaré; starting from it, we

put in evidence the so-called ergodic theorems.

21.1.3.1 Poincaré’s Recurrence Theorem

Let be an autonomous system (where the time does not appear explicitly)

( , ,..., ), 1,2,...,

xXxx xj s==



(21.1.36)

which has the properties:

(i) Its divergence vanishes (

∂∂=/0

Xx ), so that the extension in space is

invariant to a transformation

T definite by the solutions of the considered system; in a

mechanical image, we say that “the fluid is incompressible”. Obviously, this condition

holds in the case of Hamiltonian systems.

(ii) There exists a closed domain

Ω

of finite extension for which the characteristics

which start from its points are entirely in

Ω ; we say that “the fluid is moving in a

closed vessel”. Such a domain is transformed in itself by

T and is called invariant

domain.

We can state

Theorem 21.1.8 (of recurrence; H. Poincaré). For any closed subdomain

ω of Ω , no

matter how small, there exist characteristics which pass through it an infinity of times.

More precisely, for any moment

t , no matter how great, there exist motions of the

system for which the movable point is in

ω at a moment

. Poincaré called such a

Other Considerations on Analytical Methods in Dynamics of Discrete Mechanical Systems

355

motion, in which the system returns an infinity of times to the neighbourhood of the

initial state, “stable in Poisson’s sense”.

The central idea of demonstration of this theorem is Liouville’s theorem; no

particular property of Hamilton’s equations is used.

Poincaré’s theorem can be a starting point for new studies concerning problems of

classical dynamics. Usually, we wish to solve these problems determining explicitly the

configuration of the system at the moment

t , as a function of t and of the given

configuration at the moment

tt; but for the most problems one cannot find exact

solutions. Poincaré’s theorem plays an important rôle in this case; one can determine

the individual characteristics starting from a discussion of statistical properties of these

characteristics, taken as a whole.

Let be a mechanical system for which

H is inferior bounded in the phase space. We

can suppose that

=inf 0H

; this can be obtained by adding a convenient arbitrary

constant (which does not alter the equations of motion). Let us suppose that “the

surface”

, const, 0Hhh h== >, is closed. In this case, H is a first integral of the

canonical system and the surface

=Hh bounds an invariant domain; the domain

bounded by two such surfaces will be, analogically, an invariant domain. In case of the

system

==−,qpp q,

(21.1.37)

corresponding to a harmonic oscillator, we choose the unity of time so that the period

2π . The system has only one degree of liberty, hence the phase space is

two-dimensional, while the trajectories are the curves

= constH , hence the circles

()

+=>

qp hh

;

(21.1.37')

the motion on each circle is uniform and clockwise. The circle

=+= >

,0rqpRR, is an invariant domain, which contains only one

trajectory. The domain

RrR is an invariant domain too. The motion of the

fluid is a motion in which the fluid is rotating as a rigid solid. Hence, the domain

Ω

may be a circle, a circular disc or a circular annulus.

21.1.3.2 Ergodic Theorems

Poincaré’s theorem states the existence of the motions in which the movable point

re-enters in

ω an infinity of times. Further, following problem is put: How long is the

movable point in ω ? As well, the problem is put in case of discrete intervals of time:

In what proportion (of time) is the movable point in

ω ? The theorems connected to

such problems and to analogous ones are called ergodic theorems.

In connection with such problems appears the necessity of integration on a set of

points; one must use Lebesgue’s measure of a set of points instead of the simpler set of

volume or extension, sufficient till now, and the integrals will be Lebesgue integrals

instead of Riemann ones (sufficient, usually, in classical mechanics).

Let be the transformations

defined by the solutions of the autonomous system

(21.1.36) of zero divergence; let be also an invariant domain

Ω

of finite measure

mΩ

MECHANICAL SYSTEMS, CLASSICAL MODELS

356

We consider a function of position

()fP, definite and summable on

Ω

. We denote by

the point which is reached by the point

by means of the transformation

; in

other words, the movable point which starts from

at the moment

reaches

the moment

t . We will be interested on the mean value (with respect to time) of the

function

()fP on a portion of the trajectory (let be the trajectory which starts from the

point

A ), travelled through by the movable point from the moment

=ta

to the

moment

=tb

; let be

−

∫

() ( )d

AfAt

(21.1.38)

The existence of the mean value

()

Aμ

for nearly all the points ∈A Ω results from

the summability of

()fP, according to Fubini’s theorem; we exclude from the above

considerations the set of null measure of the points

A , for which the above mean value

does not exist. We can state

Theorem 21.1.9 (ergodic). The mean value

()

Aμ

tends to the limit ()Aϕ together

with

→∞b for almost all the points ∈A Ω

The proof of the theorem is made in two steps; one effects firstly a passing to limit

by entire values and then one passed continuously to the limit.

()Aϕ exists for a particular value of A , let be

()Aϕ , then it exists for all the

points

A , on the trajectory through A , having the same value in all these points. In

certain hypotheses, we can go farther, stating that

()Pϕ is constant not only along the

trajectory, but is constant on

Ω

too. This property of invariant domain is fundamental

in statistical mechanics. It does not state for Hamilton’s equations in classical dynamics;

to take place in this case too,

Ω

must be indecomposable (one must not have

=∪

ΩΩ Ω

, where

Ω

and

Ω are disjoint invariant domains of positive measure).

21.2 Periodic Motions. Action-Angle Variables

After the presentation of periodic and quasi-periodic motions, one introduces the

action-angle variables, useful for solving the respective problems. The important rôle

played by the adiabatic invariance is then put in evidence (Pars, L., 1965; Santilli, R.M.,

1984).

21.2.1 Periodic Motions. Quasi-Periodic Motions

The motions of planets and the atomic phenomena have, in general, a character of

periodicity; the study of the periodic motions has thus a great importance, both to

celestial and quantum mechanics. Other natural motions are only quasi-periodic

(conditionally-periodic). The respective problems play an important rôle in classical

quantum mechanics.

Other Considerations on Analytical Methods in Dynamics of Discrete Mechanical Systems

357

21.2.1.1 Periodic and Multiply Periodic Motions

Let firstly be the case of a dynamical system which has only one degree of freedom,

to which corresponds the variable of position

q . Let us suppose that one can make a

canonical transformation

→(, ) ( , )qp wα , so that the canonical system be reduced to

= constα

, w being a circular function of time; one obtains thus a periodic motion. If

there exists a

w so that

+=()()qw qwω ,

(21.2.1)

then one obtains a phenomenon of libration (the generalized co-ordinate

q oscillates

between two limit positions), e.g., the oscillatory motions of the pendulum. If the

mechanical system returns to the same position after a certain variation of

q (let be

2π

), which is effected repeatedly, in the same interval of time, so that

+= +()()2qw qwωπ,

(21.2.1')

then the motion is a rotation (e.g., the motion of rotation of the pendulum).

In the following, we consider separable and periodic, generalized conservative

mechanical systems. Because =



, the complete integral of the Hamilton-Jacobi

equation (19.2.9) will be given by (19.2.15'), where

ah; by separation of variables,

the function

S will be of the form (19.2.41). On the other hand, it results

===

( ; , ,..., ), 1,2,..., ,

jjj

ppqaa aj sah.

(21.2.2)

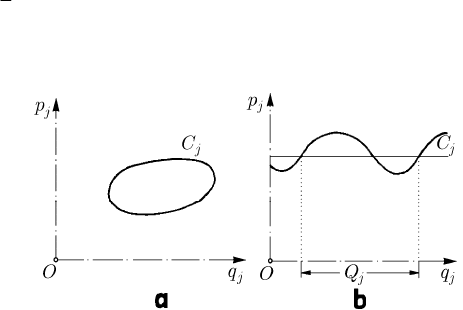
Fig. 21.5 Motion of libration (a); motion of rotation (b)

We say that the motion is multiply periodic if the conjugate canonical co-ordinates

()and ()

qt pt admit the same period

T (the projection of the representative point on

the plane

(, )

qp describes a closed curve

C , corresponding to a motion of libration

(Fig. 21.5a)) or if any generalized momentum

p is a periodic function of

q , with the

period

Q (the projection of the representative point on the plane (, )

qp describes a

periodic open curve

C , corresponding to a motion of rotation (Fig. 21.5b)).

For instance, in case of an anisotropic linear oscillator, the components of the elastic

force are

− (!)

kx ; there results the Hamiltonian

MECHANICAL SYSTEMS, CLASSICAL MODELS

358

∑∑

Hpkx

(21.2.3)

The relations (21.2.2) are given by

+== ++=

123

,1,2,3, 2

jjjj

pmkx aj aaa mh,

(21.2.3')

the obtained closed curves

C being ellipses (motion of libration).

In case of a mathematical pendulum, Hamilton’s function is given by

=−

cos

Hpmgl

θ ,

(21.2.4)

the generalized momentum being

=()Hh

()

2cospmlhmgl

θ ;

(21.2.4')

hmgl

, then the generalized momenta p

vary periodically and θ increases

unlimited (motion of rotation).

21.2.1.2 Linear Periodic Motions

In the case in which we have only one degree of freedom, the canonical equations are

∂∂

==−

∂∂



(21.2.5)

with Hamilton’s function

=−

() ()

HfqpUq

(21.2.5')

where

()Uq is the potential of forces; there results the reduced Hamilton–Jacobi

equation

∂

⎛⎞

⎜⎟

∂

⎝⎠

() 2( )

fq U h

(21.2.6)

h being the constant of energy. Integrating this equation, we get

∫

2( )

()

(21.2.6')

so that

∂

−= =

∂

∫

2( ) ( )

Uhfq

(21.2.6'')

Other Considerations on Analytical Methods in Dynamics of Discrete Mechanical Systems

359

The study of the motion depends on the study of the equation

≡+ =() 2( )() 0qUhfqϕ .

(21.2.7)

One can show that

q cannot pass beyond a value

q , a real root of the equation

=() 0qϕ (we have at any moment <>

orqq qq). Often, q oscillates between two

limit values

<<qαβ; in general, taking into account the preceding result, if α and

>βα are two real roots of the mentioned equation, then

can vary in the interval

(,)αβ or can remain outside this interval, as – at the initial moment – q belongs or not

to the respective interval.

q and

q are multiple roots of order of multiplicity m and n , respectively, we

can write

==− −

() ( ) ( ) ()

qqq qqϕαβψ ,

(21.2.7')

where

()qψ does not have roots in the neighbourhood of α and β . A change of

independent variable

, by the relation

()

(21.2.8)

where

ν is a non-determinate constant, allows a more convenient analysis of the

differential equation (21.2.7'). One takes the sign + before the radical, so that

w does

vary in the same sense as

t ; as well > 0ϕ , because it cannot change of sign in the

considered interval, being a continuous and finite function of

q . One obtains

=− −

()()

να β ,

(21.2.8')

from (21.2.7') and (21.2.8).

We get the integral

() cos sin

qw w w

νν

αβ,

(21.2.9)

in the particular case

==1mn ; hence, q is a periodic function of w , of period

2/πν. The constant ν is determined by the condition that q be a periodic function of

time, of period

−−

∫∫

() ( )( ) ()

qqqq

πν

ψαβψ

(21.2.9')

where

q is given by (21.2.9). It results thus a motion of libration, the limits

q and

being reached by

q .

MECHANICAL SYSTEMS, CLASSICAL MODELS

360

m and n differ from unity, then one can make an analogous study; in this case,

d/dqw does not change of sign, q nearing asymptotically one of the two frontiers (

and

q ), without reaching it in a finite time.

21.2.1.3 Quasi-Periodic Motions

Let us consider now a generalized conservative dynamical system with

> 1s

degrees of freedom; assuming that the system is with separate variables, we use

Stäckel’s theory (see Sect. 19.2.2.3). Let

α and

β be two isolated consecutive zeros

of multiplicity

and

, respectively, of the function ()

qϕ , specified by

(19.2.58), so that the initial values do satisfy the relations

<< =

, 1,2,...,

jj j

qj sαβ .

In this case

=− − =( ) ( ) ( ) ( ), 1,2,...,

jj j j j j jj

qq q qj sϕαβψ ,

(21.2.10)

with

> 0

ψ and without any other zero in the considered interval.

Let us make the change of variable

=− − =

/2 /2

d ( ) ( ) d , 1,2,...,

jjj jj j

qq q uj sαβ

;

(21.2.11)

as well, let us denote (see Sect. 19.2.2.3)

()

( ) , , 1,2,...,

()

fq jk s

(21.2.12)

According to the lemma in the preceding subsection, the variables

q remain in the

interval

(,)

αβ , the motion being thus a libration. We consider thus the more simple

case in which

==1

mn , case in which all variables have a variation of libration.

We obtain

=+ =

cos sin , 1,2,...,

jj j

qjsαβ

(21.2.13)

in this case; introducing in (21.2.12), we can calculate

∫

()d

fq u

(21.2.12')

The quantity

=+−

2(2)()

jk jk

χχ

ωπ

is constant, because

is a periodic function of

; we have

Other Considerations on Analytical Methods in Dynamics of Discrete Mechanical Systems

361

== =

−−

∫∫

()d

( )d , , 1,2,...,

()()()

jk jk

jjjjjj

fq u jk s

qqq

πβ

αβ ψ

(21.2.14)

We introduce the new variables

, 1,2,...,

wj s= , by means of the relations

== − =+

∑∑

, , 1,2,..., 1,

jjsj

jk k

wbjk s wtbωω,

(21.2.15)

as in Sect. 19.2.2.3. Assuming that

≠det[ ] 0

ω , it results =

(,,..., )

qqww w,

with

, , const, 1,2,...,

jj jjj

wt j sνγνγ=+ = = .

If the frequencies

ν are commensurable (are of the form ,

jjj

nnνν=∈` ), then

the motion is periodical; otherwise, the motion is similar to a Lissajous one. In such a

motion, the trajectory passes as much as possible near to any point in

Λ ; it satisfies the

quasi-ergodic hypothesis: the trajectory fills everywhere dense the whole domain of

co-ordinates. The motions which fulfil this condition care called quasi-periodic;

(conditional periodic) motions; as examples of problems which lead to such motions,

we mention: the problem of two particles, the problem of two centres, the spherical

pendulum etc.

21.2.2 Action-Angle Variables

In what follows, we introduce the action variables and the angle variables, useful to

solve the above mentioned problems; we present then some applications.

21.2.2.1 Action Variables. Angle Variables

We introduce the variables (without summation)

∫

jjj

Jpq

(21.2.16)

of the form

( , ,..., ), 1,2,...,

JJaa aj s== (taking into account (21.2.2)), called

action variables; obviously, these integrals are areas (see Fig. 21.5a). There result

( ), { , ,..., }, 1,2,...,

aaJJJJ Jk s=≡ =, so that the complete integral of the

reduced Hamilton-Jacobi equation becomes

= (, )SSqJ,

(21.2.17)

Hamilton’s function (due to the first integral of the energy, we have

=Hh

) will be of

the form

==()HHJ h,

(21.2.17')

where we took into account the modality to introduce the constants

a . We notice that

the function (21.2.17) plays the rôle of a function

S generating canonical