Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

Variational Principles. Canonical Transformations

331

20.3.3.8 The Galileo–Newton Group

Let

E be the Euclidean space spanned by the vectors

()

123

,,; ;xxxt=≡xrt.

The Galileo–Newton group

G is the group of endomorphisms of

E , of the form

′

=++

rRrva, ttτ

′

(20.3.97)

and it consists of a time translation, defined by

τ, a translation in

EE⊂ , defined by

E∈a

, a transformation of the form (20.3.79) from the Galileo group

and a

rotation

SO(3, )∈ \R of the space

. The Galileo-Newton group is a subgroup of

the affine group in four dimensions or, in homogeneous co-ordinates, a subgroup of the

general linear group

()

GL 5, \ .

The time interval between two events in the space

E ,

tt tΔ =−, as well as the

spatial distance between two simultaneous events

Δ =−rrr,

tt= , are

invariant with respect to the transformations of

G. Reciprocally, the Galileo–Newton

group is the most general group of linear transformations in

E , which preserves the

intervals

tΔ and Δr . The elements of the Galileo-Newton group G depend on ten

parameters, and are denoted by

()

,,,τgavR. The induced composition law is defined

()

,,, ,,, , , ,ττ τττ

′′ ′ ′ ′ ′ ′′ ′ ′

=+++ +g a v R g a v R g a Ra v v Rv RR

(20.3.98)

The identity element of the group is

()

0, , ,g001, where 1 is the identity element in

SO(3, )\ , while the inverse of a given element is

()

,,,τ

−

==ggavR

()

111

,( ), ,ττ

−−−

=− − −gRavRvR. The Galileo–Newton group is isomorphic to the

group of matrices

()

0001

0000 1

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

→=

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

gtg

(20.3.99)

of order five, which depend on ten parameters and satisfy the relation

()()()

12 1 2

=tgg tg tg ,

(20.3.99')

identical with the internal composition law (20.3.98).

We will outline now some results from the theory of the Galileo–Newton group.

Thus, it can be shown that the group G is a non-compact Lie group. The most

important subgroups of the Galileo–Newton group are:

MECHANICAL SYSTEMS, CLASSICAL MODELS

332

(a)

()

{

}

,,,τ=T g001

– the group of time translations,

(b)

()

{

}

0,,,T = ga01

– the group of space translations in

E ,

(c)

()

{

}

0, , ,Γ = g0v1

– the Galileo group,

(d)

()

{

}

SO(3, ) 0,,,=\ g00R

– the group of proper rotations in

E .

The direct product of the groups

T×T forms an invariant Abelian subgroup of G,

and the corresponding factor group is the semi-direct product

SO(3, )Γ ∧ \ , that leads

to the decomposition

SO(3, )()( )T Γ ∧=×∧ \GT .

(20.3.100)

Note that there are also other decompositions of

G, like the following one

SO(3, )()( )T Γ ∧=×∧ \GT,

(20.3.100')

where

T Γ× is the maximal invariant Abelian subgroup of G.

The basis of the Lie algebra associated to

G comprises ten elements corresponding

to the subgroups

T, T, Γ , and SO(3, )\ . Consequently, the first integrals obtained

from the invariance of the Lagrangian with respect to these subgroups, determine the

generators of the Lie algebra, corresponding to the relation (20.3.60). Thus, we obtain:

(

α )

– the generator of

(β )

P , 1, 2, 3k = ,

– the generators of T,

(

γ )

ξ , 1, 2, 3k = ,

– the generators of

Γ ,

(

δ )

(1/2)

ijk jk

=∈KK, 1,2, 3i = , – the generators of SO(3, )\ .

Hence, the generator of an infinitesimal transformation of

G has the form

ij ij i i i i i i i i i i

av avδε δ ξ δ δτ δθ δ ξ δ δτ=+++=+++XK P H K P H.

(20.3.101)

The matric form of these generators follows from the representation (20.3.99). We

can also obtain these generators in the form of differential operators. Thus, we consider

the space of square integrable functions (;)ftr , defined on

E . Then, we obtain the

regular representation of

G as the set of differential operators u acting in the space of

the functions f, defined by the equation

()()

()

,,, ; ( ),ft f t tτττ

−

=−−+−uavR r Rrvav .

(20.3.102)

Finally, we obtain the basis of the Lie algebra associated to

G, as the set of generators

∂

H , = ∇P ,

∇ , =×r ∇K ,

(20.3.103)

Variational Principles. Canonical Transformations

333

that satisfy the commutation relations

()

ijk k

=∈KK K,

()

ijk k

=∈

ξξ

K ,

()

ijk k

=∈KP P,

()

=ξ HP,

()

()()

()

()()

00 0

,, , , ,,0

i ijijiji

ξξ ξ======KH P PP PH HH .

(20.3.103')

The subgroup structure of

G can be determined by means of the Lie subalgebras which

may be identified on the basis of these commutation relations. From (20.3.103') we can

also obtain the two invariants of the Galileo–Newton group

P = P

()

N =×Pξ .

(20.3.104)

The invariance of the Lagrangian of a mechanical system with respect to the

Galileo–Newton group is the necessary and sufficient condition for the conservation of

the generalized linear and angular momenta, of the generalized mechanical energy and

of the uniform rectilinear motion of the centre of mass. The corresponding Lagrangian

has the form (20.3.85). It is easy to show that, under the transformations of the Galileo-

Newton group, the mechanical energy and the momentum of a free particle are

transformed according to the relations

()

EE m

′

=+⋅ +vRp v, m

′

=+pRp v.

(20.3.105)

It follows that

VE E

′′

=− =−pp,

(20.3.106)

i.e. V is invariant with respect to the transformation of

G. To prove (20.3.106) we used

the invariance of the dot product with respect to

SO(3, )\ , that is

()()⋅=⋅Rp Rp p p .

From a mechanical point of view, V represents the difference between the

mechanical energy and the kinetic energy of the particle, that is the energy of the

particle at rest (

=p0); hence, we may say that V represents a sort of “intrinsic energy”

(of the nature of a potential energy) of the particle. It is worthwhile to mention that,

while in the relativistic mechanics the existence of the rest energy of a particle is an

obvious result, a similar energy appears here in the context of classical mechanics, from

considerations on the symmetry properties of the Lagrangian in a four-dimensional

Euclidean space-time.

Chapter 21

Other Considerations on Analytical Methods in Dynamics

of Discrete Mechanical Systems

Closely connected to the canonical transformations, one can introduce the notions of

integral invariant and of ergodicity. The action-angle variables, useful in the study of

periodic motions, are then considered.

The methods of exterior differential calculus prove their importance to mathematical

modelling of the phenomena of nature, in particular to mathematical modelling of

mechanics; in this order of ideas, we will present some elements of invariantive

mechanics. Besides the formalisms in the spaces

Λ and

Γ , other formalisms can be

used in various cases; we mention thus the Birkhoffian formalism, applicable to a larger

circle of problems than of the Lagrangian and Hamiltonian formalisms.

The theory of control will allow then a profound insight into optimal trajectories.

21.1. Integral Invariants. Ergodic Theorems

After some results concerning the integral invariants of order

, one passes to a

study of the integral invariants of first order. As well, one makes some general

considerations concerning ergodic theorems (Arnold, V.I., 1976).

21.1.1 Integral Invariants of Order 2s

In what follows one introduces the notion of integral invariant and one gives some

corresponding general results; one passes then to the case of the absolute integral

invariant of order

2s .

21.1.1.1 Notion of Integral Invariant. General Considerations

We return to the system of differential equations (15.1.22), written in the form

12 2

( , ,..., ; )

xXxx xt ,

1,2,...,2

(21.1.1)

for

=+21ns; if the functions

X and / , , 1,2,...,2

Xxjk s∂∂ = , are definite and

continuous in a neighbourhood

of the point (

00 0

12 2

, ,..., ;

xx x t), then there exists a

neighbourhood

⊂UU

in which the solutions of this system of differential equations is

obtained by means of the first integrals (15.1.23). The initial conditions of Cauchy type

335

P.P. Teodorescu, Mechanical Systems, Classical Models,

MECHANICAL SYSTEMS, CLASSICAL MODELS

336

allow to determine the integration constants so that through any point

∈

000 0

12 2

( , ,..., )

Pxx x D does pass an integral curve (according to the theorem of

existence and uniqueness)

00 0

12 2

( ; , ,..., ), 1,2,...,2

xxtxx xk s,

(21.1.2)

and only one; vectorially, we can write (we consider

-dimensional vectors)

=rrr

(; )t .

(21.1.2')

As well,

()

⎡⎤

∂

=≠

⎢⎥

∂

⎣⎦

12 2

00 0

12 2

, ,...,

det 0

, ,...,

xx x

(21.1.2'')

so that we also may calculate

12 2

( ; , ,..., ), 1,2,...,2

xxtxx xk s

(21.1.2''')

=rrr

(, )t ,

(21.1.2

)

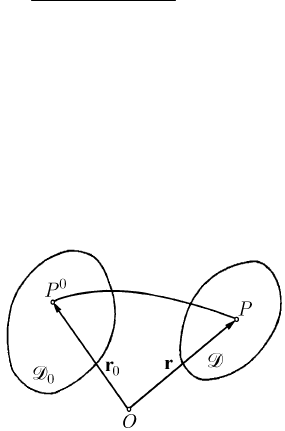
Fig. 21.1 Transformation of the domain

D into the domain D

A representative point

P corresponds to the state of the mechanical system for

, in the phase space

, so that

D represents a set of possible states of the

system. If we fix

, then the trajectory of the representative point which passes

through

is given by (21.1.2'). If we fix t , while r

travels through the domain

D , then (21.1.2'') corresponds to a continuous and twice differentiable transformation

of the domain

D into a domain ⊂

ΓD (Fig. 21.1); thus, the domain D represents

the set of the states of the mechanical system at the moment

t , every state

corresponding to a state at a point of the domain

D . In a physical (mechanical)

modelling one can imagine that the representative points are the particles of a fictitious

Other Considerations on Analytical Methods in Dynamics of Discrete Mechanical Systems

337

fluid which occupies the domain

D at the moment

t and the domain D at the

moment

t .

The transformation (21.1.2) is one-to-one and bicontinuous (hence topological), so

that a point of

D passes at a point of D , while any point of D is the image of only

one point of

D ; hence, the transformation (21.1.1) preserves the individuality of the

points, as well as the domain

D as a material variety. Indeed, the domain D is formed

only of the points which have been in

D at the initial moment. In general, the

transformation (21.1.1) conserves any material variety: curves (linear varieties),

surfaces (two-dimensional varieties) etc.

Let us consider an integrable function

= r(;)FFt of class

C definite on the set of

possible states

D of the system at the moment t . We say that the quantity

=δ

∫

(;)

IFtV

(21.1.3)

where the element of volume

δ=δδδ

2122

...

Vxxx (we use the operator δ because we

calculate for a fixed

t ) is an integral invariant of the system (21.1.1) if

(δ = δ δ δ

0000

2122

... )

Vxxx

δ= δ

∫∫

(;) ( ;)

FtV F tV

(21.1.3')

for any moment

; in this case,

is an invariant of the transformation (21.1.2). In

general, the integral

I depends on t (directly, through the agency of r and of D );

hence, it is necessary that

d/d 0

It.

Let be a curve of possible states of the system at the moment

t and the form of first

degree

=δ

∑

Fxω ,

definite on

Γ ; one obtains an integral invariant

∫

ω if

∫

ΓΓ

ωω.

(21.1.4)

One can make an analogous statement for a surface of simultaneous states.

Let be a

m -dimensional manifold

V and let be

=()δ

∑

∫

;

IFtV,

(21.1.5)

MECHANICAL SYSTEMS, CLASSICAL MODELS

338

where δ=δδ δ

...

ii i

Vxxx, the indices

, ,...,

ii i taking all the values from

1to2s , while the index k (which specifies the volume element) takes all the values

from

1to

NC (the number of volume elements);

I is an integral invariant if

()δ = ( )δ

∑∑

∫∫

;;

FtV F tV

(21.1.5')

at any moment

t .

In general, let be a

m -chain

, 1 2

Vms≤≤

, of possible states at the moment t ;

if one gives the form

=δ∧δ∧∧δ

∑

(;) ...

ii i

Ftx x xω

, defined on

V ,

where the indices

, ,...,

ii i take all the values from 1to2s , the sum having

terms and where we have introduce the exterior product (see App., Subsec. 1.2.1), then

we say that the quantity

∫

ω is an integral invariant if (

V is the m -chain of states

at the initial moment, from which result, by trajectories, the states of

V )

∫∫

ωω.

(21.1.4')

The order of the invariant is specified by the degree of the form. The integral invariant

is called absolute (denoted by

I ) if

V is an open set or relative (denoted by

I ) if

V is a closed set (with frontier). Using Stokes’s theorems, we notice that

II ;

(21.1.6)

one can state

Theorem 21.1.1 A relative invariant of order

m is equivalent to an absolute invariant

of order

+ 1m .

Thus, in case of a relative invariant of first order we have (see. App. Subsec.2.3.2)

∂

⎛⎞

δ= − δδ

⎜⎟

δδ

⎝⎠

∑∑

∫∫

1,1

kk k

kjk

Fx xx

(21.1.6')

where

is a surface which leans upon a closed curve

∂

If we replace the initial values by (21.1.2

) in (21.1.3'), then we get an invariant of

the form

∫

r(;)tVΦ

the integrand of which depends on the system of the chosen initial values; observing

that these values can vary arbitrarily, we can state

Other Considerations on Analytical Methods in Dynamics of Discrete Mechanical Systems

339

Theorem 21.1.2 A differential system of the form (21.1.1) has an arbitrary number of

integral invariants.

21.1.1.2 Complete Absolute Integral Invariants

Let be an infinitesimal domain

D , neighbouring the domain

D , both arbitrary; in

this case,

()δ = ( )δ

∑∑

;;

FtV F tV.

(21.1.7)

Let us denote the differential form in (21.1.7), called “the element of the invariant”, by

δrr(;; )Ft . Making the substitution (21.1.2

) in the second member of this relation,

that one becomes a functions of

r and t and δr , let be Φ ; we have

δ= δrr rr

(;; ) (;; ;d)Ft t tΦ .

(21.1.8)

Taking into account how the function

Φ has been built up, we notice that its numerical

value depends only on the initial values

and δr

and does not depend on the chosen

point (

r;t ) on the actual trajectory and nor on the point ( +δ +δrr;tt) chosen on the

neighbouring infinitesimal trajectory. Hence,

Φ is an invariant form, more general that

the invariant from which we started, because we are no more obliged to consider only

the simultaneous points.

If we assume that

= constt in the relations (21.1.2'''), then we must have

δ= δrr rr

(;; ;0) (;; )tFtΦ ;

(21.1.9)

t is variable, then it will intervene by δt in the calculation of δ

x . The last

differential is the total differential of a first integral, hence it can be expressed by a

linear combination of the forms

δ=δ

xxt; the quantity (21.1.9) becomes

δδ= δ−δ(;; ;) (;; )

ii iii

xt x t Fxt x XtΦ .

(21.1.9')

In this case, the absolute integral invariant (21.1.5), which is obtained by replacing

δ−δ

xxt, is called complete absolute integral invariant. But we must notice that

the methodology to obtain complete invariants can be applied only to absolute

invariants; indeed, in case of relative invariants, the invariance of the differential form

(21.1.7) under the integral does not result from the invariance of the integral (21.1.5).

21.1.1.3 The Absolute Invariant of Order

2s . Liouville’s Theorem

We notice that (21.1.3) is an integral invariant if the condition

δ=

∫

(;) 0

FtV

(21.1.10)

MECHANICAL SYSTEMS, CLASSICAL MODELS

340

is fulfilled. To reach a domain

D which does not depend on time we effect the

transformation (21.1.2'), obtaining thus

()

δ= δ= + δ

∫∫ ∫

rrr

222

dd dd

(;) ( ;);

dd dd

sss

FtV F ttJV JF V

tt tt

DD D

We observe that the derivative d/dJtof the functional determinant can be written

as a sum of

2s determinants =, 1,2,...,2

Ii s, where

I is obtained from J by

differentiating the line

i ; it results (we take into account (21.1.1))

()

−+

⎡⎤

∂

⎢⎥

∂

⎣⎦

12 1 1 2

00 0

12 2

, ,..., , , ,...,

det

, ,...,

iis

xx x XX X

xx x

Because

∂

∂∂

∂

∂∂

∑

iik

we see that

I can be calculated as a sum of 2s determinants, each one having two

identical lines, excepting that determinant which corresponds to

=ki; this determinant

is equal to

δδ/

JX x. Finally,

∂

∑

div

(21.1.11)

where

X is the 2s -dimensional vector of components

12 2

, ,...,

XX X .

Returning to the actual variables, it results

()

dd d

si i

ii i

FJV F V

ttx tx

FVF FXV

txtx x

∂∂

⎛⎞⎛⎞

=+ δ=+ δ

⎜⎟⎜⎟

∂∂

⎝⎠⎝⎠

∂

∂∂ ∂

⎡⎤⎡⎤

⎛⎞

=+ + δ=+ δ

⎜⎟

⎢⎥⎢⎥

∂∂ ∂ ∂

⎝⎠

⎣⎦⎣⎦

∑∑

∫∫

∑∑

∫∫



Because

F is a function of class

C and the domain D is arbitrary, we can state

Theorem 21.1.3

I is an invariant integral if the necessary and sufficient condition

()

∂

∑

FFX



(21.1.12)

is fulfilled.

Taking into account the results in Sect. 15.1.1.4 (formula 15.1.29)), it results that

must be a Jacobi multiplier of the system of equations (21.1.1).

Other Considerations on Analytical Methods in Dynamics of Discrete Mechanical Systems

341

= 1F , then the condition (21.1.12) becomes a condition of null divergence

∂

∑

(21.1.13)

verified by non-divergent systems; in this case

=δδ δ

∫

2122

...

xx x

(21.1.13')

is an absolute integral invariant of this system. As well,

(21.1.13'')

As we have seen in Sect. 19.1.1.6, the condition (21.1.13) is verified in case of

Hamilton’s system of canonical equations, so that the quantity

=δδ δδδ δ

∫

21212

... ...

qq qpp p

(21.1.14)

which represents the volume of the domain

D in the phase space (the phase space is

not a metric space, because we cannot establish distances; however, we consider

volume elements which are obtained by multiplying a volume element of the space of

configurations by the corresponding volume element of the space of generalized

momenta), is an integral invariant; we can state

Theorem 21.1.4 (Liouville). The volume of a domain of possible (simultaneous) states

of a Hamiltonian system remains constants during the motion.

Let us imagine a very great number of identical actual states of a system, which

differ one from the other only by their initial states

, , 1,2,...,

qpi s

; all these states

form a statistical set. Such a set may be the set of molecules of gas in a given volume.

The volume, represented by

I in the space

Γ , is called extension of phase;

Liouville’s theorem is thus known under the denomination of conservation theorem of

extension of phase too. Thus, Liouville’s theorem plays a fundamental rôle in the

deductions of Boltzmann’s equation in the kinetic theory of gas. If we remember the

mechanical image in Sect. 21.1.1.1 (the fictitious fluid), then we can say that “the flow

in the phase space is incompressible”.

In case of a canonical system we have

= 1J at the initial moment; from (21.1.13'')

it results that

= constJ , so that = 1J at any moment t .

21.1.2 Invariants of First Order

After some results of general character, one presents the Poincaré and the

Poincaré-Cartan invariants; we mention Hwa-Chung Lee’s theorem too. A special

attention is given to the connection between the integral invariants and the differential

forms.