Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

342

21.1.2.1 General Results

The condition that the integral

=δ

∑

∫

(;)

IFtx

(21.1.15)

where

Γ is a curve of simultaneous positions, be an integral invariant of first order is

written in the form

d/d 0It . If the curve

Γ (the image of the curve Γ by the

transformation (21.1.2''')) is given parametrically in the form

=rr

()λ , then the

curve

Γ will have an equation of the form =rr()λ ; in this case (we take into account

(21.1.1))

()

∂∂

⎛⎞

δ= δ=δ =δ= δ

⎜⎟

∂∂

⎝⎠

∑

dd d

ii i

xx X

xXx

tt t x

so that

()

22 22

11 11

dd d d

ss ss

kki

ii i

ki ki

xFx F x

tt t tx

ΓΓ

== ==

∂

⎡⎤⎛⎞

=δ+δ=+δ=

⎜⎟

⎢⎥

∂

⎣⎦⎝⎠

∑∑ ∑∑

∫∫

(21.1.16)

The integrand is a continuous function and

Γ is an arbitrary curve; hence,

I is an

absolute invariant if and only if the conditions

0, 1,2,...,2 ,

ki ki

iii

FF XF k s

tx x x

∂

∂∂

⎛⎞

+=+ +==

⎜⎟

∂∂∂

⎝⎠

∑∑



(21.1.16')

hold.

In the particular case in which

Γ is a closed curve (let be the curve

C ), the curve

Γ is, as well, a closed one (the curve C ). Integrating by parts the term (for a fixed t )

∂

δ=δ

∂

∑

iii

FxFX

the condition for

I be a relative invariant reads (we take into account (21.1.16) too)

∂

⎡⎤

⎛⎞

+− δ=

⎜⎟

⎢⎥

∂∂

⎝⎠

⎣⎦

∑∑

∫

FXx



(21.1.17)

Let be

12 2

/ , 1,2,...,2 , ( , ,... ; )

Fxk s xxxt=∂ ∂ = =FFF; the conditions

(21.1.16') become

∂

∂∂ ∂ ∂ ∂

⎛⎞ ⎡⎛⎞ ⎤

⎜⎟ ⎜⎟

⎢⎥

∂∂ ∂ ∂ ∂∂

⎝⎠ ⎣⎝⎠ ⎦

∂∂∂

⎛⎞

=+ = ==

⎜⎟

∂∂∂

⎝⎠

∑

0, 1,2,...,2 ,

kkk

tx x x xx

Xks

xxxt



FFF

Other Considerations on Analytical Methods in Dynamics of Discrete Mechanical Systems

343

being verified if

=d/d 0tF , hence if =

12 2

( , ,... ; ) const

xx x tF . Hence, if F is

a first integral of the system of equations (21.1.1), then

∂

∑

∫

(21.1.18)

is an absolute integral invariant of this system. The inverse implication takes place too.

Indeed, let (21.1.18) be an absolute integral invariant of the system (21.1.1); the

condition (21.1.16') leads to

(d / d )/ 0, 1,2,...,2

tx k s∂∂==F , so that

=d/d ()tftF , ()ft being an arbitrary function. It results that −

∫

()dft tF is a

first integral of the considered system of equations. If =d/d 0tF then F is a

determined first integral.

21.1.2.2 Poincaré’s Integral Invariant

Passing to Hamilton’s system of canonical equations, we consider the integral (we

use the convention of summation of dummy indices, from

1tos )

=δ

∫

Ipq

(21.1.19)

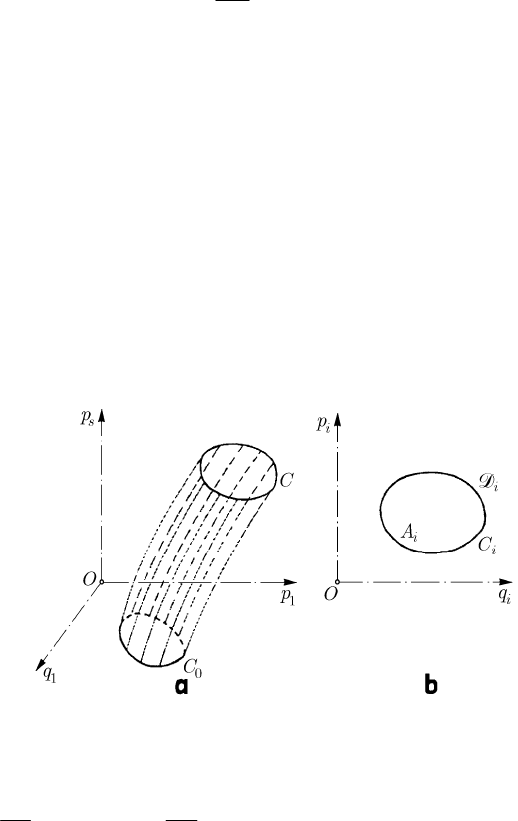
Fig. 21.2 Tube of trajectories of a fictitious fluid (a); projection of a contour on a phase plane

Considering the condition (21.1.16), we can write

()

[]

()

∂

⎛⎞

=+ δ=δ+δ−δ

⎜⎟

∂

⎝⎠

=δ − =

∫∫

∫

jjjj

kkkkk

pp q pq pq qp

pq H







along the integral curves of the canonical equations; the conditions (21.1.17) leads,

obviously, to the same result. Hence,

I is a relative integral invariant of the canonical

system (H. Poincaré’s relative integral invariant).

MECHANICAL SYSTEMS, CLASSICAL MODELS

344

This invariant integral does not change its value if the closed curve

C travels along

the tube of the trajectories of the fictitious fluid, model of the trajectories of the

representative points, starting from the contour

C , corresponding to the initial moment

t (Fig. 21.2a); these contours consist of simultaneous states. Hence,

δ= δ

∫∫

pq pq

(21.1.19')

Let be s separated phase planes ( , ), 1,2,...,

qp i s= . Projecting a contour C (from

those considered above) on one of these planes (Fig. 21.2b), we obtain the contours

, 1,2,...,

Ci s= . Projecting for each i , it results

δ= δ =±

∫∫

ii i

pq p q A

, (!),

(21.1.20)

where

A is the area of the domain

D bounded by the contour

C in the plane. The

sense of circulation on

C is specified by the sense of circulation on C ; one takes the

sign + if the sense of circulation is clockwise and the sign – otherwise. Hence,

()

=δ=±

∑

∫

ii i

Ipq A

(21.1.21)

The contours

C and

C vary during the motion (as well, the areas

A ), the algebraic

sum (21.1.21) remaining constant; this is the geometric interpretation of Poincaré’s

integral invariance.

Let be the system of differential equations

===( , ; ), ( , ; ), 1,2,...,

jj jj

qQqptpPqptj s ,

(21.1.22)

where

≡≡

12 1 2

{ , ,..., }, { , ,..., }

qqq qppp p; we calculate

()

[]

()

=δ+δ=δ+δ

=δ+δ−δ=δ−δ

∫∫

ii i i ii ii

ii ii ii ii ii

pq p q pq pq

pq pq qp Pq Qp



Equating to zero, it follows that the integral must be an exact differential

−δ (, ;)Hqpt

(because

= constt ); hence

∂∂

=− = =

∂∂

,,1,2,...

PQis

(21.1.22')

We can state

Theorem 21.1.5 If the system of differential equations (21.1.22) admits the relative

invariant (21.1.19), then it is a canonical system.

Other Considerations on Analytical Methods in Dynamics of Discrete Mechanical Systems

345

21.1.2.3 Universal Integral Invariants. Hwa-Chung Lee’s Theorem

Applying Stokes’s formula (see App., Subsec. 2.3.2), the integral

I can be written

in the form (

II )

=δδ

∫

pqI .

(21.1.23)

Let

( , ; ), ( , ; ), 1,2,...,

ii ii

QQqptPPqpti s===, be new canonical variables and

12 12

( , ; ), { , ,..., }, { , ,..., }

HHQPtQ QQ Q P PP P=≡ ≡, the corresponding func-

tion of Hamilton; if

and

are integration constants (e.g., initial values of the variables

Q and P ) in the new system, then these relations can be seen as relations of canonical

transformations.

Let use consider, in the phase space

(, )qp , a two-dimensional variety

V , which is

transformed in the two-dimensional manifold

′

V . By means of two parameters (u and v ),

we can thus express the canonical co-ordinates in the form

= (,)

qquv, = (,)

ppuv,

=,1,2,...,

In this case, we can write

()

[]

∂

⎡⎤

δδ = δδ

⎢⎥

∂

⎣⎦

∂∂ ∂∂

⎛⎞

=−δδ=δδ

⎜⎟

∂∂ ∂∂

⎝⎠

∫∫

det

kk kk

qp uv

qp qp

uv uv uv

uv vu

Ω

ΩΩ

where

[,]uv is Lagrange’s bracket and Ω is the domain on which one integrates in the

plane of variables

u and v ; as well, we have

()

[]

′

∂

⎡⎤

δδ = δδ= δδ

⎢⎥

∂

⎣⎦

∫∫ ∫

det ,

Q P uv uv uv

ΩΩ

where we have used the invariance of Lagrange’s bracket to a canonical transformation

(see Sect. 20.2.2.3). We obtain thus the identity

′

δδ = δ δ

∫∫

qp QP;

(21.1.23')

we can state that

I is an absolute integral invariant of second order of the canonical

system or of the canonical transformation.

Analogously, we can define integral invariants of higher order, that is the relative

integral invariant

−

=δδδδδδ

∑

∫

1122

...

iiii ii

Ipqpqpq

(21.1.24)

and the absolute integral invariant

=δδδδδδ

∑

∫

1122

...

iiii ii

pqpq pqI

(21.1.24')

MECHANICAL SYSTEMS, CLASSICAL MODELS

346

where the indices

, ,...,

ii i

take all the values from

1tos

, so that the sums contain

C terms; these invariants are defined on manifolds of odd or even number of

dimensions, respectively, Using theorems of Stokes type, one can show that

−

21 2ll

I I .

(21.1.24'')

On the same way as in the case

= 2l , using a relation of the form

()

∂∂∂

⎡⎤ ⎡⎤

⎡⎤

⎢⎥ ⎢⎥

⎢⎥

∂∂∂

⎣⎦

⎣⎦ ⎣⎦

∑

12 2 12 2 12 2

12 12 2 12

, ,..., , ,..., , ,...,

det det det

, ,..., , ,..., , ,...,

sss

l l

XX X XX X xx x

uu u xx x uu u

one can show that

d/d 0

It.

In the particular case

=ls, one obtains again the absolute integral invariant

I of

Liouville.

We notice that both

21l

−

and

, 1,2,...,

Il s= , do not depend on the structure of

Hamilton’s function

H , hence do not depend on the considered mechanical system, but

only on the canonical form of the equations; thus, these integral invariants are called

universal integral invariants. The uniqueness of these invariants has been put in

evidence, in 1947, by Hwa-Chung Lee, who made a profound study of them; in this

order of ideas, we state

Theorem 21.1.6 (Hwa-Chung Lee). If

[

]

′

=δ+δ

∫

(, ;) (, ;)

jj j

IAqptqBqptp

(21.1.25)

is a universal relative integral invariant, then

′

,constIcIc ,

(21.1.25')

where

I is the relative integral invariant of Poincaré.

We prove the theorem in the particular case

= 1s for the universal relative integral

invariant

[]

′

=δ+δ

∫

(, ;) (, ;)

IAqptqBqptp

in the phase plane

(, )qp , the closed curve C being in this plane. The solution of the

Hamiltonian system

/, /qHpp Hq=∂ ∂ =−∂ ∂



will be of the form =

(; , )qqtqp,

(; , )pptqp, with ==

000 0

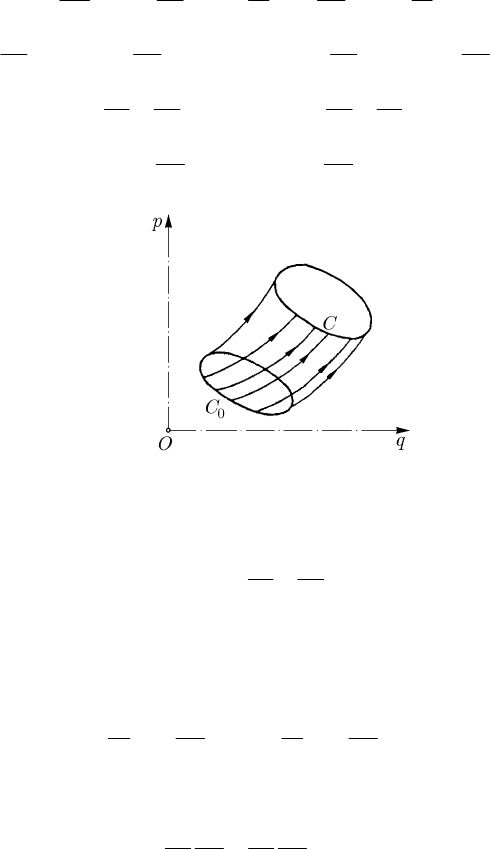
(), ()qqtppt. Let be ==

00 0 0

()and ()qq ppλλ,

000 0

0 , (0) ( ), (0) ( )lq ql p plλ≤≤ = = , the parametric equations of a closed

contour

C in the phase space (Fig. 21.3); the points of this contour reach at the

moment

t the contour C , the equations of which (after replacing the parametric

representation of

q and

p ) are given by ==≤≤(; ), (; ),0qqt ppt lλλλ.

Other Considerations on Analytical Methods in Dynamics of Discrete Mechanical Systems

347

If we replace in the integral

′

I , we obtain a function of parameter t , so that the

condition of invariance becomes

′

d/d 0It . Differentiating under the integral sign

and integrating by parts (

δ=− δ

∫∫

uv vu

), we get

{}

′

⎛⎞

=δ+δ+δ+δ

⎜⎟

⎝⎠

⎛⎞⎛⎞

=δ+δ+δ+δ=δ−δ+δ+δ

⎜⎟⎜⎟

⎝⎠⎝⎠

∂∂ ∂∂

⎡⎛ ⎞ ⎤ ⎡⎛ ⎞ ⎤

=−+δ+−+δ

⎜⎟ ⎜⎟

⎢⎥⎢⎥

∂∂ ∂∂

⎣⎝ ⎠ ⎦ ⎣⎝ ⎠ ⎦

∂∂

⎛⎞⎛

=−+δ+−+

⎜⎟

∂∂

⎝⎠⎝

∫

∫∫

∫

dddd

ddddd

dd dd

qA q pB p

ttttt

AB AB

qAq pBp qqA ppB

tt tt

AB BA

pAq qBp

pq qp

ZAqZB

 







⎡⎞⎤

δ=

⎜⎟

⎢⎥

⎣⎠⎦

∫

Fig. 21.3 Representations of the closed contours

C and C

where we took into account the canonical equations and we have denoted

∂∂

=−

∂∂

The integral thus obtained must vanish for any

t (considered as a parameter) and for an

arbitrary integration path; hence, the integrand must be a total differential with respect

to the variables

q and p , so that

∂∂ ∂∂

⎛⎞⎛⎞

−+=−+

⎜⎟⎜⎟

∂∂ ∂∂

⎝⎠⎝⎠

ZA ZB

pq qp



or (taking into account the notation made)

∂∂ ∂∂

−+ +=

∂∂ ∂∂

ZH ZH

pq qp



Because

H may be chosen arbitrarily, it results that

∂∂=∂∂==// 0Zp ZqZ



==,constZcc . We can also write

MECHANICAL SYSTEMS, CLASSICAL MODELS

348

∂−

∂

∂∂

()Acp

;

hence, there exists a function

(, ;)qptϕ (t is a parameter), so that

∂∂

−δ+δ=δ+δ=δ

∂∂

()Acp q Bp q p

ϕϕ

wherefrom

δ+ δ = + δ = δ=

∫∫∫

()()

CCC

Aq Bp cpq c pq cIϕ

vvv

the theorem being thus proved.

In the case

> 1s one uses the same ideas; but the proof is much more complicated.

One can state an analogous theorem for

> 1l .

21.1.2.4 The Poincaré-Cartan Integral Invariant

We make a study of the variation of the Lagrangian action

in the general case

in which both the generalized co-ordinates and the time depend at the initial and at the

final moments on a parameter

λ , so that

== =

=≤≤=

( ), ( ), ( ; ),

( ; ), 0 , 1,2,..., .

tt tt qqt

qqt ll s

λλ λ

λλ

(21.1.26)

The Lagrangian action will be, in this case, of the form

()

∫

()

( ) (; ), (; ); d

qt qt t t

λλλ

;

(21.1.27)

differentiating (the limits depend on a parameter) and integrating by parts, we obtain

∂∂

⎛⎞

δ=δ−δ+ δ+δ

⎜⎟

∂∂

⎝⎠

∂∂∂

⎡⎛⎞⎤

=δ−δ+ δ + − δ

⎜⎟

⎢⎥

∂∂∂

⎣⎝⎠⎦

∫

() d

iii

tt q qt

qqtq

λ 





ALL

LLL

where

((,), (,); ), 0,1

qt qt t

αααα

λλα==



LL . Along the integral curves of the

canonical system, we remain with

δδ−δ+δ−δ

() ()

tt tt

ii i i

ttpq pq

=AL L ;

(21.1.27')

Let us consider also the variations of the co-ordinates

(( ); ), 0,1

qqt

αα

λλ α==,

in the form

δ=δ+∂ ∂ = =[ ( ; )/ ] , 1,2,..., , 1,2

ii i

qqt qt i s

αα α

λλ α , so that

Other Considerations on Analytical Methods in Dynamics of Discrete Mechanical Systems

349

δ=δ−δ= =[ ] , 1,2,..., , 1,2

iii

qqqtis

αα

α ;

(21.1.28)

replacing in

, expressing the generalized velocities by means of the generalized

momenta and taking into account

−=

pq H







L (after introducing the generalized

momenta), we get (along the integral curves of the canonical system)

[]

δδ−δ=δ−δ−δ+δ

11 0 0

ii ii i i

pq Ht pq Ht pq H t

=A .

(21.1.27'')

Being situated in the space

+2112 1 2

( , ,..., , , ,..., ; )

qq qpp ptΓ , let be a closed curve

C of equations

===≤≤=

(), (), (),0 , 1,2,...,

ii i i

qq pp tt li sλλλλ

;

(21.1.29)

Fig. 21.4 Closed tube of trajectories

we put the condition to obtain the same point of the curve

C for = 0λ and = lλ . From

any point of this curve starts a unique trajectory, determined by the canonical equations and

by the initial conditions, obtaining thus a closed tube of trajectories (Fig. 21.4)

≤≤ =

(; ), (; ),

(;0) (;), (;0) (;),

0 , 1,2,..., .

ii i i

iii i

qqt ppt

qt qtl pt ptl

li s

λλ

(21.1.30)

We choose on this tube another closed curve

C which has only one common point

with every trajectory; thus, to each

λ corresponds a trajectory and only a single point

C , so that we can write the equations of the curve

C in the form

===

(), (), ()

ii i i

qq pp ttλλλ.

(21.1.30')

Integrating the relation (21.1.27'') with respect to

λ , from

0tol

, it results

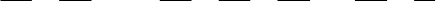
MECHANICAL SYSTEMS, CLASSICAL MODELS

350

[]

()

()()

−δ−δ

=δ−δ−δ+δ

=δ−δ−δ−δ=

∫

∫∫

11 00

(1) (0)

ii ii

pq Ht

pq Ht pq Ht

=AA

so that

()()

δ−δ= δ−δ

∫∫

ii ii

p q Ht p q Ht

;

hence, the integral

()

=δ−δ

∫

IpqHt

(21.1.31)

taken on a curve

, obtained by displacement and deformation from

, along the

tube of trajectories, remains constant in time. We obtain thus an integral invariant called

the Poincaré-Cartan integral invariant, corresponding to the system of canonical

equations. E. Cartan extended Poincaré’s integral invariant to contours of

non-simultaneous states, by introducing the supplementary term

−δHt; but if

represents a set of simultaneous states (we make

δ=0t ), we find again Poincaré’s

integral invariant.

To can prove the inverse implication, we consider a tube of trajectories which verify

the system of differential equations (21.1.22), so that – on a closed curve surrounding it

– the integral (21.1.31) is invariant; such a curve can be represented in parametric form

====(, ), (, ), 1,2,...,, (, )

ii i i

qq pp i sttλμ λμ λμ ,

(21.1.32)

where the parameter

λ is fixing the trajectory which starts from a point of the curve

C , while the parameter μ corresponds to the point on this trajectory. The system of

equations (21.1.22) reads

===== ===

12 12

dd dd

ddd

... ... ( , ; )d

qq pp

qpt

QQ Q PP P

where

(, ;)qpt

is an arbitrary function in the extended phase space

+21s

(thus, the

family of curves

= constμ

is, at the actual state, an arbitrary family of closed curves,

which are not intersecting and which surround the given tube of trajectories). To

integrate this system of equations, we can express its solution by means of functions of

μ and of the initial values

, , 1,2,...,

qp i s=

and

t (for = 0μ ) in the form

====

00 00 00

00 0

( , , ; ), ( , , ; ), 1,2,..., , ( , , ; )

ii i i

q ftq p p gtq p i st ttq pμμ μ.

Other Considerations on Analytical Methods in Dynamics of Discrete Mechanical Systems

351

One obtains thus a parametric representation of the family of integral curves of the

system (21.1.22). The initial positions of the corresponding representative point will be

on the curve

C (to obtain the considered tube), given by (21.1.29); we obtain thus the

equations (21.1.32). For any

= constμ we find a point on each generating trajectory

and a corresponding closed curve (with

≤≤0 lλ ). The integral I becomes a function

μ ; imposing the condition that I be an invariant by passing from a curve C to

another closed curve along the tube, we write

=d0I (we differentiate with respect to

μ ). Differentiating with respect to μ under the integral sign, it results

[]

δ+ δ− δ+ δ =

∫

dd(dd)0

ii i i

pq p q Ht H t

;

by permutation of the operators

δdand

(the first one represents the differentiation

with respect to

μ , while the second one represents the differentiation with respect to

λ ) and integrating by parts, we obtain (the integrated term vanishes on a closed

contour)

()

δ−δ − δ+δ

∂∂

⎡⎛ ⎞ ⎛ ⎞ ⎤

=+δ+−+δ+−+δ=

⎜⎟⎜ ⎟

⎢⎥

∂∂

⎣⎝ ⎠ ⎝ ⎠ ⎦

∫

dddd

d0,

ii ii

iiii

pq pq Ht Ht

HHH

pqqp Ht

qpt





because

∂∂

δ= δ+ δ+δ

∂∂

HqpHt



Taking into account (21.1.22), we obtain

()

∂∂

⎡⎛ ⎞ ⎛ ⎞ ⎤

+δ+−+δ+−+δ =

⎜⎟⎜ ⎟

⎢⎥

∂∂

⎣⎝ ⎠ ⎝ ⎠ ⎦

∫

iiii

HHH

PqQp Ht

qpt



;

the integrand must be an exact differential with the arbitrary factor

, which is

possible only if the brackets vanish, being thus led to the equations (21.1.22') (we

obtain also

=d/dHtH



, result which is – in fact – a consequence of the canonical

equations). We can thus state

Theorem 21.1.7 If the system of differential equations (21.1.22) admits the relative

invariant (21.1.31), then this system is canonical.

Hence, the Poincaré-Cartan integral invariant can be stated at the basis of

Hamiltonian mechanics, because it leads us to the canonical equations.

We notice that in this integral invariant the time plays the rôle of a co-ordinate and

−H (the mechanical energy with changed sign) plays the rôle of a generalized

momentum; the mentioned analogy is particularly useful.

Indeed, introducing the new function

=− (, ;)zHqpt, we can calculate

=−

112 23

( , ,..., , , , ,..., ; )

pKqqqzpppt, so that the integral (21.1.31) becomes