Teodorescu P.P. Mechanical Systems, Classical Models Volume II: Mechanics of Discrete and Continuous Systems

Подождите немного. Документ загружается.

()

IMR MR FRωλω+=+ =+



M ,

λ =

whence, by integration,

()

ωω

()

vv t

MRλ

′′

(14.2.57)

The force of sliding friction will be given by

273

14 Dynamics of the Rigid Solid

()

−

(14.2.58)

Imposing the condition

()

fN f G F≤= −T , we find

FRλ − M

()

1 fG F Rλ≤+ − , so that the condition of rolling without sliding becomes

−≤≤+

′′′ ′′′

MM MMM,

FRλ=

′

M ,

()

1 fG F Rλ=+ −

′′

M .

(14.2.59)

0FR+>M , then the quantities ω and

′

are always positive, while the angular

velocity

ω (hence, the velocity

′

too) grows indefinitely, in direct proportion to time;

in case of equality (

0FR+=M ), the velocities ω and

′

remain constant during

the motion. If

0FR+<M , then the rolling takes place with an angular velocity

which diminishes in direct proportion to time till the moment

()

1/tMRFRλω=− + +M

, when 0ω = and 0

′

= ; for tt> one obtains

a rolling in the opposite sense (

0ω < ), where

MM=+M is taken (because the

moment of rolling friction is opposed to the motion). If

MMFRM−≤ + ≤ and

0ω = , then the cylinder remains at rest.

In the case in which one of the relations

<−

′′′

MM M

′′′

MM M

(14.2.60)

takes place, we must assume that

()

fN f G F== −T , having to do with a rolling

without sliding; in this case, the equations (14.2.54), (14.2.54') lead to

()

vv FTt

′′

=+ − ,

()

ωω=+ +M .

(14.2.61)

We suppose that

′

= at the initial moment; but at a moment t takes place the

relation (14.2.53'). We obtain thus the relation (we notice that we have a relation of the

form (14.2.53) at the initial moment)

()

′

=−+

′′′

∓MM M

(14.2.62)

where we have used the relations introduced above; the double sign corresponds to the

sense of the force of sliding friction

T, obtaining thus 0

′

> or 0

′

< , as the sign −

(for

T in a sense opposite to the motion, as in Fig. 14.22) or the sign

+ is taken,

respectively. Hence, if the first relation (14.2.60) is taken, then the motion involves a

sliding of velocity

′

> on the

′′

-axis, while – in case of the second relation

(14.2.60) – the sliding velocity is

′

< .

274

MECHANICAL SYSTEMS, CLASSICAL MODELS

′

≠ , then the relation (14.2.53') takes place at the initial moment too. Because

′

is a function continuous in time, it must have the same sign as

′

, at least for small

values of t. On the same way, we can write

()

for 0,

for 0.

vtv

⎧

′′

+−+− >

⎪

′

⎨

⎪

′′

+−++ <

⎩

′′′

MM M

(14.2.62')

Firstly, let us suppose that

′

> . If ≤−

′′′

MM M

, then we have, 0

′

> for

any time, while if

>−

′′′

MM M

, then 0

′

> at the initial moment and it is

diminishing and then vanishing for

/( )

tmRv

′

=−+

′′′

MM M; thus, we come

back to the case considered before (

′

), taking the moment tt= as initial

moment. Let be now

′

< . If

≥+

′′′

MM M

, then 0

′

< at any moment t,

while if

′′′

MM M, then 0

′

< at the initial moment and then increases till

vanishing for

/( )

tmRv

′

=− + −

′′′

MM M

; we return thus to the case

′

Finally, if

−≤≤+

′′′ ′′′

MM MMM, then takes place firstly a rolling with

sliding and then a rolling without sliding, while if

′′′

MM M

<−

′′′

MM M, then a phenomenon of rolling with sliding takes place for any time.

In the first of these cases, the sliding velocity

′

vanishes at the moment tt= , while

the force of sliding friction has no more the absolute value fN but it is given by

(14.2.58), which leads to discontinuities both for T and for the derivatives

d/d

′

and



in the equations (14.2.54), (14.2.54'); but the velocities

′

and ω remain

continuous functions. These results can be put in connection with the study

corresponding to the drawn and motive wheel (see Chap. 4, Sect. 2.1.4).

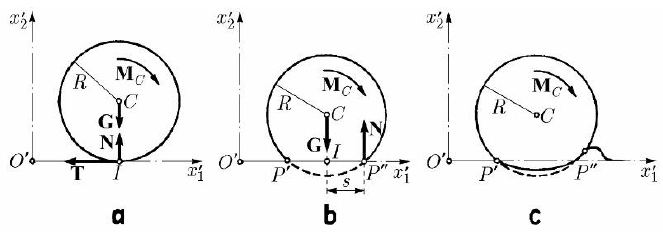
In our study, we have assumed till now that the disc reaches the horizontal plane at

only one point I. In this case, under the action of a moment

M and of a tangential

force

T, we obtain the equations of motion (Fig. 14.23a)

′

=−

IMTRω =+



(14.2.63)

Taking into account the relation

vRω

′

corresponding to the phenomenon of rolling

(without sliding) and eliminating the force of sliding friction T, we obtain

()

IMR MR Mωλω+=+ =



(14.2.63')

which shows that the disc begins to roll for any

M > (having 0ω >



too). In

reality, the disc cannot remain perfectly rigid; it is deformed, the contact with the

horizontal plane taking place on the segment

′′′

(Fig. 14.23b). Taking into account

275

14 Dynamics of the Rigid Solid

the sense of rolling of the disc, that one will effect – in fact – a motion of rotation about

the point

′′

, being detached from the point P

′

; we can thus assume that the normal

constraint force

N is applied at the point P

′′

, at a distance s from the support of the

own weight

G, the equation of motion being written in the form

IMTRsNω =+−



, (14.2.64)

so that

()

IMR MR MsNωλω+=+ =−=



M .

(14.2.64')

Hence, for a phenomenon of rolling it is necessary that

MsNM>=. We must

mention that, in reality, the horizontal plane is also deformed, so that – locally – the

contact zone is as in the Fig. 14.23c.

By a powercraft we mean a vehicle which is displaced by the rolling of its wheels,

put in motion by a motor (of any nature), e.g., automobile, locomotive, street motorcar,

motorcycle etc.

We, firstly, consider the departure of a powercraft (the starting, the departure from a

state of rest) with respect to an inertial frame of reference. We point our attention on a

motive wheel, assuming that it is acted upon by a driving torque of moment

M and

that a rolling moment

M arises too; we assume also that

0FF== (we use the

14.2.2.8 Departure and Stopping of a Powercraft

Fig. 14.23 Rolling of a rigid and of a non-rigid disc on a horizontal plane

notations in the previous subsection). At the initial moment, when the wheel is at rest,

we have

0ω =

′′

==. The formulae (14.2.59) lead to

′

M ,

()

1 fGRλ=+

′′

M .

(14.2.65)

To can put the wheel in motion, we must have

MM=−>M .

≤

′′

MM, then the wheel begins to roll without sliding, and the motion can

continue till infinity; the angular velocity

ω grows in direct proportion to time. From the

276

MECHANICAL SYSTEMS, CLASSICAL MODELS

second formula (14.2.57) it results that in an interval of time given by

(1 ) /tMRVλ=+ M the powercraft reaches the velocity V; thus, it results

(1 )

MRV

λ=+M ,

(14.2.66)

hence, the moment

M of the driving couple necessary to reach the velocity V in an

interval of time equal to

t . Taking into account (14.2.65), (14.2.66), the condition

≤

′′

MM takes the form

Vft

≤

(14.2.67)

obtaining thus a limitation of the velocity V function of the time

t ; we notice that G is

the part of the whole weight of the powercraft which corresponds to the axle of the

wheel, M being the mass of it.

The kinetic energy of the wheel at the moment

t will be (we have /VRω = ,

()

tωω= )

()

2222

11 1 1

22 2

TMV I IMRV MV

ωλ=+= + =+,

while the kinetic energy consumed by rolling friction is calculated in the form (we use

the first formula (14.2.57) and the formula (14.2.66))

()

tsG MV

TMtsG

== =

∫

Thus, the kinetic energy consumed by the powercraft to reach the velocity V is given

()

TTT MV

λ=+ = + +

(14.2.68)

′′

, then the rolling will be accompanied by sliding and the wheel will

slip. Obviously, in this case the kinetic energy necessary to reach the velocity V in an

interval of time

t will be greater. To avoid this loss of kinetic energy it is necessary

that the inequality

≤

′′

takes place; in this order of ideas, from the relations

(14.2.66) and (14.2.67) we obtain

(1 )fGRλ≤+M .

(14.2.69)

277

14 Dynamics of the Rigid Solid

Assuming that the moment

M of the driving couple is realized by a force F applied

tangentially at the peripheral of the wheel (

MFR= ) and observing that

tan

MsGGRα== we can also write (

MM=−M )

()

[]

tan 1FfGαλ≤++.

(14.2.70)

Neglecting the angle of rolling

α (e.g., in case of a locomotive), it results

()

1FfGλ≤+ , (14.2.70')

a formula particularly useful in applications.

Analogously, one can make a study of the stopping of the powercraft by braking the

wheels; in this case, we must have

MRψ=− < , where

0ψ >

is a coefficient of

the nature of a length, which corresponds to the brake slipper friction on the peripheral

of the wheel. We notice that

′

= ,

/VRω = ,

′

= ,

0F = , hence

′

>−

′′

, then we have a rolling without sliding; the time

t necessary to

make vanishing the velocity V by deceleration will be given by the second formula

(14.2.57) in the form (we have

tan

MsNsGGRα=== )

(1 ) (1 ) (1 )

tan

MRV MRV MV

RM G

λλ λ

ψψα

=− + = + = +

(14.2.71)

<−

′′

MM, then the powercraft will stop by the rolling with sliding of the

wheels; the formulae (14.2.61) lead to (we have put

TfNfG==)

vV fGt

′

=− ,

()

fGR t

ωω=+ +M ,

ω =

In this case,

()

tan

IIV

fGR R fGR

ψα

′

=− =− =

′′

(14.2.72)

represents the interval of time after which the linear velocity

′

and the angular

velocity

ω, respectively, vanish; it results

(1 )fGR

fGR

λ++

′′ ′

−=

(14.2.72')

As in the case of the departure of the powercrafts, the moment M

′′

is given by

(14.2.65); from

0+<

′′

we obtain (1 ) 0fGR fGRλ+<++ <MM , so that

′′ ′

. Hence, after an interval of time

′

, the wheel is slipping (it does no more

rotate) with the velocity

′′

= till the moment t

′′

when 0

′′

==, and the

powercrafts stops.

278

MECHANICAL SYSTEMS, CLASSICAL MODELS

If we use simplified models (the modelling as particles), for the powercraft and for

the wheel in the interval of time

′′

in which the wheel is slipping and if GMg=

(corresponding to the powercraft), we can write (

′

= , assuming a null peripheral

mass, hence

0λ = )

′′

(14.2.73)

The distance l travelled through in this interval of time will, obviously, be given by

(14.2.73')

hence a formula of the Torricelli type. Taking

9.806 m/sg =

and assuming a

Table 14.1

30 40 50 60 70 80 90 100

0.3 11.80 20.98 32.79 47.21 64.26 83.93 106.22 131.14

0.6 5.90 10.49 16.39 23.61 32.13 41.97 53.11 65.57

coefficient of friction

0.3f =

for a wet ground and a coefficient of friction

0.6f =

for a dry ground, we give in Table 14.1 the braking distance l in m for various values

of the velocity V in km/h.

Chapter 15

Dynamics of the Rigid Solid with a Fixed Point

The frictionless motion of a rigid solid about a point of it, fixed with respect to an

inertial (fixed) frame of reference, is one of the basic problems in the motion of a rigid

solid, important from a theoretical point of view (as an intermediary phase in the

solution of other problems or as a problem in itself), as well as from the point of view

of practical applications. This problem has been considered for the first time in 1749 by

d’Alembert, but the final form of the equations of motion has been given by L. Euler in

1758. Subsequent researches are due to J.-L. Lagrange, L. Poinsot, S.-D. Poisson,

C.G.J. Jacobi, Ch. Hermite and Sonya Kovalevsky. Further, many other studies have

been made, which are continuing also now.

After a general study of the motion of a rigid solid with a fixed point, one considers

the most important cases of integrability of the corresponding system of differential

equations.

15.1 General Results. Euler-Poinsot Case

Using the general results which are presented, one considers the Euler-Poinsot case of

integrability, interesting both in the study of the heavy rigid solid and in the study of

other cases of loading; thus, various analytical and geometric aspects of the problem are

developed.

15.1.1 General Results

In what follows, one makes firstly some preliminary considerations; general methods of

computation are then presented, using the theory of the last multiplier, as well as the

most important cases of integrability.

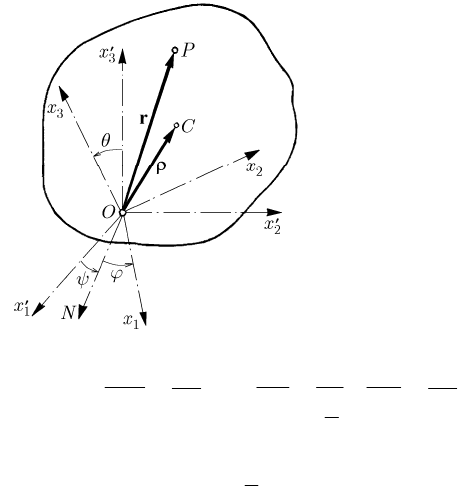
15.1.1.1 Kinematical Considerations

Fixing one of the points of the rigid solid

S, the number of degrees of freedom of it is

reduced to three, corresponding to the three components of the rotation vector applied

at the fixed point. Obviously, this point is chosen as pole

′

of the inertial frame of

reference

′

; as well, without any loss of generality, the pole O of the non-inertial

frames

R and R can be situated at the same point OO

′

≡ (hence,

′

=r0

), so that

≡

′

(the frame R being inertial too).

The position of the frame of reference

R (hence, of the rigid solid) with respect to

the frame

′

is specified by Euler’s angles: ()tψψ= , 02ψπ≤< , ()tθθ= ,

P.P. Teodorescu, Mechanical Systems, Classical Models,

279

MECHANICAL SYSTEMS, CLASSICAL MODELS

0 θπ≤≤, and ()tϕϕ= , 02ϕπ≤< (Fig. 15.1); as a matter of fact, these angles

can be considered as components of the rotation of the rigid solid about the fixed point.

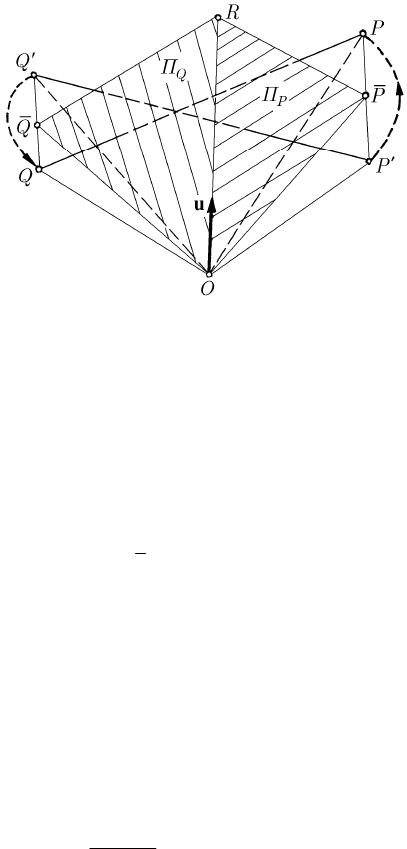
Indeed, be PQ a segment of a line which belongs to the rigid solid, situated in the

position

′′

with respect to the frame

′

, at the initial moment at which the frame

R coincides with the frame

′

; after the motion of the rigid solid about the fixed

point, the frame

R reaches the actual position, while the segment of a line PQ has

another position with respect to the frame

′

, but the same position with respect to

Fig. 15.1 The fixed and movable frames of reference. Euler’s angles

the frame

R. Obviously, we have PQ PQ

′′

and OP OP

′

= , OQ OQ

′

. The

plane

Π , normal to the segment of a line PP

′

at its middle

, passes through the

point

O, being a plane of symmetry for the isosceles triangle POP

′

; the plane

Π ,

normal to the segment of a line

′

at its middle Q , has the same property. The

intersection of the two planes is a line

OR (Fig. 15.2). Because of symmetry reasons

with respect to the plane

Π , we have



POR POR

′

= ; analogously, we can write



Q OR QOR

′

= . But, by means of the considered motion, the point P

′

reaches the

point

P, while Q

′

reaches the point Q, the angles



POR

′

and



QOR

′

remaining

invariant; the straight line

OR remains fixed with respect to the frame

′

during the

motion, so that it is an axis of rotation. We find thus again Euler’s Theorem 14.1.1,

which can be applied in the case of a finite rotation, as well as in the case of an

instantaneous one.

Hence, one passes from the frame of reference

′

to the frame R by a rotation of

angle χ about an axis of unit vector u; this motion can be represented in various forms

(see Sects. 14.1.1.1-14.1.1.3). Denoting

′′





and OP =





and using the results in

Sect. 14.1.1.1, we can write (see Fig.14.3 too)

280

15 Dynamics of the Rigid Solid with a Fixed Point

cos ( )(1 cos ) sinχχχ

′′ ′

=+⋅−+×

rr ru uur .

(15.1.1)

Fig. 15.2 Passing from the frame of reference

′

R to the frame R

Projecting on the axes of the frame

′

, we obtain the transformation matrix α of

components (

′

rrα ,

iijj

xxα

′

ij i j

′

=⋅

ii, ,1,2,3ij= )

cos (1 cos ) sin

ij ij i j

ijk k

uu uαδ χ χ χ=+−−∈ , ,1,2,3ij= .

(15.1.1')

Calculating the trace of this tensor, the rotation angle χ will be given by (

uu = )

()

cos 1

χα=−,

(15.1.2)

corresponding to the considerations in Sect. 14.1.1.1. Noting that

kjkll

×=∈ii i,

,1,2,3jk= , and projecting on the axes of the frame

′

, it results

ijk mk lmn li

αα α∈=∈

,, 1,2,3imn= . Taking into account the relation

ik jk

αα δ= ,

,1,2,3jk=

, too, we get

[][]

232

kk ll

kjk

αα α α α−=− , wherefrom

()

1/4 1

α −≤; the formula (15.1.2) leads thus always to acceptable values for the

angle

χ. Considering the antisymmetric part of the tensor (15.1.1'), we obtain,

analogously,

2sin

ijk jk

∈

=−

, 1, 2, 3i = .

(15.1.2')

Hence,

sin χ−u is the vector associated to the antisymmetric part of the tensor α.

Knowing the matrix α, we can determine the rotation of angle

χ about the axis of unit

vector u; as we have seen in Sect. 14.1.1.2, this representation is multiform. Even if we

restrict ourselves to the interval

[

]

0,2π , the relation (15.1.2) leads to the values χ and

2πχ− (distinct values, excepting the particular case χπ= ); from (15.1.2') one

281

MECHANICAL SYSTEMS, CLASSICAL MODELS

obtains the components

u and

u− , respectively, in fact the same rotation otherwise

represented.

Denoting

sin

λ = ,

sin

μ = ,

sin

ν = , cos

ρ =

(15.1.3)

we find again the representation (14.1.6) of the matrix α.

The rotation velocity of the movable frame of reference

R, rigidly linked to the

solid, with respect to the fixed frame

′

, is characterized by the angular velocity

vector

()t=ωω, which is expressed, by means of Euler’s angles ψ, θ, ϕ, in the vector

form (5.2.34) and, in components, in the form (5.2.35), with respect to the frame

R, or

in the form (5.2.35'), with respect to the frame

′

; we mention also the inverse

relations (14.1.15) and (14.1.15'), respectively (see Sect. 14.1.1.4 and Fig. 14.1 too).

Introducing the functions

()

tαα= , 1, 2, 3i = , which represent the direction cosines

of the

′

-axis with respect to the movable frame R, we obtain the relations (5.2.36)

and (14.1.16). The functions

α and

ω are linked by the differential relations (5.2.37')

(see Chap. 5, Sect. 2.3.3). The accelerations distribution will be of the form (5.2.38),

the fixed point being the only one of null acceleration. We remark also that the motion

is reduced to a finite rotation if and only if the vectors



ω and ω are collinear or if



0ω . Noting that

ωωω= , we get

2222

2cosωψθϕ ψϕθ=+++





(15.1.4)

The fixed and movable axoids are two tangent cones, with the vertices at the fixed

point (Poinsot’s cones); the motion of the rigid solid with a fixed point will be thus

characterized by the rolling without sliding of the polhodic (movable) cone

C over the

herpolhodic (fixed) cone

C (see Fig. 5.16 too). Let

ω ,

1,2, 3i =

, be the components of

the vector ω in the frame of reference

R ; an arbitrary point P on the support of the vector

ω has the co-ordinates

x λω= , 1, 2, 3i = , λ scalar, with respect to this frame.

Replacing in the relations (5.2.35) and eliminating the parameter

λ and the time t

between these three relations, we obtain the equation of the polhodic cone with respect

to the non-inertial (movable) frame

R. Analogously, we denote by

′

, 1,2, 3i = , the

components of the same vector ω with respect to the frame

′

; the point P will have

the co-ordinates

x λω

′′

= , 1, 2, 3i = . We replace then in the relations (5.2.35') and

eliminate the parameter

λ and the time t between these three relations; we get thus the

equation of the herpolhodic cone with respect to the inertial (fixed) frame

′

The points of the rigid solid which are situated on a sphere of centre

O form a

spherical figure

F, of invariable form, movable on this sphere. The traces of the cones

C and

C of vertex O on this sphere are two curves: the curve

C , fixed on the

282