Tarek Ahmed. Reservoir engineering handbook

Подождите немного. Документ загружается.

where k

= vertical permeability

= horizontal permeability

Allard and Chen (1988) pointed out that there are an infinite number

of solutions to Equation 10-28, representing all possible reservoir-aquifer

configurations. They suggested that it is possible to derive a general solu-

tion that is applicable to a variety of systems by the solution to Equation

10-28 in terms of the dimensionless time t

, dimensionless radius r

, and

a newly introduced dimensionless variable z

where z

= dimensionless vertical distance

h = aquifer thickness, ft

Allen and Chen used a numerical model to solve Equation 10-28. The

authors developed a solution to the bottom-water influx that is compara-

ble in form with that of van Everdingen and Hurst.

= B ∆p W

(10 - 31)

They defined the water influx constant B identical to that of Equation

10-21, or

B = 1.119 φ c

h(10-32)

Notice that the water influx constant B does not include the encroach-

ment angle θ.

The actual values of W

are different from those of the van Everdin-

gen-Hurst model because W

for the bottom-water drive is also a func-

tion of the vertical permeability. Allard and Chen tabulated the values of

as a function of r

, t

, and z

. These values are presented in Tables

10-3 through 10-7.

The solution procedure of a bottom-water influx problem is identical

to the edge-water influx problem outlined in Example 10-7. Allard and

Chen illustrated results of their method in the following example.

= (10 - 30)

678 Reservoir Engineering Handbook

Reservoir Eng Hndbk Ch 10 2001-10-25 14:22 Page 678

Example 10-8

An infinite-acting bottom-water aquifer is characterized by the follow-

ing properties:

=∞ k

= 50 md F

= 0.04

φ=0.1 µ

= 0.395 cp c

= 8 × 10

−6

psi

−1

h = 200′ r

= 2000′  = 360°

The boundary pressure history is given below:

Time, days p, psi

0 3000

30 2956

60 2917

90 2877

120 2844

150 2811

180 2791

210 2773

240 2755

Calculate the cumulative water influx as a function of time by using

the bottom-water-drive solution and compare with the edge-water-drive

approach.

Solution

Step 1. For an infinite-acting aquifer:

=∞

Step 2. Calculate z

from Equation 10-30.

Step 3. Calculate the water influx constant B.

B = 1.119 (0.1) (200) (8 × 10

−6

) (2000)

= 716 bbl/psi

200

2000 0 04

Water Influx 679

(text continued on page 702)

Reservoir Eng Hndbk Ch 10 2001-10-25 14:22 Page 679

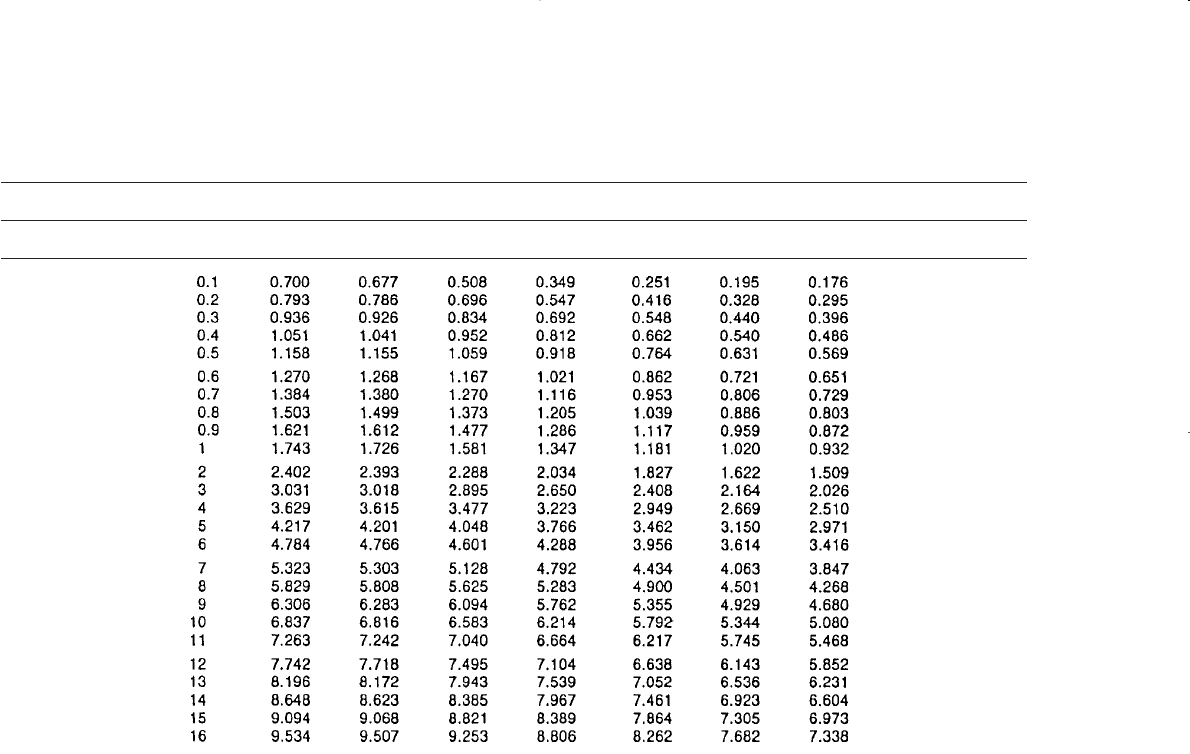
680 Reservoir Engineering Handbook

Table 10-3

Dimensionless Water Influx, W

, for Infinite Aquifer

(Permission to publish by the SPE)

′

0.05 0.1 0.3 0.5 0.7 0.9 1.0

Reservoir Eng Hndbk Ch 10 2001-10-25 14:22 Page 680

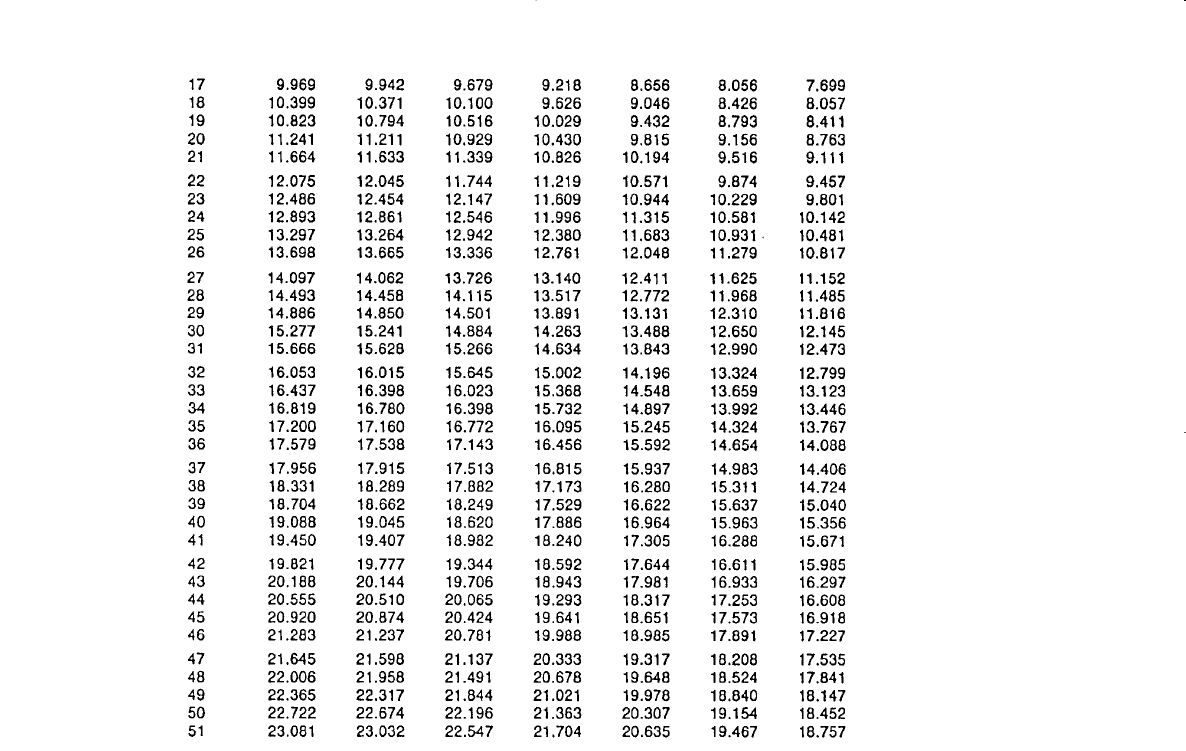
Water Influx 681

(table continued on next page)

Reservoir Eng Hndbk Ch 10 2001-10-25 14:22 Page 681

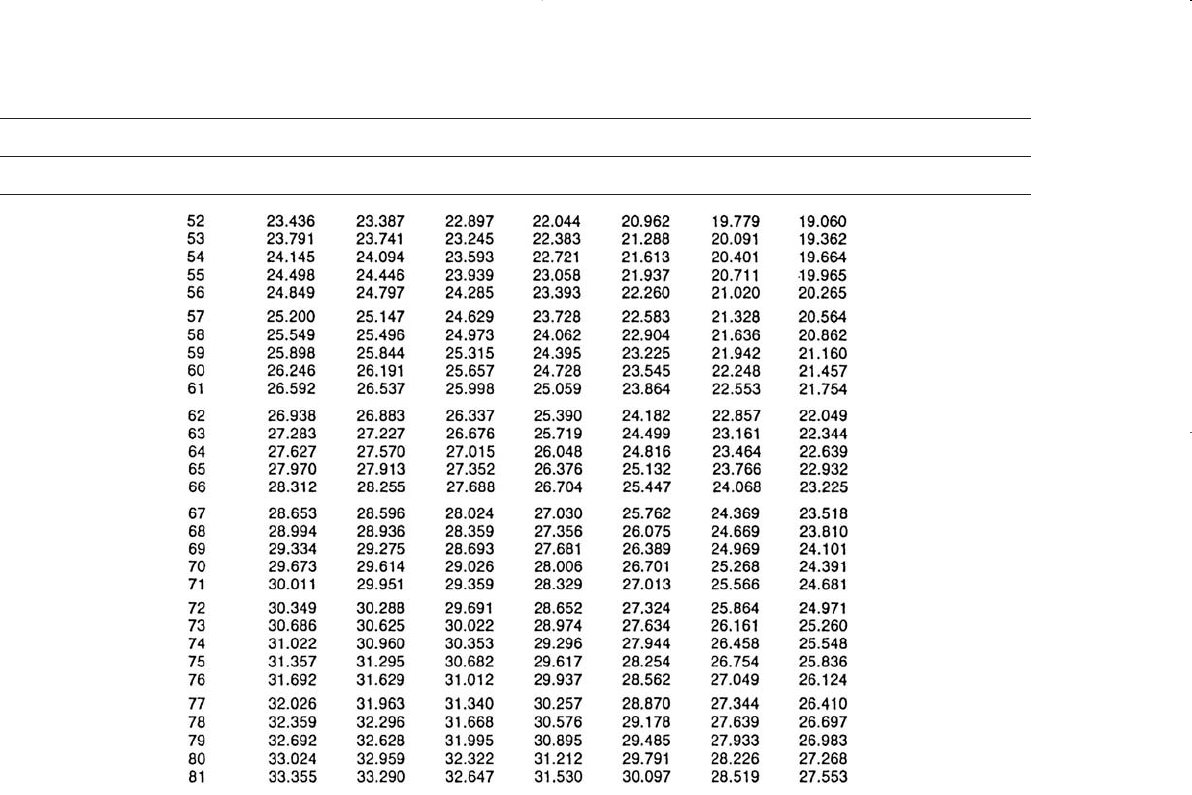
682 Reservoir Engineering Handbook

Table 10-3 (continued)

′

0.05 0.1 0.3 0.5 0.7 0.9 1.0

Reservoir Eng Hndbk Ch 10 2001-10-25 14:23 Page 682

Water Influx 683

(table continued on next page)

Reservoir Eng Hndbk Ch 10 2001-10-25 14:23 Page 683

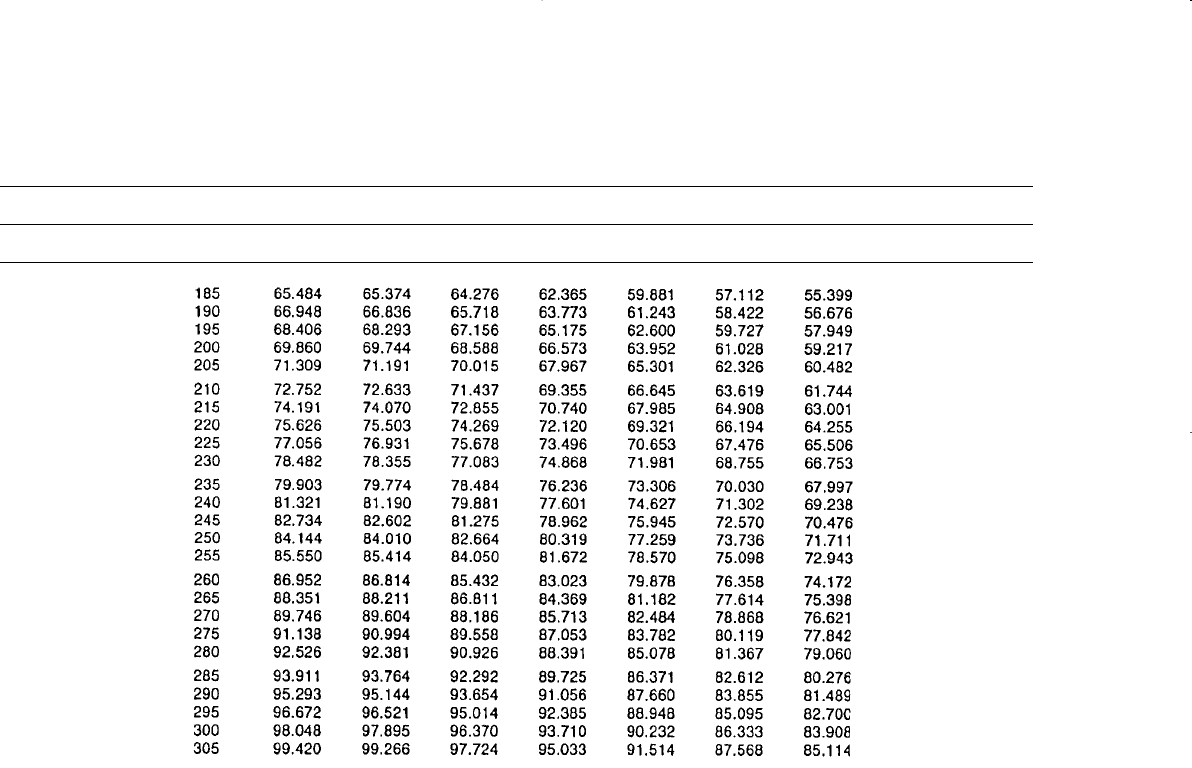
684 Reservoir Engineering Handbook

Table 10-3 (continued)

′

0.05 0.1 0.3 0.5 0.7 0.9 1.0

Reservoir Eng Hndbk Ch 10 2001-10-25 14:23 Page 684

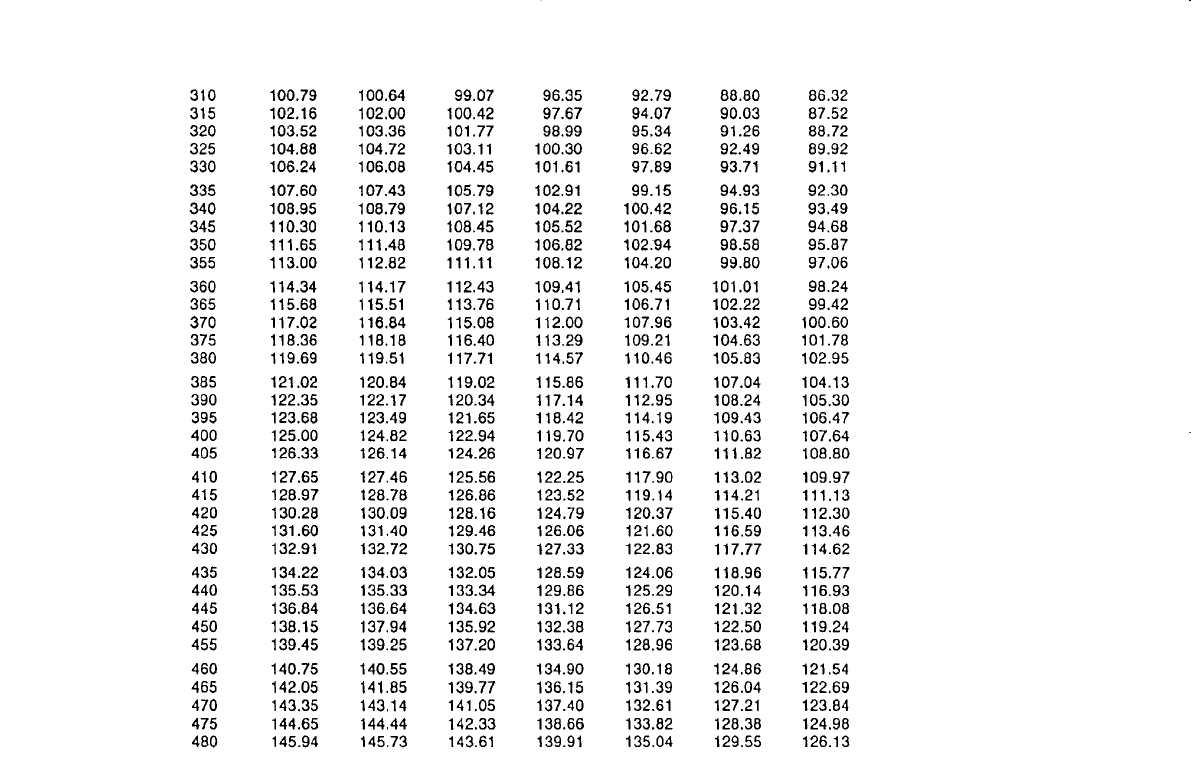
Water Influx 685

(table continued on next page)

Reservoir Eng Hndbk Ch 10 2001-10-25 14:23 Page 685

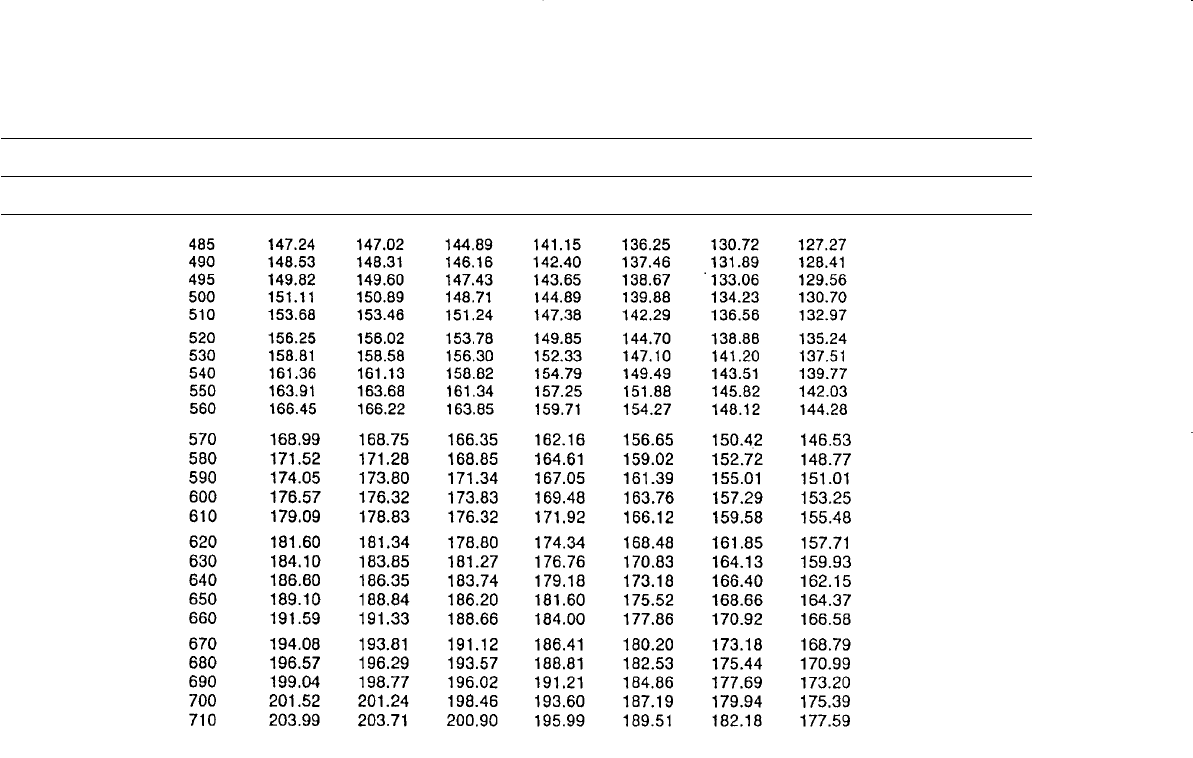
686 Reservoir Engineering Handbook

Table 10-3 (continued)

′

0.05 0.1 0.3 0.5 0.7 0.9 1.0

Reservoir Eng Hndbk Ch 10 2001-10-25 14:23 Page 686

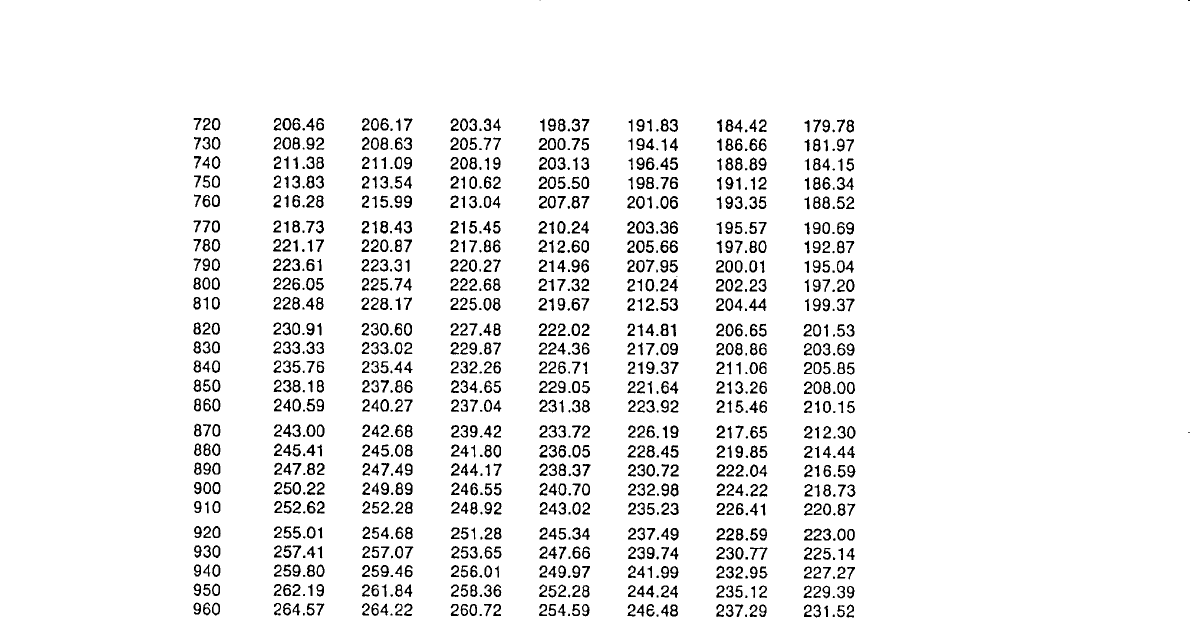
Water Influx 687

(table continued on next page)

Reservoir Eng Hndbk Ch 10 2001-10-25 14:23 Page 687