Tarek Ahmed. Reservoir engineering handbook
Подождите немного. Документ загружается.

Solution
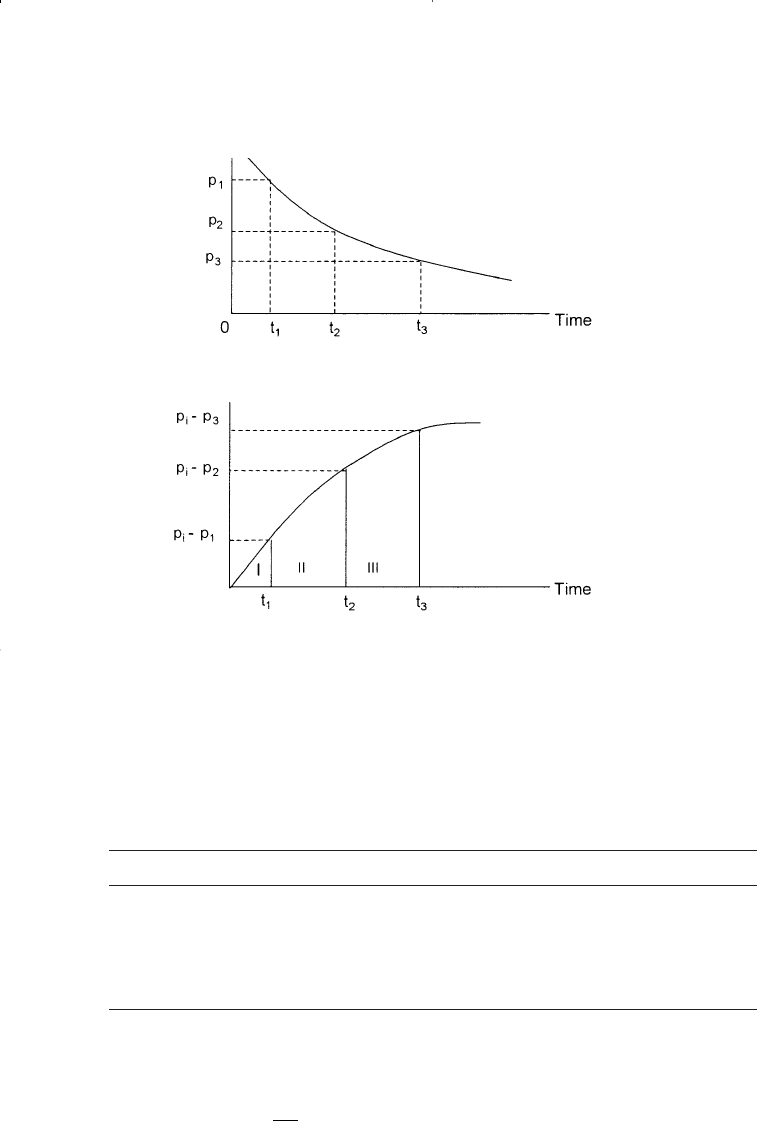
Step 1. Calculate the total pressure drop at each time t.
t, days p p
i
− p
0 3500 0
100 3450 50
200 3410 90
300 3380 120
400 3340 160
Step 2. Calculate the cumulative water influx after 100 days:
W bbl
e
=
−=130
50
2
100 0 325 000(),
648 Reservoir Engineering Handbook
Figure 10-3. Calculating the area under the curve.
Reservoir Eng Hndbk Ch 10 2001-10-25 14:22 Page 648

Step 3. Determine W
e
after 200 days.
Step 4. W
e
after 300 days.
Step 5. Calculate W
e
after 400 days.
Hurst’s Modified Steady-State Model
One of the problems associated with the Schilthuis’ steady-state model
is that as the water is drained from the aquifer, the aquifer drainage
radius r
a
will increase as the time increases. Hurst (1943) proposed that
the “apparent” aquifer radius r
a
would increase with time and, therefore
the dimensionless radius r
a
/r
e
may be replaced with a time dependent
function, as:
r
a
/r
e
= at (10-11)
Substituting Equation 10-11 into Equation 10-7 gives:
The Hurst modified steady-state equation can be written in a more
simplified form as:
e
dW
dt
Cp p
at
w
e
i
==
−()
ln( )
(10 -13)
e
dW
dt
kh p p
at
w
e
i
w
==
−0 00708.()
ln ( )µ
(10 -12)
W
bbl
e
=+++
+
−
=
130 2500 7000 10 500
160 120
2
400 300
4 420 000
,()
,,
W
bbl
e
=
+
+
−
+
+
−
=
130
50
2
100
50 90
2
200 100
120 90
2
300 200 2 600 000
() ( )
(),,
W bbl
e
=
−+
+
−
=130
50
2
100 0
50 90
2
200 100 1 235 000() ( ),,
Water Influx 649
Reservoir Eng Hndbk Ch 10 2001-10-25 14:22 Page 649

and in terms of the cumulative water influx
or
The Hurst modified steady-state equation contains two unknown con-
stants, i.e., a and C, that must be determined from the reservoir-aquifer
pressure and water influx historical data. The procedure of determining
the constants a and C is based on expressing Equation 10-13 as a linear
relationship.
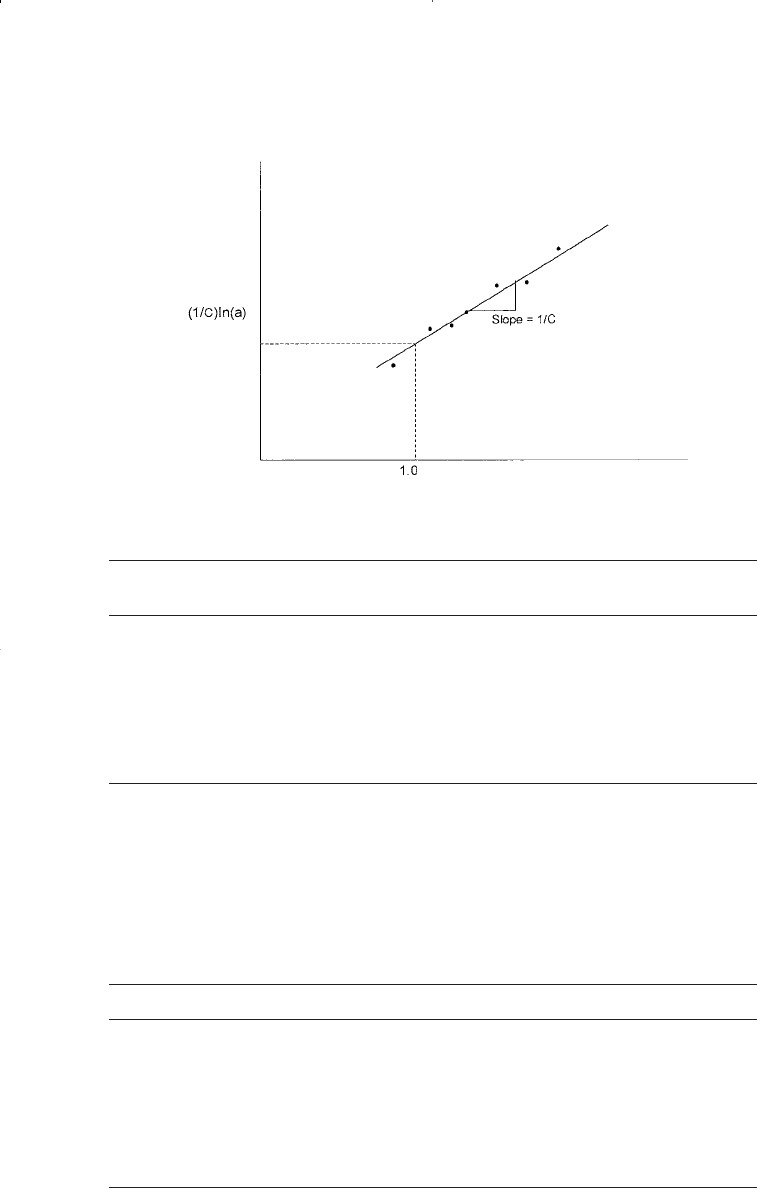
Equation 10-16 indicates that a plot of (p
i
− p)/e
w
versus ln(t) will be a
straight line with a slope of 1/C and intercept of (1/C)ln(a), as shown
schematically in Figure 10-4.
Example 10-5
The following data, as presented by Craft and Hawkins (1959), docu-
ments the reservoir pressure as a function of time for a water-drive
reservoir. Using the reservoir historical data, Craft and Hawkins calcu-
lated the water influx by applying the material balance equation (see
Chapter 11). The rate of water influx was also calculated numerically at
each time period.
pp
eC
at
or
pp
eC
a
C
t
i
w
i
w
−
=
−
=
+
1
11
ln ( )
ln ( ) ln ( ) (10 -16)
WC
p
at
t
e
o
t
=
∑
∆
∆
ln ( )
(10 -15)
WC
pp
at
dt
e
i
o
t
=
−
∫
ln ( )
(10 -14)
650 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 10 2001-10-25 14:22 Page 650
Time Pressure W
e
e
w
p
i
− p
days psi M bbl bbl/day psi
0 3793 0 0 0
182.5 3774 24.8 389 19
365.0 3709 172.0 1279 84
547.5 3643 480.0 2158 150
730.0 3547 978.0 3187 246
912.5 3485 1616.0 3844 308
1095.0 3416 2388.0 4458 377
Assuming that the boundary pressure would drop to 3379 psi after
1186.25 days of production, calculate cumulative water influx at that time.
Solution
Step 1. Construct the following table:
t, days ln(t) p
i
− pe
w
, bbl/day (p
i
− p)/e
w
0— 0 0 —
182.5 5.207 19 389 0.049
365.0 5.900 84 1279 0.066
547.5 6.305 150 2158 0.070
730.0 6.593 246 31.87 0.077
912.5 6.816 308 3844 0.081
1095.0 6.999 377 4458 0.085
Water Influx 651
Figure 10-4. Graphical determination of C and a.
Reservoir Eng Hndbk Ch 10 2001-10-25 14:22 Page 651
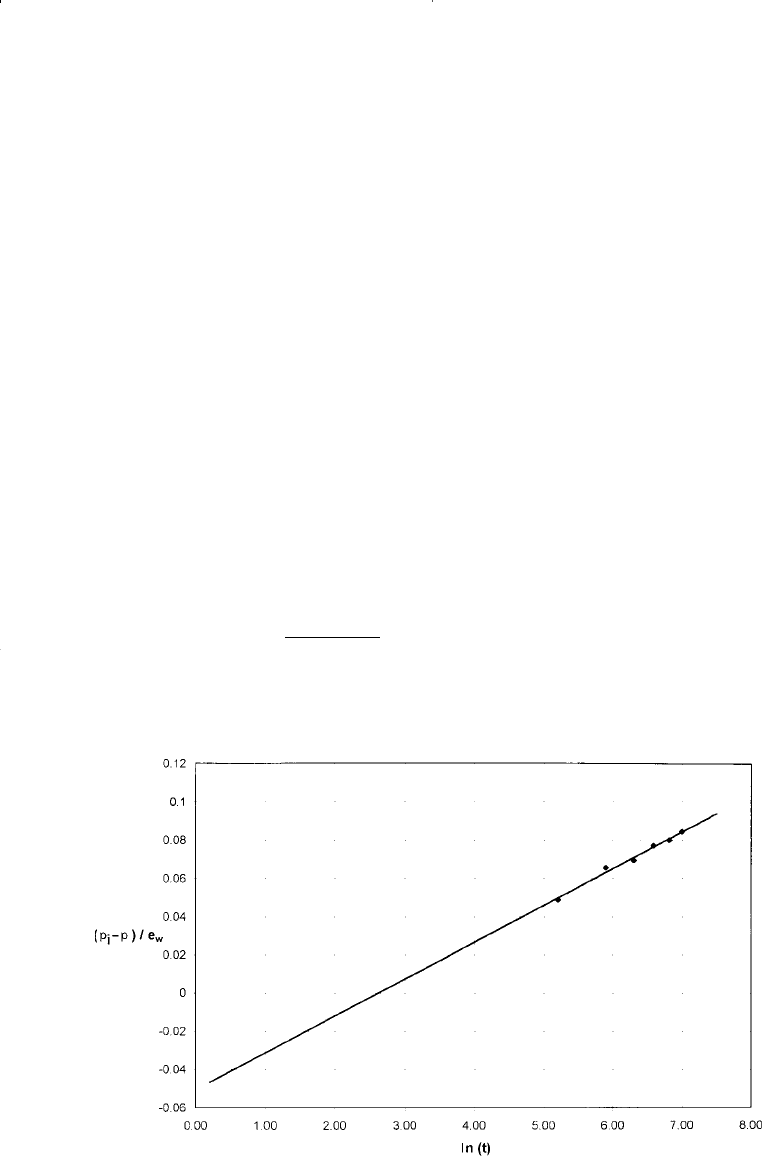
Step 2. Plot the term (p
i
− p)/e
w
versus ln(t) and draw the best straight
line through the points as shown in Figure 10-5, and determine
the slope of the line to give:
slope = 0.020
Step 3. Determine the coefficient C of the Hurst equation from the slope
to give:
C = 1/0.02 = 50
Step 4. Using any point on the straight line, solve for the parameter a by
applying Equation 10-13 to give:
a = 0.064
Step 5. The Hurst equation is represented by:
W
pp
t
dt
e
i
o
t
=
−
∫
50
0 064ln( . )
652 Reservoir Engineering Handbook
Figure 10-5. Determination of C and n for Example 10-5.
Reservoir Eng Hndbk Ch 10 2001-10-25 14:22 Page 652

Step 6. Calculate the cumulative water influx after 1186.25 days from:
The Van Everdingen-Hurst Unsteady-State Model
The mathematical formulations that describe the flow of crude oil sys-
tem into a wellbore are identical in form to those equations that describe
the flow of water from an aquifer into a cylindrical reservoir, as shown
schematically in Figure 10-6.
When an oil well is brought on production at a constant flow rate after
a shut-in period, the pressure behavior is essentially controlled by the
W
pp
t
dt
W
W Mbbl
e
i
e
e
=×+
−
=×+
+
×−
=×+ ×=
∫
−
×
()
−
×
()
2388 10 50
0 064
2388 10 50
2
1186 25 1095
2388 10 420 508 10 2809
3
1095
1186 25
3
3793 3379
0 064 1186 25
3793 3416
0 064 1095
33
ln( . )
(. )
.
.
ln . . ln .
Water Influx 653
Figure 10-6. Water influx into a cylindrical reservoir.
Reservoir Eng Hndbk Ch 10 2001-10-25 14:22 Page 653

transient (unsteady-state) flowing condition. This flowing condition is
defined as the time period during which the boundary has no effect on
the pressure behavior.
The dimensionless form of the diffusivity equation, as presented in
Chapter 6 by Equation 6-90, is basically the general mathematical equa-
tion that is designed to model the transient flow behavior in reservoirs or
aquifers. In a dimensionless form, the diffusivity equation takes the form:
Van Everdingen and Hurst (1949) proposed solutions to the dimen-
sionless diffusivity equation for the following two reservoir-aquifer
boundary conditions:
• Constant terminal rate
• Constant terminal pressure
For the constant-terminal-rate boundary condition, the rate of water
influx is assumed constant for a given period; and the pressure drop at
the reservoir-aquifer boundary is calculated.
For the constant-terminal-pressure boundary condition, a boundary
pressure drop is assumed constant over some finite time period, and the
water influx rate is determined.
In the description of water influx from an aquifer into a reservoir, there
is greater interest in calculating the influx rate rather than the pressure.
This leads to the determination of the water influx as a function of a
given pressure drop at the inner boundary of the reservoir-aquifer system.
Van Everdingen and Hurst solved the diffusivity equation for the
aquifer-reservoir system by applying the Laplace transformation to the
equation. The authors’ solution can be used to determine the water influx
in the following systems:
• Edge-water-drive system (radial system)
• Bottom-water-drive system
• Linear-water-drive system
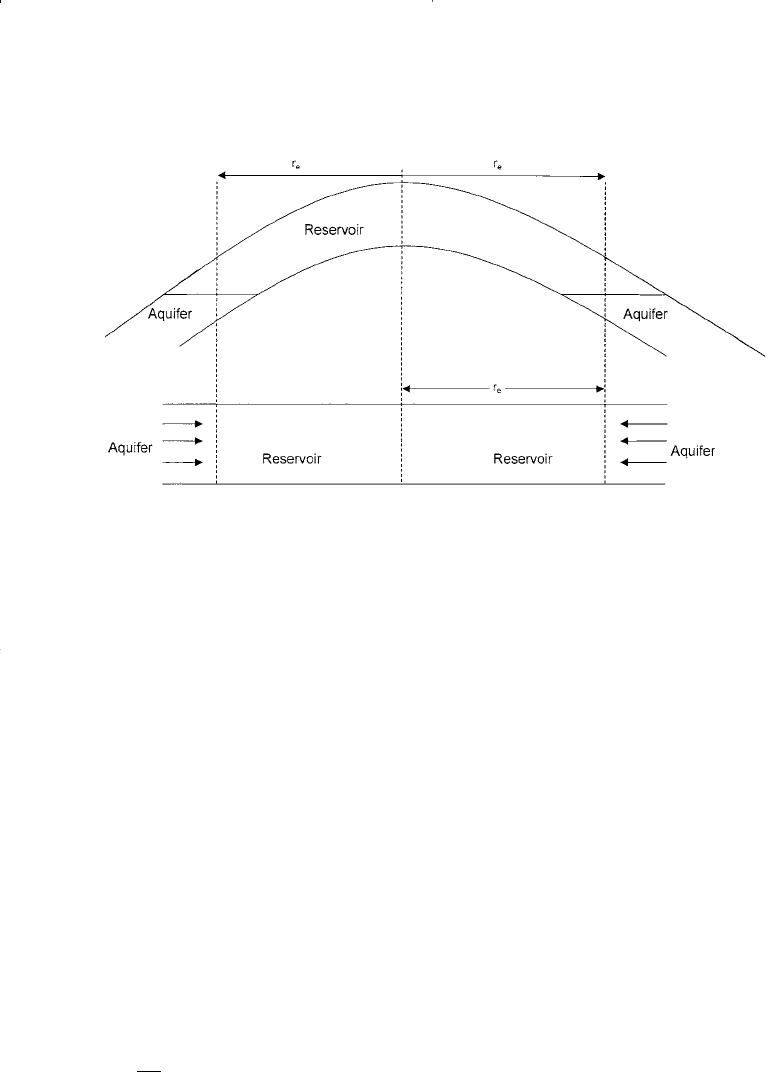
Edge-Water Drive
Figure 10-7 shows an idealized radial flow system that represents an
edge-water-drive reservoir. The inner boundary is defined as the interface
∂
∂
+
∂
∂
=
∂
∂
2
2
1
P
r
r
P
r
P
t
D
D
D
D
D
D
D
654 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 10 2001-10-25 14:22 Page 654
between the reservoir and the aquifer. The flow across this inner bound-
ary is considered horizontal and encroachment occurs across a cylindri-
cal plane encircling the reservoir. With the interface as the inner bound-
ary, it is possible to impose a constant terminal pressure at the inner
boundary and determine the rate of water influx across the interface.
Van Everdingen and Hurst proposed a solution to the dimensionless
diffusivity equation that utilizes the constant terminal pressure condition
in addition to the following initial and outer boundary conditions:
Initial conditions:
p = p
i
for all values of radius r
Outer boundary conditions
• For an infinite aquifer
p = p
i
at r =∞
• For a bounded aquifer
Van Everdingen and Hurst assumed that the aquifer is characterized by:
• Uniform thickness
• Constant permeability
∂
∂
==
p
r
at r r
a
0
Water Influx 655
Figure 10-7. Idealized radial flow model.
Reservoir Eng Hndbk Ch 10 2001-10-25 14:22 Page 655
• Uniform porosity
• Constant rock compressibility
• Constant water compressibility
The authors expressed their mathematical relationship for calculating
the water influx in a form of a dimensionless parameter that is called
dimensionless water influx W
eD
. They also expressed the dimensionless
water influx as a function of the dimensionless time t
D
and dimensionless
radius r
D
, thus they made the solution to the diffusivity equation general-
ized and applicable to any aquifer where the flow of water into the reser-
voir is essentially radial.
The solutions were derived for cases of bounded aquifers and aquifers
of infinite extent. The authors presented their solution in tabulated and
graphical forms as reproduced here in Figures 10-8 through 10-11 and
Tables 10-1 and 10-2.
The two dimensionless parameters t
D
and r
D
are given by:
t
kt
cr
D
wte
=×
−
6 328 10
3
2
.
φµ
(10 -17)
656 Reservoir Engineering Handbook
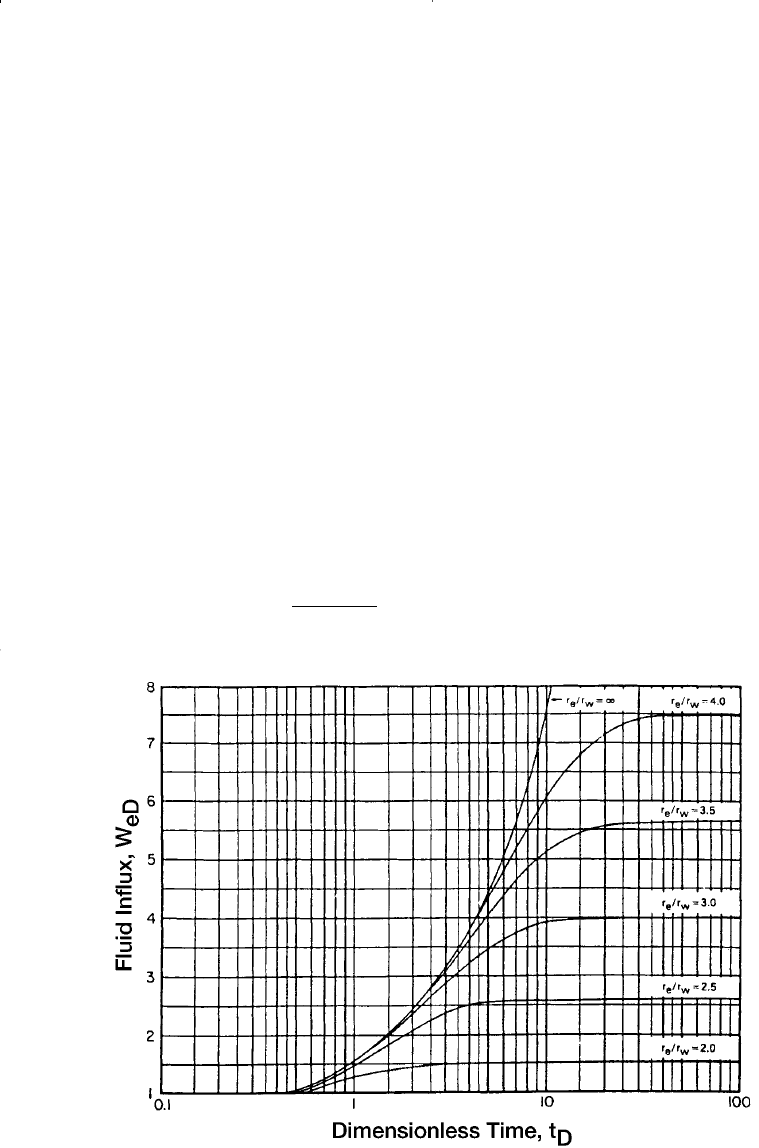
Figure 10-8. Dimensionless water influx W
eD
for several values of r
e
/r
R
, i.e. r
a
/r
e
.
(Van Everdingen and Hurst W
eD
. Permission to publish by the SPE.)
Reservoir Eng Hndbk Ch 10 2001-10-25 14:22 Page 656
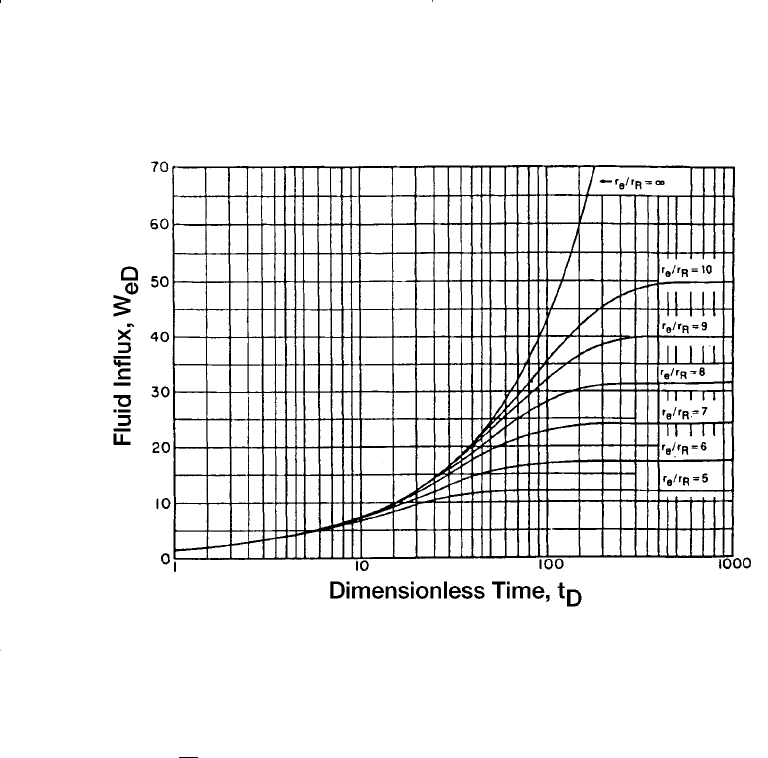
Water Influx 657
Figure 10-9. Dimensionless water influx W
eD
for several values of r
e
/r
R
, i.e. r
a
/r
e
.
(Van Everdingen and Hurst W
eD
. Permission to publish by the SPE.)
c
t
= c
w
+ c
f
(10 - 19)
where t = time, days
k = permeability of the aquifer, md
φ=porosity of the aquifer
µ
w
= viscosity of water in the aquifer, cp
r
a
= radius of the aquifer, ft
r
e
= radius of the reservoir, ft
c
w
= compressibility of the water, psi
−1
c
f
= compressibility of the aquifer formation, psi
−1
c
t
= total compressibility coefficient, psi
−1
The water influx is then given by:
W
e
= B ∆p W
eD
(10-20)
r
r
r
D
a
e
= (10 -18)
Reservoir Eng Hndbk Ch 10 2001-10-25 14:22 Page 657
