Tarek Ahmed. Reservoir engineering handbook
Подождите немного. Документ загружается.

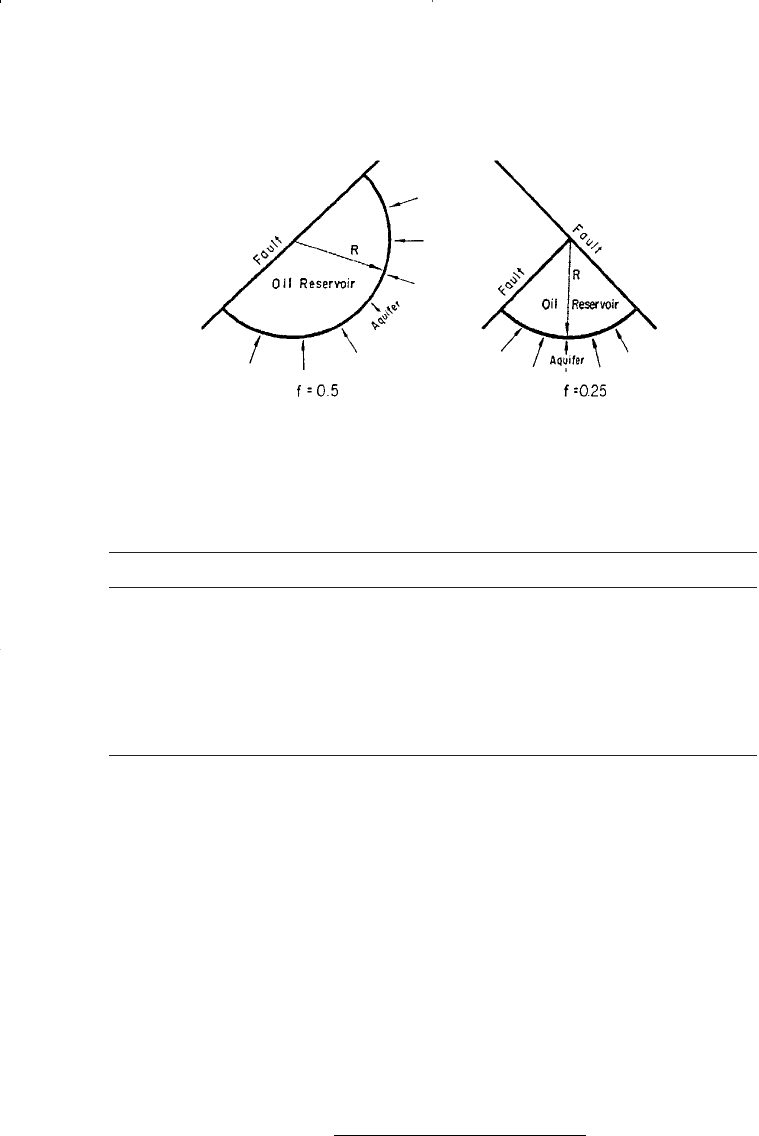
Reservoir Aquifer
radius, ft 2000 ∞
h, ft 20 25
k, md 50 100
φ, % 15 20
µ
w
, cp 0.5 0.8
c
w
, psi
−1
1 × 10
−6
0.7 × 10
−6
c
f
, psi
−1
2 × 10
−6
0.3 × 10
−6
Solution
Step 1. Calculate the total compressibility coefficient c
t
.
c
t
= 0.7 (10
−6
) + 0.3 (10
−3
) = 1 × 10
−6
psi
−1
Step 2. Determine the water influx constant from Equation 10-23.
B = 1.119 (0.2) ( 1 × 10
−6
) (2000)
2
(25) (360/360) = 22.4
Step 3. Calculate the corresponding dimensionless time after 1, 2, and 5
years.
t
D
= 0.9888t
t
t
D
=×
×
−
−
6 328 10
100
0 8 0 2 1 10 2000
3
62
.
(.)(.)( )( )
668 Reservoir Engineering Handbook
(text continued from page 659)
Figure 10-12. Gas cap drive reservoir. (After Cole, F., Reservoir Engineering Man-
ual, Gulf Publishing Company, 1969.)
Reservoir Eng Hndbk Ch 10 2001-10-25 14:22 Page 668

t, days t
D
= 0.9888 t
365 361
730 722
1825 1805
Step 4. Using Table 10-1, determine the dimensionless water influx W
eD
.
t, days t
D
W
eD
365 361 123.5
730 722 221.8
1825 1805 484.6
Step 5. Calculate the cumulative water influx by applying Equation 10-20.
t, days W
eD
W
e
= (20.4) (2500 − 2490) W
eD
365 123.5 25,200 bbl
730 221.8 45,200 bbl
1825 484.6 98,800 bbl
Example 10-6 shows that, for a given pressure drop, doubling the time
interval will not double the water influx. This example also illustrates
how to calculate water influx as a result of a single pressure drop. As
there will usually be many of these pressure drops occurring throughout
the prediction period, it is necessary to analyze the procedure to be used
where these multiple pressure drops are present.
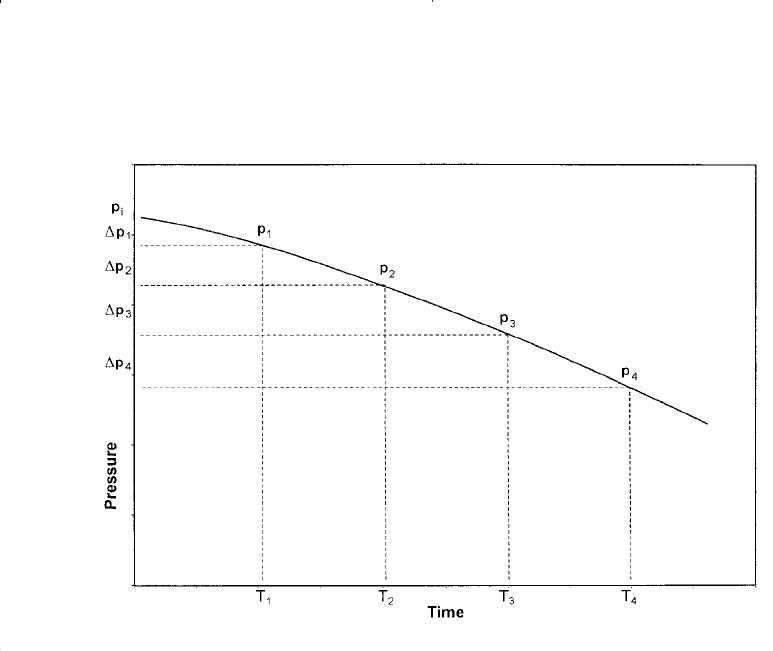
Consider Figure 10-13, which illustrates the decline in the boundary
pressure as a function of time for a radial reservoir-aquifer system. If the
boundary pressure in the reservoir shown in Figure 10-13 is suddenly
reduced at time t, from p
i
to p
1
, a pressure drop of (p
i
− p
1
) will be
imposed across the aquifer. Water will continue to expand and the new
reduced pressure will continue to move outward into the aquifer. Given a
sufficient length of time the pressure at the outer edge of the aquifer will
finally be reduced to p
1
.
If some time after the boundary pressure has been reduced to p
1
, a sec-
ond pressure p
2
is suddenly imposed at the boundary, and a new pressure
wave will begin moving outward into the aquifer. This new pressure
wave will also cause water expansion and therefore encroachment into
the reservoir. This new pressure drop, however, will not be p
i
− p
2
, but
will be p
1
− p
2
. This second pressure wave will be moving behind the
Water Influx 669
Reservoir Eng Hndbk Ch 10 2001-10-25 14:22 Page 669
first pressure wave. Just ahead of the second pressure wave will be the
pressure at the end of the first pressure drop, p
1
.
Since these pressure waves are assumed to occur at different times, they
are entirely independent of each other. Thus, water expansion will contin-
ue to take place as a result of the first pressure drop, even though addition-
al water influx is also taking place as a result of one or more later pressure
drops. This is essentially an application of the principle of superposition.
In order to determine the total water influx into a reservoir at any given
time, it is necessary to determine the water influx as a result of each suc-
cessive pressure drop that has been imposed on the reservoir and aquifer.
In calculating cumulative water influx into a reservoir at successive
intervals, it is necessary to calculate the total water influx from the
beginning. This is required because of the different times during which
the various pressure drops have been effective.
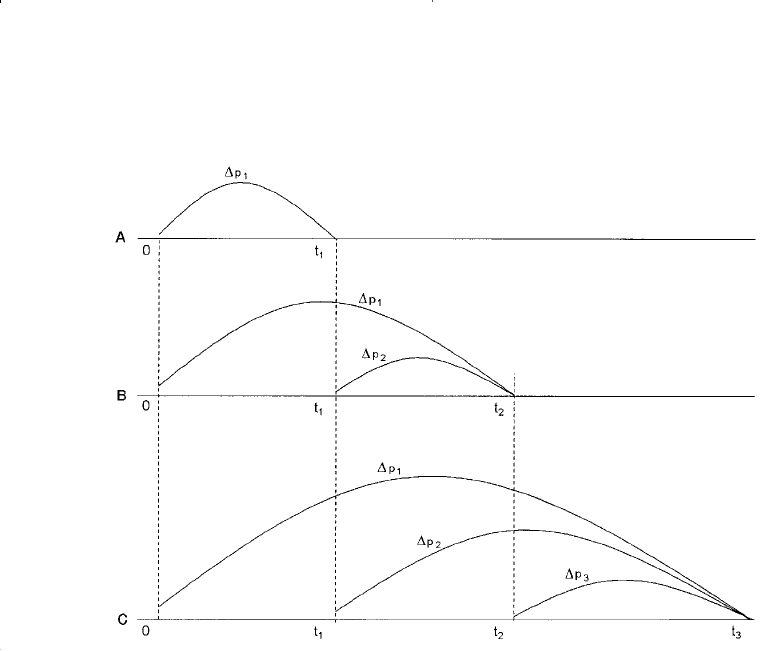
The van Everdingen-Hurst computational steps for determining the
water influx are summarized below in conjunction with Figure 10-14:
Step 1. Assume that the boundary pressure has declined from its initial
value of p
i
to p
1
after t
1
days. To determine the cumulative water
670 Reservoir Engineering Handbook
Figure 10-13. Boundary pressure versus time.
Reservoir Eng Hndbk Ch 10 2001-10-25 14:22 Page 670
influx in response to this first pressure drop, ∆p
1
= p
i
− p
1
can be
simply calculated from Equation 10-20, or:
W
e
= B ∆p
1
(W
eD
)
t
1
Where W
e
is the cumulative water influx due to the first pres-
sure drop ∆p
1
. The dimensionless water influx (W
eD
)
t
1
is evaluat-
ed by calculating the dimensionless time at t
1
days. This simple
calculation step is shown in section A of Figure 10-14.
Step 2. Let the boundary pressure decline again to p
2
after t
2
days with a
pressure drop of ∆p
2
= p
1
− p
2
. The cumulative (total) water
influx after t
2
days will result from the first pressure drop ∆p
1
and
the second pressure drop ∆p
2
, or:
W
e
= water influx due to ∆p
1
+ water influx due to ∆p
2
W
e
= (W
e
)
∆p
1
+ (W
e
)
∆p
2
Water Influx 671
Figure 10-14. Illustration of the superposition concept.
Reservoir Eng Hndbk Ch 10 2001-10-25 14:22 Page 671

where
(W
e
)
∆p
1
= B ∆p
1
(W
eD
)
t
2
(W
e
)
∆p
2
= B ∆p
2
(W
eD
)
t
2
− t
1
The above relationships indicate that the effect of the first pres-
sure drop ∆p
1
will continue for the entire time t
2
, while the effect
of the second pressure drop will continue only for (t
2
− t
1
) days as
shown in section B of Figure 10-14.
Step 3. A third pressure drop of ∆p
3
= p
2
− p
3
would cause an additional
water influx as illustrated in section C of Figure 10-14. The cumu-
lative (total) cumulative water influx can then be calculated from:
W
e
= (W
e
)
∆p
1
+ (W
e
)
∆p
2
+ (W
e
)
∆p
3
where
(W
e
)
∆p
1
= B ∆p
1
(W
eD
)
t
3
(W
e
)
∆p
2
= B ∆p
2
(W
eD
)
t
3
− t
1
(W
e
)
∆p
3
= B ∆p
3
(W
eD
)
t
3
− t
2
The van Everdingen-Hurst water influx relationship can then be
expressed in a more generalized form as:
W
e
= B Σ ∆p W
eD
(10-24)
The authors also suggested that instead of using the entire pressure drop
for the first period, a better approximation is to consider that one-half of
the pressure drop,
1
⁄2 (p
i
− p
1
), is effective during the entire first period. For
the second period, the effective pressure drop then is one-half of the pres-
sure drop during the first period,
1
⁄2 (p
i
− p
2
), which simplifies to:
1
⁄2 (p
i
− p
1
) +
1
⁄2 (p
1
− p
2
) =
1
⁄2 (p
i
− p
2
)
Similarly, the effective pressure drop for use in the calculations for the
third period would be one-half of the pressure drop during the second
period,
1
⁄2 (p
1
− p
2
), plus one-half of the pressure drop during the third
period,
1
⁄2 (p
2
− p
3
), which simplifies to
1
⁄2 (p
1
− p
3
). The time intervals
must all be equal in order to preserve the accuracy of these modifications.
672 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 10 2001-10-25 14:22 Page 672

Example 10-7
Using the data given in Example 10-6, calculate the cumulative water
influx at the end of 6, 12, 18, and 24 months. The predicted boundary
pressure at the end of each specified time period is given below:
Time, months Boundary pressure, psi
0 2500
6 2490
12 2472
18 2444
24 2408
Solution
Water influx at the end of 6 months
Step 1. Determine water influx constant B:
B = 22.4 bbl/psi
Step 2. Calculate the dimensionless time t
D
at 182.5 days.
t
D
= 0.9888t
= 0.9888 (182.5) = 180.5
Step 3. Calculate the first pressure drop ∆p
1
. This pressure is taken as
1
⁄
2
of the actual pressure drop, or:
Step 4. Determine the dimension water influx W
eD
from Table 10-1 at
t
D
= 180.5 to give:
W
eD
= 69.46
∆p psi
1
2500 2490
2
5=
−
=
∆p
pp
i
1
1
2
=
−
Water Influx 673
Reservoir Eng Hndbk Ch 10 2001-10-25 14:22 Page 673

Step 5. Calculate the cumulative water influx at the end of 182.5 days
due to the first pressure drop of 5 psi by using the van Everdin-
gen-Hurst equation, or:
W
e
= (20.4) (5 ) (69.46) = 7080 bbl
Cumulative water influx after 12 months
Step 1. After an additional six months, the pressure has declined from
2490 psi to 2472 psi. This second pressure ∆p
2
is taken as one-
half the actual pressure drop during the first period, plus one-half
the actual pressure drop during the second period, or:
Step 2. The cumulative (total) water influx at the end of 12 months would
result from the first pressure drop ∆p
1
and the second pressure
drop ∆p
2
.
The first pressure drop ∆p
1
has been effective for one year, but
the second pressure drop, ∆p
2
, has been effective only 6 months,
as shown in Figure 10-15.
Separate calculations must be made for the two pressure drops
because of this time difference and the results added in order to
determine the total water influx, i.e.:
W
e
= (W
e
)
∆p
1
+ (W
e
)
∆p
2
∆p
pp
psi
i
2
2
2
2500 2472
2
14
=
−
=
−
=
674 Reservoir Engineering Handbook
Figure 10-15. Duration of the pressure drop in Example 10-7.
Reservoir Eng Hndbk Ch 10 2001-10-25 14:22 Page 674

Step 3. Calculate the dimensionless time at 365 days as:
t
D
= 0.9888t
= 0.9888 (365) = 361
Step 4. Determine the dimensionless water influx at t
D
= 361 from Table
10-1 to give:
W
eD
= 123.5
Step 5. Calculate the water influx due to the first and second pressure
drop, i.e., (W
e
)
∆p
1
and (W
e
)
∆p
2
, or:
(W
e
)
∆p
1
= (20.4)(5)(123.5) = 12,597 bbl
(W
e
)
∆p
2
= (20.4)(14)(69.46) = 19,838
Step 6. Calculate total (cumulative) water influx after one year.
W
e
= 12,597 + 19,938 = 32,435 bbl
Water influx after 18 months
Step 1. Calculate the third pressure drop ∆p
3
which is taken as
1
⁄2 of the
actual pressure drop during the second period plus
1
⁄2
of the actual
pressure drop during the third period, or:
Step 2. Calculate the dimensionless time after 6 months.
t
D
= 0.9888 t
= 0.9888 (547.5) = 541.5
Step 3. Determine the dimensionless water influx at:
t
D
= 541.5 from Table 10-1
W
eD
= 173.7
∆
∆
p
pp
p psi
3
13
3
2
2490 2444
2
23
=
−
=
−
=
Water Influx 675
Reservoir Eng Hndbk Ch 10 2001-10-25 14:22 Page 675

Step 4. The first pressure drop will have been effective the entire 18
months, the second pressure drop will have been effective for 12
months, and the last pressure drop will have been effective only 6
months, as shown in Figure 10-16. Therefore, the cumulative
water influx is calculated below:
Time, days t
D
∆pW
eD
B∆p W
eD
547.5 541.5 5 173.7 17,714
365 361 14 123.5 35,272
182.5 180.5 23 69.40 32,291
W
e
= 85,277 bbl
Water influx after two years
The first pressure drop has now been effective for the entire two
years, the second pressure drop has been effective for 18 months, the
third pressure drop has been effective for 12 months, and the fourth
pressure drop has been effective only 6 months. Summary of the calcu-
lations is given below:
Time, days t
D
∆pW
eD
B∆p W
eD
730 722 5 221.8 22,624
547.5 541.5 14 173.7 49,609
365 631 23 123.5 57,946
182.5 180.5 32 69.40 45,343
W
e
= 175,522 bbl
Edwardson and coworkers (1962) developed three sets of simple poly-
nomial expressions for calculating the dimensionless water influx W
eD
for
676 Reservoir Engineering Handbook
Figure 10-16. Pressure drop data for Example 10-7.
Reservoir Eng Hndbk Ch 10 2001-10-25 14:22 Page 676
infinite-acting aquifers. The proposed three expressions essentially
approximate the W
eD
values in three different dimensionless time regions.
• For t
D
< 0.01
• For 0.01 < t
D
< 200
• For t
D
> 200
Bottom-Water Drive
The van Everdingen-Hurst solution to the radial diffusivity equation is
considered the most rigorous aquifer influx model to date. The proposed
solution technique, however, is not adequate to describe the vertical
water encroachment in bottom-water-drive system. Coats (1962) present-
ed a mathematical model that takes into account the vertical flow effects
from bottom-water aquifers. He correctly noted that in many cases reser-
voirs are situated on top of an aquifer with a continuous horizontal inter-
face between the reservoir fluid and the aquifer water and with a signifi-
cant aquifer thickness. He stated that in such situations significant
bottom-water drive would occur. Coats modified the diffusivity equation
to account for the vertical flow by including an additional term in the
equation, to give:
where F
k
is the ratio of vertical to horizontal permeability, or:
F
k
= k
v
/k
h
(10 -29)
∂
∂
+
∂
∂
+
∂
∂
=
∂
∂
2
2
2
2
1p
r
r
p
r
F
p
z
c
k
p
t
k
µφ
(10 - 28)
W
t
t
eD
D
D
=
−+4 29881 2 02566..
ln ( )
(10 - 27)
W
1.2838 t 1.19328t 0.269872(t ) 0.00855294(t )
1 0.616599 t 0.0413008 t
(10 - 26)
eD
DD D
3/2
D
2
DD
=
++ +
++
W
t
eD
D
=
2
05
π
.
(10 - 25)
Water Influx 677
Reservoir Eng Hndbk Ch 10 2001-10-25 14:22 Page 677
