Tarek Ahmed. Reservoir engineering handbook
Подождите немного. Документ загружается.

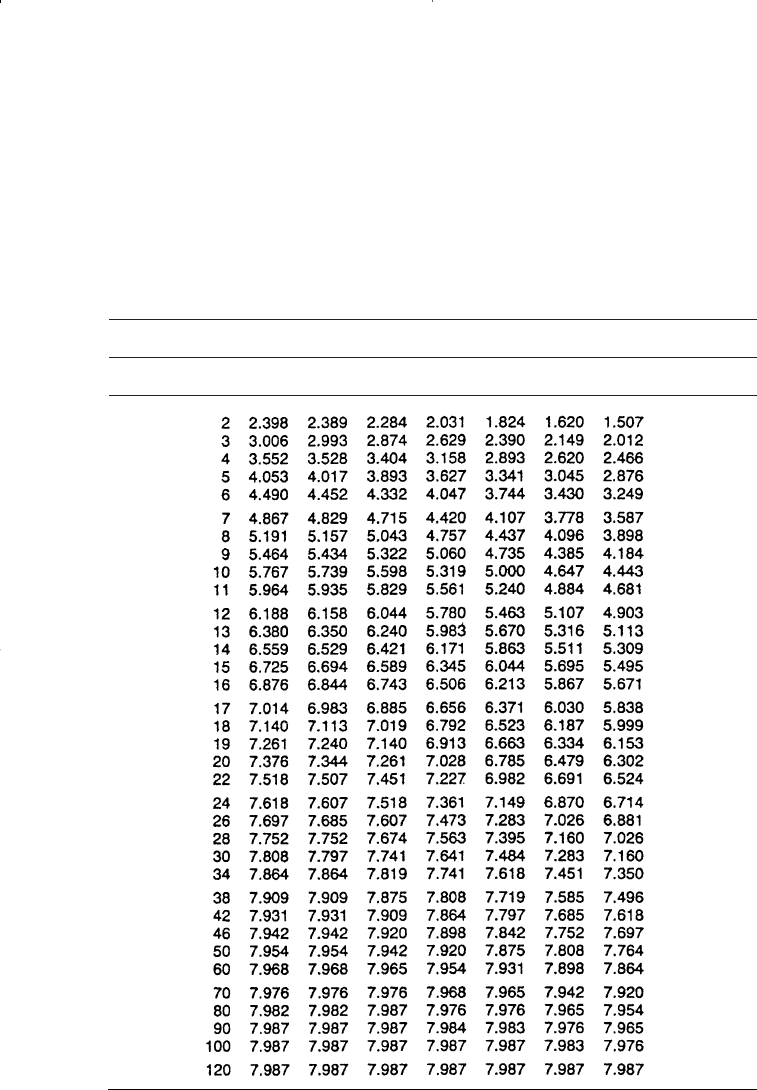
698 Reservoir Engineering Handbook
Table 10-4
Dimensionless Water Influx, W
eD
, for r′
D
= 4
(Permission to publish by the SPE)
z
D
′
t
D
0.05 0.1 0.3 0.5 0.7 0.9 1.0
Reservoir Eng Hndbk Ch 10 2001-10-25 14:23 Page 698

Water Influx 699
Table 10-5
Dimensionless Water Influx, W
eD
, for r′
D
= 6
(Permission to publish by the SPE)
z
D
′
t
D
0.05 0.1 0.3 0.5 0.7 0.9 1.0
Reservoir Eng Hndbk Ch 10 2001-10-25 14:23 Page 699
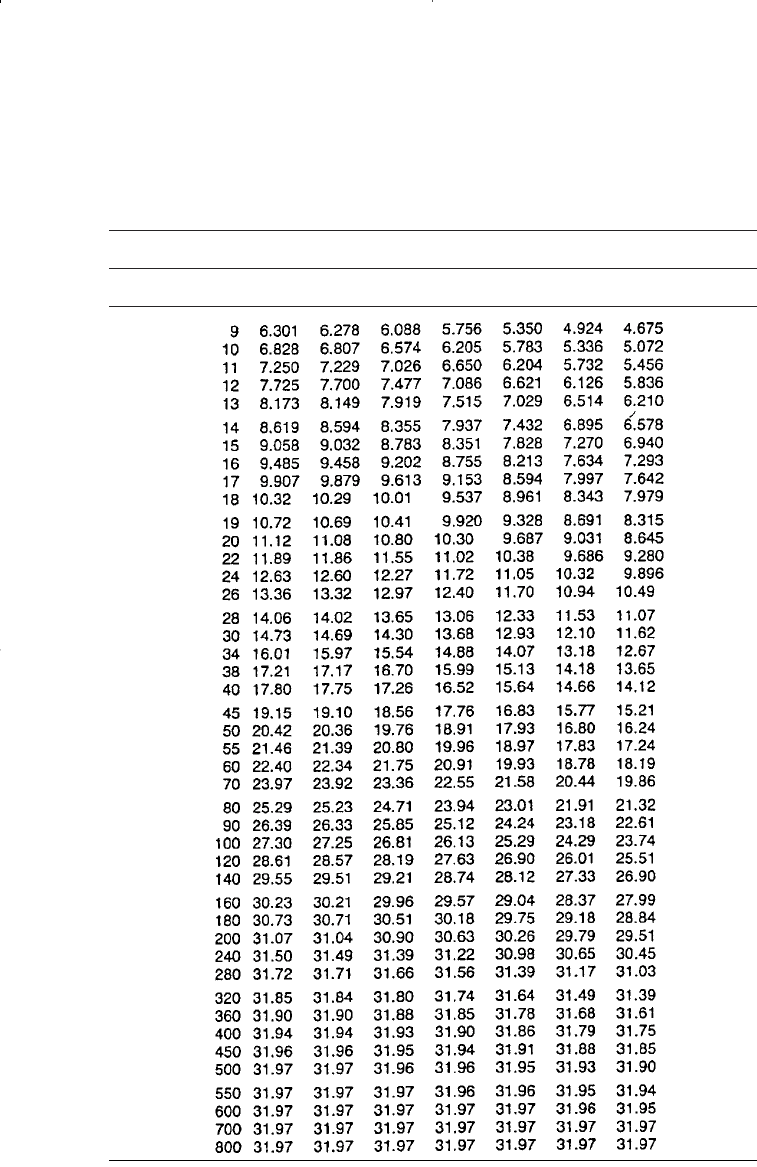
700 Reservoir Engineering Handbook
Table 10-6
Dimensionless Water Influx, W
eD
, for r′
D
= 8
(Permission to publish by the SPE)
z
D
′
t
D
0.05 0.1 0.3 0.5 0.7 0.9 1.0
Reservoir Eng Hndbk Ch 10 2001-10-25 14:23 Page 700
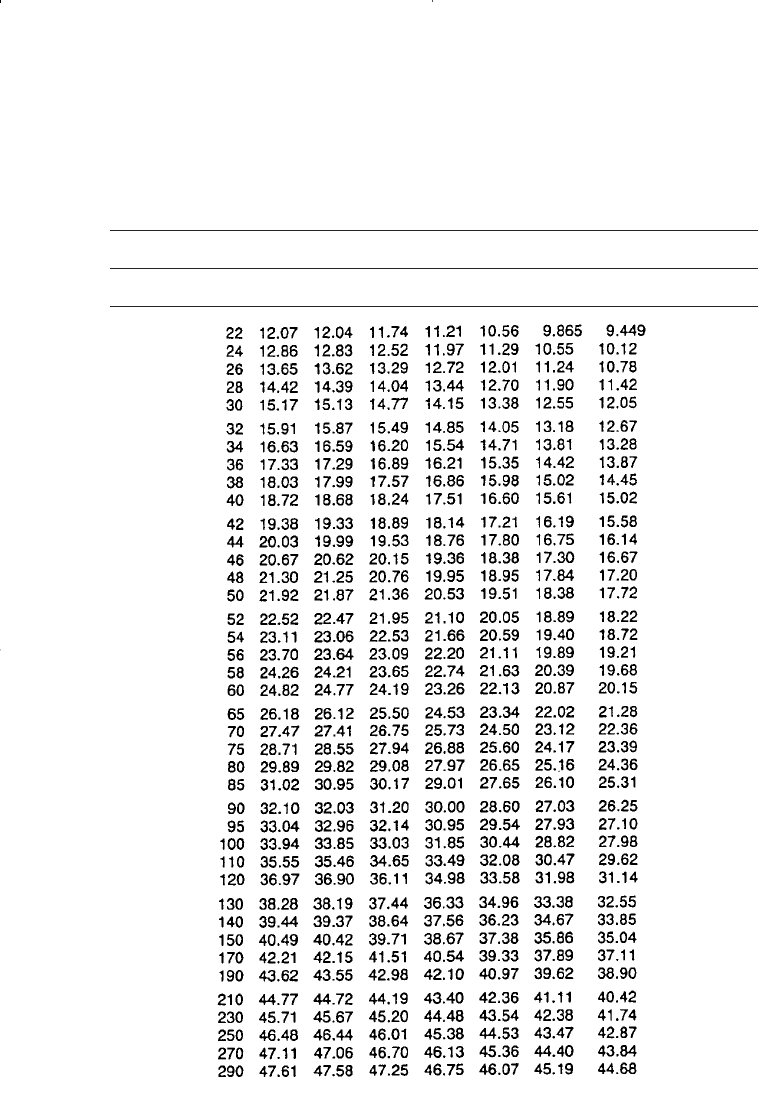
Water Influx 701
Table 10-7
Dimensionless Water Influx W
eD
for r
D
= 10
(Permission to publish by the SPE)
z
D
′
t
D
0.05 0.1 0.3 0.5 0.7 0.9 1.0
(table continued on next page)
Reservoir Eng Hndbk Ch 10 2001-10-25 14:23 Page 701

702 Reservoir Engineering Handbook
Step 4. Calculate the dimensionless time t
D
.
t
D
= 0.2503 t
Step 5. Calculate the water influx.
t ∆p Bottom-Water Model Edge-Water Model
Days t
D
psi W
eD
W
e
, Mbbl W
eD
W
e
, Mbbl
00 0 — — — —
30 7.5 22 5.038 79 6.029 95
60 15.0 41.5 8.389 282 9.949 336
90 22.5 39.5 11.414 572 13.459 678
120 30.0 36.5 14.994 933 16.472 1,103
150 37.5 33.0 16.994 1,353 19.876 1,594
180 45.0 26.5 19.641 1,810 22.897 2,126
210 52.5 19.0 22.214 2,284 25.827 2,676
240 60.0 18.0 24.728 2,782 28.691 3,250
tt
D
=×
×
−
−
6 328 10
50
0 1 0 395 8 10 2000
3
62
.
(.)(. )( )( )
(text continued from page 679)
Table 10-7 (continued)
z
D
′
t
D
0.05 0.1 0.3 0.5 0.7 0.9 1.0
Reservoir Eng Hndbk Ch 10 2001-10-25 14:23 Page 702

Water Influx 703
The Carter-Tracy Water Influx Model
Van Everdingen-Hurst methodology provides the exact solution to the
radial diffusivity equation and therefore is considered the correct tech-
nique for calculating water influx. However, because superposition of
solutions is required, their method involves tedious calculations. To
reduce the complexity of water influx calculations, Carter and Tracy
(1960) proposed a calculation technique that does not require superposi-
tion and allows direct calculation of water influx.
The primary difference between the Carter-Tracy technique and the
van Everdingen-Hurst technique is that the Carter-Tracy technique
assumes constant water influx rates over each finite time interval. Using
the Carter-Tracy technique, the cumulative water influx at any time, t
n
,
can be calculated directly from the previous value obtained at t
n − 1
, or:
where B = the van Everdingen-Hurst water influx constant as defined
by Equation 10-23
t
D
= the dimensionless time as defined by Equation 10-17
n = refers to the current time step
n − 1 = refers to the previous time step
∆p
n
= total pressure drop, p
i
− p
n
, psi
p
D
= dimensionless pressure
p′
D
= dimensionless pressure derivative
Values of the dimensionless pressure p
D
as a function of t
D
and r
D
are
tabulated in Chapter 6, Table 6-2. In addition to the curve-fit equations
given in Chapter 6 (Equations 6-91 through 6-96), Edwardson and co-
authors (1962) developed the following approximation of p
D
for an infi-
nite-acting aquifer.
p
tt t
ttt
D
DD D
DDD
=
++
+++
370 529 137 582 5 69549
328 834 265 488 45 2157
15
15
...()
.. .()
.
.
(10 - 34)
() () [()()]
()()
() () ()
WW t t
Bp W p
ptp
en en Dn Dn
nenDn
Dn Dn Dn
=+−
−
′
−
′
−−
−
−
11
1
1
∆
(10 - 33)
Reservoir Eng Hndbk Ch 10 2001-10-25 14:23 Page 703

704 Reservoir Engineering Handbook
The dimensionless pressure derivative can then be approximated by
where E = 716.441 + 46.7984 (t
D
)
0.5
+ 270.038 t
D
+ 71.0098 (t
D
)
1.5
F = 1296.86 (t
D
)
0.5
+1204.73 t
D
+ 618.618 (t
d
)
1.5
+ 538.072 (t
D
)
2
+ 142.41 (t
D
)
2.5
The following approximation could also be used between t
D
> 100:
p
D
= 0.5 [Ln (t
D
) + 0.80907]
with the derivative as given by:
= 1/(2t
D
)
It should be noted that the Carter-Tracy method is not an exact solution
to the diffusivity equation and should be considered an approximation.
Example 10-9
Rework Example 10-7 by using the Carter-Tracy method.
Solution
Example 10-7 shows the following preliminary results:
• Water influx constant B = 20.4 bbl/psi
•t
D
= 0.9888 t
Step 1. For each time step n, calculate the total pressure drop ∆p
n
= p
i
− p
n
and the corresponding t
D
N t, days p
n
∆p
n
t
D
0 0 2500 0 0
1 182.5 2490 10 180.5
2 365.0 2472 28 361.0
3 547.5 2444 56 541.5
4 730.0 2408 92 722.0
Step 2. Since values of t
D
are greater than 100, use Equation 6-92 to cal-
culate p
D
and its derivative p′
D
, i.e.,
p
D
= 0.5 [Ln (t
D
) + 0.80907]
p′
D
= 1/(2 t
D
)
′
p
D
′
=p
E
F
(10 - 35)
D
Reservoir Eng Hndbk Ch 10 2001-10-25 14:23 Page 704

Water Influx 705
Nt t
D
p
D
p
D
′
00 0 — —
1 182.5 180.5 3.002 2.770 × 10
−3
2 365 361.0 3.349 1.385 × 10
−3
3 547.5 541.5 3.552 0.923 × 10
−3
4 730.0 722.0 3.696 0.693 × 10
−3
Step 3. Calculate cumulative water influx by applying Equation 10-33.
• W
e
after 182.5 days:
W
e
= 12,266 bbl
• W
e
after 365 days:
= 42,546 bbl
• W
e
after 547.5 days:
W
e
= 104,406
• W
e
after 720 days:
W
e
= 202,477 bbl
W
e
=+−
−×
−×
−
−
104 406 722 541 5
20 4 92 104 406 0 693 10
3 696 541 5 0 693 10
3
3
,[ .]
(.)()( , )(. )
.(.)(. )
W
e
=+−
−×
−×
−
−
42 546 541 5 361
20 4 56 42 546 0 923 10
3 552 361 0 923 10
3
3
,[. ]
(.)()(, )(. )
.()(. )
W
e
=+−
−×
−×
−
−
12 266 361 180 5
20 4 28 12 266 1 385 10
3 349 180 5 1 385 10
3
3
,[ .]
(.)()(, )(. )
.(.)(. )
W
e
=+ −
−×
−×
−
−
0 180 5 0
20 4 10 0 2 77 10
3 002 0 2 77 10
3
3
[. ]
( . )( ) ( )( . )
.()(. )
Reservoir Eng Hndbk Ch 10 2001-10-25 14:23 Page 705

706 Reservoir Engineering Handbook
The following table compares results of the Carter-Tracy water influx
calculations with those of the van Everdingen-Hurst method.
Carter-Tracy Van Everdingen-Hurst
Time, month W
e
, bbl W
e
, bbl
00 0
6 12,266 7,080
12 42,546 32,435
18 104,400 85,277
24 202,477 175,522
The above comparison indicates that the Carter-Tracy method consid-
erably overestimates the water influx. This is due, however, to the fact
that a large time-step of 6 months was used in the Carter-Tracy method to
determine the water influx. Accuracy of the Carter-Tracy method can be
increased substantially by restricting the time step used in performing the
water influx calculations to less than 30 days, i.e. ∆t = 30 days. Recalcu-
lating the water influx on monthly basis produces an excellent match
with the van Everdingen-Hurst method as shown below.
Carter- van Everdingen-
Tracy Hurst
time time p ∆pW
e
W
e
months days psi psi t
D
p
D
p´
D
bbl bbl
0 0 2500.0 0.00 0 0.00 0 0.0 0
1 30 2498.9 1.06 30.0892 2.11 0.01661 308.8
2 61 2497.7 2.31 60.1784 2.45 0.00831 918.3
3 91 2496.2 3.81 90.2676 2.66 0.00554 1860.3
4 122 2494.4 5.56 120.357 2.80 0.00415 3171.7
5 152 2492.4 7.55 150.446 2.91 0.00332 4891.2
6 183 2490.2 9.79 180.535 3.00 0.00277 7057.3 7088.9
7 213 2487.7 12.27 210.624 3.08 0.00237 9709.0
8 243 2485.0 15.00 240.713 3.15 0.00208 12884.7
9 274 2482.0 17.98 270.802 3.21 0.00185 16622.8
10 304 2478.8 21.20 300.891 3.26 0.00166 20961.5
11 335 2475.3 24.67 330.981 3.31 0.00151 25938.5
12 365 2471.6 28.38 361.070 3.35 0.00139 31591.5 32438.0
13 396 2467.7 32.34 391.159 3.39 0.00128 37957.8
14 426 2463.5 36.55 421.248 3.43 0.00119 45074.5
15 456 2459.0 41.00 451.337 3.46 0.00111 52978.6
16 487 2454.3 45.70 481.426 3.49 0.00104 61706.7
17 517 2449.4 50.64 511.516 3.52 0.00098 71295.3
18 547 2444.3 55.74 541.071 3.55 0.00092 81578.8 85552.0
19 578 2438.8 61.16 571.130 3.58 0.00088 92968.2
20 608 2433.2 66.84 601.190 3.60 0.00083 105323.
21 638 2427.2 72.75 631.249 3.63 0.00079 118681.
22 669 2421.1 78.92 661.309 3.65 0.00076 133076.
23 699 2414.7 85.32 691.369 3.67 0.00072 148544.
24 730 2408.0 91.98 721.428 3.70 0.00069 165119. 175414.0
Reservoir Eng Hndbk Ch 10 2001-10-25 14:23 Page 706

Fetkovich’s Method
Fetkovich (1971) developed a method of describing the approximate
water influx behavior of a finite aquifer for radial and linear geometries.
In many cases, the results of this model closely match those determined
using the van Everdingen-Hurst approach. The Fetkovich theory is much
simpler, and, like the Carter-Tracy technique, this method does not
require the use of superposition. Hence, the application is much easier,
and this method is also often utilized in numerical simulation models.
Fetkovich’s model is based on the premise that the productivity index
concept will adequately describe water influx from a finite aquifer into a
hydrocarbon reservoir. That is, the water influx rate is directly propor-
tional to the pressure drop between the average aquifer pressure and the
pressure at the reservoir/aquifer boundary. The method neglects the
effects of any transient period. Thus, in cases where pressures are chang-
ing rapidly at the aquifer/reservoir interface, predicted results may differ
somewhat from the more rigorous van Everdingen-Hurst or Carter-Tracy
approaches. In many cases, however, pressure changes at the waterfront
are gradual and this method offers an excellent approximation to the two
methods discussed above.
This approach begins with two simple equations. The first is the pro-
ductivity index (PI) equation for the aquifer, which is analogous to the PI
equation used to describe an oil or gas well:
where e
w
= water influx rate from aquifer, bbl/day
J = productivity index for the aquifer, bbl/day/psi
p
–
a
= average aquifer pressure, psi
p
r
= inner aquifer boundary pressure, psi
The second equation is an aquifer material balance equation for a con-
stant compressibility, which states that the amount of pressure depletion
in the aquifer is directly proportional to the amount of water influx from
the aquifer, or:
where W
i
= initial volume of water in the aquifer, bbl
c
t
= total aquifer compressibility, c
w
+ c
f
, psi
−1
p
i
= initial pressure of the aquifer, psi
f =θ/360
WcWppf
etiia
=−( ) (10 - 37)
e
dW
dt
Jp p
w
e
ar
==−( ) (10 - 36)
Water Influx 707
Reservoir Eng Hndbk Ch 10 2001-10-25 14:23 Page 707
