Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications
Подождите немного. Документ загружается.


354 Useful Mathematical Formulas
cos(—#)
—
cos(2?r
—
9) = cos#
sin(7r ±9) =
=p
sin
9
cos(7r ± 9) =
—
cos#
7T
cos(- ±9) = Tsin0
7T
sin(
—
±0) = cos#
cos(^±0) = ±sin0
sin(— ±9) =
—
cos#
sin(A ± B) = sin A cos
JB
± cos A sin
JB
cos(A ± JB) = cos A cos B
=p
sin
^4
sin B
a mod 6 = o
—
b\a/b\,
&
7^ 0
sin
2
a; = -
(1 —
cos 2x)
£1
sin
3
x = -
(3
sin
a;
—
sin 3x)
sin
4
x = - (cos
4a;
- 4 cos 2x + 3)
sin
5
x = — (sin
5a;
-
5
sin
3a;
+ 10 sin x)
16
cos
2
x
—
-(1 + cos 2a;)
cos
3
x — -
(3
cos x + cos 3a;)

Useful Mathematical Formulas 355
cos
4
x = -
(cos
4a;
4- 4 cos
2a;
+ 3)
8
cos
5
x = — (cos
5a;
+
5
cos
3a;
+ 10 cos x)
16
sin
3a;
= 3 sin
a;
—
4 sin
3
x
sin
4a;
= cos x
(4
sin x
—
8 sin
3
a;)
sin 5x =
5
sin x
—
20 sin
3
x + 16 sin
5
x
cos
3a;
= 4 cos
3
x
—
3 cos x
cos
4a;
= 8 cos
4
x - 8 cos
2
a;
+ 1
cos 5x =
5
cos
a;
—
20 cos
3
a; + 16 cos
5
x
sin x ± sin y =
2
sin —-— cos —-—
x + y x
—
y
cos x + cos y = 2 cos —-— cos —-—
A Ad
. x+y . x-y
cos x
—
cos y = —
2
sin —-— sin —-—
„
in
-i
T
_ x x
3
(l)(3)a;
5
(l)(3)(5)a;
7
(1)
+
(2)(3)
+
(2)(4)(5)
+
(2)(4)(6)(7)
+
'''' * <
-l
^ • -l
cos a; =
— —
sin x, x < 1
e -l + (ja;)+
2
!
+
3!
+
4!
+ +
(r)!
+
COfl
(
af
) = l_* +*_...+ (_l)ri!_
2!
4!
v
' (2r)l
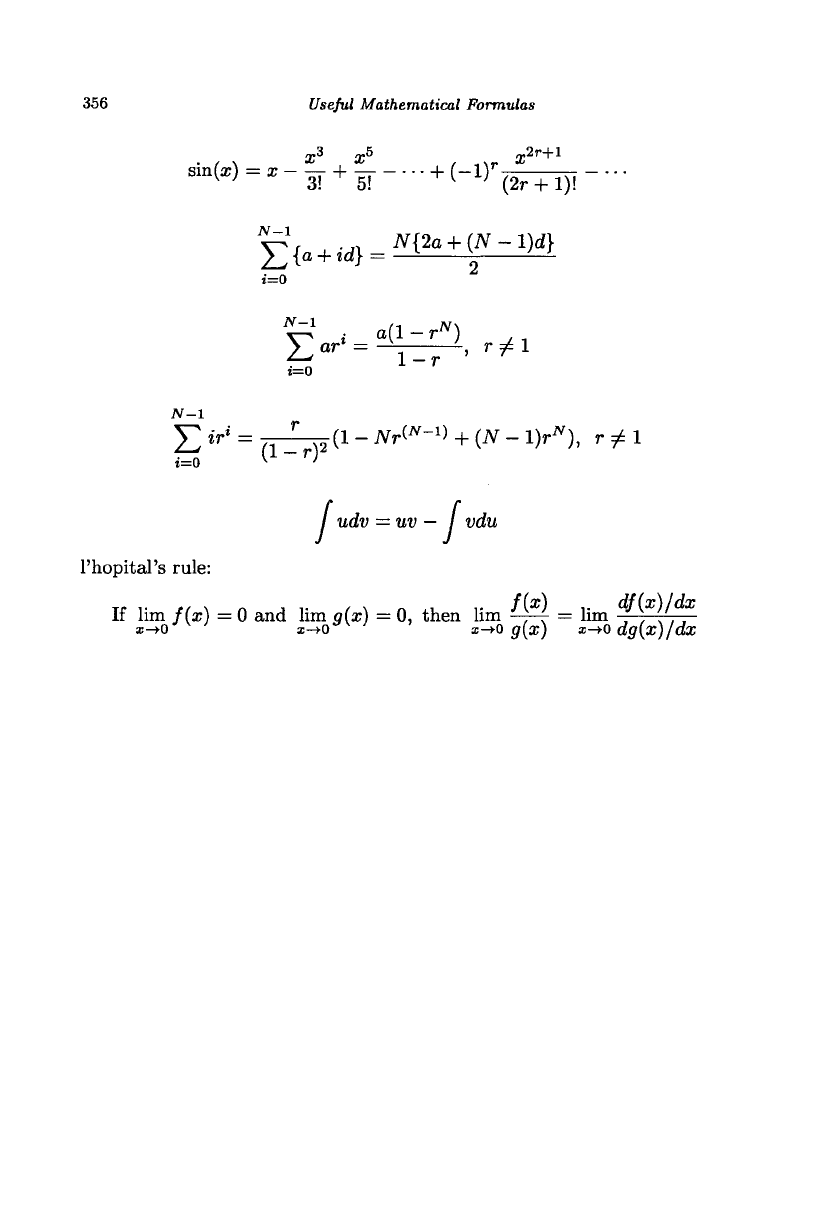
356
Useful Mathematical Formulas
X
3
X
5
, _
X
2r+1
sin(x) = x- — + — + (-l)
r
3!
5!
v
' (2r + l)!
JV-1
i=0
JV-1
J,_1
ci JV\
JV-1
»=0 ^ '
/ udv = uv
—
I vdu
l'hopital's
rule:
If lim f(x) = 0 and lim g(x) = 0, then lim ^ = lim
d
/^\/ff

Answers to Selected Exercises
2.1.2. A =
7.1,
w
= | radians/sample, / = ^ = n cycles/sample, period
= 12 samples, 0 = | radians.
2.2.3. 3cos(fn+ f).
2.3.6. |cos(fn)-3^sin(fn).
2.4.5.
^cos(fn+^).
2.5.3.
5.6283 cos(fn-0.2818)
2.6.4. The function is periodic with a period of 43.
2.7.2. sin(i|^n - f), - sin(^n + f), sin(^n - f)
2.8.1.
The fundamental cyclic frequency is ^. The first sinusoid is the
39th harmonic and the second is the 35th harmonic.
2.9.2. The amplitude of the spectral value at w = f is 2 and the phase is
—
j.
The amplitude of the spectral value at u =
—
f is 2 and the phase is
4-
The complex spectral coefficient at u = | is \/2
—
jy/2 and at u —
—
| is
y/2
+ jy/2.
3.4.2. dc=0.25, 3cos(^fn+ £), -0.25cos(7rn).
3.8.2. X(k) =
Wf
2k
,
k =
0,1,...,
7.
3.11.
X{2) = 16(2*1 -if).
3.13.
X(fc) =
1+e
-J^ll^fr*) (
1
~ ^(cos(^fc) + j sinffifc)))-
357

358
Answers to Selected Exercises
3.15.5. x(
n
) = £co6(fjp5n-a?0.
4.2.1.
X(k) = {6 +
J2,
-1 -j3,-2-jl2,l-j3}. X(23) = X(3) = 1 -j3,
X(-47) = X(l) = -1 - j3
4.3.2.
{2 +
j'3,
-1 - jl, -3 + jl, -2 + j2}.
4.6.3.
Odd half-wave. X(k) = {0, -2 - j4, 0, -2 + j4}.
4.7.2.
Odd half-wave and odd. X(k) = {0,
-8,0,8}.
4.8.1.
Odd half-wave and odd. X(k) = {0, -4 - j2,0,4 + j2}.
4.12.
{13,3,9,23}.
4.15.1.
y
xh
(n)
= {10,11,20,31}. y
hx
= {10,31,20,11}.
4.23.1.
The sum of \x{n)\
2
is 45. The sum of \X(k)\
2
/4 is also 45.
5.1.2. The input vectors are {(4 +j3, -jl), (2 - j5, jl)}. The DFT vectors
are{(6-j2,2+j8),(l-jl,-l-jl)}. The DFT X(fc) is {6-j2,l-jl,2+
j8,-l-jl}.
5.5.
The input vectors are {(1 + j5, -3 - jl), (-5 +
j2,1)}.
The output
vectors are {(—4 + jl, 6 + j3), (—3
—
j2,
—3)}.
When real and imaginary
parts are swapped, we get x(n) as {7
—
j4,
—2 —
j'3,3 + j6, —
j3}/4.
5.9. The swapped input vectors are {(j'4, -6- j2),
(2
+ jA,-4 + j2), (-5 +
j4,-l),(j4,-8)}.
The vectors after Stage 1 are {(2 + j8, -2), (-4 + j2, -8 - j6), (-5 +
j8,-5),(-l +
j8,-l-j8)}.
The output vectors are {(-3 +jl6,7), (0.9497 +
j'8.364,
-8.9497-j'4.364),
(-2 + j5, -2 - j5), (-12.9497 + jO.364, -3.0503 - J12.364)}. To get the
IDFT, the real and imaginary parts must be swapped and divided by 8.
5.10. The input vectors are {(3 - j6, -1 - j2), (3,1 - j6), (2 - j2,0), (4 -
A-J6)}.
The vectors after Stage 1 are {(5 - j8,1 - ji), (7 - j2, -1 + j2), (-1 -
j2,
-1 - j2), (-7.7782 - jO.7071,0.7071 - J9.1924)}.
The output vectors are {(12 -
j'10,
-2 - jQ), (3 - j3, -1 - ;5), (-8.7782 -
J2.7071,6.7782 - jl.2929), (-10.1924 - J2.7071,8.1924 - jl.2929)}. The
output vectors must be swapped to get the DFT values in natural order.

Answers to Selected Exercises
359
10.7(d). X(14,0) = -640(\/3-jl)
10.7(f).
X(8,6) = 512(V5 - jl), X(24,26) = 512(V5 + jl)
10.8(f).
x{n
1
,n
2
) = ^ cos(ff(2m +3n
2
) + f)
10.8(1).
x{n
u
n
2
) = ^
e
i(?f(
2
"i+
2
"=)-f)
10.11.
JST(7,21) = X(3,l) = -5 + jl,X(-4,-3) = X(0,1) = 4 + j6,
X(l,-3) = X(l,l) = -5+j3
10.16.
-> k
2
24 4 + j6 4 4-j6 "
3+jl -5 + j3 -1+jl -5 - jl
1
^ 6 2-j2 2 2 + j2
. 3-jl -5 + jl -1-jl
-5-J3.
10.18.
JV-1 N-l JV-1 JV-1
4
* E E l*(ni,n
2
)|
2
= E E |*(*i,fe>)|
2
=896
ni=0n
2
=0 fei =0*2=0
11.1(c).
Minimum
AT
= 14. X{7) = 28
N = 4. X(l) = 4 and A"(3) = 4
JV = 8. Jf (1) = 8 and X(7) = 8
iV = 16. X{7) = 16 and X(9) = 16
JV = 32. X(7) = 32 and X(25) = 32
11.2(b).
X
rect
{k)
= {I,l+j0.65,l+j2.61,l-j2.18,l,l+j2.18,l-j2.61,
l-jO.65}
XtriW = {0,-j0.14,jl.58,-jl.55,0,jl.55,-jl.58,j0.14}
X
han
{k)
= {0,-j0.33,jl.69,-jl.74,0,jl.74,-jl.69,j0.33}
X
ham
(.k)
= {0.08,0.08 - jO.25,0.08 + jl.76,0.08 - jl.78,0.08,0.08 +
jl.78,
0.08 - j
1.76,0.08+
J0.25}
11.3.
Zero-padding is not required since the frequency increment obtain-
able with the given record length T = 0.1 seconds, —^ = 10 Hz, is lower
than the required frequency increment, 20 Hz. Since sampling frequency

360
Answers to Selected Exercises
must be more than twice the highest frequency, the sampling period T
s
must be less than
2x
g
000
= 0.0001 seconds. Therefore, the number of sam-
ples,
N, in the time-domain data must be more than £- =
0
°p
01
= 1000.
Note that, in practice, typically two times the minimum N is used. In this
case,
2000 samples may be used. In addition, N is usually fixed to the next
largest power of two, so that a power of two DFT algorithm can be used.
The suggested value for N is, therefore, 2048. Note that, with increased
JV from the minimum value, we can decrease the frequency increment, or
increase the sampling frequency, or both as required.
12.4.
, , A A, . 2?r 1 . 2TT 1 . „2TT
x{t) = - - -(sin—i+ -sin2—i+ -sin3—i+ •••)
With A = 1 and T = 1, we get
x(t) = (sin(27ri) + - sin2(27rf) + - sin3(27rt) +
• •
•)
2 7r 2 3
A comparison of the FS and DFT coefficients is shown in Table 18.1.
Table 18.1 Comparison of the exact values of
X
c
(k),X
a
(k),
k =
0,1,...
,8 (second
row) with those obtained from the DFT coefficients with N = 4 (third row), N = 8
(fourth row), and N
—
16 (fifth row).
0
0.5
0
0.5
0
0.5
0
0.5
0
1
0
-0.3183
0
-0.25
0
-0.3018
0
-0.3142
2
0
-0.1592
0
0
0
-0.125
0
-0.1509
3
0
-0.1061
0
-0.0518
0
-0.0935
4
0
-0.0796
0
0
0
-0.0625
5
0
-0.0637
0
-0.0418
6
0
-0.0531
0
-0.0259
7
0
-0.0455
0
-0.0124
8
0
-0.0398
0
0
12.11.
2Aw 2A,. ,2ir . ,2-K . 1 . .2TT , ,
n
27r.
x(t) = — + — (sm(—w) cos(—t) + - sin(—2tu) cos(2—t)
1
. ,27T , ,2-K .
+-sin(—3w)cos(3—f) + ---)

Answers to Selected Exercises
361
With A = 1, T = 1 and w = |, we get
1 2 7T 1 7T 1 37T
#(*) = T + —(sin
—
cos(27rt) + - sin
—
cos 2(27r£) + - sin —- cos 3(27rf)
H
)
4 7r 4 2 2 3 4
A comparison of the FS and DFT coefficients is shown in Table 18.2.
Table 18.2 Comparison of the exact values of
X
c
(k),X
a
(k),
k =
0,1,...
,8 (second
row) with those obtained from the DFT coefficients with N = 4 (third row), N = 8
(fourth row), and N = 16 (fifth row).
0
0.25
0
0.25
0
0.25
0
0.25
0
1
0.4502
0
0.5
0
0.4268
0
0.4444
0
2
0.3183
0
0.25
0
0.25
0
0.3018
0
3
0.1501
0
0.0732
0
0.1323
0
4
0
0
0
0
0
0
5
-0.09
0
-0.0591
0
6
-0.1061
0
-0.0518
0
7
-0.0643
0
-0.0176
0
8
0
0
0
0
12.18.
X
e
,(0,0) = 2.5
Xc(ki,0) = •£-, *i=±l,±2,...
Z"KK\
-Y
c
.(0,*a) = 4-> fe = ±l,±2,...
7TK2
A comparison of the FS and DFT coefficients is shown in Table 18.3.
13.5.
sin(o;
- 10) sin(w + 10)
(u)
- 10) (w + 10)
Table 18.4 gives a comparison of the exact FT samples and those computed
by DFT.
13.8.
wi \ 2
™=(^y(^)

362
Answers
to
Selected Exercises
Table 18.3 Thesecond row ofthe first half of the table shows the exact
X
C3
(ki,0),
k\
—
0,1,...,8.
The
third, fourth,
and
fifth rows show those computed
by the DFT
with
4
x 4, 8 x 8, and 16 x 16
samples, respectively.
The
second half
of the
table shows
X
c3
(0,k
2
),
*
2
=0,l,...,8.
0,0
1,0 2,0
2.5 J0.4775 jO.2387
2.5 j'0.375
0
2.5 jO.4527 jO.1875
2.5 jO.4713 jO.2263
0,0
0,1 0,2
2.5 j'0.3183 jO.1592
2.5 J0.25
0
2.5 jO.3018 jO.125
2.5 jO.3142 jO.1509
3,0
jO.1592
jO.0777
jO.1403
0,3
jO.1061
jO.0518
jO.0935
4,0
5,0
jO.1194 j'0.0955
0
jO.0937 j'0.0626
0,4
0,5
j'0.0796 j'0.0637
0
j"0.0625 jO.0418
6,0
jO.0796
J0.0388
0,6
jO.0531
jO.0259
7,0
8,0
j/0.0682 jO.0597
jO.0186
0
0,7
0,8
jO.0455 j'0.0398
j'0.0124
0
Table
18.4 The
first row shows
the
first
8
samples
of
Xf
t
(u) computed
by
DFT with
T
=
16
and N =
1024. The second row shows the corresponding exact values.
-0.1086
-0.0979 -0.0679 -0.0236 0.0271 0.0749 0.1110 0.1277
-0.1088
-0.0982 -0.0680 -0.0237 0.0270 0.0750 0.1111 0.1278
Table
18.5 gives a comparison of the exact FT samples and those computed
by
DFT.
Table
18.5 The
first half
of the
table shows
the
first
4x4
samples
of
Xft(wi,U2)
computed
by DFT
with Ti,T
2
= 4 and
N
lt
N2
= 64. The
second half shows
the
corresponding exact values.
1
0.8112
0.4066
0.0907
0.8112
0.6581
0.3298
0.0736
0.4066
0.3298
0.1653
0.0369
0.0907
0.0736
0.0369
0.0082
1
0.8106 0.4053 0.0901
0.8106 0.6570 0.3285 0.0730
0.4053 0.3285 0.1643 0.0365
0.0901 0.0730 0.0365 0.0081

Answers to Selected Exercises
363
14.3.
14.7.
y(ni,n
2
) =
2/(ni,n
2
) =
4
8
-1
-2
8
18
1
-6
8
26
12
-7
6
26
20
-1
13
25
15
1
21
29
3
-7
15
26
-1
-12
5
12
1
-6
15.2.
X
c
t(ki,k2)
—
11.25
1.33
-2.25
-1.36
1.52
0.09
-2.06
-2.05
-1.75
-1.06
0.75
0.71
-0.90
-2.55
2.21
-3.09
16.2.
The values after the vector formation stage are
(30,32),
(10,8), (2,0), (-2,0), (-6, -8), (-18,0), (6,16), (-6,0)
The values after Stage 1 are
(24,36),
(-8,28), (8, -4), (-8,4), (24,40), (8,8), (16, -16), (0,0)
The values after Stage 2 are
(32,16),
(-16,0), (32,40), (32,24), (40,8), (8,8), (24,56), (8,8)
The output values are
(16,48),
(16,16), (64,0), (64,16), (48,32), (16,0), (32,16), (64,48)
The output values are to be divided by 16, the transform length.
