Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications

Подождите немного. Документ загружается.

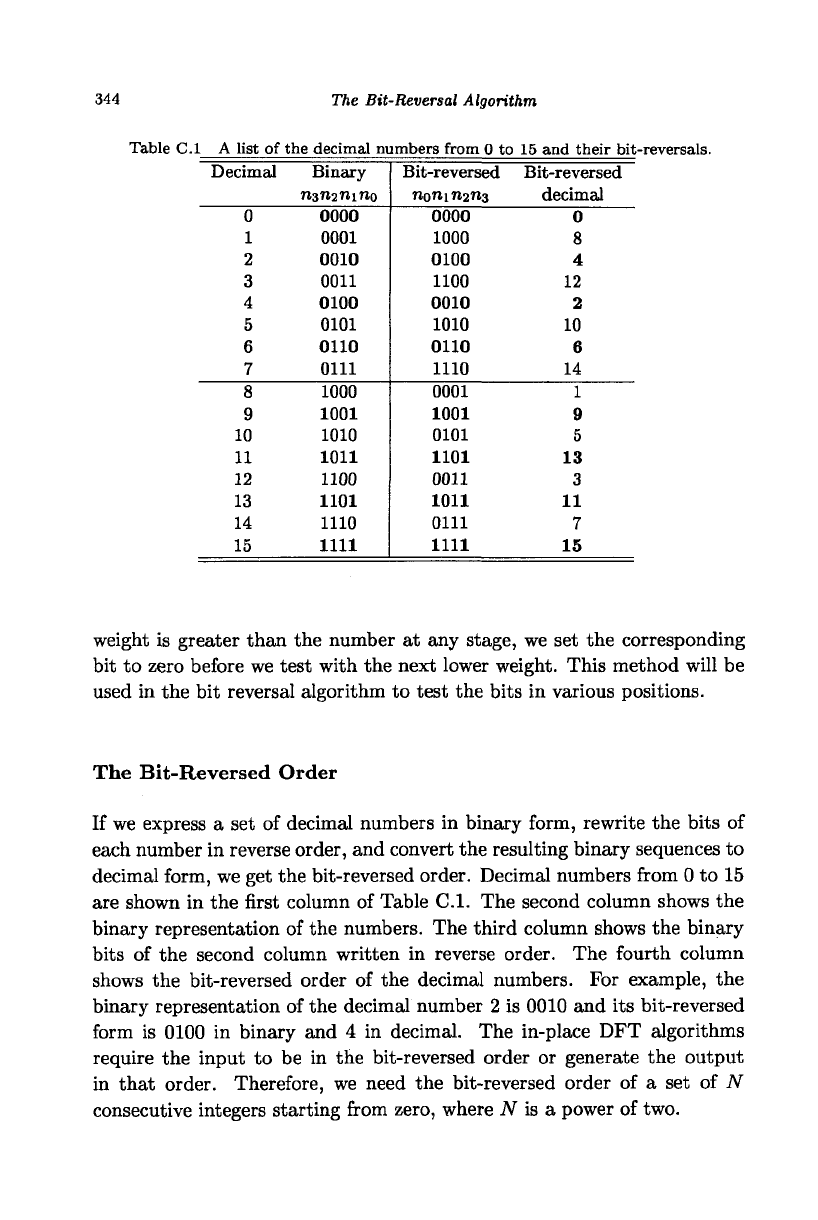
344 The Bit-Reversal Algorithm

Table C.l A list of the decimal numbers from 0 to 15 and their bit-reversals.

Decimal

Binary

ri3n2Tiino

0000

0001

0010

0011

0100

0101

0110

0111

1000

1001

1010

1011

1100

1101

1110

1111

Bit-reversed

noT»lTl2«3

0000

1000

0100

1100

0010

1010

0110

1110

0001

1001

0101

1101

0011

1011

0111

1111

Bit-reversed

decimal

weight is greater than the number at any stage, we set the corresponding

bit to zero before we test with the next lower weight. This method will be

used in the bit reversal algorithm to test the bits in various positions.

The Bit-Reversed Order

If we express a set of decimal numbers in binary form, rewrite the bits of

each number in reverse order, and convert the resulting binary sequences to

decimal form, we get the bit-reversed order. Decimal numbers from 0 to 15

are shown in the first column of Table C.l. The second column shows the

binary representation of the numbers. The third column shows the binary

bits of the second column written in reverse order. The fourth column

shows the bit-reversed order of the decimal numbers. For example, the

binary representation of the decimal number 2 is 0010 and its bit-reversed

form is 0100 in binary and 4 in decimal. The in-place DFT algorithms

require the input to be in the bit-reversed order or generate the output

in that order. Therefore, we need the bit-reversed order of a set of N

consecutive integers starting from zero, where JV is a power of two.

The Bit-Reversal Algorithm

345

The Bit-Reversal Algorithm

The complexity of finding the bit-reversed order is reduced by using the

similarities in the bit patterns of the numbers. We can easily observe the

following similarities in the bit-patterns of the list of binary numbers shown

in Table C.l. (1) The bit-reversal of odd numbers in the first half of the

list (1,3,5,7) are the even numbers (8,12,10,14) in the second half of the

list, because odd numbers have lsbs 1 and since they are in the first half

their msbs are zero. Therefore, in the bit-reversed form, they have their

msbs 1 and lsbs 0. For example, the bit-reversal of

0001

is 1000. Therefore,

the bit-reversal of the even numbers in the second half of the list need

not be found. (2) Since the only difference between an even number and

the next odd number is in the lsb, lsb 0 for even number and 1 for odd

number, once the bit-reversal of an even number is found the bit-reversal

of the next odd number is deduced by adding y to the bit-reversal of the

even number (setting the msb of the bit-reversal of the even number). For

example, the bit-reversal of 4 and 5 are, respectively, 2 and 10. Therefore,

the bit-reversals of (1,3,5,7) need not be found directly. With these two

observations, the problem of finding the bit-reversal of the set of 16 numbers

reduces to finding the bit-reversal of the four even numbers (0,2,4,6) in

the first half and those of the four odd numbers (9,11,13,15) in the second

half of the list. (3) Notice that the bit-patterns of these numbers in the two

halves of the Table C.l are the same except for the lsbs and msbs shown in

boldface. The bit-reversals of the odd numbers can be found from those of

the even numbers by simply adding ^ + 1 to the bit-reversals of the even

numbers. For example, the bit-reversal of 11 is found by adding 9 to the

bit-reversal of 2, which is 4, to get 13. Therefore, the list of numbers for

which the bit-reversals have to be found directly is further reduced to the

first four even numbers (0,2,4,6).

While we can keep on reducing the list by using the similarity in bit

patterns, we do not go any further for the following two reasons: (i) program

code becomes longer and (ii) coupled with the fact that we need only ^ bit-

reversals for an AT-point DFT with vector length two, the problem reduces

to the finding of only y bit-reversals directly. The execution time for

this operation is a negligible fraction of the execution time of the DFT

algorithms.

To find the bit-reversals of the first four even numbers, we use the bit-

reversal of the previous even number to find the bit-reversal of the current

346 The Bit-Reversal Algorithm

even number. We can obtain the next even number from an even number

by just adding the binary number 0010. This addition results in the change

of bits from 1 to 0, starting from the second bit from the right, until the

first zero bit is found, which is changed from 0 to 1 leaving the other bits

unchanged. Therefore, given the bit-reversal of a number, we have to start

from the second bit from the left and change all the 1 bits to zeros and the

first zero bit to 1, and leave the rest of the bits unchanged. For example,

the bit-reversal of the number 0100 is 0010. The bit-reversal of 0110 is

0110.

In the implementation of the algorithm, we use decimal numbers

and a 1 or 0 is found by comparing the number with appropriate weights.

For the example of finding the bit-reversal of 6, we compare the number 2

(bit-reversal of 4) with 4 and find that the second bit from the left is zero

(number is less than the weight). We change that bit to 1 (by adding the

weight 4) to get the bit-reversal as 6. The flow chart of the algorithm is

shown in Fig. 6.10(d).

Reference

(1) Sundararajan, D., Ahmad, M. O. and Swamy, M. N. S. (1994) "A

Fast Bit-Reversal Algorithm", IEEE Trans. Cir. and Sys. II, vol.

CAS-41,

No.10, pp. 701-703.

Appendix D

Prime-Factor DFT Algorithm

For most applications, we will be using the PM algorithms with a vector

length of 2. When N is not an integral power of 2, we use vectors of

length such as 6, 10, 14, etc. While the two-point DFT is the fundamental

operation in the algorithm, however, we need to compute DFTs of lengths

such as 6, 10, and 14, etc., in the vector formation stage. These DFTs are

computed efficiently by prime-factor algorithm. The SFG for computing

the DFT of six data points is shown in Fig. D.l. This algorithm requires

8 real multiplications and 36 real additions for the computation of a 6-

point complex DFT. The trace of the algorithm to compute the DFT of

Fig. D.l The prime-factor DFT algorithm, with N = 6, and its trace.

347

348 Prime-Factor DFT Algorithm

{1,3,5,2,4,6} is also given in Fig. D.l. For computing a 3-point DFT, use

the upper half of the SFG without the last stage. The input values x(2)

and a;(4) become, respectively, ar(l) and x(2).

Reference

(1) Burrus, C. S. and Parks, T. W. (1985) DFT/FFT and Convolution

Algorithms, John Wiley, New York.

Appendix E

Testing of Programs

In this Appendix, we present a variety of test data sets and ways for testing

DFT programs. Once a program is written, it must be tested not only with

a variety of data but also for different data sizes. For example, a program,

written for data lengths of an integral power of 2, must be tested at the

least for N = 16, 32, 64, 128, 256, and 512.

Comparing with the Trace of the Algorithm

Using tested programs, make files of DFTs corresponding to random input

data of lengths N = 16, 32, 64, 128, 256, and 512. For small DFT lengths,

such as 16 and 32, have the trace of the algorithm also.

Once a new program is written, compile and eliminate any syntax errors

so that the program is running and gives some output. Compare the output

of the program for the random test data with the correct output, starting

with TV = 16. If the output is correct, keep testing up to at the least

N = 512. Now, we can be reasonably sure that the program is working.

Further, we can test for more lengths and use a variety of input signals.

If the program does not work for N = 16, start comparing the trace

of the program with that you have already. You should be able to deduct

the possible errors in input, vector formation, and the special and general

butterflies, and correct the program. Testing for N = 16 is easy as the

data size is small and will eliminate most of the errors, if not all. Now

test the output for other lengths. If necessary, comparison of traces for

N = 32 should eliminate all the errors. Again, we emphasize that testing

for lengths longer than 32 is required.

349

350

Testing of Programs

Use of Closed-Form Solutions

We have derived the 1-D and 2-D DFT of several signals in closed-form

and several problems have been suggested. The closed-form expressions of

these DFTs can be used for testing.

Use of Properties

We found that certain properties produce certain form of output as pre-

sented in Chapters 4 and 10. Construct input data sets with those prop-

erties and check that the output exhibits the anticipated property. For

example, if x(n) is real-valued data, the DFT is hermitian-symmetric. In

short, every property can be tested.

Use of Special Inputs

Certain inputs, which produce known outputs, can be used to test pro-

grams. For example,

(1) Combination of scaled and delayed impulses

(2) Constant input, c

(3) Alternating constant input,

(—l)"c

(4) All zeros input

(5) x(n) = e(

'£"

), with N even. The magnitude of the DFT,

\X(k)\,

of this signal is equal to y/N for all k.

(6) Combination of complex exponentials and sinusoids. In particular,

sinusoids with frequencies that are relatively prime to each other

and relatively prime to the DFT length. For example, with N = 16,

test with sinusoids with frequency indices 3 and 5.

Use of Certain Operations

(1) Find the DFT of data and compute the IDFT of the transform to

get back the data

(2) Carry out the convolution operation using the DFT and check the

results with that obtained by the direct method. In a similar way,

the correlation operation can also be used.

Number of Operations, Precision, and Execution Time 351

Number of Operations, Precision, and Execution Time

The DFT values must be checked for expected precision. Check always

that the number of operations required for a given data size is correct with

the theoretical values. Check that the execution time is reasonable for the

specific computer.

Appendix F

Useful Mathematical Formulas

±j0

=cos9±jsin9

cos 9 =

e»'

-e--»'«

sin 9 = —

sin

9 + cos

9 = 1

cos 19 = cos

9 - sin

9 = 2cos

0 - 1 = 1 -

sin

cos 0

2 sin A cos B = sin(A - B) + sin(A + B)

2 cos A sin B = - sin(A - B) + sin(A + B)

2 sin A sin B = cos(A - B) - cos(A + B)

cos

A cos B = cos(A - B) + cos(A + B)

sin(-0) = sin(27r - 9) = - sin

353