Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications
Подождите немного. Документ загружается.


314 Discrete Walsh-Hadamard Transform
where ni is the zth bit in the binary representation of n. The Isb is indicated
by the subscript 0. The transform coefficients,
X
w
(k),
are called sequency
coefficients. Sequency is defined as, for waveforms with an odd number of
zero crossings, 0.5(number of zero crossings+1) and, for waveforms with an
even number of zero crossings, 0.5(number of zero crossings). The matrix
form of the defining equation, with N = 8, is written as
" MO) "
M(i)
M2)
M3)
M4)
M5)
M6)
. M?)
" 1 1 1 1
1
1 1 1 -•
1
1-1-1 j
1
1-1-1 -]
1-1 1-1 ]
1-1 1-1 -]
1-1-1 1 ]
1-1-1 1 -]
till"
1
-1 -1 -1
L
1-1-1
L
—1 1 1
L
-1 1-1
L
1 -1 1
L
-1 -1 1
L
1 1 -1_
" x(0) "
ar(l)
x(2)
*(3)
x(4)
*(5)
x{6)
. x(T) .
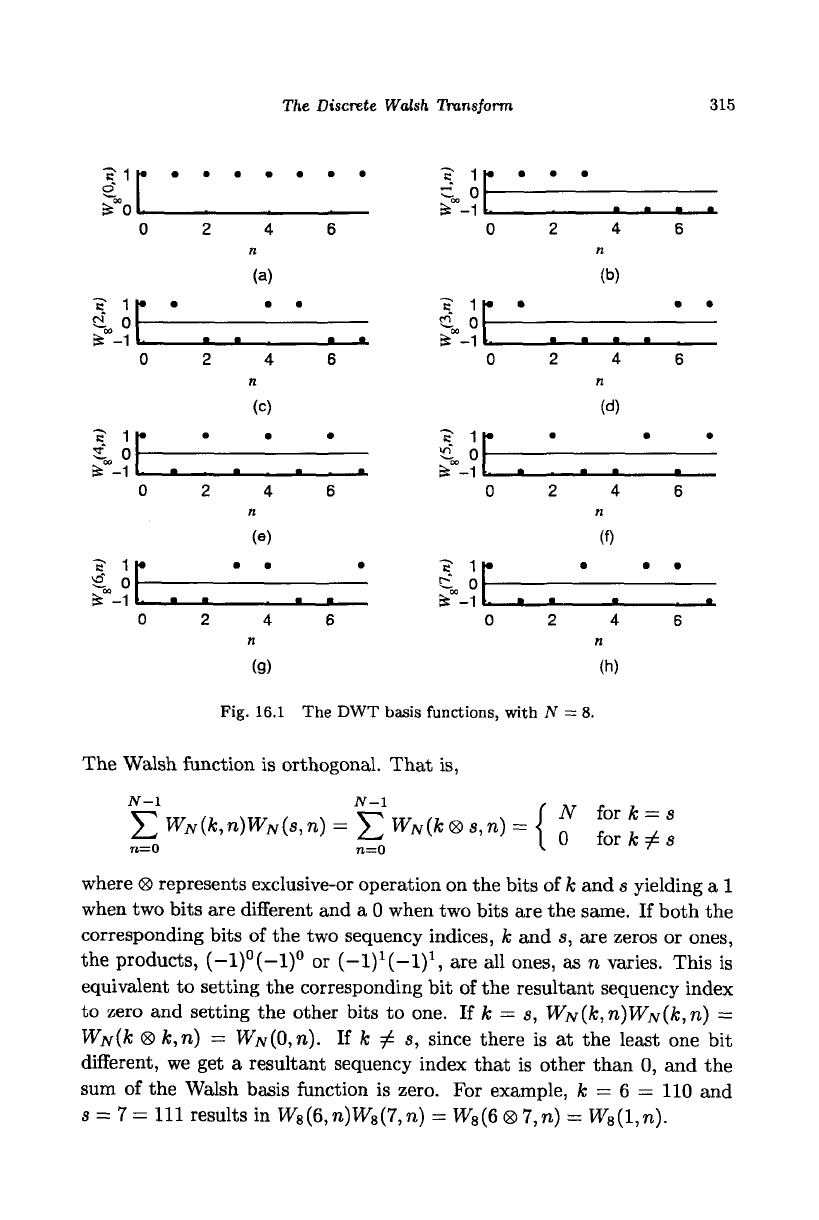
The DWT basis waveforms, with N = 8, are shown in Fig. 16.1. The DWT
basis functions,
Af-l
W
N
(k,n)=
J[{-l)
n
*
k
"-^,
n
,fc = 0,l,...,iV-l,
can be generated using the bits in the binary representation of n and k,
the data and sequency indices. For each value of k, multiplying the cor-
responding bits of n and k to get a 0 or 1 and finding the product of (-1)
to the power of 0 or 1 yields the kernel values. Let k = 3 = Oil and
n = 2 = 010. Then, the bit-by-bit product of 110 (remember the bits of
k are to be reversed) and 010 is 010. The corresponding kernel value is
W
8
(3,2) = (-1)°(-1)
1
(-1)° =
-1-
Since the first row of the kernel matrix
is all ones,
N-l
Y,W
N
(0,n)=N
n=0
Since there are equal number of plus ones and minus ones in all other rows,
JV-l
J2W
N
(k,n) = 0,
Jfc
=
1,2,...,JV-l
n=0
The Discrete Walsh Transform
315
l
1
r
fe°°oL
0
•?
11*
ci
o
fe
1
.
0
B-
1
S.
0
fe
1
•
•
_•_
2
•_
2
•
.
_*.
_•.
4
n
(a)
•
4
n
(o)
•
•
_•_
6
a—
6
•
_*L
_•.
"c
1
&
1
•
0
"B 1
t*
C
0
£
1
0
"B
1
!£
0
B£°°
1
•
•
•
—*_
•
2
•
2
•
•
•
4
n
(b)
•
•
4
n
(d)
_•
•-.
_a_
_•_
•
•
.
6
•
6
_•
_«.
•
•
(e)
?
1|« • • •
£
0
OO
I
*
-1 L—•—• . • •
(9)
B-
1f
cL
o -
fe
-1
L—•—•_
(f)
4
n
(h)
Fig.
16.1 The DWT
basis functions, with
N = 8.
The Walsh function
is
orthogonal. That
is,
N-l
JV-1 ,
n=0
n=0 ^
TV
for k = s
fork^s
where
<g>
represents exclusive-or operation
on the
bits
of k and s
yielding
a 1
when
two
bits
are
different
and a 0
when
two
bits
are the
same.
If
both
the
corresponding bits
of the two
sequency indices,
k and s, are
zeros
or
ones,
the products, (-1)°(-1)°
or
(-l^-l)
1
,
are all
ones,
as n
varies. This
is
equivalent
to
setting
the
corresponding
bit of
the resultant sequency index
to zero
and
setting
the
other bits
to one. If k = s,
Wjv(k,n)WN(k,n)
=
Wjv(fc
® k,n) =
Wjv(0,n).
If k ^ s,
since there
is at the
least
one bit
different,
we get a
resultant sequency index that
is
other than
0, and the
sum
of the
Walsh basis function
is
zero.
For
example,
k = 6 — 110 and
s
= 7 =
111 results
in
W
8
{Q,n)W
s
(7,n)
=
W
8
(6®
7,n) =
W
s
{l,n).

316
Discrete Walsh-Hadamard Transform
The inverse DWT is given by
1
N-i M-\
^)^E
I
«'WlI(-
1
)"
ifeM
"
I
'
i
'
n
= 0,l,...,iV-l
k=0 t=0
As the inverse DWT definition is similar to that of the DWT except for a
constant divisor, an algorithm for computing the DWT can be used directly
for computing the inverse DWT. The transform pair can be verified using
the orthogonal property.
Example 16.1 Let x(n) =
{1,3,5,7}.
Compute the DWT of x(n). Get
back x(n) by computing the inverse DWT of the sequency coefficients.
Solution
X
w
{0)
= 1 + 3 + 5 + 7 = 16
X
w
(l)
= 1 + 3-5-7 =-8
X
w
(2)
= 1-3 + 5-7 =-4
X
w
(3)
= 1-3-5 + 7 = 0
The inverse DWT is
x(0) = (16 + (-8) + (-4) + 0)/4 = 1
x(l) = (16 + (-8) - (-4) - 0)/4 = 3
x{2) = (16 - (-8) + (-4) - 0)/4 = 5
ar(3) = (16-(-8)-(-4) + 0)/4 = 7 I
The PM DWT algorithm
While it is possible to derive the algorithm from the definition, it is much
easier to deduce the algorithm from the 2 x 1 PM DIT DFT algorithm due
to the similarity in the definitions of the DWT and DFT. Consider the DFT
definition, with N = 4, given below.
3
X(fc) = ^x(n)W
4
"
fc
, it = 0,1,2,3
n=0
Representing the indices in the twiddle factor in terms of binary bits, we
get
3
n=0

The Discrete Walsh Transform
317
O
__
V^
x
(
n
\^
4
(™ifci)j^
2
("o*i+fconi)^l(n
0
fco)
n=0
3
r
l(n
0
fco)
= 5^ar(n)(-l)
(no
*
1+
*
oBl)
W4
n=0
This definition
is the
same
as
that
of the DWT if we set all the
twiddle
factors, except those with powers
of (—1), to
unity. Therefore,
by
setting
all twiddle factors
to
unity, except those with powers
of (-1), we
change
a
DFT algorithm
to a DWT
algorithm.
The PM DWT
algorithm
is
deduced
from
the 2x1 PM DIT DFT
algorithm
as
follows.
The
input vectors
a(ri)
are defined
as
N
N
o.(n)
=
{o
0
(n),a
1
(n)}
=
{(x(n)
+ x(n +
-j),x{n)
- x(n + y))},
N
n
= 0,l,...,--l
The output vectors
A(k) are
defined
as
A(k)
=
{A
0
(k),
At
(*)}
=
{X
w
(k),X
w
(k
+ y)}, k =
0,1,...,
y - 1
The equations characterizing
the PM DWT
butterfly
are
given
as
A[*
l
Hh)
=
4
r)
w-4
r)
w
4
r+1
>(Z)
=
A[
r
\h)
+ A<?\l)
A?
+1
\l)
=
A[
r
Hh)-A[
r
HD
The
SFG of the PM DWT
algorithm, with
N = 16, is
shown
in Fig. 16.2,
which
is the
same
as
that
of the 2x1 PM DIT DFT
algorithm with
the
twiddle factors
set
equal
to
unity.
The
number
of
real addition operations
required
by the PM DWT
algorithm
is N
log
2
N.
Example
16.2
Find
the
trace
of the
algorithm shown
in Fig. 16.2 for
the following input data.
{1,3,1,1,4,0,4,1,3,2,1,0,2,1,4,3}
Solution
The trace
is
shown
in Fig. 16.3. The
sequency coefficients
are

318
Discrete Walsh-Hadamard Transform
tage 1 stage 2 stage 3
o(7)o
A(0)
A(l)
A(2)
A(3)
A(4)
A{5)
A(6)
A(7)
Fig. 16.2 The SFG of the PM DWT algorithm, with N = 16.
{31,
-1, -7,1,1,1,11,
-5,9,1,
-9, -9, -1, -1, -3, -3}
The 2-D DWT
The 2-D DWT of an N x N image {x(n
u
n
2
), n
u
n
2
=
0,1,..
.,N - 1} is
denned as
7V-1 JV-1 M-l
ni=0 n2=0
M-l
I n
2
=0 i=0
M-l
x JJ (-l)^)'^)"-
1
-
1
, fci,fc
2
=0,l,...,iV-l
(=0
Example 16.3 Compute the 2-D DWT of the following matrix of data.

The Discrete Walsh Transform
319
X
(o)
m
x(8)
|_3j
*(1)
|~3
*(2)
m
z(10)LU
*(3)
m
a?(ll) I_QJ
x{4)
x(12)
x(5)
x(13)
x(6)
x(14)
*(7)
x(15)
Vector
Formation
and
Swapping
Stage
1
Output
4
-2
6
2
10
-2
0
-4
20
0
0
0
311
-MO)
9j X
w
(&)
rri
^(i)
LU
-M9)
yy
^(io)
X
w
{3)
•Mil)
11 X«,(4)
l]
^(12)
rri
^(5)
LU
X
W
(U)
Til X
w
{6)
31 X„,(14)
X
w
(7)
-M15)
a
Fig.
16.3 The
trace
of the PM DWT
algorithm, with
N = 16.
The origin
is at
upper left-hand corner.
n
2
->
13
11
4
0 4 1
3
2 10
2
14 3
Solution
Computing
the 1-D DWT of the
rows,
we get
6
9
6
10
2
-1
4
-4
-2
7
2
2
-2
1
0
0

320
Discrete Walsh-Hadamard Transform
Computing the
1-D
DWT
of
the columns of the resulting matrix, we get
*1
I
"
31
-1
-7
1
k
2
-»•
1
1
11
-5
9
1
-9
-9
-1
-1
-3
-3
The original image
can be
obtained
by
computing
the 1-D row
inverse
DWTs
of
the transform matrix followed by the
1-D
column inverse DWTs
of the resulting matrix and vice versa.
I
It can
be
shown that
the
2-D computation
is
the same
as
that
of 1-D
DWT. As such the SFG
for
computing the 2-D DWT remains the same
as
in Fig. 16.2 except that
the
data length
is
iV
2
.
If
data
is
read row-by-row
from the input file,
the
output would
be
written column-by-column
and
vice versa.
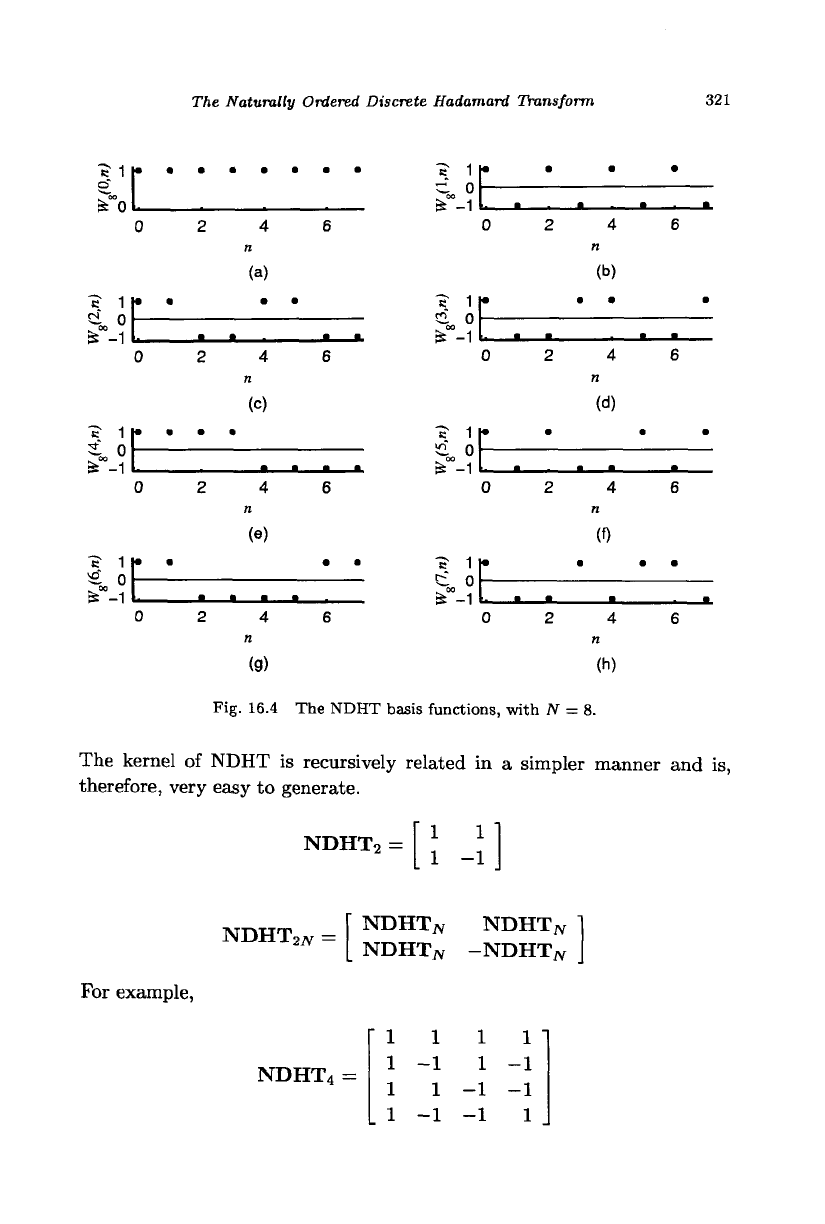
16.2 The Naturally Ordered Discrete Hadamard Transform
This transform generates
the
same sequency coefficients
as
that
of the
DWT, but
in
bit-reversed order. The NDHT of
a
data sequence {x(n),
n =
0,1,...,
N
—
1}
is
defined
as
Xnh(k)
= Y, *(n)(-l)^-°
Uii
>
fc =
0,1,...,
iV
-
1,
n=0
where
ni
is the ith bit
in
the binary representation of n, the lsb is indicated
E
Af-l
,
„., „^„„. -
,..,,,..,..,
v
-, i=o
niki
,
n,
k =
0,1,..., JV -1,
with
N =
8, are shown in Fig. 16.4. The matrix form
of the defining equation, with
N = 8, is
written
as
X
nh
(0)
X
nh
(l)
X
nh
(2)
X
n
h(3)
X
nh
(4)
X
n
h{5)
X
nh
(6)
L
X
nh
(7)
"111111
1-1
1-1 1-1
1
1-1-1 1 1
1-1-1
1 1-1
1
1 1 1-1-1
1-1
1-1-1 1
1
1 _1 -1 _1 _1
1-1-1
1-1 1
1
1"
1
-1
-1
-1
-1
1
-1
-1
-1
1
1
1
1
-1
• ar(0)
"
x(l)
x(2)
x(3)
x(4)
x(5)
x(6)
. «(7)
.
The Naturally Ordered Discrete Hadamard Transform
321
I
1
Bt"o
0
"e 1
^ 00
£ 1
• •
0
•? 11* •
€ o
fe 1 1
0
"c 1 t* •
€ 0
^
o°
1
0
2
2
•
2
•
2
4
n
(a)
• •
4
n
(c)
•
4
n
(e)
—a • a_
4
n
(g)
6
6
6
• •
6
"?
1
[•
d o—
^ oo 1
fe
iL_
0
"e
1
p
e o—
£ iL_
0
"B
1
p
£ 0—
•. 0° I
~s
1
L_
0
"c
1
p
£ 0—
fe iL
0
_a_
_a_
_•_
_•_
•
2
2
•
2
2
•
_a .
4
n
(b)
• •
4
n
(d)
_• •
4
n
(0
•
•_
4
n
(h)
_•_
_i_
•
•
•
6
•
•
6
•
6
•
. t
6
Fig. 16.4 The NDHT basis functions, with
AT
= 8.
The kernel of NDHT is recursively related in a simpler manner and is,
therefore, very easy to generate.
NDHT2 =
1 1
1 -1
NDHT
2)V
=
NDHTJV NDHTJV
NDHT
N
-NDHTJV
For example,
NDHT
4
1
1
1
1
1
-1
1
-1
1
1
-1
-1
1
-1
-1
1

322
Discrete Walsh-Hadamard Transform
By writing the rows of this kernel in bit-reversed order, we can get the
DWT kernel. The inverse NDHT is given by
^(») = T7 ]T X
nh
(*)(-l)2-«-o "•*••, n = 0,l,...,7V-l
fc=0
Example 16.4 Let x{n) =
{1,3,5,7}.
Compute the NDHT of x(n). Get
back x(n) by computing the inverse NDHT of the sequency coefficients.
Solution
X
nh
(0)
= 1 + 3 + 5 + 7= 16
Xnh(l) = 1-3 + 5-7=-4
X
nh
(2)
= 1 + 3-5-7 =-8
X
nh
(3)
= 1-3-5 + 7 = 0
The inverse NDHT is
x(0) = (16 + (-4) + (-8) + 0)/4 = 1
x(l) = (16 - (-4) + (-8) - 0)/4 = 3
x(2) = (16 + (-4) - (-8) - 0)/4 = 5
x(3) = (16 - (-4) - (-8) + 0)/4 = 7 I
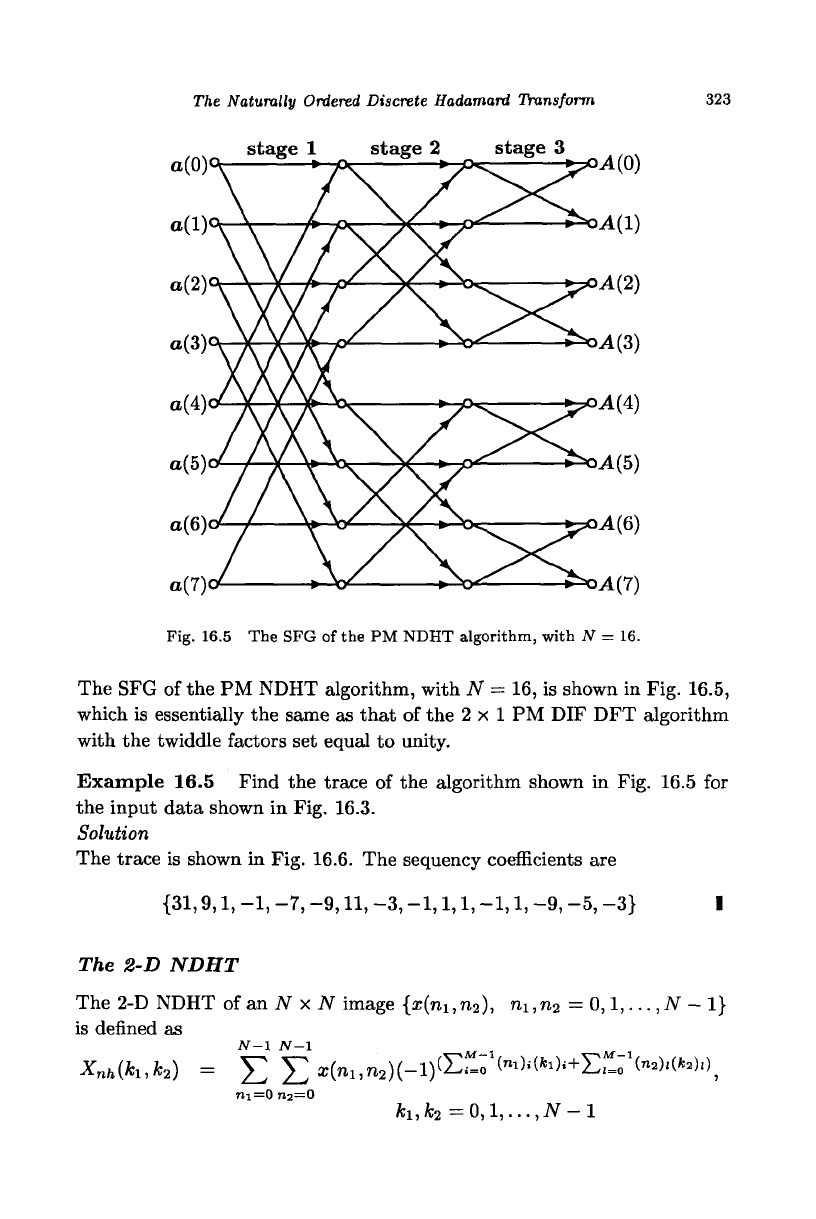
The PM NDHT algorithm
Since the NDHT produces the same coefficients as that of the DWT, but
in bit-reversed order, the PM NDHT algorithm is deduced from the 2x1
PM DIF DFT algorithm as follows. The input vectors a(n) are defined as
N N
o(n) = {a
0
(n),oi(n)} = {(x(n) + x(n
+—),x(n)
- x(n+—))},
N
n = 0,l,.-.,y-l
The output vectors A(k) are defined as
A(k) = {A
0
(k), Ax (k)} = {X
nh
(2k), X
nh
(2k + 1)}, k =
0,1,...,
y - 1
The equations characterizing the PM NDHT butterfly are given as
4
r+1)
w
=
<4
r)
w+4
p)
(o
o[
r+1)
(ft) = ai
r
\h)-a£\l)
a£
+1
\l) = a[
r
\h) + aP(l)
a[
r+1
)(Z) = a^iV-a^Hl)
The Naturally
Ordered
Discrete Hadamard Transform
stage 1 stage 2 stage 3
323
A(0)
A(l)
A(2)
Fig. 16.5 The SFG of the PM NDHT algorithm, with N = 16.
The SFG of the PM NDHT algorithm, with N = 16, is shown in Fig. 16.5,
which is essentially the same as that of the 2x1 PM DIF DFT algorithm
with the twiddle factors set equal to unity.
Example 16.5 Find the trace of the algorithm shown in Fig. 16.5 for
the input data shown in Fig. 16.3.
Solution
The trace is shown in Fig. 16.6. The sequency coefficients are
{31,9,1,
-1,
-7,
-9,11,
-3,
-1,1,1, -1,1,
-9, -5, -3} I
The 2-D NDHT
The2-D NDHT of an N x N image {x(m,n
2
), n
u
n
2
=
0,1,...
,N - 1}
is defined as
N-l
N-l
X
nh
(k
u
k
2
)
= Y, E *(ni,n
2
)(-l)
(
£
i=
; ("i)*(»0«+E^
1
(»»)'(fe)')
>
ni=0 ri2=0
k
u
k
2
=0,l,...,iV-l
