Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications

Подождите немного. Документ загружается.

284

The Continuous-Time Fourier Transform

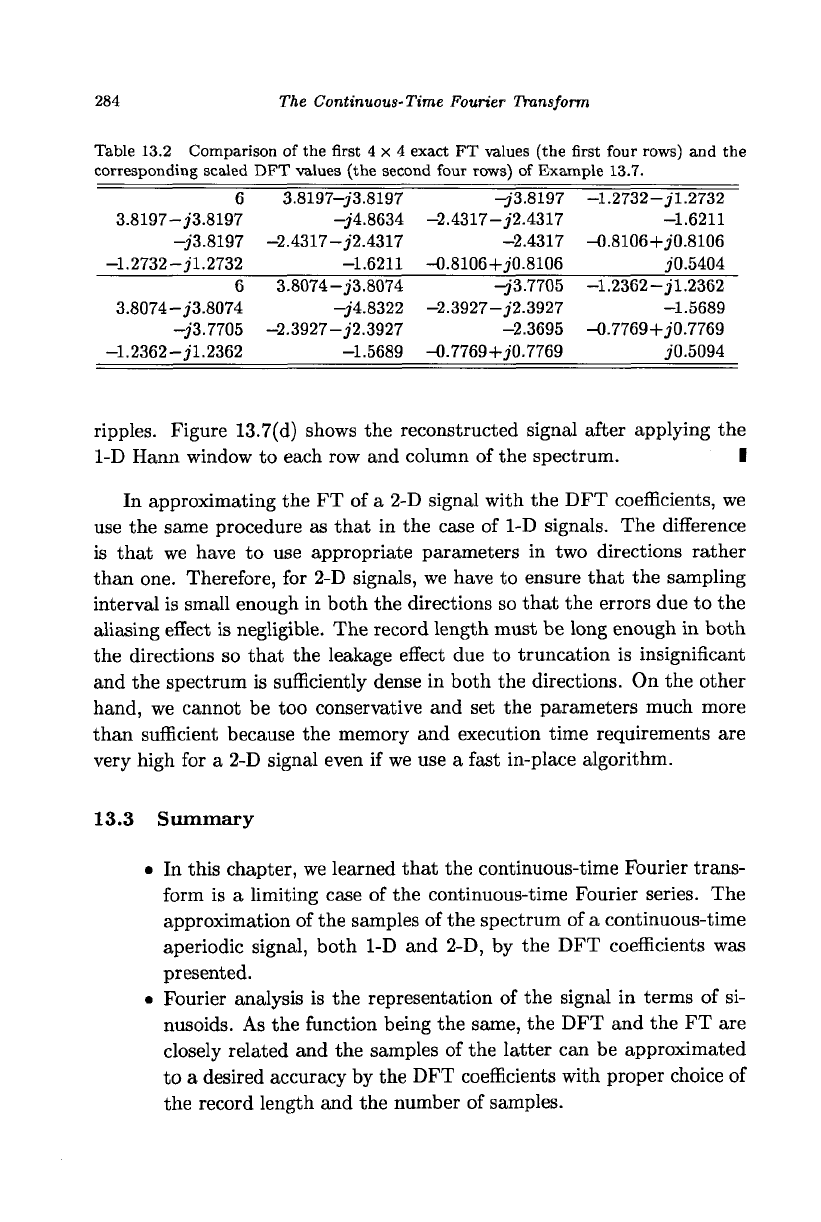
Table 13.2 Comparison of the first 4x4 exact FT values (the first four rows) and the

corresponding scaled DFT values (the second four rows) of Example 13.7.

3.8197-

-1.2732-

3.8074-

-1.2362-

-J3.8197

-jl.2732

-J3.8074

-J3.7705

-jl.2362

3.8197-j3.8197

-jf4.8634

-2.4317-j2.4317

-1.6211

3.8074-J3.8074

-j4.8322

-2.3927-j2.3927

-1.5689

^/3.8197

-2.4317-j2.4317

-2.4317

-O.8106+J0.8106

^3.7705

-2.3927-j2.3927

-2.3695

-0.7769-f-j0.7769

-l.2732-jl.2732

-1.6211

-0.8106+j0.8106

jO.5404

-l.2362-jl.2362

-1.5689

-0.7769+J0.7769

jO.5094

ripples. Figure 13.7(d) shows the reconstructed signal after applying the

1-D Hann window to each row and column of the spectrum. I

In approximating the FT of a 2-D signal with the DFT coefficients, we

use the same procedure as that in the case of 1-D signals. The difference

is that we have to use appropriate parameters in two directions rather

than one. Therefore, for 2-D signals, we have to ensure that the sampling

interval is small enough in both the directions so that the errors due to the

aliasing effect is negligible. The record length must be long enough in both

the directions so that the leakage effect due to truncation is insignificant

and the spectrum is sufficiently dense in both the directions. On the other

hand, we cannot be too conservative and set the parameters much more

than sufficient because the memory and execution time requirements are

very high for a 2-D signal even if we use a fast in-place algorithm.

13.3 Summary

• In this chapter, we learned that the continuous-time Fourier trans-

form is a limiting case of the continuous-time Fourier series. The

approximation of the samples of the spectrum of a continuous-time

aperiodic signal, both 1-D and 2-D, by the DFT coefficients was

presented.

• Fourier analysis is the representation of the signal in terms of si-

nusoids. As the function being the same, the DFT and the FT are

closely related and the samples of the latter can be approximated

to a desired accuracy by the DFT coefficients with proper choice of

the record length and the number of samples.

Exercises

285

References

(1) Guillemin, E. A. (1952) The Mathematics of Circuit Analysis, John

Wiley, New York.

(2) Cadzow, J. A. and Van Landingham, H. F. (1985) Signals, Systems,

and Transforms, Prentice-Hall, New Jersey.

Exercises

13.1 Find the FT analytically.

e~°-

cos(2i) + e-°'

* sin(3i) for 0 < t < oo

~ { 0 for t

Let the record length T

—

40 seconds and the number of samples N = 512.

Compute the samples of the spectrum of the signal using the DFT. Tabulate

the first 8 scaled DFT coefficients and the corresponding FT coefficients.

13.2 Find the FT analytically.

t)=

i —1*1 for |i| < 1

elsewhere

Let the record length T

—

32 seconds and the number of samples N = 512.

Compute the samples of the spectrum of the signal using the DFT. Tabulate

the first 8 scaled DFT coefficients and the corresponding FT coefficients.

13.3 Find the FT analytically.

x(t) = e~

Let the record length T = 8 seconds and the number of samples N = 256.

Compute the samples of the spectrum of the signal using the DFT. Tabulate

the first 8 scaled DFT coefficients and the corresponding FT coefficients.

13.4 Find the FT analytically.

x(t) = e"

4t2

Let the record length T = 8 seconds and the number of samples N = 256.

Compute the samples of the spectrum of the signal using the DFT. Tabulate

the first 8 scaled DFT coefficients and the corresponding FT coefficients.

286

The Continuous-Time Fourier Transform

* 13.5 Find the FT analytically.

\ _ / cos(lOi) for - 1< t < 1

\ 0 elsewhere

Let the record length T = 16 seconds and the number of samples N = 1024.

Compute the samples of the spectrum of the signal using the DFT. Tabulate

the first 8 scaled DFT coefficients and the corresponding FT coefficients.

13.6 Find the FT analytically.

u\ _ J

~* for 0 < t < oo

X[t)

~ { 0 for t < 0

Let the record length T = 8 seconds and the number of samples N = 64.

Compute the samples of the spectrum of the signal using the DFT. Tabulate

the first 8 scaled DFT coefficients and the corresponding FT coefficients.

13.7 Find the FT analytically.

. , e

_tl

-ta

for 0 <ti < oo, 0 < t

< oo

*&'**) "I o elsewhere

Let the record length Ti,T

= 8 seconds and the number of samples

Ni,N

— 128. Compute the samples of the spectrum of the signal using the

DFT. Tabulate the first 4x4 scaled DFT coefficients and the corresponding

FT coefficients.

* 13.8 Find the FT analytically.

(l-|*i|)(l-M) for|ii|<l,|i

|<l

' ' 0 elsewhere

Let the record length 7i,T

= 4 seconds and the number of samples

Ni,N% = 64. Compute the samples of the spectrum of the signal using

the DFT. Tabulate the first 4x4 scaled DFT coefficients and the corre-

sponding FT coefficients.

Chapter 14

Convolution and Correlation

The linear convolution operation, relating the input, output, and the im-

pulse response of an LTI system, is of fundamental importance. The op-

eration of linear correlation is very similar to convolution and is used as a

similarity measure between signals. Use of DFT makes the computation of

these very important operations more efficient than implementing directly.

In Sec. 14.1, the linear convolution operation is presented. In Sec. 14.2,

the computation of convolution using the DFT is described. In Sec. 14.3,

the overlap-save method of convolution of long sequences is explained. In

Sec.

14.4, the convolution of 2-D signals is presented. In Sec. 14.5, the

computation of correlation is described.

14.1 The Direct Convolution

In practice, the input signal to a system is usually arbitrary. The system

response is obtained by representing the input signal in terms of impulses,

finding the system response to each impulse, and adding all the responses.

It is required to measure the system response to only one signal, the impulse.

The reason for the selection of the impulse signal as the basic signal is that

it is a simple signal and it is easy to express a given arbitrary signal in

terms of impulses.

In the convolution operation, we express the present output as an ex-

clusive function of the present and all past input samples. Let us formulate

the convolution operation through an example. Assume that a savings ac-

count in a bank yields 10% of interest per year for deposit. If we deposit

$1 in the bank now, the money in the account next year will be 1.1$, the

287

288 Convolution and Correlation

\ i.i

-i)

h{2

l.l

-i)

h(3

1.1

l.l

-0

y(n)

30C

1.1

l.l

30C

1.1

20C

1.1

l.l

53C

l.l

1.1

583 641.3

Fig. 14.1 The linear convolution operation.

year after that it will be

1.1

etc. The savings account is a process and

the rate of growth of money of 1$ is the impulse response. Let us say

we open an account with a deposit of $300 and deposit another $200 at

the beginning of the next year. The deposits are the inputs. Let us try

to find the money, which is the output, in our account for the next three

years assuming that we make no other deposits or withdrawals in this pe-

riod and close the account after three years. At the beginning of this year,

the balance is $300 that we have deposited. At the beginning of the next

year the balance will be $300 x 1.1 + $200. The year after that the bal-

ance will be $300 x l.l

+ $200 x 1.1. After three years the balance will be

$300 x

l.l

$200 x l.l

. The problem of finding the balance can be formu-

lated neatly as shown in Fig. 14.1. The impulse response h(i),i = 0,1,2,3

{1,1.1,

l.l

The input x(i), i = 0,1,2,3 is {300,200,0,0}. The im-

pulse response when folded about the y-axis, h(0 - i), is {l.l

l.l

,1.1,1}.

To find the response

j/(0),

we simply find the sum of products of all the

overlapping samples of x{i) and h(0-i). Then, we shift h(0

—

i) to the right

by one position to get h(l

—

i). The sum of products of all the overlapping

samples of x(i) and /i(l - i) yields the output y(l). This process can be

continued to find the other two outputs. Note that the values of x(i) and

h(i) for all values of i not shown in Fig. 14.1 are assumed to be zero. We

get the same result if x(i) is folded rather than h(i).

In summary, given the input sequence x(i) and the impulse response of

a system h(i), there are four steps to find the output of the system through

the convolution operation. 1. Fold one of the sequences about the y-axis.

Shift the folded sequence to the point where the output response is to

be determined. 3. Multiply the overlapping samples of the two sequences.

Add all the products to find the output at that output point.

The Indirect Convolution

289

The linear convolution

The linear convolution operation is defined as follows. Let x(n),n =

0,1,...,

P - 1 and h(n),n =

0,1,...,

Q — 1 be two arbitrary sequences.

Assume that x(n) — 0, for n < 0 and n > P

—

1 and h(n) = 0, for n <

0 and n > Q

—

1. Then, the linear convolution of the two sequences is

defined as

Min(n,P-l) Min(n,Q-l)

) = 53 x{i)h{n -i)= ^2 h(i)x(n - i),

i=Max(0,n-Q+l) i=Max(0,n-P+l)

n =

0,l,...,P

+ Q-2

It is easy to see that the present output is the sum of products of the two

sequences, each other's index running in opposite directions.

14.2 The Indirect Convolution

Implementing the time-domain convolution by computing the DFT of two

signals, multiplying the DFTs term by term, and computing the IDFT of

the product is known as indirect convolution. The computational com-

plexity of the indirect convolution method, using a fast DFT algorithm, is

0(N log

N) compared with 0(N

) for the direct convolution.

The circular convolution

Let x(n) and h(n), n =

0,1,...,

TV —

1 be the samples of one period of

periodic signals with period iV. Then, the circular or periodic convolution

of the two sequences is defined as

N-l

y(n) = ^2 x(i)h(n - i) = J^ h(i)x(n -i), n = 0,1,. ..,N- 1

i=0 j=0

The values y(n),n =

0,1,...,

—

1 represent samples of one period of the

periodic output sequence y(n) with period N. The circular convolution is

the same as that of the linear convolution except that the sequences are

periodic. The circular convolution of sequences x(n) — {1,4,2,-1} and

h(n) = {2,3, -1,1} is illustrated in Fig. 14.2. The samples of one period of

the input and output sequences are shown in boldface. The output of one

period is {1,14,14,1}.

290

Convolution and Correlation

Mi)

xli)

h{0 - i)

h{\-

-3

-2

-1

ri-i

h{2-

h(3-

-1

yip)

-1

Fig. 14.2 The circular convolution operation.

TheDFTofar(n) and h(n) are, respectively, X(k) = {6,-l-j"5,0,-l +

j5} and H(k) = {5,3 - j2,-3,3 + j2}. The product of the DFTs is

X(k)H(k) = {30, -13 - jl3,0, -13 + ;13}. The inverse of X(k)H(k) is

y{n) — {1,14,14,1}. Using the transform method, the output is periodic

as the signals are assumed periodic. The superposition sum of the linear

convolution output {2,11,15,1,-1,3,-1} of the two 4-point sequences,

periodically placed at intervals of four samples, produces the periodic out-

put affected by aliasing. The last three values of the linear convolution

are aligned with the first three values and the corresponding terms added.

Note that the fourth output value is correct.

The computation of the linear convolution using the DFT

If we make the period of the input sequences, N, to be at the least P +

Q — 1 (seven for the example) by appending the sequences with zeros,

then aliasing does not occur and the output samples of one period of the

circular convolution correspond to the output of the linear convolution. Let

N = P + Q - 1 and

x'(n)

h'(n)

x(n) for n =

0,1,..

.,P

—

0 forn = P,P +

l,...,N

-1

h(n) for n =

0,1,...,

—

0 forn = Q,Q + l,...,iV-l

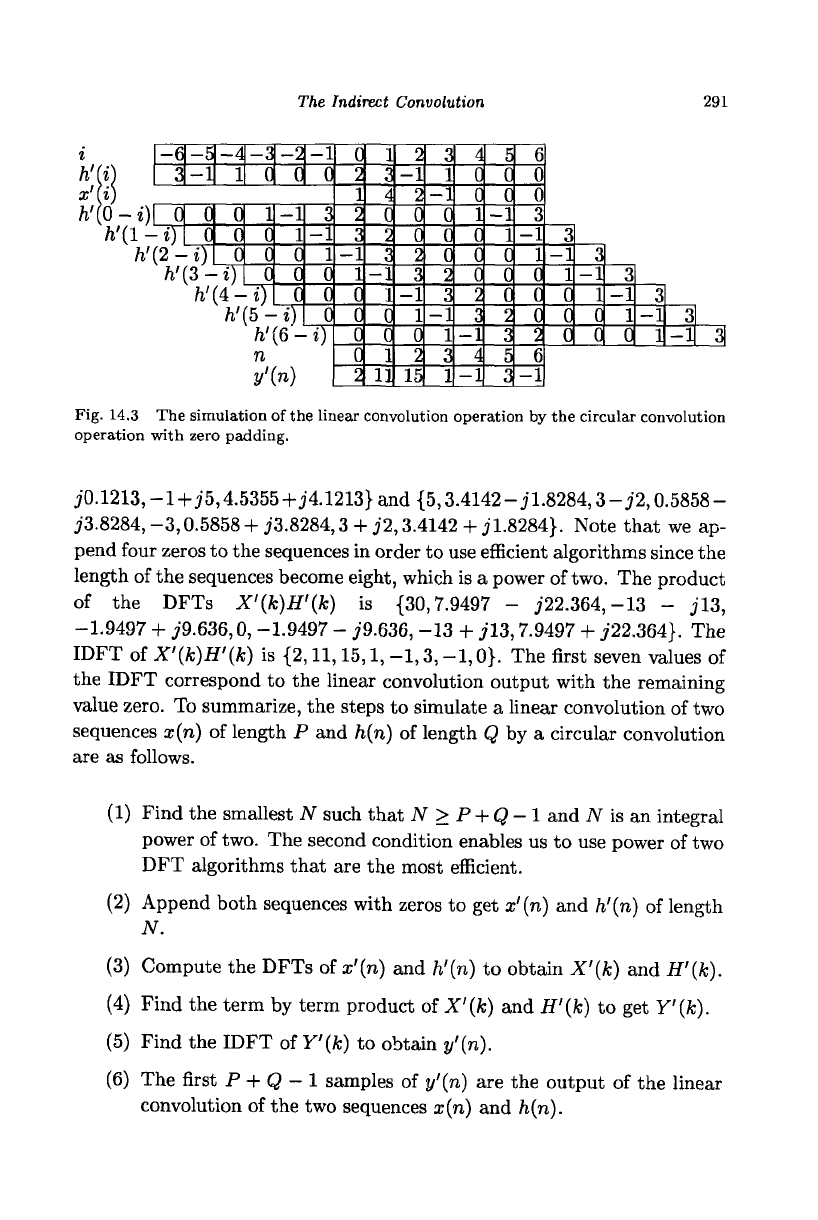
The circular convolution of the sequences of our last example with zero

padding, x'{n) = {1,4,2,-1,0,0,0} and h'(n) = {2,3,-1,1,0,0,0}, is il-

lustrated in Fig. 14.3. The output of one period is

{2,11,15,1,

—1,3,

—1}.

TheDFTofz» = {1,4,2,-1,0,0,0,0}and/i'(n) = {2,3,-1,1,0,0,0,0}

are,

respectively, {6,4.5355-j4.1213,

—1—j'5,

-2.5355-j0.1213,0, -2.5355+

The Indirect Convolution 291

-6

~3|

-5

-1

-4

-3

-2

-1

(2-

•i)

h'(3-

•0

h'(A-

•i)

h'{5-

-1

•i)

h'(6-

-1

•»)

y'(n)

-1

Fig. 14.3 The simulation of the linear convolution operation by the circular convolution

operation with zero padding.

jO.1213,

-1+J5,4.5355 +J4.1213} and {5,3.4142-jl.8284,3- j2,0.5858-

j'3.8284,-3,0.5858+ J3.8284,3 +J2,3.4142+

J1.8284}.

Note that we ap-

pend four zeros to the sequences in order to use efficient algorithms since the

length of the sequences become eight, which is a power of

two.

The product

of the DFTs X'(k)H'(k) is {30,7.9497 - j22.364,-13 - J13,

-1.9497 + j9.636,0, -1.9497 - J9.636, -13 + jl3,7.9497 +

J22.364}.

The

IDFT of X'(k)H'(k) is

{2,11,15,1,

-1,3,

-1,0}.

The first seven values of

the IDFT correspond to the linear convolution output with the remaining

value zero. To summarize, the steps to simulate a linear convolution of two

sequences x(n) of length P and h(n) of length Q by a circular convolution

are as follows.

(1) Find the smallest N such that N > P + Q-l and N is an integral

power of two. The second condition enables us to use power of two

DFT algorithms that are the most efficient.

(2) Append both sequences with zeros to get x'(n) and h'{n) of length

(3) Compute the DFTs of x'(n) and h'{n) to obtain X'(k) and

H'{k).

(4) Find the term by term product of X'{k) and H'(k) to get Y'(fc).

(5) Find the IDFT of Y'(k) to obtain

y'{n).

(6) The first P + Q-l samples of y'(n) are the output of the linear

convolution of the two sequences x(n) and h(n).

292

Convolution and Correlation

Implementation

In practice, signals are real in most applications. To convolve a single real

signal with another real signal, we can use the DFT algorithms described

in Chapters 8 and 9. To convolve two real signals x(ri) and y{n) with a

single real impulse response h(n) (or a single real signal with two impulse

responses), we form a complex signal x'(n) +jy'(n) using the zero padded

signals x'{n) and

y'{n).

Compute the DFT, X'(k) + jY'(k). Compute the

DFT,

H'(k),

of the zero padded impulse response h'(n). Form the term by

term product Z(k) = (X'(k) + jY'(k))H'(k). Compute the IDFT of Z(k).

The real part gives the convolution of x(n) and h(n) and the imaginary

part gives the convolution of y(n) and h(n). This process enables the use

of a DFT algorithm for complex data without the necessity of splitting the

two individual DFTs of x'{n) and

y'(n).

14.3 Overlap-Save Method

In general, the input signal is very long and, therefore, it may not be pos-

sible to manipulate the whole signal or we may not be able to wait too

long for the output. In such cases, the convolution operation is carried

out over sections of the input signal. For example, consider the impulse

response, h(n), of length Q = 4 and the input signal, x(n), of length

P = 14 shown in Fig. 14.4. (For illustrative purposes, we use a short

length of P = 14. However, the input sequence should be very long to

take advantage of this method.) The input signal is extended at the front

by Q

—

1 = 3 zeros. Remember that the circular convolution without

zero padding yields incorrect values at the beginning. We have to choose

a block length. Let us say we choose a block length of 8. Then, the

h(n)

x(n)

~o1

310 0

6101010101010 1

3101010|0 1

y{n) 1141151341441291381401521351131161301391381471481181 0 | 0 [ 0

Fig. 14.4 The overlap-save method of convolution of long sequences.

Overlap-Save Method

293

impulse response is zero padded on the right to make it equal to the

block length and we get {2,1,4,3,0,0,0,0}. The DFT of this, with a

precision of 2 digits, is

1.25,0.07

-jO.85, -0.25 + jO.25,0.43 + jO.15,0.25,

0.43 - jO.15, -0.25 - jO.25,0.07 + jO.85. The DFT values are divided by,

TV = 8, the block length so that we do not need to divide every time an

IDFT is computed. Note that, as the impulse response is fixed, we have to

compute this DFT only once. Also, as the DFT is conjugate-symmetric,

the storage of half of the transform is sufficient.

The input data is divided into overlapping blocks of size 8. There are 4

blocks for the present example. The blocks correspond to the 4 sets of zero

padded impulse response shown. Note that at the end also we zero pad the

input data so that we get an integral number of blocks. With zero padding,

the length of the input data has become 23. We take the first two input

blocks and make a set of 8 complex numbers by putting the first block val-

ues in real parts and second block values in the imaginary parts. For this

example, we get 0+j'l,0+j3,0+j5,7+j9,4+jl,l+j0,3+j2,5+j4. The

DFT of this, with a precision of 2 digits, is 20 + 25,2.54 + jO.88, -9 +

j6,0.78 -

j'2.29,

-6 - j7, -4.54 + J5.12,11 - jl6, -14.78 -

J3.71.

The

pointwise multiplication of this DFT with that of the impulse response

yields, with a precision of 2 digits, 25 + j31.25,0.94 - j'2.10,0.75 - J3.75,

0.67 - jO.86, -1.5 -

jl.75,

-1.19 +

j'2.85,

-6.75 + jl.25,2.08 - J12.89. The

IDFT (remember the division by 8 required by the IDFT operation has al-

ready been done) of this is 20 + jl4,29 + ;29,15 + j'29,14 + j'38,

15 + j40,34 + j52,44 + j35,29 + jl3. The first three values are discarded.

The last five values of the real part appended by the last five values of the

imaginary part are the first ten values of the convolution output, y(n). We

combine two blocks to make a complex signal in order to use an algorithm

for complex data, rather than taking one block and using an algorithm for

real data since the algorithms for complex data are more regular and sim-

pler. In addition, there is no need to split the individual DFTs. We repeat

this procedure until all the input values are processed. If we end up with

one block at the end, then we still use a complex algorithm by assuming a

block with all zeros. An algorithm for real data can be used. This requires

having two algorithms and the work saved will be little if the data length is

very long. Remember that we have to append Q

—

1 zeros to the sequence

x(n) in order to produce all output values. Since we prefer to use algo-

rithms that require the data length to be an integral power of 2, we may

have to append the data further with zeros. Since, the input blocks are