Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications

Подождите немного. Документ загружается.

304

Discrete Cosine Transform

0.3536

0.4619

* -0.1913

0.3536

-0.3536

* -0.

4619

1913

(e)

0.4157

; 0.0975

-0.2778

-0.4904

0.4157

0.0975

-0.2778

-0.4904

(9)

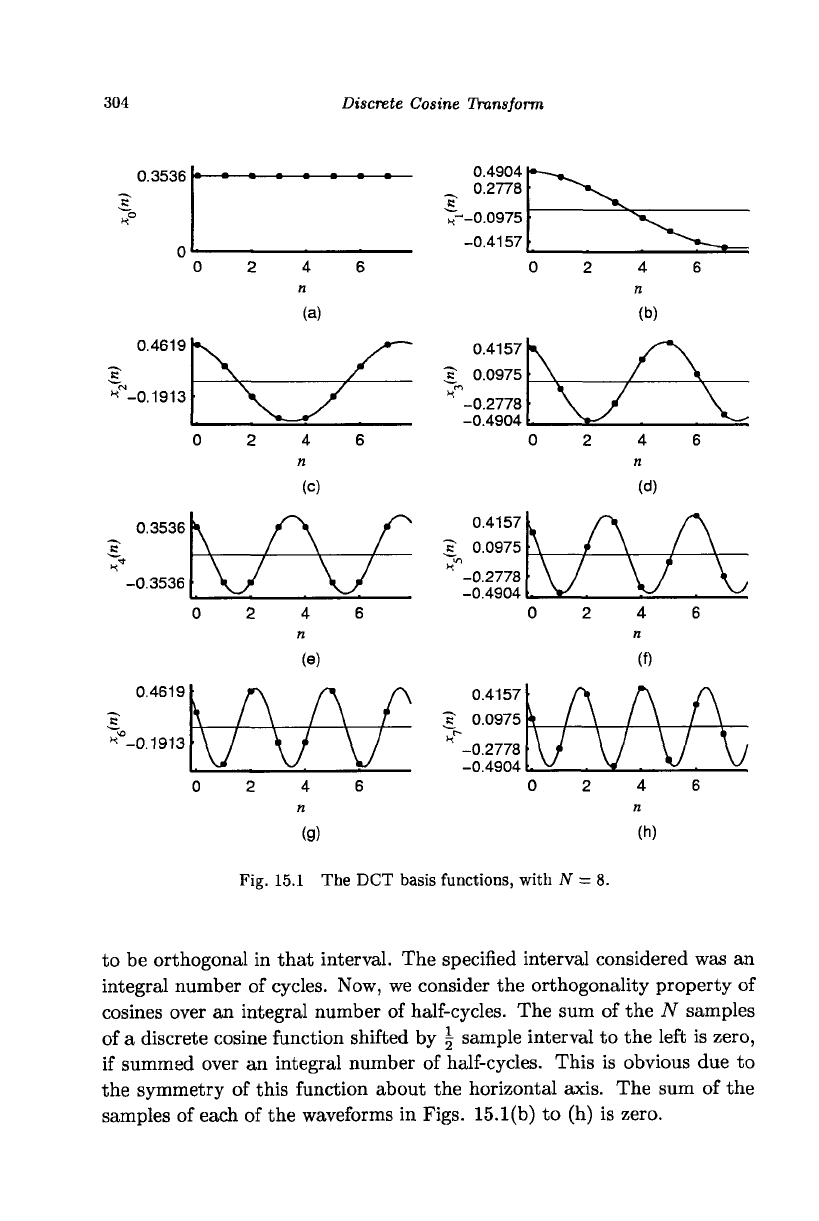
Fig. 15.1 The DCT basis functions, with AT = 8.

(h)

to be orthogonal in that interval. The specified interval considered was an

integral number of cycles. Now, we consider the orthogonality property of

cosines over an integral number of half-cycles. The sum of the N samples

of a discrete cosine function shifted by \ sample interval to the left is zero,

if summed over an integral number of half-cycles. This is obvious due to

the symmetry of this function about the horizontal axis. The sum of the

samples of each of the waveforms in Figs. 15.1(b) to (h) is zero.

The 1-D Discrete Cosine Transform

305

Consider the sum of the product of two cosine waveforms

jv-i f N for I = m = 0

cos ^(2n +

1)1

cos r^r(2n + l)m = < £ for

= m ^ 0

n=o ^ 0 otherwise

This result is clear by rewriting the equation as

N_1

2 ^

(cOS

2^T

(2n + 1)(

' "

m) + C

(2n + 1)(Z + m))

n=0

If I 7^ m, the functions are cosines, as shown in Figs. 15.1(b) to (h), and

their sums over an integral number of half-cycles are zero. If / = m ^ 0,

the sum of the second term evaluates to zero (since it is a cosine) while

the first term is cos (0) and summed over N terms and divided by two

equals y. When I = m = 0, the sum is N. Unlike in the case of the

DFT, we get two nonzero constants. With this orthogonal property, we

can define a transform with basis functions, Xo(n) =

y/ijf)

and Xfc(n) —

^/(jf) cos 2^(2n + l)jfe, n =

0,1,...,

N - 1 and k =

1,2,...,

N - 1, shown

in Fig. 15.1 for N = 8.

15.2 The 1-D Discrete Cosine Transform

The 1-D DCT of a real-valued signal x(n), n =

0,1,...,

—

1 is defined

N-l

{h)

C{k)

)

cos

2^(2" +

k =

0,l,...,N-l

n=0

The 1-D inverse DCT is given by

JV-l

)= ^C^Xctik)cos £-{2n + \)k, n =

0,1,..

.,N - 1

2iV"

fe=o

where

c(fc) =

{$I)

°'

f) for* =

1,2,...,

JV-l

These are the most commonly used definitions. However, it should be noted

that there are other forms also. It is assumed that the data length, N, is

even.

306

Discrete Cosine Transform

Computation of the DCT using the DFT

Splitting the summation in the DCT denning equation into that of the

even-indexed and odd-indexed input samples, we get

Xct(k) = CW{$>(2n)cos^:(2(2n) + l)fc

n=0

+ J^

(

cos

^ (

(

+ !) + !)*}

n=0

By reversing the order of the computation of the products in the second

summation, we get

= C(k){ 53 x(2n) cos ^(2(2n) + l)fc

n=0

JV-1

+ 53 ^(2^ - 2n - 1) cos ^(2(2^ - 2n - 1) + l)Jfe}

Simplifying, we get

„ j JV-i

2?r

= C(*){ 53 *(2n) cos -^ (n + -)fc + 53 x(2iV - 2n - 1) cos -^ (n + -)*}

n=0

Using the rearrangement of the data

xo(n)~S

X{2n)

' » = 0.1.-.f-l

^W-j x(2JV-2n-l),

=f,f+

1,...,7V-1

and combining the two summations, we get

(k)

= C(k) 53 ^o(n) cos — (n + ^)k

n=0

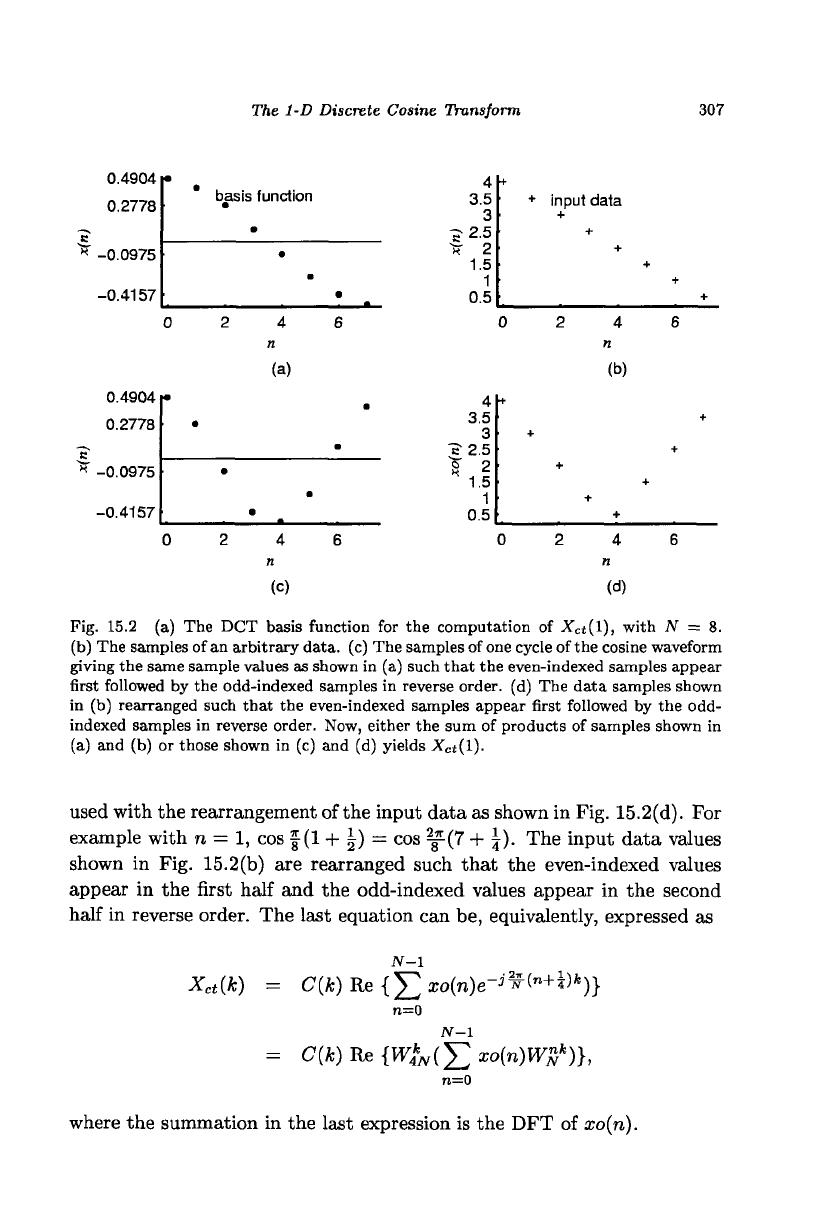
We illustrate the operation of this equation with a specific example. The

computation of X

{(1), with N = 8, involves the sum of products of the

basis function, 0.5cos ^(n + |), and the input data shown, respectively, in

Figs.

15.2(a) and (b). The coefRcient can also be computed by the sum of

product of the functions shown in Figs. 15.2(c) and (d). As the cosine wave

is even-symmetric, a full cycle of the waveform, 0.5cos ^(n + |), can be

The 1-D Discrete Cosine Transform

307

0.4904

0.2778

"* -0.0975

-0.4157

•

0.4904

0.2778

-0.0975

-0.4157

•

bas

•

s function

•

(a)

•

(c)

•

3.5

1?2.5

V 2

1.5

0.5

3.5

•5-2.5

1.5

0.5

input data

(b)

(d)

Fig. 15.2 (a) The DCT basis function for the computation of

t{\),

with N = 8.

(b) The samples of an arbitrary data, (c) The samples of

one

cycle of the cosine waveform

giving the same sample values as shown in (a) such that the even-indexed samples appear

first followed by the odd-indexed samples in reverse order, (d) The data samples shown

in (b) rearranged such that the even-indexed samples appear first followed by the odd-

indexed samples in reverse order. Now, either the sum of products of samples shown in

(a) and (b) or those shown in (c) and (d) yields X

(l).

used with the rearrangement of the input data as shown in Fig. 15.2(d). For

example with n = 1, cos f

+ \) = cos ^(7 + \). The input data values

shown in Fig. 15.2(b) are rearranged such that the even-indexed values

appear in the first half and the odd-indexed values appear in the second

half in reverse order. The last equation can be, equivalently, expressed as

JV-l

(k)

= C{k)Re{Y^xo(n)e~

j¥{n+i)k

)}

n=0

iV-1

= C(k) Re {W?

(J2 xo(n)W%

)},

where the summation in the last expression is the DFT of xo(n).

308 Discrete Cosine Transform

Example 15.1 Compute the DCT,

{k),

of x(n) =

{2,1,0,3}.

Com-

pute x(n) back from Xctik).

Solution

Form the sequence xo(n) =

{2,0,3,1}.

Compute the DFT of xo(n), XO(k) —

{6,

—1

—1 —

j}. The twiddle factors are

Wfe = {1,0.92 - jO.38,0.71 - jO.71,0.38 - j'0.92}

Multiplying XO(k), term by term, by

W*Q

and taking the real parts, we

get {6.0,-0.54,2.83,-1.31}. A more efficient procedure for this step is

as follows. As the DFT is conjugate-symmetric, if XO(k) = a + jb, then

XO(N

—

k) = a

—

jb. The twiddle factors are related in the following way.

If W*

= c + jd, then W\

~ = —d

—

jc. Therefore, the products are

related.

(a+jb)(c + jd) = (ac-bd)+j(ad + bc)

—

jb)(—d

—

jc) =

—

(ad + be)

—

j (ac

—

bd)

The imaginary part of the product

XO(k)

in the first half is the nega-

tive of the value of the real part with index N

—

k. Therefore, multiplication

with the twiddle factors over half the range is sufficient. Now,

X^k)

= C(fc){6.0, -0.54,2.83, -1.31} = {3.0, -0.38,2.0, -0.92}

The inverse: We trace the steps backwards. Multiply X

tik) by constants

for

= 0 and J\ for other values of k to get {1.5,

-0.27,1.41,

-0.65}.

Due to the property mentioned above, the complex signal, W*

XOik), can

be constructed with a scale factor as

{1.5,

-0.27 + jO.65,1.41 -

jl.41,

-0.65 + jO.27}

Now, XOik) can be computed with a scale factor as

^{1.5,

-0.27 + jO.65,1.41 -

jl.41,

-0.65 + jO.27}

= {1.5, -0.50 + jO.50,2, -0.50 - jO.50}

These values have been normalized for DCT. For taking the IDFT the first

value must be multiplied by JV = 4 and other values by y = 2 (Note

that the number of multiplication by constants can be minimized in the

implementation of the algorithm.) to get XOik) = {6, -1 + j,4, -1

—

j}.

Computing the IDFT of XOik), we get xoin) =

{2,0,3,1}.

The first half

The 2-D Discrete Cosine Transform 309

is the even-indexed values of the input data and the second

half,

in reverse

order, are the odd-indexed values. I

The computational complexity of the DCT is that of computing the

DFT of an TV-point real data, in addition to 2N

—

3 real multiplications

and N

—

2 real additions.

15.3 The 2-D Discrete Cosine Transform

The 2-D DCT of a real-valued signal x(ni, n

), n\, n

0,1,...,

—

1 is

defined as

JV-1 JV-1

)

= C{k

)C{k

) ]T 53x(ni,n

)co8^(2ni + l)*i

ni=0 ri2=0

x cos—:(2n

+ l)fe2, h,k

= 0,1, ...,N - 1

where C(fci) and C(k

) are as defined in the last section. The 2-D inverse

DCT is defined as

N-l

x(n

) = Yl Yl C(fci)C(fc2)X

(fci,fc

)cos^r(2ni + l)fci

ki=0k

x cos—(2n

+ l)k

, ni,n

0,1,...,

N - 1

The transform is separable and can be computed by the row-column method.

For example, the 2-D DCT can be written as

N-l JV-1

Xct(k

) = C(fc

) £{£(*!) ^x(n

)cos^(2n

+ l)A;

}

ri2=o m=o

xcos—(2n

+ l)A;

Therefore, the algorithm for computing the 2-D DCT is to compute the 1-D

DCT of each row of the image followed by the 1-D DCT of each column of

the resulting data and vice versa.

310 Discrete Cosine Transform

Example 15.2 Compute the 2-D DCT of the following matrix of data.

The origin is at upper left-hand corner.

2.50 •

1.04

1.50

1.19 .

Computing 1-D DCT of the rows, we get

(ki,

fo) as

1.98 "

1.07

1.60

2.95 .

The original image can be obtained by computing 1-D inverse DCT of each

row of the transform matrix followed by 1-D inverse DCT of each column

of the resulting matrix and vice versa. I

15.4 Summary

• In this chapter, algorithms for the computation of the 1-D and 2-D

DCT were described. It was pointed out that the DCT is essentially

the DFT of an even-extended real signal. Reordering of the input

data makes the problem of computing the DCT into a problem of

computing the DFT of a real signal with a few additional opera-

tions.

This approach provides regular, simple, and very efficient

13 11

4 0 4 1

3 2 10

2 14 3

Solution

Computing 1-D DCT of the columns, we get

5.00

0.38

2.00

0.92

3.00

0.77

1.00

1.85

5.00

-1.15

0.00

-2.77

->•

7.75 1.09 -0.25

-0.90 0.95 -0.52

0.25 -2.02 -0.75

-1.52 1.43 -0.60

Exercises

311

DCT algorithms for practical hardware and software implementa-

tions.

References

(1) Guillemin, E. A. (1952) The Mathematics of Circuit Analysis, John

Wiley, New York.

(2) Gonzalez, R. C. and Woods, P. (1987) Digital Image Processing,

Addison Wesley, Reading, Mass.

(3) Jain, A. K. (1989) Fundamentals of Digital Image Processing, Prentice-

Hall, New Jersey.

Exercises

15.1 Compute the DCT,

(k),

of x(n) = {3,4,5,6} using the DFT.

Compute x(n) back from

t(k).

* 15.2 Compute the 2-D DCT of the following matrix of data using the

DFT. The origin is at upper left-hand corner.

-¥

14 2 3"

5 6 4 1

2 5 13

3 0 4 1

Chapter 16

Discrete Walsh-Hadamard Transform

In computing the DFT, we find the representation of a signal in terms of a

set of

sinusoids.

In the case of discrete Walsh-Hadamard transforms, we rep-

resent a signal in terms of a set of orthogonal rectangular waveforms. These

transforms represent signals with discontinuities more efficiently and they

are useful in image processing tasks. These transforms can be computed

using algorithms those are very similar to the DFT algorithms. One of the

advantages of this type of transforms is that they do not require multiplica-

tion operations in their computation and, hence, require less computational

effort than the DFT. The study of the DFT and these transforms provides

a contrast in representing a signal by two sets of orthogonal functions, si-

nusoids and rectangular waveforms.

In Sec.

16.1,

the discrete Walsh transform (DWT) and the PM DWT al-

gorithm are presented. In Sec. 16.2, the naturally ordered discrete Hadamard

transform (NDHT) and the PM NDHT algorithm are described. In Sec. 16.3,

the sequency ordered discrete Hadamard transform (SDHT) and the PM

SDHT algorithm are developed.

16.1 The Discrete Walsh Transform

In this chapter, it is assumed that N, the number of samples of the data,

is an integral power of two and M = log

N. The DWT of a data sequence

{x(n),

n =

0,1,...,

N - 1} is defined as

N-l

M-l

*„(*) = £

x(n)

IJ (-ir*"-*-«, ft =

0,1,...,

AT-1,

n=0 t=0

313