Sundararaja D. The Discrete Fourier Transform. Theory, Algorithms and Applications

Подождите немного. Документ загружается.

334

The Complex Numbers

•-1+/J

,-2+yO

.-2-yi |

2+/2

,o+y

0+yO

2-/2

-2-1 0 1 2

Fig. A.l The complex plane with some complex numbers.

than using vector algebra or vector diagrams. When the second of the pair

of ordered numbers is zero, it is equivalent to a real number. The set of

real numbers is a subset of the complex numbers.

Rectangular Form

Figure A.l shows some complex numbers in the complex plane. Remember

that the negative symbol '-' is used to represent n radians or 180 degrees

(the angle formed by the positive and the negative real axis). Similarly,

the symbol j is used to indicate an angle of \ radians or 90 degrees. The

rectangular form of a complex number is given by x + jy where x and y are

real numbers and j — y/—l since jj = j

—1,

a rotation of 180 degrees.

The number x is called the real part and y is called the imaginary part of

the complex number and j is called the imaginary unit. If the real part of

a complex number is zero (the number 0 + jl), it is called a pure imaginary

number (a number on the imaginary axis). If the imaginary part is zero

(the number -2+jO), it is called a pure real number (a number on the real

axis).

Let Zi = xi + jyi and z

— x

+ J2/2- The complex numbers z\ and z

are equal if and only if x\

—

and y\ =yi-

Addition

= z\ + z

, where z

= (xi + x

) + j(yi +1/2)

Subtraction

zi - z

, where z

= (xi - x

) + j(yi - 2/2)

Polar Form

335

Multiplication

23 = ziz

, where z

= (xix

- 2/12/2) + j(xiy

+ x

yi)

Conjugation

The conjugate of a complex number z = x+jy, denoted by z*, is defined

asz* = x—jy, that is the imaginary part is negated. The complex conjugate

pair 2 + j2 and 2

—

j2 is shown in Fig. A.l. z + z* = 2x, z

—

j2y, and

zz* = x

+ y

. The complex conjugate of an expression is equivalent to the

expression with every complex quantity conjugated.

(Zl

=Z*+Z*,

(Zx - Z

)* = Z* - Z*, (Z!Z

)* =

Z*Z

Division

_ zi _ ziz* _ {x

+ 2/12/2) + j(x

yi -

xi)

3 — — — T — o~, 9

Z^ X\ + J/2

Polar Form

A point in the complex plane can also be represented by its distance from

the origin, called the magnitude (the magnitude is always a positive num-

ber),

and the angle, called the argument, formed by the line joining the

point and the origin, and the positive real axis. The magnitude A and the

argument 8 can be obtained from the rectangular form x + jy as

A = +x/(a;

+ 2/

), 9 = tan""

The polar form is written as Aid. As ALQ = AL(Q + 2kir), where k is an

integer, the value of the argument 6 such that — it < 6 <

is called its prin-

cipal value. From polar representation, the components of the rectangular

form can be derived as x = ^4cos0 and y = AsinO. Using Euler's identity,

we get

= Acos0 + jAsinO

The expression on the left is called the exponential form of the complex

number. The multiplication and division operations are relatively easier to

carry out in the polar or exponential form.

= z

= A

e^A

* =

336

The Complex Numbers

e^ A

Powers and Roots

Let z = re

. Then, z

(re

)

= r

, where N > 1 is an integer.

Since 2kir can be added to the argument of a complex number, where k is

an integer, without changing its value and replacing N by jj, we get for

z^O

X 1

„•

2fcir + 9

•=. fit Ql N .

Expanding the equation, we get the N distinct roots as

y~z=

^(cos^±f+jsin^±f), fc = 0,l,...,JV-l (A.l)

where %/f is the real positive root. For example, letting r

—

1, 6 =

TT,

and

N = 2, with

= 0, we get

(cos-+jsin-) =0 + jl

and, with k = 1, we get

. 37T . . 37T.

(cos y+jsiny)=0-jl

The square of both the roots equals e*-

^ = —

The Roots of Unity

Of particular interest to DFT are the N roots of unity, that is the solutions

of the equation x

—

1 = 0. In mathematical literature, the computation

of the DFT is referred to as the evaluation of a polynomial of degree N

—

at N values of the roots of unity. The usual representation of a polynomial

is with its coefficients. For example, the representation of the polynomial

2 + 3x with its values at the two roots of unity

(1,

-1) is (5, -1), obtained

by evaluating the polynomial at 1 and

-1.

In electrical engineering litera-

ture,

the computation of the DFT is referred to as the evaluation of the

^-transform at JV equally spaced points on the unit circle.

The Complex Exponential, and Cosine and Sine Functions 337

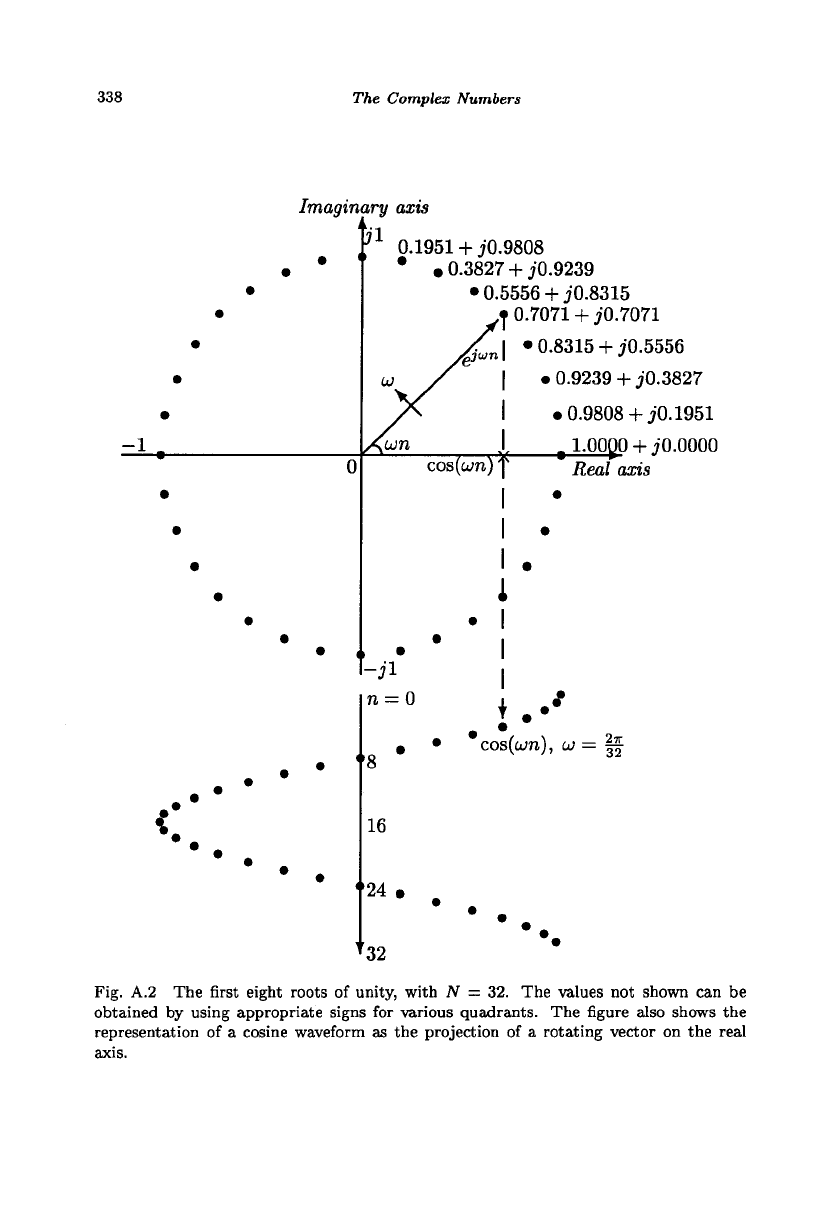
By letting r = 1 and 6 = 0 in Eq. (A.l), we get N complex numbers,

called the iVth roots of unity, as

VI = (cos ^+ j sin ^),

= 0,1,...,JV-1

With N = 2, the roots are 1 + jO and -1 + jO. With N = 3, the roots

are 1 + jO, -| +

j^,

and -\ -

j^.

With JV = 4, the roots are 1 + jO,

0 + jl,

—1

+ jO, and 0 - jl. The first eight roots, with N = 32, are shown

in Fig. A.2. By using appropriate signs, the other roots can be obtained.

These are the values of

= wi

= o,i,...,3i

The Complex Exponential, and Cosine and Sine Functions

Let us express the complex exponential in the series form. The series rep-

resentation is similar to that of a real exponential.

6 1

+ W";+ 2! 3! 4! ' (r)!

The exponent can be any complex number, but our interest is primarily in

the complex exponential with a pure imaginary exponent. One half of the

numbers in the series are pure real and the other half pure imaginary. If

we group the two sets, we get

•»><i-£

S--)

i(#-£

£-->

The two expressions in parenthesis on the right-hand side are series ex-

pansions for cosine and sine functions, respectively. Therefore, we get the

Euler's identity

= cos 6 + j sin

The Representation of a Real Sinusoid

Figure A.2 shows thirty-two equidistant points of a circle of radius one and

center at origin. By definition, the projection of any point on the real axis

is cos#, where 8 is the angle formed by the line from the origin to the point

and the positive real axis. The line between a point on the circle and the

338

The Complex Numbers

Imaginary axis

0.1951+

J0.9808

* •

0.3827

j0.9239

•

0.5556+

J0.8315

0.7071

j'0.7071

]un

\ •

0.8315

J0.5556

| •

0.9239

jO.3827

cos

»•

•

0.9808

j0.1951

J- .i-oopo

JO.OOOO

Real axis

•

• I

i.-'

cos(a;n),

= ||

-J'l

n = 0

8 *

24.

*32

Fig. A.2 The first eight roots of unity, with N = 32. The values not shown can be

obtained by using appropriate signs for various quadrants. The figure also shows the

representation of a cosine waveform as the projection of a rotating vector on the real

axis.

The Representation of a Real Sinusoid

339

Imaginary axis

';'0.5

0.5 ^

S(UJn)

2 ' 2

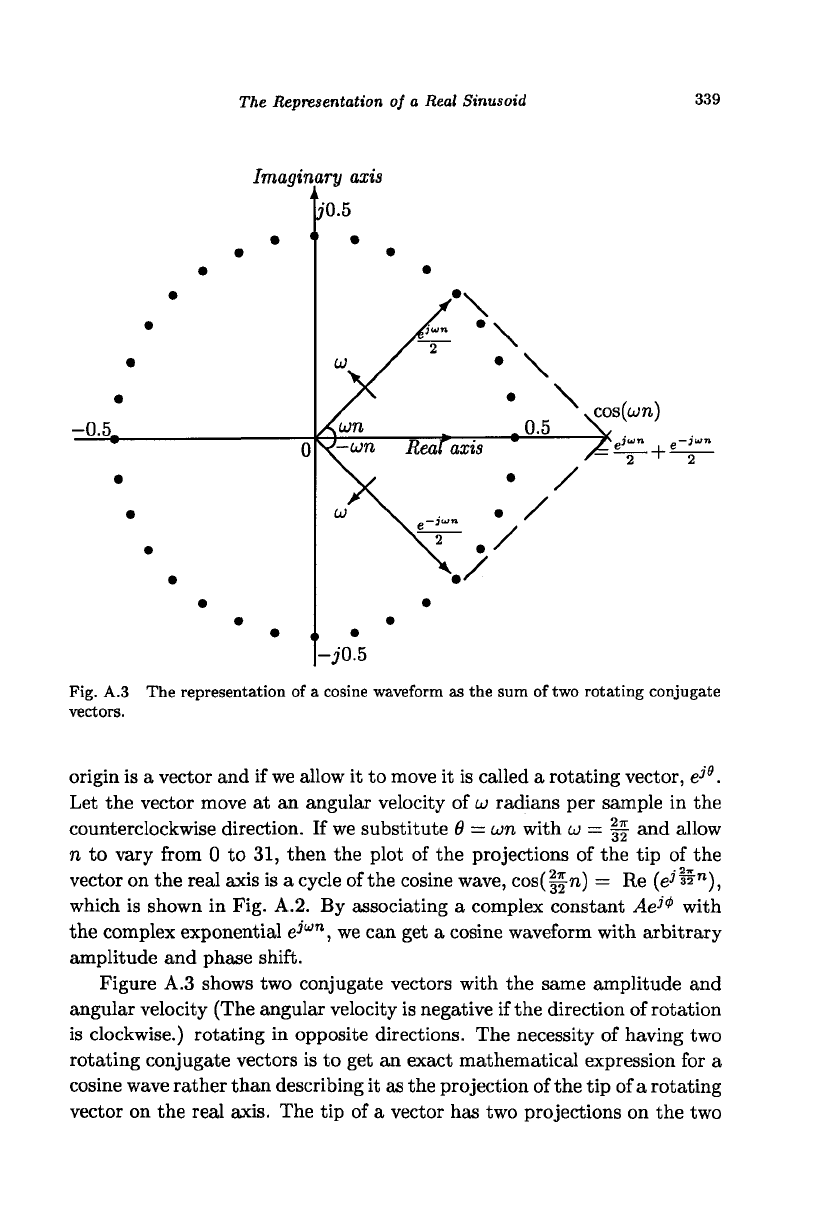
Fig. A.3 The representation of a cosine waveform as the sum of two rotating conjugate

vectors.

origin is a vector and if we allow it to move it is called a rotating vector, e

Let the vector move at an angular velocity of

radians per sample in the

counterclockwise direction. If we substitute 6

—

wn with u = |f and allow

n to vary from 0 to 31, then the plot of the projections of the tip of the

vector on the real axis is a cycle of the cosine wave, cos(|f-n) = Re [e?"&"),

which is shown in Fig. A.2. By associating a complex constant Ae^ with

the complex exponential e

Jwn

, we can get a cosine waveform with arbitrary

amplitude and phase shift.

Figure A.3 shows two conjugate vectors with the same amplitude and

angular velocity (The angular velocity is negative if the direction of rotation

is clockwise.) rotating in opposite directions. The necessity of having two

rotating conjugate vectors is to get an exact mathematical expression for a

cosine wave rather than describing it as the projection of the tip of a rotating

vector on the real axis. The tip of a vector has two projections on the two

340

The Complex Numbers

axes.

By having two conjugate vectors rotating in opposite directions, we

can cancel either of the projections and generate a sinusoid in terms of

phase-shifted cosine or sine waveform. Although it is an arbitrary choice,

we use the phase-shifted cosine to represent a sinusoid in this book.

Appendix B

The Measure of Computational

Complexity

An algorithm is a systematic procedure to solve a problem. As there can

be many algorithms to solve a problem, a measure is required to evaluate

the relative merits of the algorithms. While the ultimate measure is the

execution time of the algorithms on the same computer, however, we need

a measure that is independent of the computer used although it may be

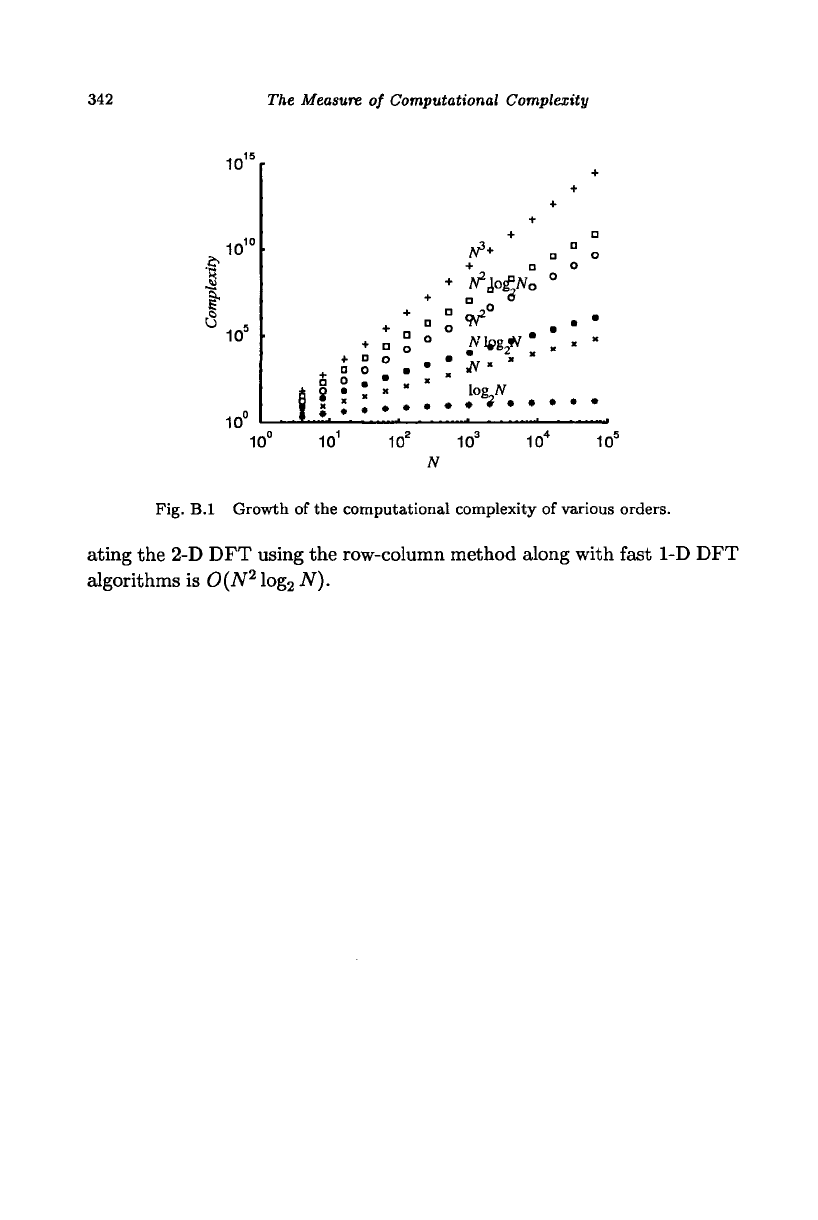
less precise. Such a measure is given by a function that indicates the rate

of increase in the number of major operations, such as multiplications,

additions, or comparisons, as the number of elements in the input data is

increased. For example, if the number of operations required to execute an

algorithm is proportional to JV, the data size, then it is referred to have a

computational complexity of 0(N). The constant of proportionality and

any terms of a lower order are ignored. The growth of the computational

complexity of various orders is shown in Fig. B.l. For a large JV, the

execution time will be proportional to the computational complexity. For

very small JV, due to reduced overhead operations, an algorithm with an

higher order of complexity could run faster. When comparing algorithms

of the same order of complexity, we have to consider several factors such

as run-time, overhead operations, memory required, regularity, simplicity,

stability, and numerical accuracy to find out which algorithm is practically

better.

The computational complexity of directly evaluating the 1-D DFT is

0(JV

) and that of using fast 1-D DFT algorithms is 0(JVlog

JV). The

computational complexity of directly evaluating the 2-D DFT is 0(JV

The computational complexity of directly evaluating the 2-D DFT using

the row-column method is

0(N

The computational complexity of evalu-

341

342

The Measure

Computational Complexity

Complex

-m"

•

" o

• o

„ °

NlBSf

, " "

• * X

log^V

10"

10' 10'

10'

10°

Fig.

B.l

Growth

the computational complexity

various orders.

ating the 2-D DFT using the row-column method along with fast 1-D DFT

algorithms is 0(N

log

N).

Appendix C

The Bit-Reversal Algorithm

The Number System

A number consists of i digits in sequence, each digit taking any of r possible

values, written as ni-i,rii-2,

• •

.,rii,no- The symbol r represents the radix

or base of the number system. In the familiar decimal number system

r = 10, indicating that there are 10 distinct digits used in that number

system, namely {0,1,2,3,4,5,6,7,8,9}. The decimal number 253 is equal

to 2 x 10

+ 5 x 10

+ 3 x 10°. If we use only two digits {0,1} (r = 2),

then the number system is called radix-2 or binary number system. A digit

in the binary number system is called a bit (fiinary digit). The rightmost

bit, no, is called the least significant bit (lsb) and the leftmost bit, rij_i, is

called the most significant bit (msb). The binary number 11001 is equal to

1 x 2

+ 1 x 2

+ 0 x 2

+ 1 x 2° = 25 in decimal.

Conversion of a Decimal Number into a Binary Number

One way of converting a decimal number into the corresponding binary

number is to find the bits from msb to lsb. Remember that each bit has a

weight attached to it depending on its position. The weight attached to bit

is 2° = 1 and, in general, the weight of a bit n» is 2*. Given a decimal

number, find the largest weight that is equal to or just less than the decimal

number. For example, the largest weight that is equal to or just less than

25 is 16. Therefore, we fix m = 1 and subtract 16 from 25 to get 9. We

repeat the process again with 9 and continue until the number becomes a

0 or 1. Every weight must be tested in decreasing order. Note that if the

343