Сударикова Е.В. Неразрушающий контроль в производстве. Часть 2
Подождите немного. Документ загружается.

81
Элементарной операцией здесь можно считать процесс входного
контроля одной партии труб (объем партии – константа).
Любую систему, в которой поток требований встречает ограничен
ные средства их удовлетворения, можно рассматривать как систему
массового обслуживания (СМО). В частности, если моменты поступ
ления требований или продолжительность их обслуживания не рег
ламентируются, то при пользовании системой возникают конфлик
ты и образуется очередь. Длина этой очереди зависит от двух харак
теристик потока требований: вопервых, она зависит от интенсив
ности поступления требований и, вовторых, от статистических
флуктуаций этой интенсивности. Конечно, если интенсивность по
ступления требований превышает пропускную способность системы,
то система не справляется с потоком этих требований, и начитает
расти очередь неограниченной длины. Однако, если даже интенсив
ность поступления требований меньше пропускной способности сис
темы, очередь может образоваться изза статистических флуктуаций
и внезапного накопления требований (которое может случиться).
Влияние таких колебаний в большой степени увеличивается, если
средняя нагрузка приближается к пропускной способности системы
(но необязательно достигает ее). Простота таких СМО обманчива, и
при их исследованиях приходится прибегать к глубоким аналити
ческим выкладкам. К счастью, исследование СМО может быть вы
полнено на основе одного хорошо известного фундаментального за
кона науки. Это – закон сохранения потока, состоящий в том, что
интенсивность роста числа требований в системе определяется раз
ностью интенсивностей входящего и исходящего потоков. Этот факт
позволяет сравнительно легко составить основную систему уравне
ний для СМО достаточно сложной структуры.
4.2. Потоки событий. Марковские случайные процессы
4.2.1. Понятие потока событий.
Простейший поток событий
Потоком событий называется последовательность однородных
событий, появляющихся одно за другим в случайные моменты вре
мени.
Примеры: поток вызовов на телефонной станции; поток забитых
шайб при игре в хоккей; поток сбоев ЭВМ; поток продукции на про
ведение НК и т. п.
Поток событий называется простейшим, если он стационарен,
ординарен и не имеет последействия.

82
Поток событий называется ординарным, если вероятность попа
дания на элементарный интервал времени Δt двух или более событий
пренебрежимо мала по сравнению с вероятностью попадания одного
события. Практически ординарность потока означает, что события в
нем появляются «поодиночке», а не группами по два, по три и т. д.
(точное совпадение моментов появления двух событий теоретически
возможно, но имеет нулевую вероятность).
Поток событий называется потоком без последействий, если
число событий, попадающих на любой интервал времени τ, не зави
сит от того, сколько событий попало на любой другой непересекаю
щийся с ним интервал. Практически отсутствие последействий в по
токе означает, что события, образующие поток, появляются в те или
иные моменты времени независимо друг от друга.
Интервал времени T между двумя соседними событиями простей
шего потока имеет показательное распределение
()
t
ft e
−λ
=λ
(при t > 0), (4.1)
где
[]
1
MT
λ=
– величина, обратная среднему значению интервала T.
Интенсивностью
λλ
λλ
λ потока событий называется среднее число
(математическое ожидание числа) событий, приходящееся на едини
цу времени. Для стационарного потока λ = const; для нестационарно
го потока интенсивность в общем случае зависит от времени: λ =λ (t).
4.2.2. Частные случаи потоков событий
1. Ординарный поток событий без последействия называется пу
ассоновским. Простейший поток есть частный случай пуассоновс
кого (а именно стационарный пуассоновский поток).
2. Одинарный поток событий называется потоком Пальма (или
рекуррентным потоком, или потоком с ограниченным последействи
ем), если интервалы времени T
1
, T
2
, … между последовательными
событиями представляют собой независимые, одинаково распреде
ленные случайные величины. В связи с одинаковостью распределе
ний T
1
, T
2
, … поток Пальма всегда стационарен.
Простейший поток является частным случаем потока Пальма; в
нем интервалы между событиями распределены по показательному
закону (4.1), где λ – интенсивность потока.
3. Потоком Эрланга k порядка называется поток событий, полу
чающийся «прореживанием» простейшего потока, когда сохраняет
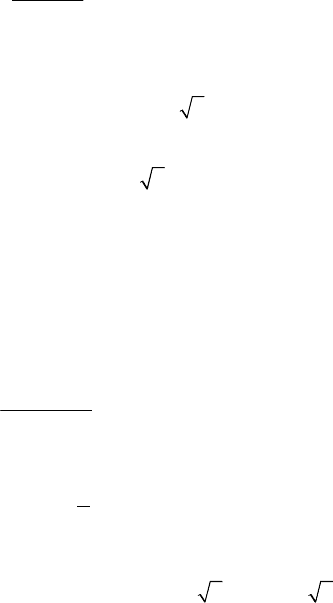
83
ся каждая kя точка (событие) в потоке, а все промежуточные выбра
сываются.
Интервал времени между двумя соседними событиями в потоке
Эрланга kго порядка представляет собой сумму k независимых слу
чайных величин T
1
, T
2
, …, T
k
, имеющих показательное распределе
ние с параметром λ:
1
.
k
i
i
TT
=
=
∑
(4.2)
Закон распределения случайной величины T называется законом
Эрланга kго порядка и имеет плотность
1
()
()
(1)!
k
t
k
t
ft e
k
−
−λ
λλ
=
−
(при t > 0).
Математическое ожидание, дисперсия и среднее квадратическое
отклонение случайной величины T (4.2) соответственно равны:
2
/; / ; /.
tt t
mk Dk k=λ =λσ= λ
Коэффициент вариации случайной величины (4.2) равен
/1/;
ttt
vm k=σ =
v
t
→ 0 при k → ∞, т. е. при увеличении порядка потока Эрланга «сте
пень случайности» интервала между событиями стремится к нулю.
Если одновременно с «прореживанием» простейшего потока из
менять масштаб по оси 0t (делением на k), получится нормирован
ный поток Эрланга kго порядка, интенсивность которого не зависит
от k. Интервал времени
T
1
между соседними событиями в нормиро
ванном потоке Эрланга kго порядка имеет плотность
1
()
()
(1)!
k
kt
k
kkt
ft e
k
−
−λ
λλ
=
−
1
(при t>0).
Числовые характеристики случайной величины
1
1
k
i
i
TT
k
=
=
∑
1
равны:
2
1/ ; 1/ ; 1/( ); 1/ .
tt
MT DT k k v k
⎡⎤ ⎡⎤
=λ = λσ= λ =
⎣⎦ ⎣⎦
11
1
При увеличении k нормированный поток Эрланга неограниченно
приближается к регулярному потоку с постоянным интервалом
l = 1/λ между событиями.
84
4.2.3. Понятие марковского случайного процесса
Случайный процесс, протекающий в какойлибо физической сис
теме, называется марковским (или процессом без последействий),
если он обладает следующим свойством: для любого момента време%
ни t
0
(рис. 4.1) вероятность любого состояния системы в будущем
Рис. 4.1. К определению марковского случайного процесса
0
tt
0
tt
0
t
t
(?
@
>H;>5)
(1C4CI55)
(=0AB>OI55)
(при t > t
0
) зависит только от ее состояния в настоящем (при t = t
0
)
и не зависит от того, когда и каким образом система пришла в это
состояние (иначе: при фиксированном настоящем будущее не зави
сит о предыстории процесса – от прошлого).
4.2.4. Граф состояний. Схемы гибели и размножения.
Размеченный граф состояний
Марковские процессы с дискретными состояниями s
1
, s
2
, …, s
n
удоб
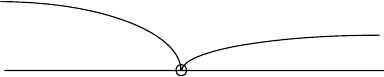
но иллюстрировать с помощью графа состояний (рис. 4.2), где пря
моугольниками (или кружками) обозначены состояния s
1
, s
2
, … сис
темы S, а стрелками – возможные переходы из состояния в состояние
(на графе отмечаются только непосредственные переходы, а не пере
ходы через другие состояния). Иногда на графе состояний отмечают
не только возможные переходы из состояния в состояние, но и воз
можные задержки в прежнем состоянии; это изображается стрелкой
(«петлей»), направленной из данного состояния в него же (рис. 4.3),
но можно обходиться и без этого. Число состояний системы может
быть как конечным, так и бесконечным (но счетным).
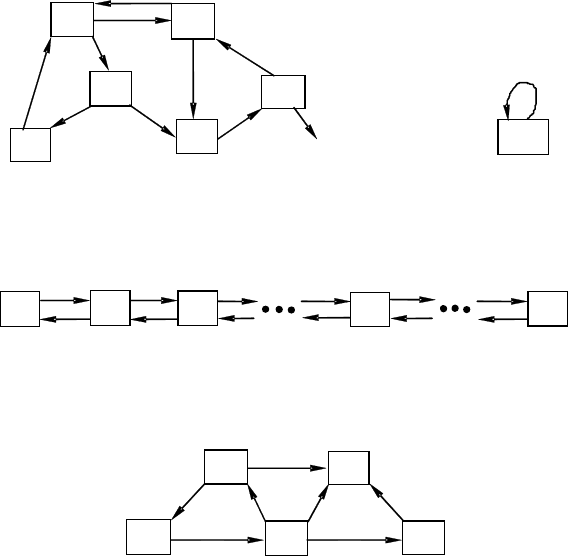
На практике часто приходится встречаться с системами, граф со
стояний которых имеет вид, показанный на рис. 4.4 (все состояния
можно вытянуть в цепь, причем каждое из них связано прямой и
обратной связью с двумя соседними, кроме двух крайних, каждое из
которых связано только с одним соседним). Схема, показанная на
рис. 4.4, называется схемой гибели и размножения. Это название
заимствовано из биологических задач, где состояние популяции s
k
85
означает наличие в ней k единиц. Переход вправо связан с «размно
жением» единиц, а влево – с их «гибелью». «Интенсивности размно
жения» (λ
0
, λ
1
, …, λ
n–1
) проставлены у стрелок, ведущих слева напра
во, «интенсивности гибели» (μ
1
, μ
2
, …, μ
n–1
) – у стрелок, ведущих
справа налево; каждая из них отмечена индексом того состояния, из
которого исходит соответствующая стрелка.
Для СМО «интенсивности размножения» (λ
0
, λ
1
, …, λ
n–1
) имеют
смысл, например, интенсивности поступления заявок; «интенсив
ности гибели» (μ
1
, μ
2
, …, μ
n–1
) – смысл интенсивности потока обслу
живаний.
Рассматривая марковские случайные процессы с дискретными со
стояниями и непрерывным временем, очень удобно пользоваться раз%
меченным графом состояний, на котором против каждой стрелки,
ведущей из состояния s
i
в s
j
, поставлена интенсивность λ
ij
потока
событий, переводящего систему по данной стрелке (рис. 4.5).
Рис. 4.2. Граф состояний
s
1
s
2
s
3
s
4
s
5
s
6
s
i
Рис. 4.3. Задержка
в прежнем
состоянии
Рис. 4.4. Схема гибели и размножения
s
1
s
0
s
2
s
k
s
n
0
1
2
1k
k
1
n
1
2
3
k
1
k
n
s
1
s
2
s
3
s
4
s
5
12
14
54
35
23
31
34
Рис. 4.5. Размеченный граф состояний

86
4.2.5. Уравнения Колмогорова
Пусть в момент времени t система S находится в состоянии s
i
. Ве
роятность этого есть p
i
(t).
Вероятность того, что система, находящаяся в состоянии s
i
, за
элементарный промежуток времени (t, t + dt) перейдет в состояние s
j
,
есть вероятность того, что за это время dt появится хотя бы одно
событие потока, переводящего S из s
i
в s
j
. С точностью до бесконечно
малых высших порядков эта вероятность равна λ
ij
dt, где λ
ij
– интен
сивность соответствующих потоков событий (как только происхо
дит первое событие в потоке с интенсивностью λ
ij
, система из состоя
ния s
i
скачком переходит в s
j
).
Потоком вероятности перехода из состояния s
i
в s
j
называется
величина λ
ij
p
i
(t), причем интенсивность λ
ij
здесь может быть как за
висящей, так и независящей от времени.
Рассмотрим случай, когда система S имеет конечное число состоя
ний s
1
, s
2
, …, s
n
. Для описания случайного процесса, протекающего в
этой системе, применяются вероятности состояний
12
( ), ( ), , ( ),
n
p
tpt pt1
(4.3)
где p
i
(t) – вероятность того, что система S в момент t находится в
состоянии s
i
:
{
}
() () .
ii
p
tPSts==
(4.4)
Очевидно, для любого t
1
() 1.
n
i
i
pt
=
=
∑
(4.5)
Для нахождения вероятностей (4.3) нужно решить систему диф
ференциальных уравнений (уравнений Колмогорова), имеющих вид
d
d
11
()
() () ( 1,2, , )
nn
i
ij j i ij
jj
pt
p
tpt i n
t
==
=λ − λ =
∑∑
1
или, опуская аргумент t у переменных p
i
,
d
d
11
(1,2,,).
nn
i
ij j i ij
jj
p
p
pi n
t
==
=λ − λ =
∑∑
1
(4.6)
Отметим, что интенсивности λ
ij
могут зависеть от времени t (аргу
мент t для краткости написания опущен).
Уравнения (4.6) удобно составлять, пользуясь размеченным гра
фом состояний системы и следующим мнемоническим правилом: про%
87
изводная вероятности каждого состояния равна сумме всех пото%
ков вероятности, идущих из других состояний в данное, минус сум%
ма всех потоков вероятности, идущих из данного состояния в дру%
гие. Например, для системы S, размеченный граф состояний которой
дан на рис. 4.5, система уравнений Колмогорова имеет вид
dd
dd
dd
dd
dd
131312141
2121232
3 23 2 31 34 35 3
4141343545
5351545
/();
/;
/( );
/;
/.
pt p p
pt p p
pt p p
pt p p p
pt p p
=λ − λ +λ
⎫
⎪
=λ −λ
⎪
⎪
=λ − λ +λ +λ
⎬
⎪
=λ +λ +λ
⎪
⎪
=λ −λ
⎭
(4.7)
Поскольку для любого t выполняется условие (4.5), можно лю
бую из вероятностей (4.3) выразить через остальные и таким образом
уменьшить число уравнений на одно.
Чтобы решить систему дифференциальных уравнений (4.6) для
вероятностей состояний p
1
(t), p
2
(t), …, p
n
(t), нужно задать начальное
распределение вероятностей
12
(0), (0), , (0), , (0),
in
pp p p11
(4.8)
сумма которых равна единице:
1
(0) 1.
n
i
i
p
=
=
∑
Если, в частности, в начальный момент t = 0 состояние системы S
в точности известно, например, S(0) = s
i
, то p
i
(0) = 1, а остальные
вероятности (4.8) равны нулю.
4.2.6. Финальная вероятность состояний.
Эргодические системы.
Существенные и несущественные состояния
В общем случае вероятности kх состояний s
k
системы S являются
функциями времени: p
k
(t). Во многих случаях, когда процесс, проте
кающий в системе, длится достаточно долго, возникает вопрос о пре%
дельном поведении вероятностей p
k
(t) при t → ∞. Если все потоки со
бытий, переводящие систему из состояние в состояние, являются про
стейшими (т. е. стационарными пуассоновскими с постоянными ин
тенсивностями λ
ij
перехода из состояния s
i
в s
j
), в некоторых случаях
существуют финальные (или предельные) вероятности состояний.
88
Финальная вероятность состояний
()
lim ( ) 1, ,
t
kk
p
pt k n
→∞
==1
не зависит от того, в каком состоянии система S находилась в на
чальный момент. Это означает, что с течением времени в системе S
устанавливается предельный стационарный режим, в ходе которого
она переходит из состояния в состояние, но вероятности состояний
уже не меняются.
В этом предельном режиме каждая финальная вероятность может
быть истолкована как среднее относительное время пребывания
системы в данном состоянии.
Система, для которой существуют финальные состояния, назы
вается эргодической и соответствующий случайный процесс – эрго
дическим.
Для существования финальных вероятностей состояний одного
условия λ
ij
= const недостаточно, требуется выполнение еще некото
рых условий, проверить которые можно по графу состояний, выде
лив на нем «существенные» и «несущественные» состояния. Состоя
ние s
i
называется существенным, если нет другого состояния s
j
та
кого, что, перейдя однажды какимто способом из s
i
в s
j
, система уже
не может вернуться в s
i
. Все состояния, не обладающие таким свой
ством, называется несущественными.
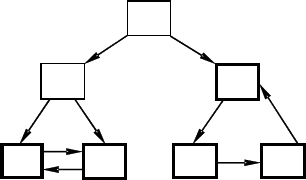
Например, для системы S, граф которой дан на рис. 4.6, состоя
ния s
1
, s
2
несущественны (из s
1
можно уйти, например, в s
2
и не вер
нуться, а из s
2
в s
4
или s
5
и не вернуться), а состояния s
3
, s
4
, s
5
, s
6
, s
7
–
существенны (существенные состояния обведены жирными линия
ми).
При конечном числе состояний n для существования финальных
вероятностей необходимо и достаточно, чтобы из каждого существен%
ного состояния можно было (за какое%то число шагов) перейти в
Рис. 4.6. Граф, иллюстрирующий существенные и несущественные со%
стояния системы
s
1
s
2
s
3
s
4
s
5
s
6
s
7
89
каждое другое существенное. Граф, представленный на рис. 4.6, это
му условию не удовлетворяет (например, из существенного состоя
ния s
4
нельзя перейти в существенное состояние s
6
).
Несущественные состояния потому так и называются, что из каж
дого такого состояния система рано или поздно уйдет в какоето из
существенных и больше не вернется. Естественно, финальные веро
ятности для несущественных состояний равны нулю.
4.3. Теория массового обслуживания
Системой массового обслуживания (СМО) называется любая сис
тема, предназначенная для обслуживания какихлибо заявок (требо
ваний), поступающих на нее в случайные моменты времени. Примеры
СМО: телефонная станция; бюро ремонта; билетная касса; парикма
херская; ЭВМ; Центральная лаборатория методов НК предприятия.
Теория массового обслуживания занимается изучением случайных
процессов, протекающих в системах массового обслуживания.
Любое устройство, непосредственно занимающееся обслуживани
ем заявок, называется каналом обслуживания (или «прибором»).
Системы массового обслуживания бывают как одно, так и многока
нальными. Примеры одноканальной СМО – билетная касса с одним
кассиром, лаборатория НК с одной автоматизированной контрольной
установкой; примеры многоканальной СМО – та же касса с несколь
кими кассирами, та же лаборатория с несколькими (одинаковыми)
автоматизированными установками.
Различают СМО с отказами и СМО с очередью. В СМО с отказами
заявка, пришедшая в момент, когда все каналы заняты, получает
отказ, покидает СМО и в дальнейшем в процессе ее работы не уча
ствует. В СМО с очередью заявка, пришедшая в момент занятости
всех каналов, не покидает СМО, а становится в очередь и ждет, пока
не освободится какойнибудь канал. Число мест в очереди m может
быть как ограниченным, так и неограниченным. При m=0 СМО с оче
редью превращается в СМО с отказами. Очередь может иметь ограни
чение не только по количеству стоящих в ней заявок (длине очере
ди), но и по времени ожидания (такие СМО называются «системами с
нетерпеливыми клиентами»).
Системы массового обслуживания с очередью различаются не толь
ко по ограничениям очереди, но и по дисциплине обслуживания: об
служиваются ли заявки в порядке поступления, или в случайном
порядке, или же некоторые заявки обслуживаются вне очереди (так
называемые «СМО с приоритетом»). Приоритет может иметь несколь
ко градаций или рангов.

90
Аналитическое исследование СМО является наиболее простым,
если все потоки событий, переводящие ее из состояния в состояние, –
простейшие (стационарные пуассоновские). Это значит, что интер
валы между событиями в потоках имеют показательное распреде
ление с параметром, равным интенсивности соответствующего
потока. Для СМО это допущение означает, что как поток заявок,
так и поток обслуживаний – простейшие.
Из математики известно, что неотрицательная случайная вели
чина Х имеет показательное распределение, если ее плотность рас
пределения (равная плотности вероятности) имеет вид
0при 0;
()
при 0,
x
x
fx
ex
−μ
<
⎧
⎪
=
⎨
μ≥
⎪
⎩
где μ = const – параметр показательного распределения.
Для каждой случайной величины параметр показательного рас
пределения m имеет вполне определенное значение, например, f(x) =
= 5e
–5x
.
Основные характеристики случайной величины X, имеющей по
казательное распределение с параметром μ:
математическое ожидание
1
[] ;MX =
μ
дисперсия
2
1
[] ;DX =
μ
среднее квадратическое значение
1
[] ;Xσ=
μ
функция распределения
0при 0;
()
1при0.
x
x
Fx
ex
−μ
<
⎧
⎪
=
⎨
−≥
⎪
⎩
Под потоком обслуживания понимается поток заявок, обслужи
ваемых одна за другой одним непрерывно занятым каналом.
Этот поток оказывается простейшим, только если время обслу
живания заявки T
обсл
представляет собой случайную величину, име
ющую показательное распределение. Параметр этого распределения
μ и есть величина, обратная среднему времени обслуживания:
