Сударикова Е.В. Неразрушающий контроль в производстве. Часть 2

Подождите немного. Документ загружается.

Очевидно, что область A соответствует партиям, уровень качества

которых q < q

; область B – партиям, у которых q > q

. По условию

контроля партии, принадлежащие области A, должны по возможно

сти приниматься, а принадлежащие области B – браковаться. Если

учесть, что выборочные характеристики приближенно равны гене

ральным характеристикам, то естественным условием приемки можно

считать попадание случайной точки

(,)xs

в область ниже некоторой

нормативной прямой, проходящей между изодефектными линиями,

соответствующими партиям с уровнем качества q

и q

Таким образом, математическая запись сформулированного пра

вила приемки партии имеет вид

−

≥

(3.53)

где

−

≤ q

, и оперативная характеристика есть

() .

Lq P c

⎧⎫

−

=≥

⎨⎬

⎩⎭

(3.54)

Заметим, что

{}

PcPxcsT

⎧⎫

−

≥= +<

⎨⎬

⎩⎭

(3.55)

Рассмотрим выборочную функцию

,zxcs=+

(3.56)

такую, что

z = T, если случайная точка

(,),xs

определенная по результатам из

мерений, лежит на нормативной прямой H;

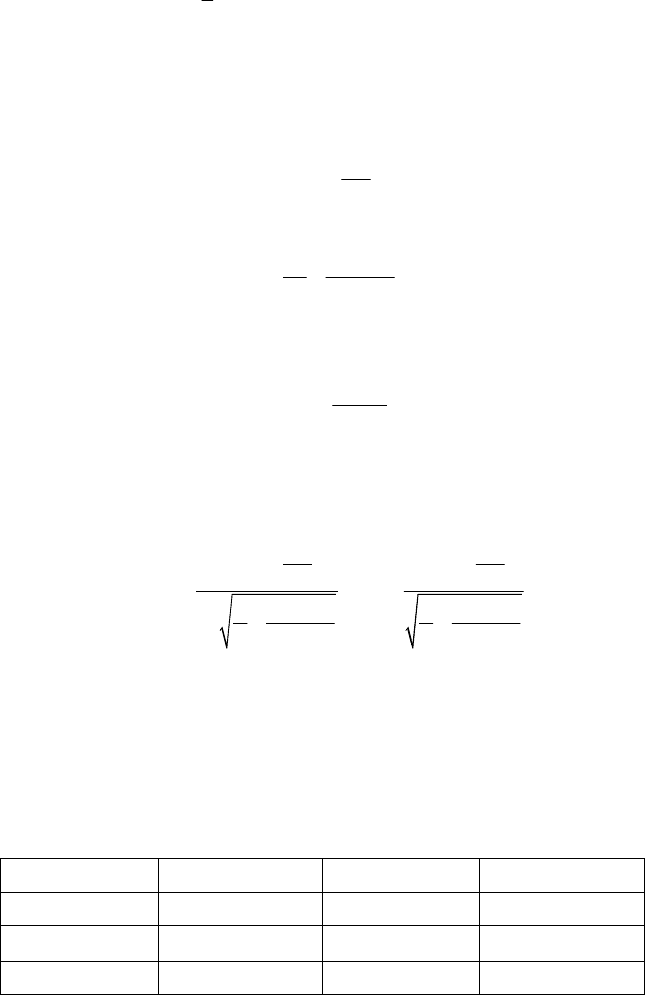
Рис. 3.14. Изодефектные линии и зоны приемки и браковки партий

s, s

z > T, если точка

(,)xs

лежит выше; и

z < T, если точка лежит ниже нормативной прямой H.

Для вычисления оперативной характеристики плана контроля

необходимо знать закон распределения случайной величины Z. До

казано, что при объеме выборки n > 5 величина Z имеет приближенно

нормальное распределение с математическим ожиданием

μ=μ+

(3.57)

и дисперсией

222

21,4

σσ

σ= +

−

(3.58)

где коэффициент K

находится по табл. 3.11 [5].

С учетом этого, вероятность (3.55) может быть вычислена

() ,

⎛⎞

−μ

=Φ

⎜⎟

⎝⎠

(3.59)

где q связано с μ и σ уравнением (3.50).

Путем несложных преобразований из уравнений (3.57)–(3.59)

получим

() .

21,4 21,4

nn nn

−

⎛⎞⎛⎞

−μ− −

⎜⎟⎜⎟

=Φ =Φ

⎜⎟⎜⎟

σ+ +

⎜⎟⎜⎟

−−

⎝⎠⎝⎠

(3.60)

Характерная особенность данного уравнения заключается в том,

что в него не входят значения генеральных характеристик μ и σ.

Таким образом, если требования к плану контроля сформулиро

ваны в виде q

, q

, α, β, то можно составить систему уравнений для

определения объема выборки и приемочного числа:

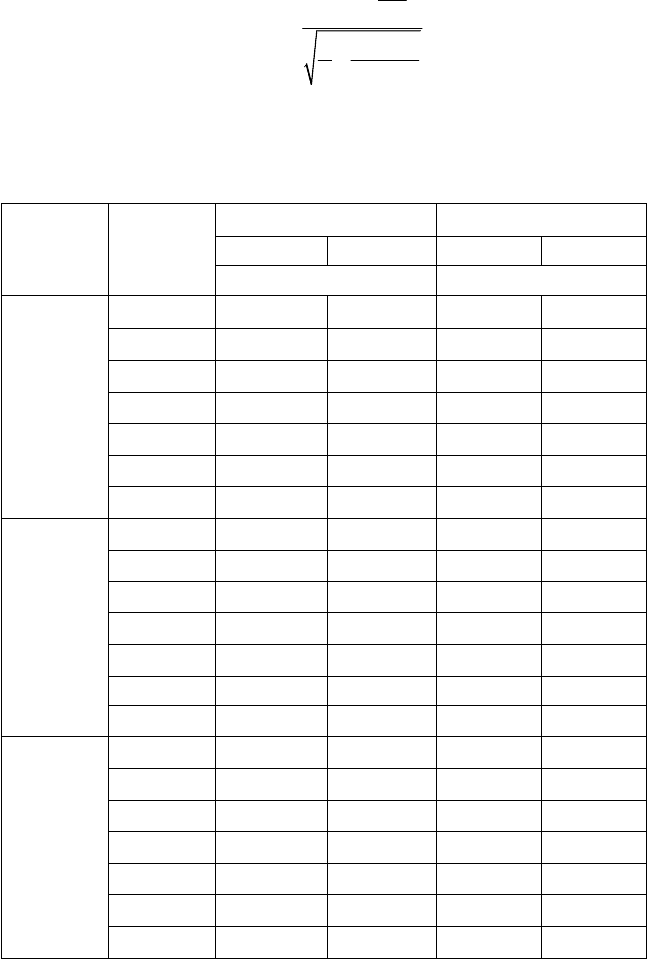
Таблица 3.11. Определение коэффициента K

по величине объема выборки

5460,102310,1

01820,152010,1

51810,103900,1

21,4

−

⎛⎞

−

⎜⎟

−α=Φ

⎜⎟

−

⎝⎠

(3.61)

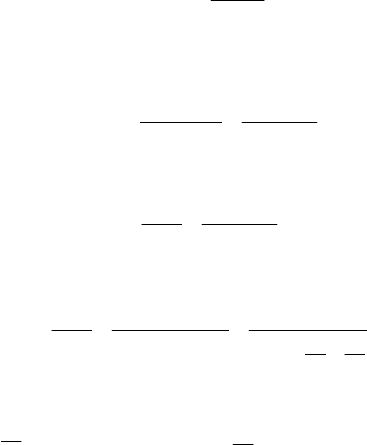
Таблица 3.12. Определение параметров плана контроля по заданным

приемочному q

и браковочному q

уровням качества

01,002,001,002,0

0,1070,0630,0813,0952,0

5,1960,0230,0591,0340,0

0,2400,0800,0801,0070,0

5,2530,0100,0650,0030,0

0,3540,0230,0620,0110,0

5,3350,

0240,0110,0400,0

0,4160,0150,0400,0100,0

0,1090,0111,0362,0522,0

5,1920,0930,0541,0411,0

0,2700,0110,0070,0050,0

5,2100,0200,

0030,0910,0

0,3130,0330,0110,0600,0

5,3140,0440,0400,0700,0

0,4160,0350,0100,0430,0

0,1070,0421,0822,0302,0

5,1730,0640,0611,0790,0

0,2010,0310,0150,0040,0

5,2200,0300,0910,0310,0

0,333

0,0530,0600,0400,0

5,3340,0640,0200,0100,0

0,4250,0650,0430,0230,0

21,4

−

⎛⎞

−

⎜⎟

β=Φ

⎜⎟

−

⎝⎠

(3.62)

Решение уравнений (3.61) и (3.62) в явном виде невозможно. Со

ставлены специальные таблицы [3], позволяющие по заданным q

для фиксированных значений α и β определить параметры плана

контроля, причем как для рассмотренных случаев, так и для случая

двустороннего ограничения контрольного параметра. Приведенная

табл. 3.12 ограничена объемом выборки n = 40.

Полученные уравнения и результаты расчетов справедливы так

же для случая одностороннего ограничения снизу, а выражение, фор

мулирующее критерий приемки партии, записывается в этом случае

в виде

−

≤

(3.63)

Таким образом, количественный контроль позволяет по сравне

нию с альтернативным существенно снизить объемы выборки. Од

нако применение его связано со значительными организационнотех

ническими трудностями, проведением замеров, сложных вычисле

ний. Для проведения таких работ на производстве необходимы высо

коквалифицированные специалисты. Это, безусловно, повышает сто

имость и снижает эффективность контроля.

3.8. Последующие оценки

при статистическом приемочном контроле

Существует множество способов анализа эффективности выбран

ного плана приемочного контроля. Один из них состоит в вычисле

нии различных статистических оценок по имеющейся информации о

приемке и браковке партии изделий и сопоставлении их либо с пара

метрами плана контроля, либо с требованиями к качеству продук

ции. Такие оценки называются последующими, так как они дела

ются после проведения контроля. Последующие оценки могут быть

использованы для решения целого ряда практически важных задач.

Например:

а) оценка среднего уровня входного качества q

вх

может служить

основанием для корректировки плана приемочного контроля в части

назначения приемочного уровня качества;

б) оценка среднего уровня выходного качества q

вых

может быть

использована для изменения объема выборки с целью повышения

среднего уровня качества товарной продукции.

Таким образом, необходимость учета накопленной в результате

контроля информации и вычисления последующих оценок очевид

на. Отметим, что эти оценки весьма просты и практически не требу

ют никаких затрат.

Наибольший интерес представляют так называемые несмещен

ные оценки, т.е. оценки, которые дают в среднем точные значения.

С точки зрения математической статистики оценка

случайной ве

личины Y является несмещенной, если

() (),YYμ=μ

(3.64)

где μ — символ математического ожидания.

Условимся понимать под оценкой любую функцию

()YX

, завися

щую от результатов испытаний x

, x

, …, x

и не зависящую в явном

виде от самой случайной величины.

Пусть производится контроль выборки изделий объемом n штук,

в результате которого определяется степень пригодности каждого

элемента выборки к дальнейшему использованию. Исход каждого

опыта можно рассматривать как реализацию некоторой случайной

величины X, принимающую нулевое значение, если изделие окажет

ся годным, и единицу, если изделие окажется дефектным.

Случайное сочетание X

нулей и единиц в данном конкретном опы

те определит числовое значение оценки

Обозначим через p(x

) вероятность того, что исходом опыта явит

ся значение x

, а следовательно, и

. Тогда, учитывая все возмож

ные K сочетаний нулей и единиц в n опытах, уравнение (3.64) в соот

ветствии с определением математического ожидания может быть за

писано в виде

()() ().

Yx px Y

=μ

∑

(3.65)

Уравнение (3.65) является исходным для получения несмещен

ных оценок.

Рассмотрим случай, когда приемочное число c равно нулю.

Пусть на контроль поданы партии, имеющие по N

изделий каж

дая, среди которых M

дефектных. При контроле партии мы накап

ливаем сведения не только о количестве дефектных изделий в выбор

ках, но и о количестве партий, имеющих в выборках по одному, по

два и т. д. дефектных изделий.

Покажем, как можно с помощью этих данных достаточно просто

вычислять интересующие нас оценки величин q

вх

и q

вых

Предположим, что среди проконтролированных партий одинако

вого объема N, от которых отбираются выборки одинакового объема

n, имеются группы партий с одинаковой засоренностью дефектными

изделиями. Рассмотрим одну из таких групп, состоящую из S партий.

Доля дефектности каждой партии постоянна и равна q.

В случае варианта контроля с разбраковкой в товар попадут

только те Nq дефектных изделий, которые были приняты в составе

непроконтролированных остатков партий. В выборках таких партий,

как следует из условия приемки, не должно быть дефектных изде

лий.

Среднее количество принятых партий составит SL(q), где L(q) –

вероятность приемки партии с уровнем качества q. Таким образом,

математическое ожидание числа пропущенных дефектных изделий

M′ во всех S партиях

() ().

MSLqNq

′

μ=

(3.66)

Если объем выборки равен n, то вероятность приемки партии из

делий при c=0 находится по уравнению

() .

−

(3.67)

Заметим, что вероятность получить в выборке одно дефектное из

делие равна

MNM NM

CC MC

−−

′

(3.68)

и, как следует из (3.68) и (3.67),

()

MCp

−

(3.69)

После преобразований получаем

() 1

Lq N M n

−−+

−− +

(3.70)

В случае малых q и больших N можно в знаменателе пренебречь

величиной

−

по сравнению с

−

Тогда

()

nqL q

−

(3.71)

Подставим (3.71) в (3.66):

() 1 1.

MSN pS p

nN n

⎛⎞ ⎛⎞

′

μ= − = −

⎜⎟ ⎜⎟

⎝⎠ ⎝⎠

(3.72)

Из математической статистики известно, что несмещенной оцен

кой для p

служит величина

(3.73)

где S

– количество партий среди S, в выборках которых обнаружено

одно дефектное изделие.

С учетом этого оценку для количества пропущенных дефектных

изделий M′

дадим в виде

⎛⎞

′

=−

⎜⎟

⎝⎠

(3.74)

Оценка выражения (3.74) является несмещенной, так как

() 1() 1 ().

MSSpM

⎛⎞ ⎛⎞

′′

μ=−μ=− =μ

⎜⎟ ⎜⎟

⎝⎠ ⎝⎠

Полученное уравнение справедливо для любой группы партий.

Поэтому суммарное среднее число принятых дефектных изделий во

всех принятых партиях равно

⎛⎞

′

=−

⎜⎟

⎝⎠

∑

(3.75)

где суммирование распространяется на все группы с различными N и n.

Получаемая несмещенная оценка для суммарного количества де

фектных изделий в принятой продукции справедлива также и для

варианта контроля без разбраковки.

Получим оценки для количества дефектных изделий в партиях,

поставляемых на контроль.

При контроле с разбраковкой эта оценка получается путем сумми

рования выражения (3.75) и числа дефектных изделий Y в разбрако

ванных партиях. Отметим, что в этом случае Y в каждой разбрако

ванной партии тождественно равно M. Тогда

MM Y

′

∑

(3.76)

В формуле (3.76) суммирование производится по всем партиям,

подвергнутым разбраковке.

Получим аналогичную оценку для количества предъявленных де

фектных изделий в случае контроля без разбраковки. Здесь мы рас

полагаем лишь информацией о количестве дефектных изделий в вы

борках.

Пусть во всех выборках поданных на контроль S партий объема N

с уровнем качества q обнаружено m

дефектных изделий.

Известно, что если в партии объемом N имеется M дефектных из

делий, то среднее значение числа дефектных единиц в выборке объе

мом n равно

(3.77)

Среднее количество дефектных изделий в S выборках

При

равнивая полученное выражение количеству m

дефектных изделий

в выборках S партий, находим оценку для M в одной партии:

(3.78)

откуда получаем оценку для общего числа

дефектных изделий

во всех S партиях:

(3.79)

Оценка является несмещенной.

Поскольку полученное решение справедливо для партий с любым

значением q, суммируя полученный результат по всем группам партий

с разными N и n, получим несмещенную оценку количества дефект

ных изделий в предъявленной на контроль продукции:

∑

(3.80)

Теперь несложно записать уравнения для вычисления входного и

выходного средних уровней качества.

1. При контроле с разбраковкой:

вх

;

ΣΣ

⎛⎞

−+

⎜⎟

⎝⎠

∑∑

(3.81)

вых

ΣΣ

⎛⎞

−

⎜⎟

′

⎝⎠

∑

(3.82)

где N

– общее количество предъявленных на контроль изделий.

2. При контроле без разбраковки:

вх

;

ΣΣ

∑

(3.83)

вых

ΣΣ

⎛⎞

−

⎜⎟

′

⎝⎠

′′

∑

(3.84)

где N′

– количество изделий во всех принятых партиях.

3.9. Непрерывный статистический приемочный контроль

Непрерывный приемочный контроль применяют в условиях мас

сового или серийного производства, когда изделия непрерывно по

ступают на контрольный пункт в последовательности, в которой они

производятся (способ «поток»), а формирование отдельных партий

для контроля невозможно или нецелесообразно.

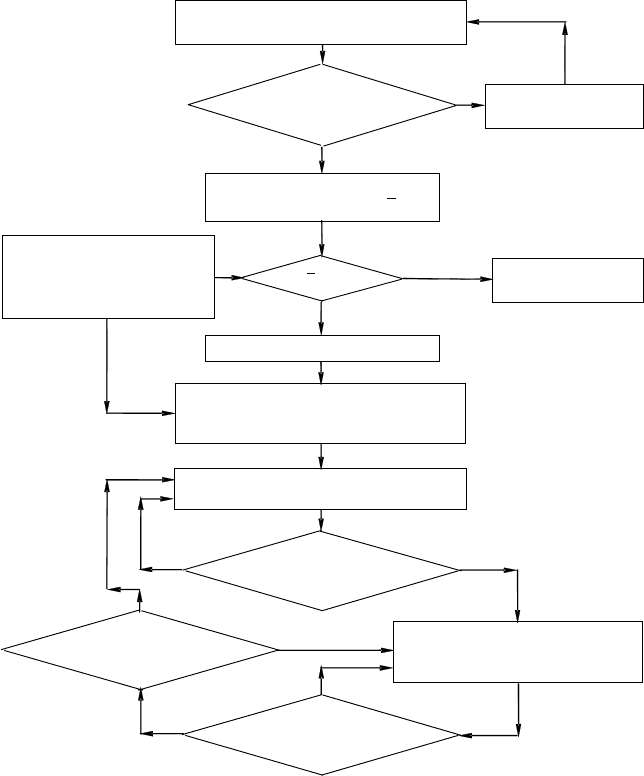
Общий алгоритм непрерывного статистического приемочного кон

троля показан на рис. 3.15.

Планы контроля выбирают в соответствии со стандартом

(СТ СЭВ 293–76, с 1979 г. введен в действие в качестве ГОСТ). Поря

док выбора приемочного уровня дефектности такой же, как при при

емочном контроле партий. Число изделий одного производственного

цикла выбирают из соображений, аналогичных выбору объема партии.

Стандарт определяет три общих уровня контроля, из которых

обычно используют уровень II, в более ответственных случаях – уро

вень III и в менее ответственных – уровень I.

По этим данным с помощью таблиц, приведенных в стандарте,

определяют параметры плана контроля и осуществляют процедуру

непрерывного контроля как чередование периодов сплошной и выбо

рочной проверок. Чем выше качество продукции, тем меньше удель

ный вес сплошного контроля. В то же время длительный период

сплошного контроля (невыполнение условий перехода к выборочно

му) означает, что качество продукции не соответствует приемочному

уровню дефектности. Поэтому в стандарте приведены численные зна

чения верхнего предела числа проверяемых изделий при сплошном

контроле, при превышении которого следует прекратить производ

ственный процесс и возобновить его только после проведения необ

ходимых коррекций.

Рис. 3.15. Общий алгоритм непрерывного статистического приемочно%

го контроля

K?>;=8BL AB0B8AB8G5A:89 0=0;87

B>G=>AB8 8 AB018;L=>AB8 B5E?@>F5AA0

@>8725AB8

>B;04:C ?@>F5AA0

?@545;8BL A@54=89 2E>4=>9

C@>25=L 45D5:B=>AB8

@8<5=8BL

A?;>H=>9 :>=B@>;L

#AB0=>28BLG8A;> 8745;89

>4=>3> ?@>872>4AB25==>3>

F8:;0, ?@85<>G=K9 C@>25=L

45D5:B=>AB8q

K1@0BLC@>25=L :>=B@>;O

#AB0=>28BL?0@0<5B@K ?;0=0

:>=B@>;O, :>MDD8F85=B 2K1>@>G=>AB8f,

4;8=C A5@88i

K?>;=8BL A?;>H=>9 :>=B@>;L

?>4@O4 ?@>872545==KE 8745;89

@>F5AA

>B;065==K9 8 AB018;L=K9

B> 8745;85 3>4=>5

i ?>A;54CNI8E 2K1>@:0E

?>4@O4 8745;8O 3>4=K5

K?>;=OBL 2K1>@>G=K9 :>=B@>;L

K1>@:0 >4=> A;CG09=>5 8745;85

87 1/f ?>4@O4 ?@>872545==KE

i 8745;89 ?>4@O4

3>4=K5