Stone M., Goldbart P. Mathematics for Physics: A Guided Tour for Graduate Students
Подождите немного. Документ загружается.

18.5 Further exercises and problems 705
Problem 18.24: If we define χ(h) = e
αx
φ(x), and F(x) = e
αx
f (x), then the Wiener–
Hopf equation
φ(x) − λ
∞
0
e
−|x−y|−α(x−y)
φ(y) dy = f (x), x > 0
becomes
χ(x) − λ
∞
0
e
−|x−y|
χ(y) dy = F(x), x > 0,
all mention of α having disappeared! Why then does our answer, worked out in such
detail, in Section 18.4.2, depend on the parameter α? Show that if α is small enough
that α + a is positive and α − a is negative, then φ(x) really is independent of α. (Hint:
what tacit assumptions about function spaces does our use of Fourier transforms entail?
How does the inverse Fourier transform of [(k + iα)
2
+ a
2
]
−1
vary with α?)

19
Special functions and complex variables
In this chapter we will apply complex analytic methods so as to obtain a wider view of
some of the special functions of mathematical physics than can be obtained from the real
axis. The standard text in this field remains the venerable Course of Modern Analysis of
E. T. Whittaker and G. N. Watson.
19.1 The Gamma function
We begin by examining how Euler’s “Gamma function” (z) behaves when z is allowed
to become complex. You probably have some acquaintance with this creature. The usual
definition is
(z) =
∞
0
t
z−1
e
−t
dt,Rez > 0 (definition A). (19.1)
The restriction on the real part of z is necessary to make the integral converge. We
can, however, analytically continue (z) to a meromorphic function on all of C.An
integration by parts, based on
d
dt
t
z
e
−t
= zt
z−1
e
−t
− t
z
e
−t
, (19.2)
shows that
t
z
e
−t
∞
0
= z
∞
0
t
z−1
e
−t
dt −
∞
0
t
z
e
−t
dt. (19.3)
The integrated out part vanishes at both limits, provided the real part of z is greater than
zero. Thus we obtain the recurrence relation
(z + 1) = z(z). (19.4)
Since (1) = 1, we deduce that
(n) = (n − 1)!, n = 1, 2, 3, ... (19.5)
706

19.1 The Gamma function 707
We can use the recurrence relation (19.4) to extend the definition of (z) to the left
half-plane, where the real part of z is negative. Choosing an integer n such that the real
part of z + n is positive, we write
(z) =
(z + n)
z(z + 1) ···(z + n − 1)
. (19.6)
We see that the extended (z) has poles at zero, and at the negative integers. The residue
of the pole at z =−n is (−1)
n
/n!.
We can also view the analytic continuation as an example of Taylor series subtraction.
Let us recall how this works. Suppose that −1 < Re x < 0. Then, from
d
dt
(t
x
e
−t
) = xt
x−1
e
−t
− t
x
e
−t
(19.7)
we have
t
x
e
−t
∞
= x
∞
dt t
x−1
e
−t
−
∞
dt t
x
e
−t
. (19.8)
Here we have cut off the integral at the lower limit so as to avoid the divergence near
t = 0. Evaluating the left-hand side and dividing by x we find
−
1
x
x
=
∞
dt t
x−1
e
−t
−
1
x
∞
dt t
x
e
−t
. (19.9)
Since, for this range of x,
−
1
x
x
=
∞
dt t
x−1
, (19.10)
we can rewrite (19.9)as
1
x
∞
dt t
x
e
−t
=
∞
dt t
x−1
e
−t
− 1
. (19.11)
The integral on the right-hand side of this last expression is convergent as → 0, so we
may safely take the limit and find
1
x
(x + 1) =
∞
0
dt t
x−1
e
−t
− 1
. (19.12)
Since the left-hand side is equal to (x), we have shown that
(x) =
∞
0
dt t
x−1
e
−t
− 1
, −1 < Re x < 0. (19.13)

708 19 Special functions and complex variables
Similarly, if −2 < Re x < −1, we can show that
(x) =
∞
0
dt t
x−1
e
−t
− 1 + t
. (19.14)
Thus the analytic continuation of the original integral is given by a new integral in which
we have subtracted exactly as many terms from the Taylor expansion of e
−t
as are needed
to just make the integral convergent at the lower limit.
Other useful identities, usually proved by elementary real-variable methods, include
Euler’s “Beta function” identity,
B(a, b)
def
=
(a)(b)
(a + b)
=
1
0
(1 − t)
a−1
t
b−1
dt (19.15)
(which, as the Veneziano formula, was the original inspiration for string theory) and
(z)(1 − z) = πcosec π z. (19.16)
The proofs of both formulæ begin in the same way: set t = y
2
, x
2
, so that
(a)(b) = 4
∞
0
y
2a−1
e
−y
2
dy
∞
0
x
2b−1
e
−x
2
dx
= 4
∞
0
∞
0
e
−(x
2
+y
2
)
x
2b−1
y
2a−1
dx dy
= 2
∞
0
e
−r
2
(r
2
)
a+b−1
d(r
2
)
π/2
0
sin
2a−1
θ cos
2b−1
θ dθ.
We have appealed to Fubini’s theorem twice: once to turn a product of integrals into
a double integral, and once (after setting x = r cos θ, y = r sin θ ) to turn the double
integral back into a product of decoupled integrals. In the second factor of the third line
we can now change variables to t = sin
2
θ and obtain the Beta function identity. If, on
the other hand, we put a = 1 − z, b = z, we have
(z)(1 − z) = 2
∞
0
e
−r
2
d(r
2
)
π/2
0
cot
2z−1
θ dθ = 2
π/2
0
cot
2z−1
θ dθ. (19.17)
Now set cot θ = ζ . The last integral then becomes (see Exercise 18.1):
2
∞
0
ζ
2z−1
ζ
2
+ 1
dζ = π cosec π z,0< z < 1, (19.18)
establishing the claimed result. Although this last integral has a restriction on the range
of z (19.16) holds for all z by analytic continuation. If we put z = 1/2, we find that
(
(1/2)
)
2
= π. Because the definition-A integral for (1/2) is manifestly positive, the
positive square root is the correct one, and
(1/2) =
√
π. (19.19)

19.1 The Gamma function 709
C
Im(t)
Re(t
)
Figure 19.1 Definition B contour for (z).
The integral in definition A for (z) is only convergent for Re z > 0. A more powerful
definition, involving an integral that converges for all z, is (see Figure 19.1)
1
(z)
=
1
2πi
C
e
t
t
z
dt (definition B). (19.20)
Here, C is a contour originating at z =−∞−i, below the negative real axis (on which
a cut serves to make t
−z
single valued) rounding the origin, and then heading back to
z =−∞+i, this time staying above the cut. We take arg t to be +π immediately
above the cut, and −π immediately below it. This new definition is due to Hankel.
For z an integer, the cut is unnecessary and we can replace the contour by a circle
about z = 0 and so find
1
(0)
= 0;
1
(n)
=
1
(n − 1)!
, n > 0. (19.21)
Thus, definitions A and B agree on the integers. It is less obvious that they agree for all
z. A hint that this is true stems from integrating by parts
1
(z)
=
1
2πi
e
t
(z − 1)t
z−1
−∞+i
−∞−i
+
1
(z − 1)2π i
C
e
t
t
z−1
dt =
1
(z − 1)(z − 1)
.
(19.22)
The integrated-out part vanishes because e
t
is zero at −∞. Thus the “new” Gamma
function obeys the same functional relation as the “old” one.
To show that the equivalence holds for non-integer z we will examine the definition-B
expression for (1 − z):
1
(1 − z)
=
1
2πi
C
e
t
t
z−1
dt. (19.23)
We will assume initially that Re z > 0, so that there is no contribution to the integral from
the small circle about the origin. We can therefore focus on the contribution from the
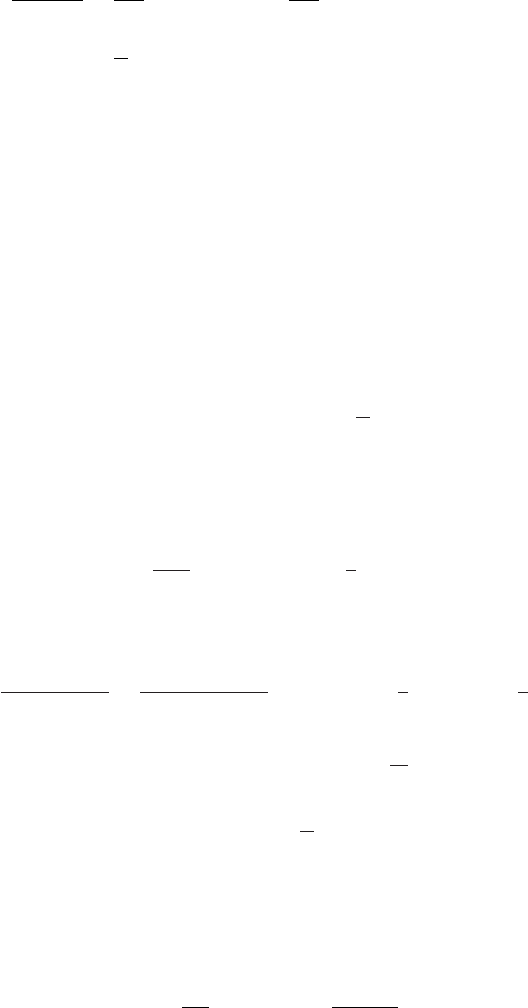
710 19 Special functions and complex variables
discontinuity across the cut, which is
1
(1 − z)
=
1
2πi
C
e
t
t
z−1
dt =−
1
2πi
(2i sin π(z − 1))
∞
0
t
z−1
e
−t
dt
=
1
π
sin πz
∞
0
t
z−1
e
−t
dt. (19.24)
The proof is then completed by using (z)(1 − z) = π cosec πz, which we proved
using definition A, to show that, under definition A, the right-hand side is indeed equal
to 1/(1 − z). We now use the uniqueness of analytic continuation, noting that if two
analytic functions agree on the region Re z > 0, then they agree everywhere.
Infinite product for (z)
The function (z) has poles at z = 0, −1, −2, ..., and therefore
(
z(z)
)
−1
=
(
(z + 1)
)
−1
has zeros as z =−1, −2, ...Furthermore, the integral in definition B con-
verges for all z, and so 1/(z) has no singularities in the finite z plane, i.e. it is an entire
function. This means that we can use the infinite product formula from Section 18.3.2:
g(z) = g(0)e
cz
∞
9
j=1
1 −
z
z
j
e
z/z
j
. (19.25)
We need to recall the definition of the Euler–Mascheroni constant γ =−
(1) =
0.5772157 ..., and that (1) = 1. Then
1
(z)
= ze
γ z
∞
9
n=1
1 +
z
n
e
−z/n
. (19.26)
We can use this formula to compute
1
(z)(1 − z)
=
1
(−z)(z)(−z)
= z
∞
9
n=1
1 +
z
n
e
−z/n
1 −
z
n
e
z/n
= z
∞
9
n=1
1 −
z
2
n
2
=
1
π
sin πz,
and so obtain another (but not really independent) demonstration that
(z)(1 − z) = πcosec π z.
Exercise 19.1: Starting from the infinite product formula for (z), show that
d
2
dz
2
ln (z) =
∞
n=0
1
(z + n)
2
.

19.2 Linear differential equations 711
(Compare this “half series” with the expansion
π
2
cosec
2
πz =
∞
n=−∞
1
(z + n)
2
.)
19.2 Linear differential equations
When linear differential equations have coefficients that are meromorphic functions,
their solutions can be extended off the real line and into the complex plane. The broader
horizon then allows us to see much more of their structure.
19.2.1 Monodromy
Consider the linear differential equation
Ly ≡ y
+ p(z )y
+ q(z)y = 0, (19.27)
where p and q are meromorphic. Recall that the point z = a is a regular singular point
of the equation if p or q is singular there but
(z − a)p(z), (z − a)
2
q(z) (19.28)
are both analytic at z = a. We know, from the explicit construction of power series
solutions, that near a regular singular point y is a sum of functions of the form y =
(z − a)
α
ϕ(z) or y = (z − a)
α
(ln(z − a)ϕ(z) + χ(z)), where both ϕ(z) and χ(z) are
analytic near z = a. We now examine this fact from a more topological perspective.
Suppose that y
1
and y
2
are linearly independent solutions of Ly = 0. Start from some
ordinary (non-singular) point of the equation and analytically continue the solutions
round the singularity at z = a and back to the starting point. The continued functions ˜y
1
and ˜y
2
will not in general coincide with the original solutions but, still being solutions
of the equation, they must be linear combinations of them. Therefore
˜y
1
˜y
2
=
a
11
a
12
a
21
a
22
y
1
y
2
, (19.29)
for some constants a
ij
. By a suitable redefinition of y
1,2
we may either diagonalize this
monodromy matrix to find
˜y
1
˜y
2
=
λ
1
0
0 λ
2
y
1
y
2
(19.30)
or, if the eigenvalues coincide and the matrix is not diagonalizable, reduce it to a
Jordan form
˜y
1
˜y
2
=
λ 1
0 λ
y
1
y
2
. (19.31)

712 19 Special functions and complex variables
These matrix equations are satisfied, in the diagonalizable case, by functions of the form
y
1
= (z −a)
α
1
ϕ
1
(z), y
2
= (z −a)
α
2
ϕ
2
(z), (19.32)
where λ
k
= e
2πiα
k
, and ϕ
k
(z) is single valued near z = a. In the Jordan-form case we
must have
y
1
= (z −a)
α
ϕ
1
(z) +
1
2πiλ
ln(z − a)ϕ
2
(z)
, y
2
= (z −a)
α
ϕ
2
(z), (19.33)
where, again, the ϕ
k
(z) are single-valued. Notice that coincidence of the monodromy
eigenvalues λ
1
and λ
2
does not require the exponents α
1
and α
2
to be the same, only that
they differ by an integer. This is the same Frobenius condition that signals the presence
of a logarithm in the traditional series solution.
The occurrence of fractional powers and logarithms in solutions near a regular singular
point is therefore quite natural.
19.2.2 Hypergeometric functions
Most of the special functions of mathematical physics are special cases of the
hypergeometric function F(a, b; c; z), which may be defined by the series
F(a, b; c; z) = 1 +
a.b
1.c
z +
a(a + 1)b(b + 1)
2!c(c + 1)
z
2
+
+
a(a + 1)(a + 2)b(b + 1)(b + 2)
3!c(c + 1)(c + 2)
z
3
+···
=
(c)
(a)(b)
∞
n=0
(a + n)(b + n)
(c + n)(1 + n)
z
n
. (19.34)
For general values of a, b, c, this series converges for |z| < 1, the singularity restricting
the convergence being a branch point at z = 1.
Examples:
(1 + z)
n
= F(−n, b; b; −z), (19.35)
ln(1 + z) = zF(1, 1; 2; −z), (19.36)
z
−1
sin
−1
z = F
1
2
,
1
2
;
3
2
; z
2
, (19.37)
e
z
= lim
b→∞
F(1, b;1/b; z/b), (19.38)
P
n
(z) = F
−n, n + 1; 1;
1 − z
2
, (19.39)
where in the last line P
n
is the Legendre polynomial.

19.2 Linear differential equations 713
For future reference, note that expanding the integrand on the right-hand side as a
power series in z and integrating term by term shows that F(a, b; c; z) has the integral
representation
F(a, b; c; z) =
(c)
(b)(c − b)
1
0
(1 − tz)
−a
t
b−1
(1 − t)
c−b−1
dt. (19.40)
If Re c > Re (a + b), we may set z = 1 in this integral to get
F(a, b; c;1) =
(c)(c − a − b)
(c − a)(c − b)
. (19.41)
The hypergeometric function is a solution of the second-order differential equation
z(1 − z)y
+[c − (a + b + 1)z]y
− aby = 0. (19.42)
This equation has regular singular points at z = 0, 1, ∞. Provided that 1 − c is not an
integer, the general solution is
y = AF(a, b; c; z ) + Bz
1−c
F(b − c + 1, a − c +1; 2 − c; z). (19.43)
A differential equation possessing only regular singular points is known as a Fuchsian
equation. The hypergeometric equation is a particular case of the general Fuchsian
equation with three
1
regular singularities at z = z
1
, z
2
, z
3
. This equation is
y
+ P(z)y
+ Q(z)y = 0, (19.44)
1
The Fuchsian equation with two regular singularities is
y
+ p(z)y
+ q(z)y = 0
with
p(z) =
1 − α − α
z − z
1
+
1 + α + α
z − z
2
,
q(z) =
αα
(z
1
− z
2
)
2
(z − z
1
)
2
(z − z
2
)
2
.
Its general solution is
y = A
z − z
1
z − z
2
α
+ B
z − z
1
z − z
2
α
.

714 19 Special functions and complex variables
where
P(z) =
1 − α − α
z − z
1
+
1 − β − β
z − z
2
+
1 − γ − γ
z − z
3
Q(z) =
1
(z − z
1
)(z − z
2
)(z − z
3
)
×
(z
1
− z
2
)(z
1
− z
3
)αα
z − z
1
+
(z
2
− z
3
)(z
2
− z
1
)ββ
z − z
2
+
(z
3
− z
1
)(z
3
− z
2
)γ γ
z − z
3
. (19.45)
The parameters are subject to the constraint α +β +γ +α
+β
+γ
= 1, which ensures
that z =∞is not a singular point of the equation. This equation is sometimes called
Riemann’s P-equation. The P probably stands for Papperitz, who discovered it.
The indicial equation relative to the regular singular point at z
1
is
r(r − 1) + (1 − α − α
)r + αα
= 0, (19.46)
and has roots r = α, α
. From this, we deduce that Riemann’s equation has solutions that
behave like (z −z
1
)
α
and (z −z
1
)
α
near z
1
. Similarly, there are solutions that behave like
(z − z
2
)
β
and (z −z
2
)
β
near z
2
, and like (z − z
3
)
γ
and (z −z
3
)
γ
near z
3
. The solution
space of Riemann’s equation is traditionally denoted by the Riemann “P” symbol
P
⎧
⎨
⎩
z
1
z
2
z
3
αβγz
α
β
γ
⎫
⎬
⎭
(19.47)
where the six quantities α, β, γ , α
, β
, γ
are called the exponents of the solution. A
particular solution is
y =
z − z
1
z − z
2
α
z − z
3
z − z
2
γ
× F
α +β + γ , α + β
+ γ ;1+ α − α
;
(z − z
1
)(z
3
− z
2
)
(z − z
2
)(z
3
− z
1
)
. (19.48)
By permuting the triples (z
1
, α, α
), (z
2
, β, β
), (z
3
, γ , γ
), and within them interchanging
the pairs α ↔ α
, γ ↔ γ
, we may find a total
2
of 6 × 4 = 24 solutions of this form.
They are called the Kummer solutions. Only two of them can be linearly independent,
and a large part of the theory of special functions is devoted to obtaining the linear
relations between them.
2
The interchange β ↔ β
leaves the hypergeometric function invariant, and so does not give a new solution.
