Stone M., Goldbart P. Mathematics for Physics: A Guided Tour for Graduate Students

Подождите немного. Документ загружается.

18.4 Wiener–Hopf equations II 695

If N ≥ 0, and we break this equation into its positive and negative powers, we find

−

]

= λz

(z)X

−

]

−

=−Y

−

(z). (18.109)

From the first of these equations we can read off the desired x

as the positive-power

Laurent coefficients of

(z) =[Y

−

]

(λz

(z))

−1

. (18.110)

As a byproduct, the second allows us to find the coefficient y

−n

of Y

−

(z). Observe that

there is a condition on Y

for this to work: the power series expansion of λz

(z)X

starts with z

, and so for a solution to exist the first N terms of

(

−

)

as a power series

in z must be zero. The given vector y

must therefore satisfy N consistency conditions.

A formal way of expressing this constraint begins by observing that it means that the

range of the operator A represented by the matrix a

n−m

falls short, by N dimensions, of

being the entire space of possible y

. This is exactly the situation that the notion of a

“co-kernel” is intended to capture. Recall that if A : V → V , then Coker A = V /Im A.

We therefore have

dim [Coker A]=N .

When N < 0, on the other hand, we have

(z)q

−

(z)]

=[λz

−|N |

(z)X

(z)]

(z)q

−

(z)]

−

=−Y

−

(z)q

−

(z) +[λz

−|N |

(z)X

(z)]

−

. (18.111)

Here the last term in the second equation contains no more than N terms. Because

of the z

−|N |

, we can add to X

any multiple of Z

(x) = z

(z)]

−1

for n =

0, ..., N − 1, and still have a solution. Thus the solution is not unique. Instead, we

have dim [Ker (A)]=|N |.

We have therefore shown that

Index (A)

def

= dim (Ker A) − dim (Coker A) =−N .

This connection between a topological quantity – in the present case the winding number

– and the difference in dimension of the kernel and co-kernel is an example of an index

theorem.

We now need to show that we can indeed factorize A(z) in the desired manner. When

A(z) is a rational function, the factorization is straightforward: if

A(z) = C

(z − a

)

(z − b

)

, (18.112)

696 18 Applications of complex variables

we simply take

(z) =

|>0

(1 − z/a

)

|>0

(1 − z/b

)

, (18.113)

where the products are over the linear factors corresponding to poles and zeros outside

the unit circle, and

−

(z) =

|<0

(1 − b

/z)

|<0

(1 − a

/z)

, (18.114)

containing the linear factors corresponding to poles and zeros inside the unit circle. The

constant λ and the power z

in Equation (18.106) are the factors that we have extracted

from the right-hand sides of (18.113) and (18.114), respectively, in order to leave 1’s as

the first term in each linear factor.

More generally, we take the logarithm of

−N

A(z) = λq

(z)(q

−

(z))

−1

(18.115)

to get

ln[z

−N

A(z)]=ln[λq

(z)]−ln[q

−

(z)], (18.116)

where we desire ln[λq

(z)] to be the boundary value of a function analytic within the

unit circle, and ln[q

−

(z)]the boundary value of a function analytic outside the unit circle

and with q

−

(z) tending to unity as |z|→∞. The factor of z

−N

in the logarithm serves

to undo the winding of the argument of A(z), and results in a single-valued logarithm on

the unit circle. Plemelj now shows that

Q(z) =

2πi

|z|=1

ln[ζ

−N

A(ζ )]

ζ − z

dζ (18.117)

provides us with the desired factorization. This function Q(z) is everywhere analytic

except for a branch cut along the unit circle, and its branches, Q

within and Q

−

without

the circle, differ by ln[z

−N

A(z)]. We therefore have

λq

(z) = e

(z)

−

(z) = e

−

(z)

. (18.118)

The expression for Q as an integral shows that Q(z) ∼ const./z as |z| goes to infinity

and so guarantees that q

−

(z) has the desired limit of unity there.

18.4 Wiener–Hopf equations II 697

The task of finding this factorization is known as the scalar Riemann–Hilbert problem.

In effect, we are decomposing the infinite matrix

A =

⎛

⎜

⎝

··· a

···

··· a

−1

···

··· a

−2

−1

···

⎞

⎟

⎠

(18.119)

into the product of an upper triangular matrix

U = λ

⎛

⎜

⎝

··· 1 q

···

··· 01q

···

··· 00 1···

⎞

⎟

⎠

, (18.120)

a lower triangular matrix L, where

−1

⎛

⎜

⎝

··· 100···

··· q

−

−1

10···

··· q

−

−2

−

−1

1 ···

⎞

⎟

⎠

(18.121)

has 1’s on the diagonal, and a matrix 

which is zero everywhere except for a line of

1’s located N steps above the main diagonal. The set of triangular matrices with unit

diagonal form a group, so the inversion required to obtain L results in a matrix of the

same form. The resulting Birkhoff factorization

A = L

U, (18.122)

is an infinite-dimensional extension of the Gauss–Bruhat (or generalized LU) decom-

position of a matrix. The finite-dimensional Gauss–Bruhat decomposition provides a

factorization of a matrix A ∈ GL(n) as

A = LU, (18.123)

where L is a lower triangular matrix with 1’s on the diagonal, U is an upper triangular

matrix with no zeros on the diagonal and  is a permutation matrix, i.e. a matrix that

permutes the basis vectors by having one entry of 1 in each row and in each column, and

all other entries zero. Our present 

is playing the role of such a matrix. The matrix

 is uniquely determined by A. The L and U matrices become unique if L is chosen so

that 

L is also lower triangular.

698 18 Applications of complex variables

18.4.2 Wiener–Hopf integral equations

We now carry over our insights from the simpler sum equations to Weiner–Hopf integral

equations



∞

K(x − y)φ(y) dy = f (x), x > 0, (18.124)

by imagining replacing the unit circle by a circle of radius R, and then taking R →∞

in such a way that the sums go over to integrals. In this way many features are retained:

the problem is still solved by factorizing the Fourier transform

;

K(k) =



∞

−∞

K(x)e

ikx

dx (18.125)

of the kernel, and there remains an index theorem

dim (Ker K) − dim (Coker K ) =−N , (18.126)

but N now counts the winding of the phase of

;

K(k) as k ranges over the real axis:

N =

2π

arg

;

k=+∞

k=−∞

. (18.127)

One restriction arises though: we will require K to be of the form

K(x − y) = δ(x − y) + g(x −y) (18.128)

for some continuous function g(x). Our discussion is therefore being restricted to

Wiener–Hopf integral equations of the second kind.

The restriction comes about because we will seek to obtain a factorization of

;

K as

τ(κ)

;

K(k) = exp{Q

(k) − Q

−

(k)}=q

(k)(q

−

(k))

−1

(18.129)

where q

(k) ≡ exp{Q

(k)} is analytic and non-zero in the upper half k-plane and

−

(k) ≡ exp{Q

−

(k)} analytic and non-zero in the lower half-plane. The factor τ(κ) is

a phase such as

τ(k) =



k + i

k − i



, (18.130)

which winds −N times and serves to undo the +N phase winding in

;

K. The Q

(k) will

be the boundary values from above and below the real axis, respectively, of

Q(k) =

2πi



∞

−∞

ln[τ(κ)

;

K(κ)]

κ − k

dκ. (18.131)

18.4 Wiener–Hopf equations II 699

The convergence of this infinite integral requires that ln[τ(κ)

;

K(k)] go to zero at infinity,

or, in other words,

lim

k→∞

;

K(k) = 1. (18.132)

This, in turn, requires that the original K(x) contain a delta function.

Example: We will solve the problem

φ(x) − λ



∞

−|x−y|−α(x−y)

φ(y) dy = f (x), x > 0. (18.133)

We require that 0 <α<1. The upper bound on α is necessary for the integral kernel

to be bounded. We will also assume for simplicity that λ<1/2. Following the same

strategy as in the sum case, we extend the integral equation to the entire range of x by

writing

φ(x) − λ



∞

−|x−y|−α(x−y)

φ(y) dy = f (x) + g(x), (18.134)

where f (x) is non-zero only for x > 0 and g(x) is non-zero only for x < 0. The Fourier

transform of this equation is



(k + iα)

+ a

(k + iα)

+ 1



;

(k) =

;

(k) +;g

−

(k), (18.135)

where a

= 1 −2λ and the ± subscripts are to remind us that

;

φ(k) and

;

f (k) are analytic

in the upper half-plane, and ;g(k) in the lower. We will use the notation H

for the space

of functions analytic in the upper half plane, and H

−

for functions analytic in the lower

half-plane, and so

;

(k),

;

f (

k) ∈ H

, ;g

−

(k) ∈ H

−

. (18.136)

We can factorize

;

K(k) =

(k + iα)

+ a

(k + iα)

+ 1

[k + i(α − a)]

[k + i(α − 1)]

[k + i(α + a)]

[k + i(α + 1)]

. (18.137)

Now suppose that a is small enough that α ± a > 0 and so the numerator has two zeros

in the lower half-plane, and the numerator has one zero in each of the upper and lower

half-planes. The change of phase in

;

K(k) as we go from minus to plus infinity is therefore

−2π, and so the index is N =−1. We should therefore multiply

;

K by

τ(k) =



k + i

k − i



−1

(18.138)

700 18 Applications of complex variables

before seeking to break it into its q

factors. We can however equally well take

τ(k) =



k + i(α − 1)

k + i(α − a)



(18.139)

as this also undoes the winding and allows us to factorize with

−

(k) = 1, q

(k) =



k + i(α + a)

k + i(α + 1)



. (18.140)

The resultant equation analogous to (18.108) is therefore



k + i(α + a)

k + i(α + 1)



;



k + i(α − 1)

k + i(α − a)



;



k + i(α − 1)

k + i(α − a)



−

;

= (τq

−

)

;

+ τ q

−

. (18.141)

The second line of this equation shows the interpretation of the first line in terms of the

objects in the general theory. The left-hand side is in H

– i.e. analytic in the upper

half-plane. The first term on the right is also in H

. (We are lucky. More generally it

would have to be decomposed into its H

parts.) If it were not for the τ(κ), the last term

would be in H

−

, but it has a potential pole at k =−i(α − a). We therefore remove this

pole by subtracting a term

−

k + i(α − a)

(an element of H

) from each side of the equation before projecting onto the H

parts.

After projecting, we find that



k + i(α + a)

k + i(α + 1)



;

−



k + i(α − 1)

k + i(α − a)



;

−

k + i(α − a)

= 0,

−



k + i(α − 1)

k + i(α − a)



−

k + i(α − a)

= 0. (18.142)

We solve for

;

(k) and ;g

−

(k):

;

(k) =



(k + iα)

+ 1

(k + iα)

+ a



;

−

− β



k + i(α + 1)

(k + iα)

+ a



−

(k) =

k + i(α − 1)

. (18.143)

Observe that g

−

(k) is always in H

−

because its only singularity is in the upper half-plane

for any β. The constant β is therefore arbitrary. Finally, we invert the Fourier transform,

using



θ(x)e

−αx

sinh ax



=−

(k + iα)

+ a

, (α ±a)>0, (18.144)

18.5 Further exercises and problems 701

to find that

φ(x) = f (x) −

2λ



−α(x−y)

sinh a(x − y)f (y) dy

+ β





(a − 1)e

−(α+a)x

+ (a + 1)e

−(α−a)x



, (18.145)

where β



(proportional to β) is an arbitrary constant.

By taking α in the range −1 <α<0 with (α ± a)<0, we make the index to be

N =+1. We will then find there is condition on f (x) for the solution to exist. This

condition is, of course, that f (x) be orthogonal to the solution

(x) =



(a − 1)e

−(α+a)x

+ (a + 1)e

−(α−a)x



(18.146)

of the homogeneous adjoint problem, this being the f (x) = 0 case of the α>0 problem

that we have just solved.

18.5 Further exercises and problems

Exercise 18.18: Contour integration: Use the calculus of residues to evaluate the

following integrals:



2π

dθ

(a + b cos θ)

,0< b < a



2π

cos

3θ

1 − 2a cos 2θ + a

dθ ,0< a < 1



∞

(1 + x

)

dx, −1 <α<2.

These are not meant to be easy! You will have to dig for the residues.

Answers:

2πa

− b

)

3/2

π(a

+ 1)

− 1

π(1 − a + a

)

a − 1

π(1 − α)

4 cos(πα/2)

Exercise 18.19: By considering the integral of

f (z ) = ln(1 − e

2iz

) = ln(−2ie

sin z)

702 18 Applications of complex variables

+ iY



Figure 18.12 Indented rectangle.

around the indented rectangle in Figure 18.12, with vertices 0, π, π +iY , iY , and letting

Y become large, evaluate the integral

I =



ln(sin x) dx.

Explain how the fact that  ln  → 0as → 0 allows us to ignore contributions from

the small indentations. You should also provide justification for any other discarded

contributions. Take care to make consistent choices of the branch of the logarithm,

especially if expanding ln(−2ie

sin x) = ix + ln 2 + ln(sin x) + ln(−i).

(Ans: −π ln 2.)

Exercise 18.20: By integrating a suitable function around the quadrant containing the

point z

= e

iπ/4

, evaluate the integral

I(α) =



∞

α−1

1 + x

dx 0 <α<4.

It should only be necessary to consider the residue at z

(Ans: (π/4)cosec (π α/4).)

Exercise 18.21: In Section 5.5.1 we considered the causal Green function for the damped

harmonic oscillator

G(t) =





−γ t

sin(t), t > 0,

0, t < 0,

and showed that its Fourier transform



∞

−∞

iωt

G(t) dt =



− (ω + iγ)

(18.147)

18.5 Further exercises and problems 703

had no singularities in the upper half-plane. Use Jordan’s lemma to compute the inverse

Fourier transform

2π



∞

−∞

−iωt



− (ω + iγ)

dω,

and verify that it reproduces G(t).

Problem 18.22: Jordan’s lemma and one-dimensional scattering theory. In Problem 4.13

we considered the one-dimensional scattering problem solutions

(x) =



ikx

+ r

(k)e

−ikx

, x ∈ L,

(k)e

ikx

, x ∈ R,

k > 0



(k)e

ikx

, x ∈ L,

ikx

+ r

(k)e

−ikx

, x ∈ R,

k < 0

and claimed that the bound-state contributions to the completeness relation were given

in terms of the reflection and transmission coefficients as



bound

∗

(x)ψ



) =−



∞

−∞

2π

(k)e

−ik(x+x



)

, x, x



∈ L,

=−



∞

−∞

2π

(k)e

−ik(x−x



)

, x ∈ L, x



∈ R,

=−



∞

−∞

2π

(k)e

−ik(x−x



)

, x ∈ R, x



∈ L,

=−



∞

−∞

2π

(k)e

−ik(x+x



)

, x, x



∈ R.

The eigenfunctions

(+)

(x) =



ikx

+ r

(k)e

−ikx

, x ∈ L,

(k)e

ikx

, x ∈,

and

(−)

(x) =



(k)e

ikx

, x ∈ L,

ikx

+ r

(k)e

−ikx

, x ∈ R,

are initially refined for k real and positive (ψ

(+)

)orfork real and negative (ψ

(−)

but they separately have analytic continuations to all of k ∈ C. The reflection and

transmission coefficients r

L,R

(k) and t

L,R

(k) are also analytic functions of k, and obey

L,R

(k) = r

∗

L,R

(−k

∗

), t

L,R

(k) = t

∗

L,R

(−k

∗

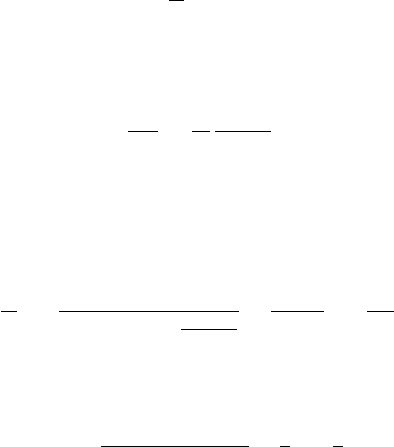
704 18 Applications of complex variables

(a) By inspecting the formulæ for ψ

(+)

(x), show that the bound states ψ

(x), with

=−κ

, are proportional to ψ

(+)

(x) evaluated at points k = i κ

on the positive

imaginary axis at which r

(k) and t

(k) simultaneously have poles. Similarly show

that these same bound states are proportional to ψ

(−)

(x) evaluated at points −iκ

on the negative imaginary axis at which r

(k) and t

(k) have poles. (All these

functions ψ

(±)

(x), r

R,L

(k), t

R,L

(k), may have branch points and other singularities

in the half-plane on the opposite side of the real axis from the bound-state poles.)

(b) Use Jordan’s lemma to evaluate the Fourier transforms given above in terms of the

position and residues of the bound-state poles. Confirm that your answers are of

the form



∗

[sgn(x)]e

−κ

|x|

[sgn(x



)]e

−κ



as you would expect for the bound-state contribution to the completeness relation.

Exercise 18.23: Lattice Matsubara sums. Let ω

= exp{iπ(2n + 1)/N }, for n =

0, ..., N − 1, be the N -th roots of (−1). Show that, for suitable analytic functions

f (z ), the sum

S =

N −1



n=0

f (ω

)

can be written as an integral

S =

2πi



+ 1

f (z ).

Here C consists of a pair of oppositely oriented concentric circles. The annulus formed

by the circles should include all the roots of (−1), but exclude all singularites of f . Use

this result to show that, for N even,

N −1



n=0

sinh E

sinh

E + sin

(2n+1)π

cosh E

tanh

Let N →∞while scaling E → 0 in some suitable manner, and hence show that

∞



n=−∞

+[(2n + 1)π ]

tanh

(Hint: if you are careless, you will end up differing by a factor of two from this last

formula. There are two regions in the finite sum that tend to the infinite sum in the large

N limit.)