Stone M., Goldbart P. Mathematics for Physics: A Guided Tour for Graduate Students
Подождите немного. Документ загружается.


17.7 Further exercises and problems 665
with the ± being selected depending on whether n is odd or even. Where would you put
cuts to ensure that w is a single-valued function?
Problem 17.22: Cutting open a genus-2 surface. The Riemann surface for the function
y =
(z − a
1
)(z − a
2
)(z − a
3
)(z − a
4
)(z − a
5
)(z − a
6
)
has genus g = 2. Such a surface M is sketched in Figure 17.22, where the four inde-
pendent 1-cycles α
1,2
and β
1,2
that generate H
1
(M ) have been drawn so that they share
a common vertex.
(a) Realize the genus-2 surface as two copies of C ∪ {∞} cross-connected by three
square-root branch cuts. Sketch how the 1-cycles α
i
and β
i
, i = 1, 2 of Figure 17.22
appear when drawn on your thrice-cut plane.
(b) Cut the surface open along the four 1-cycles, and convince yourself that the resulting
surface is homeomorphic to the octagonal region appearing in Figure 17.23.
(c) Apply the direct method that gave us (13.79) to the octagonal region of part (b).
Hence show that for closed 1-forms a, b, on the surface we have
M
a ∧ b =
2
i=1
α
i
a
β
i
b −
β
i
a
α
i
b
.
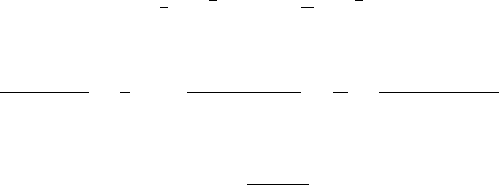
18
Applications of complex variables
In this chapter we will find uses for what we have learned of complex variables. The
applications will range from the elementary to the sophisticated.
18.1 Contour integration technology
The goal of contour integration technology is to evaluate ordinary, real-variable, definite
integrals. We have already met the basic tool, the residue theorem:
Theorem: Let f (z) be analytic within and on the boundary = ∂D of a simply connected
domain D, with the exception of a finite number of points at which the function has
poles. Then
F
f (z ) dz =
poles ∈ D
2πi (residue at pole).
18.1.1 Tricks of the trade
The effective application of the residue theorem is something of an art, but there are
useful classes of integrals which we can learn to recognize.
Rational trigonometric expressions
Integrals of the form
2π
0
F(cos θ , sin θ)dθ (18.1)
are dealt with by writing cos θ =
1
2
(z +z), sin θ =
1
2i
(z −z) and integrating around the
unit circle. For example, let a, b be real and b < a. Then
I =
2π
0
dθ
a + b cos θ
=
2
i
F
|z|=1
dz
bz
2
+ 2az + b
=
2
ib
F
dz
(z − α)(z − β)
. (18.2)
Since αβ = 1, only one pole is within the contour. This is at
α = (−a +
a
2
− b
2
)/b. (18.3)
666

18.1 Contour integration technology 667
The residue is
2
ib
1
α −β
=
1
i
1
√
a
2
− b
2
. (18.4)
Therefore, the integral is given by
I =
2π
√
a
2
− b
2
. (18.5)
These integrals are, of course, also do-able by the “t” substitution t = tan(θ/2), whence
sin θ =
2t
1 + t
2
, cos θ =
1 − t
2
1 + t
2
, dθ =
2dt
1 + t
2
, (18.6)
followed by a partial fraction decomposition. The labour is perhaps slightly less using
the contour method.
Rational functions
Integrals of the form
∞
−∞
R(x) dx, (18.7)
where R(x) is a rational function of x with the degree of the denominator exceeding
the degree of the numerator by two or more, may be evaluated by integrating around
a rectangle from −A to +A, A to A + iB, A + iB to −A + iB, and back down to −A.
Because the integrand decreases at least as fast as 1/|z|
2
as z becomes large, we see that
if we let A, B →∞, the contributions from the unwanted parts of the contour become
negligible. Thus
I = 2π i
Residues of poles in upper half-plane
. (18.8)
We could also use a rectangle in the lower half-plane with the result
I =−2πi
Residues of poles in lower half-plane
. (18.9)
This must give the same answer.
For example, let n be a positive integer and consider
I =
∞
−∞
dx
(1 + x
2
)
n
. (18.10)

668 18 Applications of complex variables
The integrand has an n-th order pole at z =±i. Suppose we close the contour in the
upper half-plane. The new contour encloses the pole at z =+i and we therefore need to
compute its residue. We set z −i = ζ and expand
1
(1 + z
2
)
n
=
1
[(i + ζ)
2
+ 1]
n
=
1
(2iζ)
n
1 −
iζ
2
−n
=
1
(2iζ)
n
1 + n
iζ
2
+
n(n + 1)
2!
iζ
2
2
+···
. (18.11)
The coefficient of ζ
−1
is
1
(2i)
n
n(n + 1) ···(2n − 2)
(n − 1)!
i
2
n−1
=
1
2
2n−1
i
(2n − 2)!
((n − 1)!)
2
. (18.12)
The integral is therefore
I =
π
2
2n−2
(2n − 2)!
((n − 1)!)
2
. (18.13)
These integrals can also be done by partial fractions.
18.1.2 Branch-cut integrals
Integrals of the form
I =
∞
0
x
α−1
R(x)dx, (18.14)
where R(x) is rational, can be evaluated by integration round a slotted circle (or “key-
hole”) contour (Figure 18.1). A little more work is required to extract the answer, though.
For example, consider
I =
∞
0
x
α−1
1 + x
dx,0< Re α<1. (18.15)
The restrictions on the range of α are necessary for the integral to converge at its upper
and lower limits.
We take to be a circle of radius centred at z = 0, with a slot indentation designed
to exclude the positive real axis, which we take as the branch cut of z
α−1
, and a small
circle of radius about the origin. The branch of the fractional power is defined by
setting
z
α−1
= exp[(α − 1)(ln |z|+iθ)], (18.16)
18.1 Contour integration technology 669
y
x
–1
Figure 18.1 A slotted circle contour of outer radius and inner radius .
where we will take θ to be zero immediately above the real axis, and 2π immediately
below it. With this definition the residue at the pole at z =−1ise
iπ(α−1)
. The residue
theorem therefore tells us that
F
z
α−1
1 + z
dz = 2π ie
πi(α−1)
. (18.17)
The integral decomposes as
F
z
α−1
1 + z
dz =
F
|z|=
z
α−1
1 + z
dz + (1 − e
2πi(α−1)
)
x
α−1
1 + x
dx −
F
|z|=
z
α−1
1 + z
dz.
(18.18)
As we send off to infinity we can ignore the “1” in the denominator compared to the
z, and so estimate
!
!
!
!
F
|z|=
z
α−1
1 + z
dz
!
!
!
!
→
!
!
!
!
F
|z|=
z
α−2
dz
!
!
!
!
≤ 2π ×
Re (α)−2
. (18.19)
This tends to zero provided that Re α<1. Similarly, provided 0 < Re α, the integral
around the small circle about the origin tends to zero with . Thus
−e
πiα
2πi =
1 − e
2πi(α−1)
I. (18.20)
We conclude that
I =
2πi
(e
πiα
− e
−πiα
)
=
π
sin πα
. (18.21)
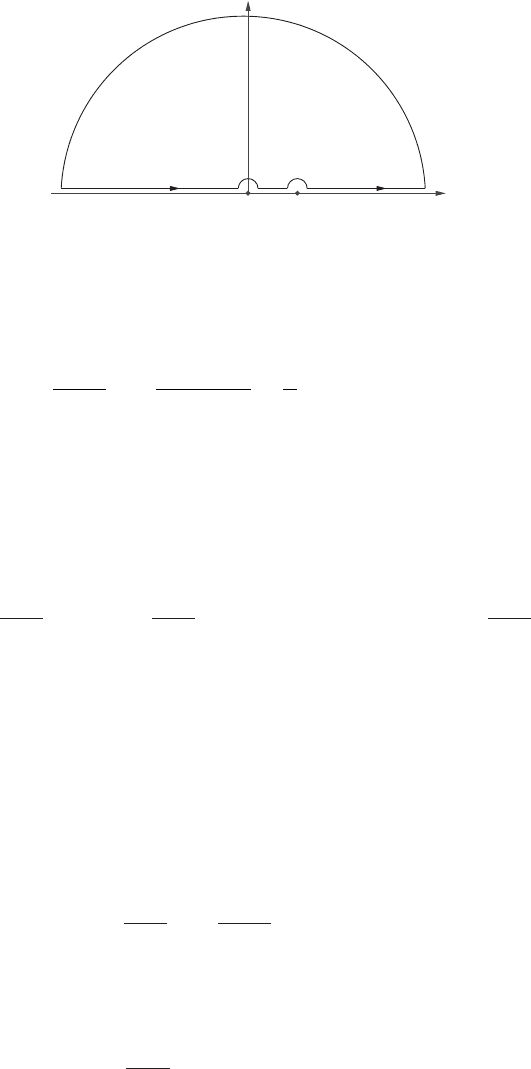
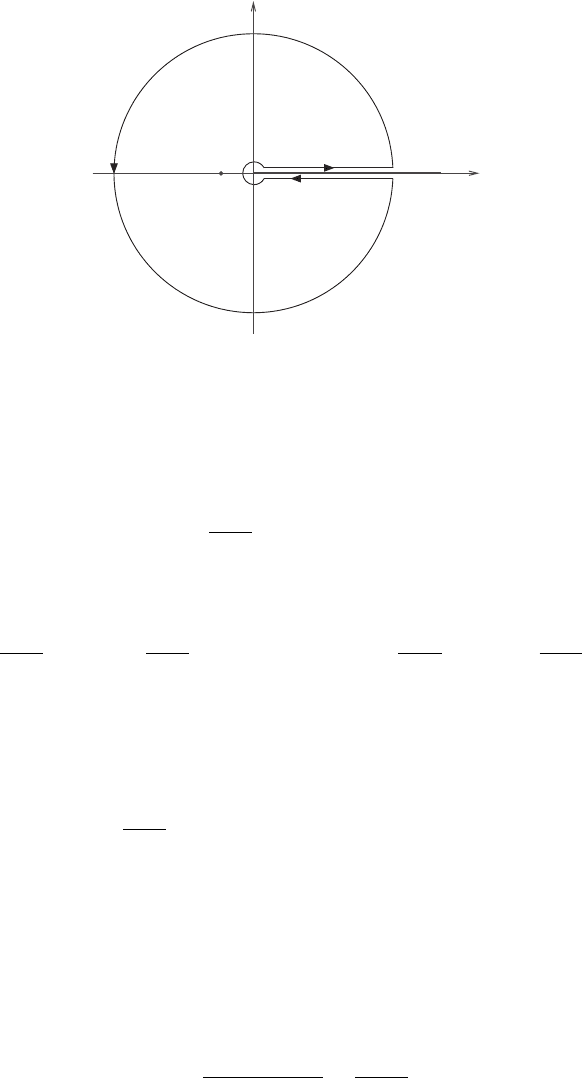
670 18 Applications of complex variables
x
y
1
Figure 18.2 The contour
1
.
Exercise 18.1: Using the slotted circle contour, show that
I =
∞
0
x
p−1
1 + x
2
dx =
π
2 sin(πp/2)
=
π
2
cosec (πp/2),0< p < 2.
Exercise 18.2: Integrate z
a−1
/(z − 1) around a contour
1
consisting of a semicircle
in the upper half-plane together with the real axis indented at z = 0 and z = 1 (see
Figure 18.2)toget
0 =
F
z
a−1
z − 1
dz = P
∞
0
x
a−1
x − 1
dx − iπ + (cos π a + i sin π a)
∞
0
x
a−1
x + 1
dx.
As usual, the symbol P in front of the integral sign denotes a principal-part integral,
meaning that we must omit an infinitesimal segment of the contour symmetrically dis-
posed about the pole at z = 1. The term −iπ comes from integrating around the small
semicircle about this point. We get −1/2 of the residue because we have only a half-
circle, and that traversed in the “wrong” direction. Warning: this fractional residue
result is only true when we indent to avoid a simple pole – i.e. one that is of order one.
Now take real and imaginary parts and deduce that
∞
0
x
a−1
1 + x
dx =
π
sin πα
,0< Re a < 1,
and
P
∞
0
x
a−1
1 − x
dx = π cot πa,0< Re a < 1.
18.1 Contour integration technology 671
18.1.3 Jordan’s lemma
We often need to evaluate Fourier integrals
I(k) =
∞
−∞
e
ikx
R(x) dx (18.22)
with R(x) a rational function. For example, the Green function for the operator −∂
2
x
+m
2
is given by
G(x) =
∞
−∞
dk
2π
e
ikx
k
2
+ m
2
. (18.23)
Suppose x ∈ R and x > 0. Then, in contrast to the analogous integral without the
exponential function, we have no flexibility in closing the contour in the upper or lower
half-plane. The function e
ikx
grows without limit as we head south in the lower half-
plane, but decays rapidly in the upper half-plane. This means that we may close the
contour without changing the value of the integral by adding a large upper-half-plane
semicircle (Figure 18.3).
The modified contour encloses a pole at k = im, and this has residue i/(2m)e
−mx
. Thus
G(x) =
1
2m
e
−mx
, x > 0. (18.24)
For x < 0, the situation is reversed, and we must close in the lower half-plane. The
residue of the pole at k =−im is −i/(2m)e
mx
, but the minus sign is cancelled because
the contour goes the “wrong way” (clockwise). Thus
G(x) =
1
2m
e
+mx
, x < 0. (18.25)
R
k
im
–im
Figure 18.3 Closing the contour in the upper half-plane.

672 18 Applications of complex variables
We can combine the two results as
G(x) =
1
2m
e
−m|x|
. (18.26)
The formal proof that the added semicircles make no contribution to the integral when
their radius becomes large is known as Jordan’s lemma:
Lemma: Let be a semicircle, centred at the origin, and of radius R. Suppose that
(i) f (z) is meromorphic in the upper half-plane;
(ii) f (z) tends uniformly to zero as |z|→∞for 0 < arg z <π;
(iii) the number λ is real and positive.
Then
e
iλz
f (z ) dz → 0, as R →∞. (18.27)
To establish this, we assume that R is large enough that |f | <on the contour, and
make a simple estimate
!
!
!
!
e
iλz
f (z ) dz
!
!
!
!
< 2R
π/2
0
e
−λR sin θ
dθ
< 2R
π/2
0
e
−2λRθ/π
dθ
=
π
λ
(1 − e
−λR
)<
π
λ
. (18.28)
In the second inequality we have used the fact that (sin θ )/θ ≥ 2/π for angles in the
range 0 <θ <π/2. Since can be made as small as we like, the lemma follows.
Example: Evaluate
I(α) =
∞
−∞
sin(αx)
x
dx. (18.29)
We have
I(α) = Im
∞
−∞
exp iαz
z
dz
. (18.30)
If we take α>0, we can close in the upper half-plane, but our contour must exclude the
pole at z = 0. Therefore
0 =
|z|=R
exp iαz
z
dz −
|z|=
exp iαz
z
dz +
−
−R
exp iαx
x
dx +
R
exp iαx
x
dx.
(18.31)

18.1 Contour integration technology 673
As R →∞, we can ignore the big semicircle, the rest, after letting → 0, gives
0 =−iπ + P
∞
−∞
e
iαx
x
dx. (18.32)
Again, the symbol P denotes a principal-part integral. The −iπ comes from the small
semicircle. We get −1/2 of the residue because we have only a half circle, and that
traversed in the “wrong” direction. (Remember that this fractional residue result is only
true when we indent to avoid a simple pole – i.e one that is of order one.)
Reading off the real and imaginary parts, we conclude that
∞
−∞
sin αx
x
dx = π, P
∞
−∞
cos αx
x
dx = 0, α>0. (18.33)
No “P” is needed in the sine integral, as the integrand is finite at x = 0.
If we relax the condition that α>0 and take into account that sine is an odd function
of its argument, we have
∞
−∞
sin αx
x
dx = π sgn α. (18.34)
This identity is called Dirichlet’s discontinuous integral.
We can interpret Dirichlet’s integral as giving the Fourier transform of the principal-
part distribution P(1/x) as
P
∞
−∞
e
iωx
x
dx = iπ sgn ω. (18.35)
This will be of use later in the chapter.
Example: We will evaluate the integral
F
C
e
iz
z
a−1
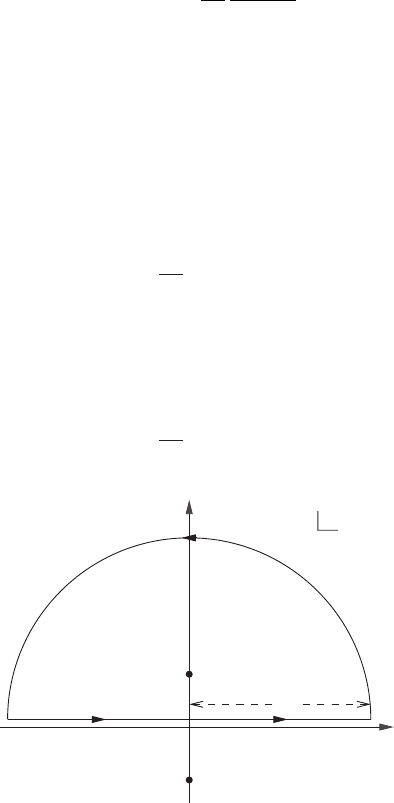
dz (18.36)
about the first-quadrant contour shown in Figure 18.4. Observe that when 0 < a < 1
neither the large nor the small arc makes a contribution, and that there are no poles.
Hence, we deduce that
0 =
∞
0
e
ix
x
a−1
dx − i
∞
0
e
−y
y
a−1
e
(a−1)
π
2
i
dy ,0< a < 1. (18.37)
Taking real and imaginary parts, we find
∞
0
x
a−1
cos xdx = (a) cos
π
2
a
,0< a < 1,
∞
0
x
a−1
sin xdx = (a) sin
π
2
a
,0< a < 1, (18.38)

674 18 Applications of complex variables
x
y
Figure 18.4 Quadrant contour.
where
(a) =
∞
0
y
a−1
e
−y
dy (18.39)
is the Euler Gamma function.
Example: Fresnel integrals. Integrals of the form
C(t) =
t
0
cos(πx
2
/2) dx, (18.40)
S(t) =
t
0
sin(πx
2
/2) dx, (18.41)
occur in the theory of diffraction and are called Fresnel integrals after Augustin Fresnel.
They are naturally combined as
C(t) + iS(t) =
t
0
e
iπ x
2
/2
dx. (18.42)
The limit as t →∞exists and is finite. Even though the integrand does not tend to zero
at infinity, its rapid oscillation for large x is just sufficient to ensure convergence.
1
1
We can exhibit this convergence by setting x
2
= s and then integrating by parts to get
t
0
e
iπ x
2
/2
dx =
1
2
1
0
e
iπ s/2
ds
s
1/2
+
%
e
iπ s/2
πis
1/2
&
t
2
1
+
1
2πi
t
2
1
e
iπ s/2
ds
s
3/2
.
The right-hand side is now manifestly convergent as t →∞.
