Stone M., Goldbart P. Mathematics for Physics: A Guided Tour for Graduate Students
Подождите немного. Документ загружается.


18.2 The Schwarz reflection principle 685
Exercise 18.4: Let
;
f (ω) =
∞
−∞
e
iωt
f (t) dt denote the Fourier transform of f (t). Use the
formula (18.35) for the Fourier transform of P(1/t), combined with the convolution the-
orem for Fourier transforms, to show that the Fourier transform of the Hilbert transform
of f (t) is
(Hf )(ω) = i sgn(ω)
;
f (ω).
Deduce that the analytic signal is derived from the original real signal by suppressing all
positive frequency components (those proportional to e
−iωt
with ω>0) and multiplying
the remaining negative-frequency amplitudes by 2.
Exercise 18.5: Suppose that ϕ
1
(x) and ϕ
2
(x) are real functions with finite L
2
(R) norms.
(a) Use the Fourier transform result from the previous exercise to show that
ϕ
1
, ϕ
2
=Hϕ
1
, Hϕ
2
.
Thus, H is a unitary transformation from L
2
(R) → L
2
(R).
(b) Use the fact that H
2
=−I to deduce that
Hϕ
1
, ϕ
2
=−ϕ
1
, Hϕ
2
and so H
†
=−H.
(c) Conclude from part (b) that
∞
−∞
ϕ
1
(x)
P
∞
−∞
ϕ
2
(y )
x − y
dy
dx =
∞
−∞
ϕ
2
(y )
P
∞
−∞
ϕ
1
(x)
x − y
dx
dy ,
i.e. for L
2
(R) functions, it is legitimate to interchange the order of “P” integration
with ordinary integration.
d) By replacing ϕ
1
(x) by a constant, and ϕ
2
(x) by the Hilbert transform of a function
f with
fdx= 0, show that it is not always safe to interchange the order of “P”
integration with ordinary integration.
Exercise 18.6: Suppose that we are given real functions u
1
(x) and u
2
(x) and substitute
their Hilbert transforms v
1
= Hu
1
, v
2
= Hu
2
into (18.78) to construct analytic functions
f
1
(z) and f
2
(z) that are analytic in the upper half-plane and tend to zero at infinity there.
Then, as we approach the real axis from above, the product f
1
(z)f
2
(z) = F(z) has
boundary value
F
R
(x + i) + iF
I
(x + i) = (u
1
u
2
− v
1
v
2
) + i(u
1
v
2
+ u
2
v
1
).
By assuming that F(z) satisfies the conditions for (18.77) to be applicable to this boundary
value, deduce that
H
(
(Hu
1
)u
2
) + H ((Hu
2
)u
1
)
− (Hu
1
)(Hu
2
) =−u
1
u
2
. ()

686 18 Applications of complex variables
This result
5
sometimes appears in the physics literature
6
in the guise of the distributional
identity
P
x − y
P
y − z
+
P
y − z
P
z − x
+
P
z − x
P
x − y
=−π
2
δ(x −y)δ(x − z),
where P/(x −y) denotes the principal-part distribution P
1/(x − y)
. This attractively
symmetric form conceals the fact that x is being kept fixed, while y and z are being
integrated over in specific orders. As the next exercise shows, were we to freely rearrange
the integration order we could use the identity
1
x − y
1
y − z
+
1
y − z
1
z − x
+
1
z − x
1
x − y
= 0 x, y, z distinct
to wrongly conclude that the right-hand side of () is zero.
Problem 18.7: Show that the identity () from Exercise 18.6 can be written as
∞
−∞
∞
−∞
u
1
(y )u
2
(z)
(z − y)(y − x)
dz
dy
=
∞
−∞
∞
−∞
u
1
(y )u
2
(z)
(z − y)(y − x)
dy
dz − π
2
u
1
(x)u
2
(x),
principal-part integrals being understood where necessary. This is a special case of a
more general change-of-integration-order formula
∞
−∞
∞
−∞
f (x, y, z)
(z − y)(y − x)
dz
dy
=
∞
−∞
∞
−∞
f (x, y, z)
(z − y)(y − x)
dy
dz − π
2
f (x, x, x),
which was first obtained by G. H. Hardy in 1908. Hardy’s result is often referred to as
the Poincaré–Bertrand theorem.
Verify Hardy’s formula for the particular case where x is zero and f (0, y, z) is unity
when both y and z lie within the interval [−a, a] but zero elsewhere. You will need to
show that
∞
0
ln
a − x
a + x
2
dx
x
=−π
2
sgn(a).
(Hint: observe that the integrand is singular at x =|a|. Explain why it is legitimate to
evaluate the improper integral by expanding the logarithms as a power series in x or x
−1
,
and then integrating term-by-term.)
5
A sufficient condition for its validity is that u
1
∈ L
p
1
(R), u
2
∈ L
p
2
(R), where p
1
and p
2
are greater than
unity and 1/p
1
+ 1/p
2
< 1. See F. G. Tricomi, Quart. J. Math. (Oxford), series 2, 2 (1951) 199.
6
For example, in R. Jackiw, A. Strominger, Phys. Lett., 99B (1981) 133.

18.3 Partial-fraction and product expansions 687
Exercise 18.8: Use the licit interchange of “P” integration with ordinary integration to
show that
∞
−∞
ϕ(x)
P
∞
−∞
ϕ(y)
x − y
dy
2
dx =
π
2
3
∞
−∞
ϕ
3
(x) dx.
Exercise 18.9: Let f (z ) be analytic within the unit circle, and let u(θ) and v(θ ) be the
boundary values of its real and imaginary parts, respectively, at z = e
iθ
. Use Plemelj to
show that
u(θ) =−
1
2π
P
2π
0
v(θ
) cot
θ − θ
2
dθ
+
1
2π
2π
0
u(θ
) dθ
,
v(θ) =
1
2π
P
2π
0
u(θ
) cot
θ − θ
2
dθ
+
1
2π
2π
0
v(θ
) dθ
.
18.3 Partial-fraction and product expansions
In this section we will study other useful representations of functions which devolve
from their analyticity properties.
18.3.1 Mittag-Leffler partial-fraction expansion
Let f (z) be a meromorphic function with poles (perhaps infinitely many) at z = z
j
,
(j = 1, 2, 3, ...), where |z
1
| < |z
2
| < ...Let
n
be a contour enclosing the first n poles.
Suppose further (for ease of description) that the poles are simple and have residue r
n
.
Then, for z inside
n
, we have
1
2πi
F
n
f (z
)
z
− z
dz
= f (z) +
n
j=1
r
j
z
j
− z
. (18.81)
We often want to apply this formula to trigonometric functions whose periodicity means
that they do not tend to zero at infinity. We therefore employ the same strategy that we
used for dispersion relations: we subtract f (0) from f (z) to find
f (z ) − f (0) =
z
2πi
F
n
f (z
)
z
(z
− z)
dz
+
n
j=1
r
j
1
z − z
j
+
1
z
j
. (18.82)
If we now assume that f (z) is uniformly bounded on the
n
– this meaning that |f (z)| < A
on
n
, with the same constant A working for all n – then the integral tends to zero as n
becomes large, yielding the partial-fraction, or Mittag-Leffler, decomposition
f (z ) = f (0) +
∞
j=1
r
j
1
z − z
j
+
1
z
j
. (18.83)

688 18 Applications of complex variables
Example: Consider cosec z. The residues of 1/(sin z) at its poles at z = nπ are r
n
=
(−1)
n
. We can take the
n
to be squares with corners (n +1/2)(±1 ±i)π. A bit of effort
shows that cosec is uniformly bounded on them. To use the formula as given, we first
need to subtract the pole at z = 0, then
cosec z −
1
z
=
∞
n=−∞
(−1)
n
1
z − nπ
+
1
nπ
. (18.84)
The prime on the summation symbol indicates that we are to omit the n = 0 term. The
positive and negative n series converge separately, so we can add them, and write the
more compact expression
cosec z =
1
z
+ 2z
∞
n=1
(−1)
n
1
z
2
− n
2
π
2
. (18.85)
Example: A similar method applied to cot z yields
cot z =
1
z
+
∞
n=−∞
1
z − nπ
+
1
nπ
. (18.86)
We can pair terms together to write this as
cot z =
1
z
+
∞
n=1
1
z − nπ
+
1
z + nπ
,
=
1
z
+
∞
n=1
2z
z
2
− n
2
π
2
(18.87)
or
cot z = lim
N →∞
N
n=−N
1
z − nπ
. (18.88)
In the last formula it is important that the upper and lower limits of summation be the
same. Neither the sum over positive n nor the sum over negative n converges separately.
By taking asymmetric upper and lower limits we could therefore obtain any desired
number as the limit of the sum.
Exercise 18.10: Use Mittag-Leffler to show that
cosec
2
z =
∞
n=−∞
1
(z + nπ)
2
.
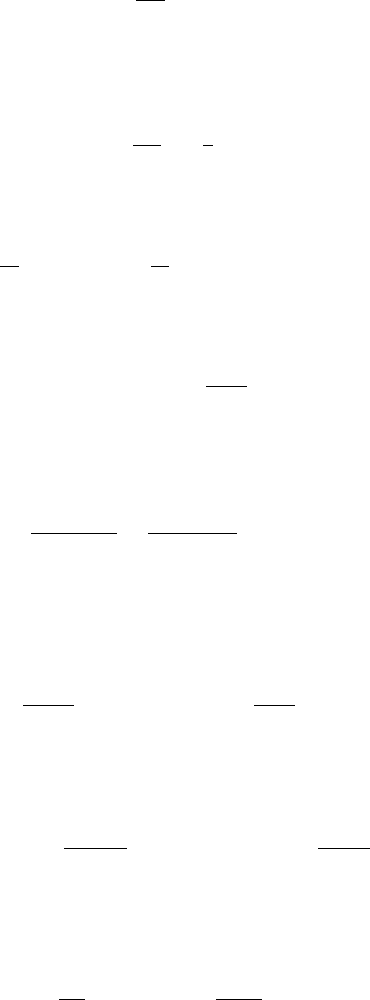
18.3 Partial-fraction and product expansions 689
Now use this infinite series to give a one-line proof of the trigonometric identity
N −1
m=0
cosec
2
z +
mπ
N
= N
2
cosec
2
(Nz).
(Is there a comparably easy elementary derivation of this finite sum?) Take a limit to
conclude that
N −1
m=1
cosec
2
mπ
N
=
1
3
(N
2
− 1).
Exercise 18.11: From the partial fraction expansion for cot z, deduce that
d
dz
ln[(sin z )/z]=
d
dz
∞
n=1
ln(z
2
− n
2
π
2
).
Integrate this along a suitable path from z = 0, and so conclude that
sin z = z
∞
9
n=1
1 −
z
2
n
2
π
2
.
Exercise 18.12: By differentiating the partial fraction expansion for cot z, show that, for
k an integer ≥ 1, and Im z > 0, we have
∞
n=−∞
1
(z + n)
k+1
=
(−2πi)
k+1
k!
∞
n=1
n
k
e
2πinz
.
This is called Lipshitz’ formula.
Exercise 18.13: The Bernoulli numbers are defined by
x
e
x
− 1
= 1 + B
1
x +
∞
k=1
B
2k
x
2k
(2k)!
.
The first few are B
1
=−1/2, B
2
= 1/6, B
4
=−1/30. Except for B
1
, the B
n
are zero
for n odd. Show that
x cot x = ix +
2ix
e
2ix
− 1
= 1 −
∞
k=1
(−1)
k+1
B
2k
2
2k
x
2k
(2k)!
.
By expanding 1/(x
2
−n
2
π
2
) as a power series in x and comparing coefficients, deduce
that, for positive integer k,
∞
n=1
1
n
2k
= (−1)
k+1
π
2k
2
2k−1
(2k)!
B
2k
.
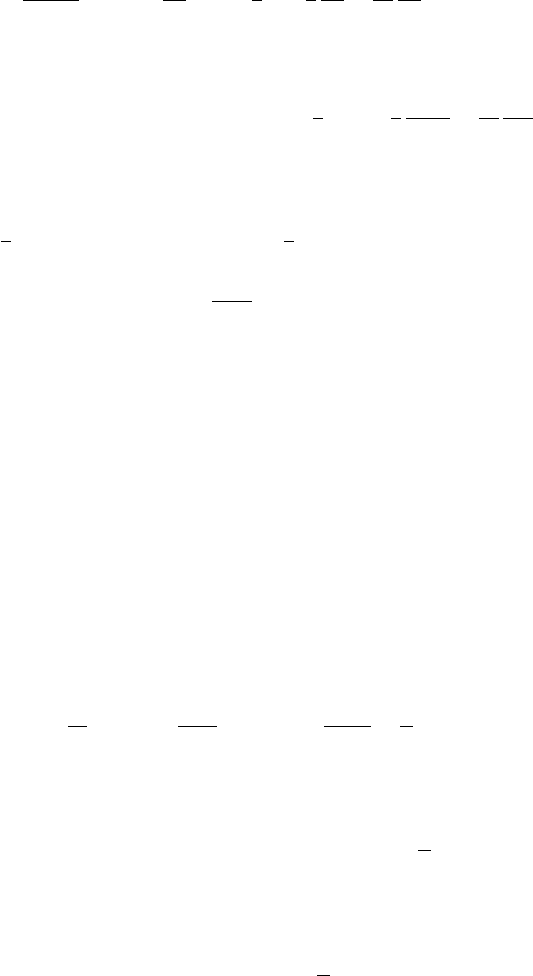
690 18 Applications of complex variables
Exercise 18.14: Euler–Maclaurin sum formula. Let f (x) be a real analytic function. Use
the formal expansion
D
e
D
− 1
=
k
B
k
D
k
k!
= 1 −
1
2
D +
1
6
D
2
2!
−
1
30
D
4
4!
+···,
with D interpreted as d/dx, to obtain
(−f
(x) − f
(x + 1) − f
(x + 2) +···) = f (x) −
1
2
f
(x) +
1
6
f
(x)
2!
−
1
30
f
(4)
4!
+···.
By integrating this formula from 0 to M , where M is an integer, motivate the Euler–
Maclaurin sum formula:
1
2
f (0) + f (1) +···+f (M − 1) +
1
2
f (M )
=
M
0
f (x) dx +
∞
k=1
B
2k
(2k)!
(f
(2k−1)
(M ) − f
(2k−1)
(0)).
The left-hand side is the trapezium rule approximation to the integral on the right-hand
side. This derivation gives no insight into whether the infinite-sum correction to the
trapezium rule converges (usually it does not), or what the error will be if we truncate
the sum after a finite number of terms. When f (x) is a polynomial, however, only a finite
number of derivatives f
(2k−1)
are non-zero, and the result is exact.
18.3.2 Infinite product expansions
We can play a variant of the Mittag-Leffler game with suitable entire functions g(z) and
derive for them a representation as an infinite product. Suppose that g(z) has simple
zeros at z
i
. Then (ln g)
= g
(z)/g(z) is meromorphic with poles at z
i
, all with unit
residues. Assuming that it satisfies the uniform boundedness condition, we now use
Mittag-Leffler to write
d
dz
ln g(z) =
g
(z)
g(z)
!
!
!
!
z=0
+
∞
j=1
1
z − z
j
+
1
z
j
. (18.89)
Integrating up we have
ln g(z) = ln g(0) + cz +
∞
j=1
ln(1 − z/z
j
) +
z
z
j
, (18.90)
where c = g
(0)/g(0). We now re-exponentiate to get
g(z) = g(0)e
cz
∞
9
j=1
1 −
z
z
j
e
z/z
j
. (18.91)

18.3 Partial-fraction and product expansions 691
Example: Let g(z) = sin z/z. Then g(0) = 1, while the constant c, which is the
logarithmic derivative of g at z = 0, is zero, and
sin z
z
=
∞
9
n=1
1 −
z
nπ
e
z/nπ
1 +
z
nπ
e
−z/nπ
. (18.92)
Thus
sin z = z
∞
9
n=1
1 −
z
2
n
2
π
2
. (18.93)
Convergence of infinite products
We have derived several infinite problem formulæ without discussing the issue of their
convergence. For products of terms of the form (1 +a
n
) with positive a
n
we can reduce
the question of convergence to that of
,
∞
n=1
a
n
.
To see why this is so, let
p
N
=
N
9
n=1
(1 + a
n
), a
n
> 0. (18.94)
Then we have the inequalities
1 +
N
n=1
a
n
< p
N
< exp
N
n=1
a
n
. (18.95)
The infinite sum and product therefore converge or diverge together. If
P =
∞
9
n=1
(1 +|a
n
|) (18.96)
converges, we say that
p =
∞
9
n=1
(1 + a
n
) (18.97)
converges absolutely. As with infinite sums, absolute convergence implies convergence,
but not vice versa. Unlike infinite sums, however, an infinite product containing negative
a
n
can diverge to zero.If(1 +a
n
)>0 then
J
(1 +a
n
) converges if
,
ln(1 +a
n
) does,
and we will say that
J
(1 + a
n
) diverges to zero if
,
ln(1 + a
n
) diverges to −∞.

692 18 Applications of complex variables
Exercise 18.15: Show that
N
9
n=1
1 +
1
n
= N + 1,
N
9
n=2
1 −
1
n
=
1
N
.
From these deduce that
∞
9
n=2
1 −
1
n
2
=
1
2
.
Exercise 18.16: For |z| < 1, show that
∞
9
n=0
1 + z
2
n
=
1
1 − z
.
(Hint: think binary.)
Exercise 18.17: For |z | < 1, show that
∞
9
n=1
(1 + z
n
) =
∞
9
n=1
1
1 − z
2n−1
.
(Hint: 1 − x
2n
= (1 − x
n
)(1 + x
n
).)
18.4 Wiener–Hopf equations II
The theory of Hilbert transforms has shown us some of the consequences of functions
being analytic in the upper or lower half-plane. Another application of these ideas is to
Wiener–Hopf equations. Although we have discussed Wiener–Hopf integral equations
in Chapter 9, it is only now that we possess the tools to appreciate the general theory.
We begin, however, with the slightly simpler Wiener–Hopf sum equations, which are
their discrete analogue. Here, analyticity in the upper or lower half-plane is replaced by
analyticity within or without the unit circle.
18.4.1 Wiener–Hopf sum equations
Consider the infinite system of equations
y
n
=
∞
m=−∞
a
n−m
x
m
, −∞ < n < ∞ (18.98)
where we are given the y
n
and are seeking the x
n
.
18.4 Wiener–Hopf equations II 693
If the a
n
, y
n
are the Fourier coefficients of smooth complex-valued functions
A(θ) =
∞
n=−∞
a
n
e
inθ
,
Y (θ) =
∞
n=−∞
y
n
e
inθ
, (18.99)
then the system of equations is, in principle at least, easy to solve. We introduce the
function
X (θ) =
∞
n=−∞
x
n
e
inθ
, (18.100)
and (18.98) becomes
Y (θ) = A(θ )X (θ ). (18.101)
From this, the desired x
n
may be read off as the Fourier expansion coefficients of
Y (θ)/A(θ ). We see that A(θ) must be nowhere zero or else the operator A represented
by the infinite matrix a
n−m
will not be invertible. This technique is a discrete version of
the Fourier transform method for solving the integral equation
y (s) =
∞
−∞
A(s − t)x(t) dt, −∞ < s < ∞. (18.102)
The connection with complex analysis is made by regarding A(θ), X (θ ), Y (θ) as being
functions on the unit circle in the z plane. If they are smooth enough we can extend their
definition to an annulus about the unit circle, so that
A(z) =
∞
n=−∞
a
n
z
n
,
X (z) =
∞
n=−∞
x
n
z
n
,
Y (z) =
∞
n=−∞
y
n
z
n
. (18.103)
The x
n
may now be read off as the Laurent expansion coefficients of Y (z)/A(z).
The discrete analogue of the Wiener–Hopf integral equation
y (s) =
∞
0
A(s − t)x(t) dt,0≤ s < ∞ (18.104)
694 18 Applications of complex variables
is the Wiener–Hopf sum equation
y
n
=
∞
m=0
a
n−m
x
m
,0≤ n < ∞. (18.105)
This requires a more sophisticated approach. If you look back at our earlier discussion
of Wiener–Hopf integral equations in Chapter 9, you will see that the trick for solving
them is to extend the definition y(s) to negative s (analogously, the y
n
to negative n) and
find these values at the same time as we find x(s) for positive s (analogously, the x
n
for
positive n).
We proceed by introducing the same functions A(z), X (z), Y (z) as before, but now
keep careful track of whether their power-series expansions contain positive or negative
powers of z. In doing so, we will discover that the Fredholm alternative governing the
existence and uniqueness of the solutions will depend on the winding number N =
n(,0) where is the image of the unit circle under the map z (→ A(z) – in other words,
on how many times A(z) wraps around the origin as z goes once round the unit circle.
Suppose that A(z) is smooth enough that it is analytic in an annulus including the unit
circle, and that we can factorize A(z) so that
A(z) = λq
+
(z)z
N
[q
−
(z)]
−1
, (18.106)
where
q
+
(z) = 1 +
∞
n=1
q
+
n
z
n
,
q
−
(z) = 1 +
∞
n=1
q
−
−n
z
−n
. (18.107)
Here we demand that q
+
(z) be analytic and non-zero for |z| < 1 + , and that q
−
(z) be
analytic and non-zero for |1/z| < 1 + . These no-pole, no-zero, conditions ensure, via
the principle of the argument, that the winding numbers of q
±
(z) about the origin are
zero, and so all the winding of A(z) is accounted for by the N -fold winding of the z
N
factor. The non-zero condition also ensures that the reciprocals [q
±
(z)]
−1
have the same
class of expansions (i.e. in positive or negative powers of z only) as the direct functions.
We now introduce the notation [F(z)]
+
and [F(z)]
−
, meaning that we expand F(z)
as a Laurent series and retain only the positive powers of z (including z
0
), or only the
negative powers (starting from z
−1
), respectively. Thus F(z) =[F(z)]
+
+[F(z)]
−
.We
will write Y
±
(z) =[Y (z)]
±
, and similarly for X (z). We can therefore rewrite (18.105)
in the form
λz
N
q
+
(z)X
+
=[Y
+
(z) + Y
−
(z)]q
−
(z). (18.108)
