Stone M., Goldbart P. Mathematics for Physics: A Guided Tour for Graduate Students

Подождите немного. Документ загружается.

18.1 Contour integration technology 675

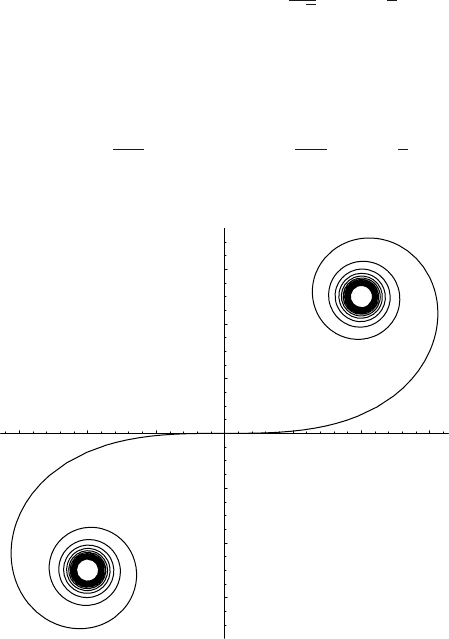
As t varies, the complex function C(t) + iS(t) traces out the Cornu spiral, named

after Marie Alfred Cornu, a nineteenth-century French optical physicist.

We can evaluate the limiting value

C(∞) + iS(∞) =



∞

iπ x

dx (18.43)

by deforming the contour off the real axis and onto a line of length L running into the

first quadrant at 45

◦

, this being the direction of most rapid decrease of the integrand

(Figure 18.6).

A circular arc returns the contour to the axis whence it continues to ∞, but an estimate

similar to that in Jordan’s lemma shows that the arc and the subsequent segment on the

real axis make a negligible contribution when L is large. To evaluate the integral on the

radial line we set z = e

iπ/4

s, and so



iπ/4

∞

iπ z

dz = e

iπ/4



∞

−πs

ds =

√

iπ/4

(1 + i). (18.44)

Figure 18.5 shows how C(t) +iS(t) orbits the limiting point 0.5+0.5i and slowly spirals

in towards it. Taking real and imaginary parts we have



∞

cos



πx



dx =



∞

sin



πx



dx =

. (18.45)

–0.75 –0.5 –0.25 0.25 0.5 0.75

–0.6

–0.4

–0.2

0.2

0.4

0.6

Figure 18.5 The Cornu spiral C(t) + iS(t) for t in the range −8 < t < 8. The spiral in the first

quadrant corresponds to positive values of t.

676 18 Applications of complex variables

Figure 18.6 Fresnel contour.

18.2 The Schwarz reflection principle

Theorem (Schwarz): Let f (z) be analytic in a domain D where ∂D includes a segment

of the real axis. Assume that f (z) is real when z is real. Then there is a unique analytic

continuation of f into the region

D (the mirror image of D in the real axis; see Figure 18.7)

given by

g(z) =

⎧

⎨

⎩

f (z ), z ∈ D,

either, z ∈ R.

(18.46)

The proof invokes Morera’s theorem to show analyticity, and then appeals to the

uniqueness of analytic continuations. Begin by looking at a closed contour lying

only in

f (z ) dz, (18.47)

where C ={

η(t)} is the image of C ={η(t)}⊂D under reflection in the real axis. We

can rewrite this as

f (z ) dz =

f (η)

d ¯η

dt =

f (η)

dη

dt =

f (η) dz = 0. (18.48)

At the last step we have used Cauchy and the analyticity of f in D. Morera’s theorem

therefore confirms that g(z) is analytic in

D. By breaking a general contour up into parts

in D and parts in

D, we can similarly show that g(z) is analytic in D ∪ D.

The important corollary is that if f (z) is analytic, and real on some segment of the real

axis, but has a cut along some other part of the real axis, then f (x + i) =

f (x − i) as

we go over the cut. The discontinuity disc f is therefore 2Im f (x + i).

Suppose f (z) is real on the negative real axis, and goes to zero as |z|→∞. Then

applying Cauchy to the contour  depicted in Figure 18.8.

18.2 The Schwarz reflection principle 677

Figure 18.7 The domain D and its mirror image



Figure 18.8 The contour  for the dispersion relation.

we find

f (ζ ) =



∞

Im f (x + i)

x − ζ

dx, (18.49)

for ζ within the contour. This is an example of a dispersion relation. The name comes

from the prototypical application of this technology to optical dispersion, i.e. the variation

of the refractive index with frequency.

If f (z) does not tend to zero at infinity then we cannot ignore the contribution to

Cauchy’s formula from the large circle. We can, however, still write

f (ζ ) =

2πi



f (z )

z − ζ

dz, (18.50)

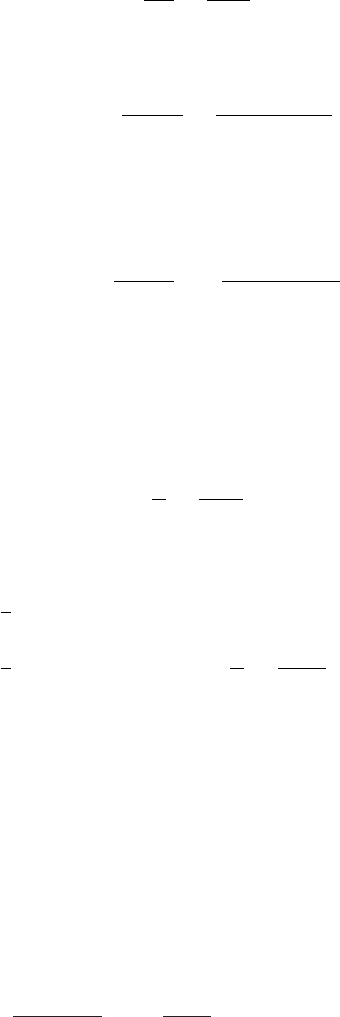
678 18 Applications of complex variables

and

f (b) =

2πi



f (z )

z − b

dz, (18.51)

for some convenient point b within the contour. We then subtract to get

f (ζ ) = f (b) +

(ζ − b)

2πi





f (z )

(z − b)(z − ζ)

dz. (18.52)

Because of the extra power of z downstairs in the integrand, we only need f to be

bounded at infinity for the contribution of the large circle to tend to zero. If this is the

case, we have

f (ζ ) = f (b) +

(ζ − b)



∞

Im f (x + i)

(x − b)(x − ζ)

dx. (18.53)

This is called a once-subtracted dispersion relation.

The dispersion relations derived above apply when ζ lies within the contour. In physics

applications we often need f (ζ ) for ζ real and positive. What happens as ζ approaches

the axis, and we attempt to divide by zero in such an integral, is summarized by the

Plemelj formulæ:Iff (ζ ) is defined by

f (ζ ) =





ρ(z)

z − ζ

dz, (18.54)

where  has a segment lying on the real axis, then, if x lies in this segment,

(f (x + i) − f (x −i)) = iρ(x)

(f (x + i) + f (x −i)) =





ρ(x



)



− x



. (18.55)

As always, the “P” means that we are to delete an infinitesimal segment of the contour

lying symmetrically about the pole.

The Plemelj formulæ hold under relatively mild conditions on the function ρ(x).We

won’t try to give a general proof, but in the case that ρ is analytic the result is easy

to understand: we can push the contour out of the way and let ζ → x on the real axis

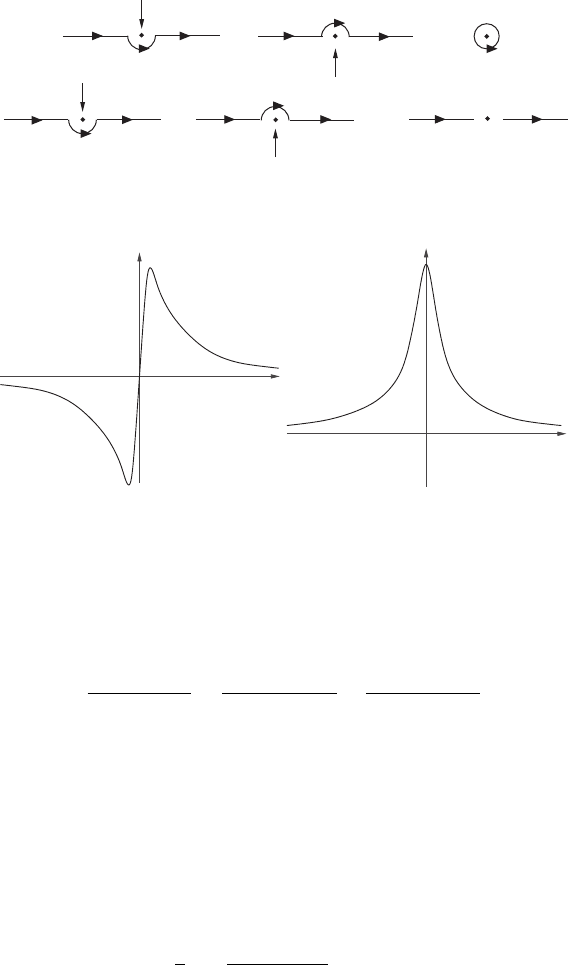
from either above or below. In that case the drawing in Figure 18.9 shows how the sum

of these two limits gives the principal-part integral and how their difference gives an

integral round a small circle, and hence the residue ρ(x).

The Plemelj equations usually appear in physics papers as the “i” cabala (see

Figure 18.10)



− x ± i

= P





− x



∓ iπδ(x



− x). (18.56)

18.2 The Schwarz reflection principle 679

= 2

–

Figure 18.9 Origin of the Plemelj formulae.

Im f

Re f

x– x

x–

Figure 18.10 Sketch of the real and imaginary parts of f (x



) = 1/(x



− x − i).

A limit  → 0 is always to be understood in this formula.

We can also appreciate the origin of the i rule by examining the following identity:



− (x ± i)

x − x



− x)

+ 

i



− x)

+ 

. (18.57)

The first term is a symmetrically cut-off version of 1/(x



−x) and provides the principal-

part integral. The second term sharpens and tends to the delta function ±iπδ(x



− x)

as  → 0.

Exercise 18.3: The Legendre function of the second kind, Q

(z), may be defined for

positive integer n by the integral

(z) =



−1

(1 − t

)

(z − t)

n+1

dt, z /∈[−1, 1].

Use Rodriguez’ formula to show that for x ∈[−1, 1] we have

(x + i) − Q

(x − i) =−iπ P

(x),

680 18 Applications of complex variables

where P

(x) is the Legendre polynomial. Show further that Q

(z) satisfies the conditions

for the validity of an unsubtracted dispersion relation, and hence deduce Neumann’s

formula:

(z) =



−1

(t)

z − t

dt, z /∈[−1, 1].

18.2.1 Kramers–Kronig relations

Causality is the usual source of analyticity in physical applications. If G(t) is a response

function

response

(t) =



∞

−∞

G(t − t



cause



) dt



(18.58)

then for no effect to anticipate its cause we must have G(t) = 0 for t < 0. The Fourier

transform

G(ω) =



∞

−∞

iωt

G(t) dt (18.59)

is then automatically analytic everywhere in the upper half-plane. Suppose, for example,

we look at a forced, damped, harmonic oscillator whose displacement x(t) obeys

¨x + 2γ ˙x + (

+ γ

)x = F(t), (18.60)

where the friction coefficient γ is positive. As we saw earlier, the solution is of the form

x(t) =



∞

−∞

G(t, t



)F(t



)dt



where the Green function G(t, t



) = 0ift < t



. In this case

G(t, t



) =

⎧

⎨

⎩



−1

−γ(t−t



)

sin (t − t



) t > t



0, t < t



(18.61)

and so

x(t) =





−∞

−γ(t−t



)

sin (t − t



) F(t



) dt



. (18.62)

Because the integral extends only from 0 to +∞, the Fourier transform of G(t,0),

G(ω) ≡





∞

iωt

−γ t

sin tdt, (18.63)

18.2 The Schwarz reflection principle 681

is nicely convergent when Im ω>0, as evidenced by

G(ω) =−

(ω + iγ)

− 

(18.64)

having no singularities in the upper half-plane.

Another example of such a causal function is provided by the complex, frequency-

dependent, refractive index of a material n(ω). This is defined so that a travelling wave

takes the form

ϕ(x, t) = e

in(ω)k·x−iωt

. (18.65)

We can decompose n into its real and imaginary parts

n(ω) = n

(ω) + in

(ω)

= n

(ω) +

2|k|

γ(ω) (18.66)

where γ is the extinction coefficient, defined so that the intensity falls off as I ∝

exp(−γ n · x), where n = k/|k| is the direction of propagation. A non-zero γ can arise

from either energy absorption or scattering out of the forward direction.

Being a causal response, the refractive index extends to a function analytic in the

upper half-plane and n(ω) for real ω is the boundary value

n(ω)

physical

= lim

→0

n(ω + i) (18.67)

of this analytic function. Because a real (E = E

∗

) incident wave must give rise to a real

wave in the material, and because the wave must decay in the direction in which it is

propagating, we have the reality conditions

γ(−ω + i) =−γ(ω+ i),

(−ω + i) =+n

(ω + i) (18.68)

with γ positive for positive frequency.

Many materials have a frequency range |ω| < |ω

min

| where γ = 0, so the material is

transparent. For any such material n(ω) obeys the Schwarz reflection principle and so

there is an analytic continuation into the lower half-plane. At frequencies ω where the

material is not perfectly transparent, the refractive index has an imaginary part even when

ω is real. By Schwarz, n must be discontinuous across the real axis at these frequencies:

If a pole in a response function manages to sneak into the upper half-plane, then the system will be unstable

to exponentially growing oscillations. This may happen, for example, when we design an electronic circuit

containing a feedback loop. Such poles, and the resultant instabilities, can be detected by applying the

principle of the argument from the last chapter. This method leads to the Nyquist stability criterion.

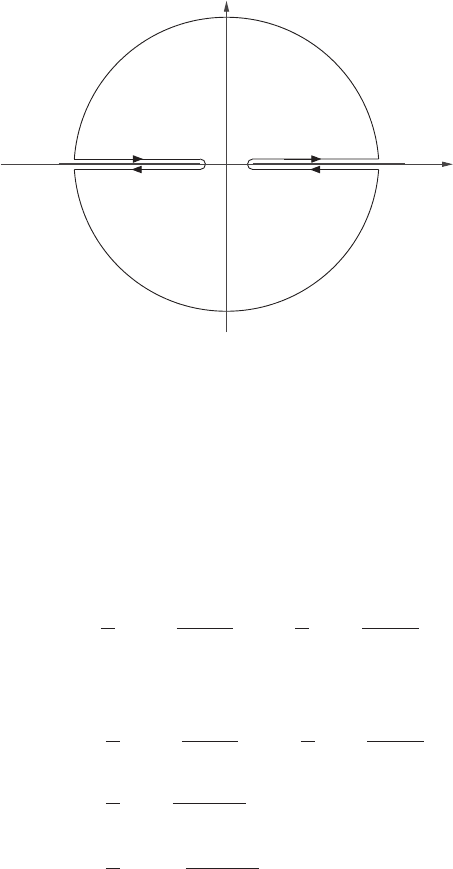
682 18 Applications of complex variables

Im 

Re 

– 

min



min

Figure 18.11 Contour for the n − 1 dispersion relation.

n(ω + i) = n

+ in

= n(ω − i) = n

− in

. These discontinuities of 2in

usually

correspond to branch cuts.

No substance is able to respond to infinitely high frequency disturbances, so n → 1

as |ω|→∞, and we can apply our dispersion relation technology to the function n −1.

We will need the contour shown in Figure 18.11, which has cuts for both positive and

negative frequencies.

By applying the dispersion-relation strategy, we find

n(ω) = 1 +



min

−∞

(ω



)



− ω

dω





∞

min

(ω



)



− ω

dω



(18.69)

for ω within the contour. Using Plemelj we can now take ω onto the real axis to get

(ω) = 1 +



min

−∞

(ω



)



− ω

dω





∞

min

(ω



)



− ω

dω



= 1 +



∞

min

(ω



)



− ω

dω

2

= 1 +



∞

min

γ(ω



)



− ω

dω



. (18.70)

In the second line we have used the anti-symmetry of n

(ω) to combine the positive and

negative frequency range integrals. In the last line we have used the relation ω/k = c to

make connection with the way this equation is written in R. G. Newton’s authoritative

Scattering Theory of Waves and Particles. This relation, between the real and absorptive

parts of the refractive index, is called a Kramers–Kronig dispersion relation, after the

original authors.

H. A. Kramers, Nature, 117 (1926) 775; R. de L. Kronig, J. Opt. Soc. Am., 12 (1926) 547.

18.2 The Schwarz reflection principle 683

If n → 1 fast enough that ω

(n − 1) → 0as|ω|→∞, we can take the f in the

dispersion relation to be ω

(n − 1) and deduce that

= 1 +



∞

min







γ(ω



)



− ω

dω



, (18.71)

another popular form of Kramers–Kronig. This second relation implies the first, but not

vice versa, because the second demands more restrictive behaviour for n(ω).

Similar equations can be derived for other causal functions. A quantity closely related

to the refractive index is the frequency-dependent dielectric “constant”

(ω) = 

+ i

. (18.72)

Again  → 1as|ω|→∞, and, proceeding as before, we deduce that



(ω) = 1 +



∞

min



(ω



)



− ω

dω

2

. (18.73)

18.2.2 Hilbert transforms

Suppose that f (x) is the boundary value on the real axis of a function everywhere analytic

in the upper half-plane, and suppose further that f (z) → 0as|z|→∞there. Then

we have

f (z ) =

2πi



∞

−∞

f (x)

x − z

dx (18.74)

for z in the upper half-plane. This is because we may close the contour with an upper

semicircle without changing the value of the integral. For the same reason the integral

must give zero when z is taken in the lower half-plane. Using the Plemelj formulæ we

deduce that on the real axis,

f (x) =

πi



∞

−∞

f (x



)



− x



. (18.75)

We can use this strategy to derive the Kramers–Kronig relations even if n

never vanishes,

and so we cannot use the Schwarz reflection principle.

The relation (18.75) suggests the definition of the Hilbert transform, Hψ, of a function

ψ(x),as

(Hψ)(x) =



∞

−∞

ψ(x



)

x − x



. (18.76)

Note the interchange of x, x



in the denominator of (18.76) when compared with (18.75).

This switch is to make the Hilbert transform into a convolution integral. Equation (18.75)

684 18 Applications of complex variables

shows that a function that is the boundary value of a function analytic and tending to zero

at infinity in the upper half-plane is automatically an eigenvector of H with eigenvalue

−i. Similarly a function that is the boundary value of a function analytic and tending

to zero at infinity in the lower half-plane will be an eigenvector with eigenvalue +i.(A

function analytic in the entire complex plane and tending to zero at infinity must vanish

identically by Liouville’s theorem.)

Returning now to our original f , which had eigenvalue −i, and decomposing it as

f (x) = f

(x) + if

(x), we find that (18.75) becomes

(x) = (Hf

)(x),

(x) =−(Hf

)(x). (18.77)

Conversely, if we are given a real function u(x) and set v (x ) = (Hu)(x ), then, under

some mild restrictions on u (that it lie in some L

(R), p > 1, for example, in which case

v(x) is also in L

(R)) the function

f (z ) =

2πi



∞

−∞

u(x ) + iv(x)

x − z

dx (18.78)

will be analytic in the upper half-plane, tend to zero at infinity there and have u(x)+iv(x)

as its boundary value as z approaches the real axis from above. The last line of (18.77)

therefore shows that we may recover u(x) from v(x) as u(x) =−(Hv)(x). The Hilbert

transform H : L

(R) → L

(R) is therefore invertible, and its inverse is given by

−1

=−H. (Note that the Hilbert transform of a constant is zero, but the L

(R)

condition excludes constants from the domain of H , and so this fact does not conflict

with invertibility.)

Hilbert transforms are useful in signal processing. Given a real signal X

(t) we can

take its Hilbert transform so as to find the corresponding imaginary part, X

(t), which

serves to make the sum

Z(t) = X

(t) + iX

(t) = A(t)e

iφ(t)

(18.79)

analytic in the upper half-plane. This complex function is the analytic signal.

The real

quantity A(t) is then known as the instantaneous amplitude,orenvelope, while φ(t) is

the instantaneous phase and

(t) =

φ(t) (18.80)

is called the instantaneous frequency (IF). These quantities are used, for example, in

narrow-band FM radio, in NMR, in geophysics and in image processing.

D. Gabor, J. Inst. Elec. Eng. (Part 3), 93 (1946) 429.