Stone M., Goldbart P. Mathematics for Physics: A Guided Tour for Graduate Students
Подождите немного. Документ загружается.


19.2 Linear differential equations 715
It is straightforward, but a trifle tedious, to show that
(z − z
1
)
r
(z − z
2
)
s
(z − z
3
)
t
P
⎧
⎨
⎩
z
1
z
2
z
3
αβγz
α
β
γ
⎫
⎬
⎭
= P
⎧
⎨
⎩
z
1
z
2
z
3
α +r β + s γ + tz
α
+ r β
+ s γ
+ t
⎫
⎬
⎭
, (19.49)
provided r + s + t = 0. Riemann’s equation retains its form under Möbius maps, only
the location of the singular points changing. We therefore deduce that
P
⎧
⎨
⎩
z
1
z
2
z
3
αβγz
α
β
γ
⎫
⎬
⎭
= P
⎧
⎨
⎩
z
1
z
2
z
3
αβγz
α
β
γ
⎫
⎬
⎭
, (19.50)
where
z
=
az + b
cz + d
, z
1
=
az
1
+ b
cz
1
+ d
, z
2
=
az
2
+ b
cz
2
+ d
, z
3
=
az
3
+ b
cz
3
+ d
. (19.51)
By using the Möbius map that takes (z
1
, z
2
, z
3
) → (0, 1, ∞), and by extracting powers
to shift the exponents, we can reduce the general eight-parameter Riemann equation to
the three-parameter hypergeometric equation.
The P symbol for the hypergeometric equation is
P
⎧
⎨
⎩
0 ∞ 1
0 a 0 z
1 − cbc− a − b
⎫
⎬
⎭
. (19.52)
By using this observation and a suitable Möbius map we see that
F(a, b; a + b − c;1− z)
and
(1 − z)
c−a−b
F(c − b, c − a; c − a − b + 1; 1 − z)
are also solutions of the hypergeometric equation, each having pure (as opposed to a
linear combination of) power-law behaviours near z = 1. (The previous solutions had
pure power-lawbehaviours near z = 0.) These new solutions must be linear combinations
of the old ones, and we may use
F(a, b; c;1) =
(c)(c − a − b)
(c − a)(c − b)
,Re(c − a − b)>0, (19.53)

716 19 Special functions and complex variables
together with the trick of substituting z = 0 and z = 1, to determine the coefficients and
show that
F(a, b; c; z)
=
(c)(c − a − b)
(c − a)(c − b)
F(a, b; a + b − c;1− z)
+
(c)(a + b − c)
(a)(b)
(1 − z)
c−a−b
F(c − b, c − a; c − a − b + 1; 1 − z).
(19.54)
This last equation holds for all values of a, b, c such that the Gamma functions make
sense.
A complete set of pure-power solutions to the hypergeometric equation can be
taken to be
φ
(0)
0
(z) = F(a, b; c; z),
φ
(1)
0
(z) = z
1−c
F(a + 1 − c, b + 1 − c;2− c; z),
φ
(0)
1
(z) = F(a, b;1− c + a + b;1− z),
φ
(1)
1
(z) = (1 − z)
c−a−b
F(c − a, c − b;1+ c − a − b;1− z),
φ
(0)
∞
(z) = z
−a
F(a, a + 1 − c;1+ a − b; z
−1
),
φ
(1)
∞
(z) = z
−b
F(a, b + 1 − c;1− a + b; z
−1
). (19.55)
Here the suffix denotes the point at which the solution has pure-power behaviour. The
connection coefficients relating the solutions to one another are then
φ
(0)
0
=
(c)(c − a − b)
(c − a)(c − b)
φ
(0)
1
+
(c)(a + b − c)
(a)(b)
φ
(1)
1
,
φ
(1)
0
=
(2 − c)(c − a − b)
(1 − a)(1 − b)
φ
(0)
1
+
(2 − c)(a + b − c)
(a + 1 − c)(b + 1 − c)
φ
(1)
1
, (19.56)
and
φ
(0)
0
= e
−iπ a
(c)(b − a)
(c − a)(b)
φ
(0)
∞
+ e
−iπ b
(2 − c)(a − b)
(a + 1 − c)(1 − b)
φ
(1)
∞
,
φ
(1)
0
= e
−iπ(a+1−c)
(2 − c)(b − a)
(b + 1 − c)(1 − a)
φ
(0)
∞
+ e
−iπ(b+1−c)
(2 − c)(a − b)
(a + 1 − c)(1 − b)
φ
(1)
∞
. (19.57)
These relations assume that Im z > 0. The signs in the exponential factors must be
reversed when Im z < 0.
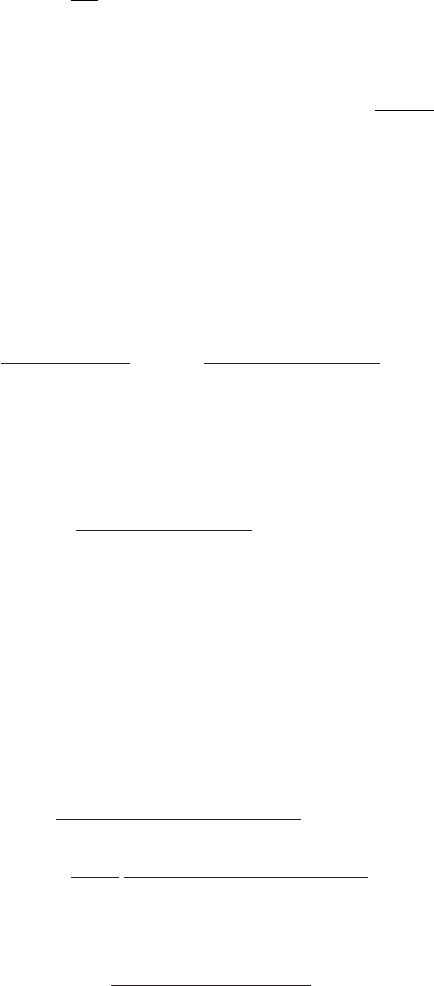
19.2 Linear differential equations 717
Example: The Pöschel–Teller problem for general positive l. A substitution z = (1 +
e
2x
)
−1
shows that the Pöschel–Teller–Schrödinger equation
−
d
2
dx
2
− l(l + 1)sech
2
x
ψ = Eψ (19.58)
has solution
ψ(x) = (1 + e
2x
)
−κ/2
(1 + e
−2x
)
−κ/2
F
κ + l +1, κ − l; κ + 1;
1
1 + e
2x
, (19.59)
where E =−κ
2
. This solution behaves near x =∞as
ψ ∼ e
−κx
F(κ + l + 1, κ − l; κ+;0) = e
−κx
. (19.60)
We use the connection formula (19.54) to see that it behaves in the vicinity of x =−∞as
ψ ∼ e
κx
F(κ + l + 1, κ − l; κ + 1; 1 − e
2x
)
→ e
κx
(κ + 1)(−κ)
(−l)(1 + l)
+ e
−κx
(κ + 1)(κ)
(κ + l + 1)(κ − l)
. (19.61)
To find the bound-state spectrum, assume that κ is positive. Then E =−κ
2
will be an
eigenvalue provided that the coefficient of e
−κx
near x =−∞vanishes. In other words,
the spectrum follows from the condition
(κ + 1)(κ)
(κ + l + 1)(κ − l)
= 0. (19.62)
This condition is satisfied for a finite set κ
n
, n = 1, ..., 0l1(where 0l1denotes the integer
part of l) at which κ is positive but κ − l is zero or a negative integer.
By setting κ =−ik, for real k we find the scattering solution
ψ(x) =
e
ikx
+ r(k)e
−ikx
, x 0
t(k)e
ikx
, x 0
(19.63)
where
r(k) =
(l +1 − ik)(−ik − l)(ik)
(−l)(1 + l)(ik)
=−
sin πl
π
(l +1 − ik)(−ik − l)(ik)
(−ik)
, (19.64)
and
t(k) =
(l +1 − ik)(−ik − l)
(1 − ik)(−ik)
. (19.65)

718 19 Special functions and complex variables
Whenever l is a (positive) integer, the divergent factor of (−l) in the denominator of
r(k) causes the reflected wave to vanish. This is something we had observed in earlier
chapters. In this reflectionless case, the transmission coefficient t(k) reduces to a phase
t(k) =
(−ik + 1)(−ik + 2) ···(−ik + l)
(−ik − 1)(−ik − 2) ···(−ik − l)
. (19.66)
19.3 Solving ODEs via contour integrals
Our task in this section is to understand the origin of contour integral solutions, such as
the expression
F(a, b; c; z) =
(c)
(b)(c − b)
1
0
(1 − tz)
−a
t
b−1
(1 − t)
c−b−1
dt, (19.67)
which we have previously seen for the hypergeometric equation.
Suppose that we are given a differential operator
L
z
= ∂
2
zz
+ p(z )∂
z
+ q(z) (19.68)
and seek a solution of L
z
u = 0 as an integral
u(z) =
F(z, t) dt (19.69)
over some contour . If we can find a kernel F such that
L
z
F =
∂Q
∂t
, (19.70)
for some function Q(z, t), then
L
z
u =
L
z
F(z, t) dt =
∂Q
∂t
dt =
[
Q
]
. (19.71)
Thus, if Q vanishes at both ends of the contour, if it takes the same value at the two ends,
or if the contour is closed and thus has no ends, then we have succeeded in our quest.
Example: Consider Legendre’s equation,
L
z
u ≡ (1 − z
2
)
d
2
u
dz
2
− 2z
du
dz
+ ν(ν + 1)u = 0. (19.72)
The identity
L
z
(t
2
− 1)
ν
(t − z)
ν+1
= (ν + 1)
d
dt
(t
2
− 1)
ν+1
(t − z)
ν+2
(19.73)

19.3 Solving ODEs via contour integrals 719
shows that
P
ν
(z) =
1
2πi
(t
2
− 1)
ν
2
ν
(t − z)
ν+1
dt (19.74)
will be a solution of Legendre’s equation, provided that
[Q]
≡
(t
2
− 1)
ν+1
(t − z)
ν+2
= 0. (19.75)
We could, for example, take a contour that encircles the points t = z and t = 1, but
excludes the point t =−1. On going round this contour, the numerator acquires a phase
of e
2πi(ν+1)
, while the denominator of [Q]
acquires a phase of e
2πi(ν+2)
. The net phase
change is therefore e
−2πi
= 1. The function in the integrated-out part is therefore single-
valued, and so the integrated-out part vanishes. When ν is an integer, Cauchy’s formula
shows that (19.74) reduces to
P
n
(z) =
1
2
n
n!
d
n
dz
n
(z
2
− 1)
n
, (19.76)
which is Rodriguez’ formula for the Legendre polynomials.
The figure-of-eight contour shown in Figure 19.2 gives us a second solution
Q
ν
(z) =
1
4i sin πν
(t
2
− 1)
ν
2
ν
(z − t)
ν+1
dt, ν/∈ Z. (19.77)
Here we define arg(t −1) and arg(t +1) to be zero for t > 1 and t > −1 respectively. The
integrated-out part vanishes because the phase gained by the (t
2
−1)
ν+1
in the numerator
of [Q]
during the clockwise winding about t = 1 is undone during the anticlockwise
winding about t =−1, and, provided that z lies outside the contour, there is no phase
change in the (z −t)
(ν+2)
in the denominator.
When ν is real and positive the contributions from the circular arcs surrounding t =±1
become negligeable as we shrink this new contour down onto the real axis. We observe
that, with the arguments of (t ± 1) as specified above,
(t
2
− 1)
ν
→ (1 − t
2
)
ν
e
−iπν
1
–1
z
Im (t)
Re (t
)
Figure 19.2 Figure-of-eight contour for Q
ν
(z).

720 19 Special functions and complex variables
for the left-going part of the contour on the real axis between t =+1 and t =−1, and
(t
2
− 1)
ν
→ (1 − t
2
)
ν
e
−iπν
e
2πiν
= (1 − t
2
)e
+iπν
after we have rounded the branch point at t =−1 and are returning along the real axis
to t =+1. Thus, after the shrinking manœuvre, the integral (19.77) becomes
Q
ν
(z) =
1
2
1
−1
(1 − t
2
)
ν
2
ν
(z − t)
ν+1
dt, ν>0. (19.78)
In contrast to (19.77), this last formula continues to make sense when ν is a positive
integer. It then provides a convenient definition of Q
n
(z), the Legendre function of the
second kind (see Exercise 18.3).
It is usually hard to find a suitable F(z, t) in one fell swoop. (The identity (19.73)
exploited in the example is not exactly obvious!) An easier strategy is to seek a solution
in the form of an integral operator with kernel K acting on the function v(t). Thus we try
u(z) =
K(z, t)v (t) dt. (19.79)
Suppose that L
z
K(z, t) = M
t
K(z, t), where M
t
is a differential operator in t that does
not involve z. The operator M
t
will have a formal adjoint M
†
t
such that
v(M
t
K) dt −
K(M
†
t
v) dt =
[
Q(K , v)
]
. (19.80)
(This is Lagrange’s identity.) Now
L
z
u =
L
z
K(z, t)v dt
=
(M
t
K(z, t))v dt
=
K(z, t)(M
†
t
v) dt +
[
Q(K , v)
]
.
We can therefore solve the original equation, L
z
u = 0, by finding a v such that (M
†
t
v) =
0, and a contour with endpoints such that
[
Q(K , v)
]
= 0. This may sound complicated,
but an artful choice of K can make it much simpler than solving the original problem. A
single K will often work for families of related equations.
Example: We will solve
L
z
u =
d
2
u
dz
2
− z
du
dz
+ νu = 0, (19.81)

19.3 Solving ODEs via contour integrals 721
by using the kernel K(z, t) = e
−zt
. It is easy to check that L
z
K(z, t) = M
t
K(z, t) where
M
t
= t
2
− t
∂
∂t
+ ν, (19.82)
and so
M
†
t
= t
2
+
∂
∂t
t + ν = t
2
+ (ν + 1) + t
∂
∂t
. (19.83)
The equation M
†
t
v = 0 has a solution
v(t) = t
−(ν+1)
e
−
1
2
t
2
, (19.84)
and so
u =
t
−(1+ν)
e
−(zt+
1
2
t
2
)
dt, (19.85)
for some suitable .
19.3.1 Bessel functions
As an illustration of the general method we will explore the theory of Bessel functions.
Bessel functions are members of the family of confluent hypergeometric functions,
obtained by letting the two regular singular points z
2
, z
3
of the Riemann–Papperitz
equation coalesce at infinity. The resulting singular point is no longer regular, and con-
fluent hypergeometric functions have an essential singularity at infinity. The confluent
hypergeometric equation is
zy
+ (c − z)y
− ay = 0, (19.86)
with solution
(a, c; z) =
(c)
(a)
∞
n=0
(a + n)
(c + n)(n + 1)
z
n
. (19.87)
Observe that
(a, c; z) = lim
b→∞
F(a, b; c; z/b). (19.88)
The second solution, provided that c is not an integer, is
z
1−c
(a − c + 1, 2 − c; z). (19.89)

722 19 Special functions and complex variables
Other functions of this family are the parabolic cylinder functions, which in special
cases reduce to e
−z
2
/4
times the Hermite polynomials, the error function,
erf (z) =
z
0
e
−t
2
dt = z
1
2
,
3
2
; −z
2
(19.90)
and the Laguerre polynomials,
L
m
n
=
(n + m + 1)
(n + 1)(m + 1)
(−n, m + 1; z). (19.91)
Bessel’s equation involves the operator
L
z
= ∂
2
zz
+
1
z
∂
z
+
1 −
ν
2
z
2
. (19.92)
Experience shows that for Bessel functions a useful kernel is
K(z, t) =
z
2
ν
exp
t −
z
2
4t
. (19.93)
Then
L
z
K(z, t) =
∂
t
−
ν + 1
t
K(z, t) (19.94)
so, again, M is a first-order operator, which is simpler to deal with than the original
second-order L
z
. In this case the adjoint is
M
†
=
−∂
t
−
ν + 1
t
(19.95)
and we need a v such that
M
†
v =−
∂
t
+
ν + 1
t
v = 0. (19.96)
Clearly, v = t
−ν−1
will work. The integrated-out part is
[Q(K , v)]
b
a
=
t
−ν−1
exp
t −
z
2
4t
b
a
, (19.97)
and we see that
J
ν
(z) =
1
2πi
z
2
ν
t
−ν−1
e
t−
z
2
4t
dt (19.98)
solves Bessel’s equation provided we use a suitable contour.
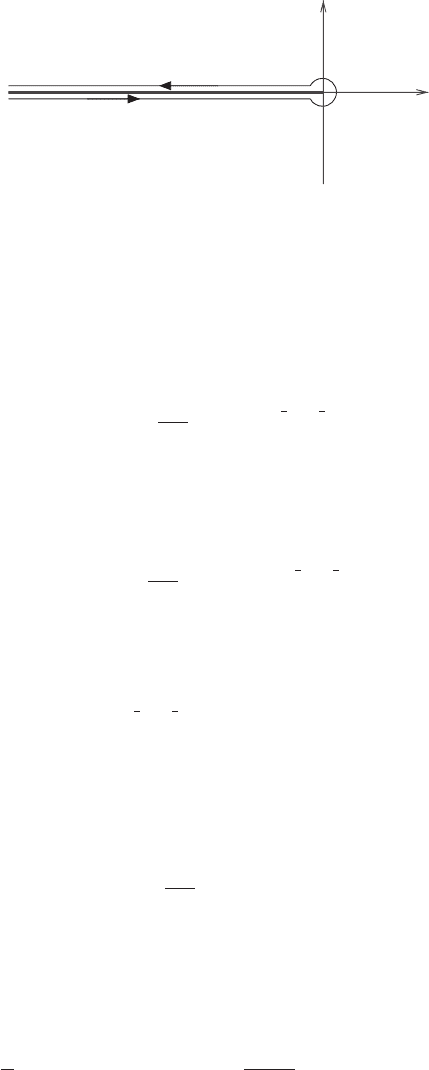
19.3 Solving ODEs via contour integrals 723
C
Im(t)
Re(t
)
Figure 19.3 Contour for solving the Bessel equation.
We can take for a curve C starting at −∞ − i and ending at −∞ + i, and
surrounding the branch cut of t
−ν−1
, which we take as the negative t axis (Figure 19.3).
This contour works because Q is zero at both ends of the contour.
A cosmetic rewrite t = uz/2 gives
J
ν
(z) =
1
2πi
C
u
−ν−1
e
z
2
u−
1
u
du. (19.99)
For ν an integer, there is no discontinuity across the cut, so we can ignore it and take C
to be the unit circle. Then, recognizing the resulting
J
n
(z) =
1
2πi
|z|=1
u
−n−1
e
z
2
u−
1
u
du (19.100)
to be a Laurent coefficient, we obtain the familiar Bessel-function generating function
e
z
2
u−
1
u
=
∞
n=−∞
J
n
(z)u
n
. (19.101)
When ν is not an integer, we see why we need a branch cut integral.
If we set u = e
w
we get
J
ν
(z) =
1
2πi
C
dw e
z sinh
w−νw
, (19.102)
where C
goes from (∞−iπ) to −iπ to +iπ to (∞+iπ); see Figure 19.4.
If we set w = t ±iπ on the horizontals and w = iθ on the vertical part, we can rewrite
this as
J
ν
(z) =
1
π
π
0
cos(νθ − z sin θ)dθ −
sin νπ
π
∞
0
e
−νt−z sinh t
dt. (19.103)
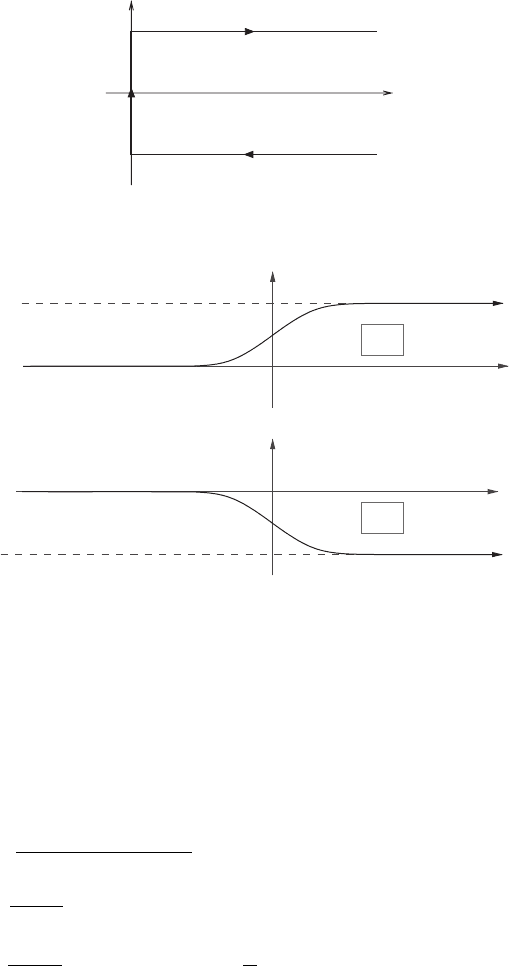
724 19 Special functions and complex variables
+ i
–
Re(w)
Im(w)
Figure 19.4 Bessel contour after the changes of variables.
+i
–i
H
(1)
H
(2)
Figure 19.5 Contours defining H
(1)
ν
(z) and H
(2)
ν
(z).
All these are standard formulæ for the Bessel function but their origins would be hard to
understand without the contour solutions trick.
When ν becomes an integer, the functions J
ν
(z) and J
−ν
(z) are no longer independent.
In order to have a Bessel-equation solution that retains its independence from J
ν
(z), even
as ν becomes a whole number, we define the Neumann function by
N
ν
(z)
def
=
J
ν
(z) cos νπ − J
−ν
(z)
sin νπ
=
cot νπ
π
π
0
cos(νθ − z sin θ)dθ − cosec νππ
π
0
cos(νθ + z sin θ)dθ
−
cos νπ
π
∞
0
e
−νt−z sinh t
dt −
1
π
∞
0
e
νt−z sinh t
dt. (19.104)
Both the Bessel and Neumann functions are real for positive real x.Asx becomes
large they oscillate as slowly decaying sines and cosines. It is sometimes convenient to
decompose these real functions into solutions that oscillate as e
±ix
. We therefore define
