Stone M., Goldbart P. Mathematics for Physics: A Guided Tour for Graduate Students

Подождите немного. Документ загружается.

19.5 Elliptic functions 735

19.5 Elliptic functions

The subject of elliptic functions goes back to the remarkable identities of Guilio Fagnano

(1750) and Leonhard Euler (1761). Euler’s formula is



√

1 − x





1 − y



√

1 − z

, (19.143)

where 0 ≤ u, v ≤ 1, and

r =

√

1 − v

+ v

√

1 − u

1 + u

. (19.144)

This looks mysterious, but perhaps so does



√

1 − x





1 − y



√

1 − z

, (19.145)

where

r = u



1 − v

+ v



1 − u

, (19.146)

until you realize that the latter formula (19.146) is merely

sin(a + b) = sin a cos b + cos a sin b (19.147)

in disguise. To see this set

u = sin a, v = sin b (19.148)

and remember the integral formula for the inverse trigonometric sine function

a = sin

−1

u =



√

1 − x

. (19.149)

The Fagnano–Euler formula is a similarly disguised addition formula for an elliptic

function. Just as we use the substitution x = sin y in the 1/

√

1 − x

integral, we can use

an elliptic-function substitution to evaluate elliptic integrals which involve square-roots

of quartic or cubic polynomials. Examples are



√

(t − a

)(t − a

)

, (19.150)



√

(t − a

)(t − a

)

. (19.151)

736 19 Special functions and complex variables

Note that I

can be reduced to an integral of the form I

by using a Möbius-map

substitution

t =



+ b



+ d

, dt = (ad − bc)



(ct



+ d)

(19.152)

to send a

to infinity. Indeed, we can use a suitable Möbius map to send any three of the

four points a

to 0, 1, ∞.

The idea of elliptic functions (as opposed to elliptic integrals , which are their func-

tional inverses) was known to Gauss, butAbel and Jacobi were the first to publish (1827).

For developing the general theory, the simplest elliptic function is the Weierstrass ℘.

This is really a family of functions that is parametrized by a pair of linearly independent

complex numbers or periods ω

, ω

. For a given pair of periods, the ℘ function is defined

by the double sum

℘(z) =



(m,n)=(0,0)



(z − mω

− nω

)

−

(mω

+ nω

)



. (19.153)

Helped by the counter-term, the sum is absolutely convergent, so we can rearrange the

terms to prove double periodicity

℘(z +mω

+ nω

) = ℘(z), m, n ∈ Z. (19.154)

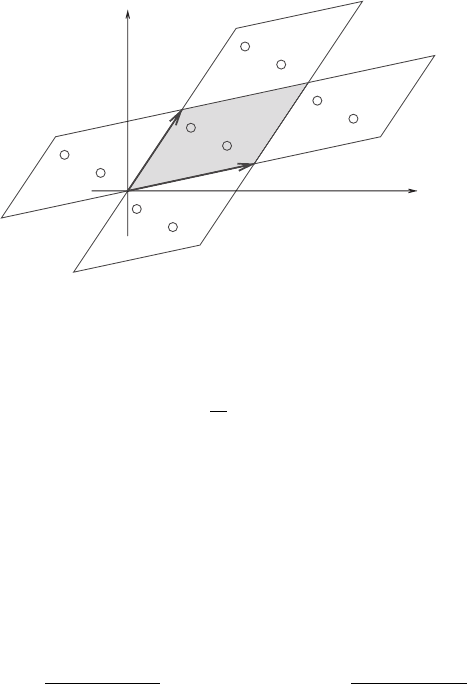
The function is thus determined everywhere by its values in the period parallelogram

P ={λω

+ µω

:0≤ λ, µ<1}. Double periodicity is the defining characteristic of

elliptic functions (Figure 19.10).

Any non-constant meromorphic function f (z) that is doubly periodic has four basic

properties:

(a) The function must have at least one pole in its unit cell, otherwise it would be

holomorphic and bounded, and therefore a constant by Liouville.

(b) The sum of the residues at the poles must add to zero. This follows from integrat-

ing f (z) around the boundary of the period parallelogram and observing that the

contributions from opposite edges cancel.

from integrating f



/f around the boundary of the period parallelogram.

(d) If f has zeros at the N points z

and poles at the N points p

then



i=1

−



i=1

= nω

+ mω

where m, n are integers. This follows from integrating zf



/f around the boundary of

the period parallelogram.

19.5 Elliptic functions 737



Figure 19.10 Unit cell and double periodicity.

The Weierstrass ℘ has a second-order pole at the origin. It also obeys

lim

|z|→0



℘(z) −



= 0,

℘(z) = ℘(−z),

℘



(z) =−℘



(−z). (19.155)

The property that makes ℘(z) useful for evaluating integrals is



℘



(z)



= 4℘

(z) − g

℘(z) − g

, (19.156)

where

= 60



(m,n)=(0,0)

(mω

+ nω

)

, g

= 140



(m,n)=(0,0)

(mω

+ nω

)

. (19.157)

Equation (19.156) is proved by examining the first few terms in the Laurent expansion

in z of the difference of the left-hand and right-hand sides. All negative powers cancel, as

does the constant term. The difference is zero at z = 0, has no poles or other singularities,

and, being continuous and periodic, is automatically bounded. It is therefore identically

zero by Liouville’s theorem.

From the symmetry and periodicity of ℘ we see that ℘



(z) = 0atω

/2, ω

/2 and

(ω

+ ω

)/2 where ℘(z) takes the values e

= ℘(ω

/2), e

= ℘(ω

/2) and e

℘ ((ω

+ω

)/2). Now ℘



must have exactly three zeros since it has a pole of order three

at the origin and, by property (c), the number of zeros in the unit cell is equal to the

number of poles. We therefore know the location of all three zeros, and can factorize:

4℘

(z) − g

℘(z) − g

= 4(℘ − e

)(℘ − e

). (19.158)

We note that the coefficient of ℘

in the polynomial on the left side is zero, implying

that e

+ e

= 0.

738 19 Special functions and complex variables

The roots e

can never coincide. For example, (℘ (z) −e

) has a double zero at ω

/2,

but two zeros is all it is allowed because the number of poles per unit cell equals the

number of zeros, and (℘ (z) − e

) has a double pole at 0 as its only singularity. Thus,

(℘ − e

) cannot be zero at another point, but it would be if e

coincided with e

or e

As a consequence, the discriminant



def

= 16(e

− e

)

− e

)

− e

)

= g

− 27g

(19.159)

is never zero.

We use ℘ and (19.156) to write

z = ℘

−1

(u) =



∞

√

(t − e

)(t − e

)



∞



− g

t − g

. (19.160)

This maps the u plane, with cuts that we can take from e

to e

and e

to ∞, one-to-one

onto the 2-torus, regarded as the unit cell of the ω

n,m

= nω

+ mω

lattice.

As z sweeps over the torus, the points x = ℘(z), y = ℘



(z) move on the elliptic curve

= 4x

− g

x − g

(19.161)

which should be thought of as a set in CP

. These curves, and the finite fields of rational

points that lie on them, are exploited in modern cryptography.

The magic that leads to addition formulæ, such as the Euler–Fagnano relation (19.144)

with which we began this section, lies in the (not immediately obvious) fact that any

elliptic function having the same periods as ℘(z) can be expressed as a rational function

of ℘(z) and ℘



(z). From this it follows (after some thought) that any two such elliptic

functions, f

(z) and f

(z), obey a relation F(f

, f

) = 0, where

F(x, y) =



m,n

n,m

(19.162)

is a polynomial in x and y. We can eliminate ℘



(z) in these relations by writing ℘



(z) =



4℘

(z) − g

℘(z) − g

Modular invariance

If ω

and ω

are periods and define a unit cell, so are



= aω

+ bω



= cω

+ dω

where a, b, c, d are integers with ad−bc =±1. This condition on the determinant ensures

that the matrix inverse also has integer entries, and so the ω

can be expressed in terms

of the ω



with integer coefficients. Consequently the set of integer linear combinations

19.5 Elliptic functions 739

of the ω



generate the same lattice as the integer linear combinations of the original ω

This notion of redefining the unit cell should be familiar to you from solid state physics.

If we wish to preserve the orientation of the basis vectors, we must restrict ourselves

to maps whose determinant ad − bc is unity. The set of such transforms constitutes the

modular group SL(2, Z). Clearly ℘ is invariant under this group, as are g

and g

and

. Now define ω

/ω

= τ , and write

(ω

, ω

) =

˜g

(τ ), g

(ω

, ω

) =

˜g

(τ ). (ω

, ω

) =

(τ ),

(19.163)

and also

J (τ ) =

˜g

− 27˜g

˜g



. (19.164)

Because the denominator is never zero when Im τ>0, the function J (τ ) is holomorphic

in the upper half-plane – but not on the real axis. The function J (τ ) is called the elliptic

modular function.

Except for the prefactors ω

, the functions ˜g

(τ ),

(τ ) and J (τ ) are invariant under

the Möbius transformation

τ →

aτ + b

cτ +d

, (19.165)

with





∈ SL(2, Z). (19.166)

This Möbius transformation does not change if the entries in the matrix are multiplied

by a common factor of ±1, and so the transformation is an element of the modular group

PSL(2, Z) ≡ SL(2, Z)/{I, −I }.

Taking into account the change in the ω

prefactors we have

˜g



aτ + b

cτ +d



= (cτ +d)

˜g

(τ ),

˜g



aτ + b

cτ +d



= (cτ +d)

˜g

(τ ),





aτ + b

cτ +d



= (cτ +d)

(τ ). (19.167)

Because c = 0 and d = 1 for the special case τ → τ + 1, these three functions obey

f (τ +1) = f (τ ) and so depend on τ only via the combination q

= e

2πiτ

. For example,

740 19 Special functions and complex variables

it is not hard to prove that

(τ ) = (2π)

∞

n=1



1 − q

. (19.168)

We can also expand these functions as power series in q

– and here things get interesting

because the coefficients have number-theoretic properties. For example

˜g

(τ ) = (2π)

+ 20

∞



n=1

(n)q

˜g

(τ ) = (2π)

216

−

∞



n=1

(n)q

. (19.169)

The symbol σ

(n) is defined by σ

(n) =

, where d runs over all positive divisors

of the number n.

In the case of the function J (τ ), the prefactors cancel and



aτ + b

cτ +d



= J (τ ), (19.170)

so J (τ ) is a modular invariant. One can show that if J (τ

) = J (τ

), then

aτ

+ b

cτ

+ d

(19.171)

for some modular transformation with integer a, b, c, d, where ad −bc = 1, and, further,

that any modular-invariant function is a rational function of J (τ ). It seems clear that

J (τ ) is rather a special object.

This J (τ ) is the function referred to on page 500 in connection with the Monster

group. As with the ˜g

, J (τ ) depends on τ only through q

. The first few terms in the

power series expansion of J(τ ) in terms of q

turn out to be

1728J (τ ) = q

−2

+ 744 + 196884q

+ 21493760q

+ 864299970q

+··· (19.172)

Since AJ (τ ) + B has all the same modular invariance properties as J (τ ), the numbers

1728 (= 12

) and 744 are just conventional normalizations. Once we set the coefficient

of q

−2

to unity, however, the remaining integer coefficients are completely determined by

the modular properties. A number-theory interpretation of these integers seemed lacking

until John McKay and others observed that

1 = 1

196884 = 1 + 196883

21493760 = 1 + 196883 + 21296786

864299970 = 2×1 + 2×196883 + 21296786 + 842609326, (19.173)

19.6 Further exercises and problems 741

where “1” and the large integers on the right-hand side are the dimensions of the smallest

irreducible representations of the Monster. This “Monstrous Moonshine” was originally

mysterious and almost unbelievable (“moonshine” = “fantastic nonsense”) but it was

explained by Richard Borcherds by the use of techniques borrowed from string theory.

Borcherds received the 1998 Fields Medal for this work.

19.6 Further exercises and problems

Exercise 19.3: Show that the binomial series expansion of (1 + x)

−ν

can be written as

(1 + x)

−ν

∞



m=0

(−x)

(m + ν)

(ν) m!

, |x| < 1.

Exercise 19.4: A Mellin transform and its inverse. Combine the Beta-function identity

(19.15) with a suitable change of variables to evaluate the Mellin transform



∞

s−1

(1 + x)

−ν

dx, ν>0,

of (1 + x)

−ν

as a product of Gamma functions. Now consider the Bromwich contour

integral

2πi (ν)



c+i∞

c−i∞

−s

(ν − s)(s) ds.

Here Re c ∈ (0, ν). The Bromwich contour therefore runs parallel to the imaginary axis

with the poles of (s) to its left and the poles of (ν − s) to its right. Use the identity

(s)(1 − s) = π cosec πs

to show that when |x| < 1 the contour can be closed by a large semicircle lying to the

left of the imaginary axis. By using the preceding exercise to sum the contributions from

the enclosed poles at s =−n, evaluate the integral.

Exercise 19.5: Mellin–Barnes integral. Use the technique developed in the preceding

exercise to show that

F(a, b, c; −x) =

(c)

2πi (a)(b)



c+i∞

c−i∞

−s

(a − s)(b − s)(s)

(c − s)

ds,

“I was in Kashmir. I had been traveling around northern India, and there was one really long tiresome bus

journey, which lasted about 24 hours. Then the bus had to stop because there was a landslide and we couldn’t

go any further. It was all pretty darn unpleasant. Anyway, I was just toying with some calculations on this

bus journey and finally I found an idea which made everything work” – Richard Borcherds (Interview in

The Guardian, August 1998).

742 19 Special functions and complex variables

for a suitable range of x. This integral representation of the hypergeometric function is

due to the English mathematician Ernest Barnes (1908), later a controversial Bishop of

Birmingham.

Exercise 19.6: Let

Y =





Show that the matrix differential equation

Y =

Y +

1 − z

Y ,

where

A =



0 a

01− c



, B =



ba+ b −c + 1



has a solution

Y (z) = F(a, b; c; z)







(a, b; c ; z)





Exercise 19.7: Kniznik–Zamolodchikov equation. The monodromy properties of solu-

tions of differential equations play an important role in conformal field theory. The

Fuchsian equations studied in this exercise are obeyed by the correlation functions in

the level-k Wess–Zumino–Witten model.

Let V

(a)

, a = 1, ...n, be spin-j

representation spaces for the group SU(2). Let

W (z

, ..., z

) be a function taking values in V

(1)

⊗ V

(2)

⊗···⊗V

(n)

. (In other words

W is a function W

,...,i

, ..., z

) where the index i

labels states in the spin-j

factor.)

Suppose that W obeys the Kniznik–Zamolodchikov (K–Z) equations

(k + 2)

∂

∂z

W =



b,b=a

(a)

· J

(b)

− z

W , a = 1, ..., n,

where

(a)

· J

(b)

≡ J

(a)

(b)

+ J

(a)

(b)

+ J

(a)

(b)

and J

(a)

indicates the su(2) generator J

acting on the V

(a)

factor in the tensor product.

If we set z

= z, for example, and fix the position of z

, ...z

, then the differential

equation in z has regular singular points at the n − 1 remaining z

(a) By diagonalizing the operator J

(a)

· J

(b)

show that there are solutions W (z) that

behave for z

close to z

W (z) ∼ (z

− z

)



−

19.6 Further exercises and problems 743

where



j(j + 1)

k + 2

, 

+ 1)

k + 2

and j is one of the spins |j

− j

|≤j ≤ j

+ j

occuring in the decomposition

of j

⊗ j

(b) Define covariant derivatives

∇

∂

∂z

−



b,b=a

(a)

· J

(b)

− z

and show that [∇

, ∇

]=0. Conclude that the effect of parallel transport of the

solutions of the K–Z equations provides a representation of the braid group of the

world-lines of the z

Appendix A

Linear algebra review

In physics we often have to work with infinite-dimensional vector spaces. Navigating

these vasty deeps is much easier if you have a sound grasp of the theory of finite-

dimensional spaces. Most physics students have studied this as undergraduates, but not

always in a systematic way. In this appendix we gather together and review those parts

of linear algebra that we will find useful in the main text.

A.1 Vector space

A.1.1 Axioms

A vector space V over a field F is a set equipped with two operations: a binary operation

called vector addition which assigns to each pair of elements x, y ∈ V a third element

denoted by x + y, and scalar multiplication which assigns to an element x ∈ V and

λ ∈ F a new element λx ∈ V . There is also a distinguished element 0 ∈ V such that the

following axioms are obeyed:

(1) Vector addition is commutative: x +y = y + x.

(2) Vector addition is associative: (x +y) + z = x + (y + z).

(3) Additive identity: 0 + x = x.

(4) Existence of an additive inverse: for any x ∈ V , there is an element (−x) ∈ V , such

that x + (−x ) = 0.

(5) Scalar distributive law (i) λ(x + y) = λx + λy.

(6) Scalar distributive law (ii) (λ + µ)x = λx + µx.

(7) Scalar multiplication is associative: (λµ)x = λ(µx).

(8) Multiplicative identity: 1x = x.

The elements of V are called vectors. We will only consider vector spaces over the field

of the real numbers, F = R,

or the complex numbers, F = C.

You have no doubt been working with vectors for years, and are saying to yourself

“I know this stuff”. Perhaps so, but to see if you really understand these axioms try the

following exercise. Its value lies not so much in the solution of its parts, which are easy,

as in appreciating that these commonly used properties both can and need to be proved

from the axioms. (Hint: work the problems in the order given; the later parts depend on

the earlier.)

In this list 1, λ, µ, ∈ F and x, y, 0 ∈ V .

744