Stone M., Goldbart P. Mathematics for Physics: A Guided Tour for Graduate Students

Подождите немного. Документ загружается.

12.5 Further exercises and problems 445

(d) Solve the partial differential equation in part (c), and hence show that the minimal-

energy solutions with winding number N > 0 are given by

ξ + iη = λ

(z − a

)...(z − a

)

(z − b

)...(z − b

)

where z = x

+ix

, and λ, a

, ..., a

and b

, ..., b

are arbitrary complex numbers

– except that no a may coincide with any b. This is the solution that we displayed at

the end of Section 12.4.2.

(e) Repeat the analysis for N < 0. Show that the solutions are given in terms of rational

functions of ¯z = x

− ix

The idea of combining the energy functional and the topological charge into a single,

manifestly positive, functional is due to Evgueny Bogomol’nyi. The resulting first-order

linear equation is therefore called a Bogomolnyi equation. If we had tried to find a solution

directly in terms of n, we would have ended up with a horribly nonlinear second-order

partial differential equation.

Exercise 12.13: Lobachevski space. The hyperbolic plane of Lobachevski geometry can

be realized by embedding the Z ≥ R branch of the two-sheeted hyperboloid Z

−X

−

= R

into a Minkowski space with metric ds

=−dZ

+ dX

+ dY

We can parametrize the embedded surface by making an “imaginary radius” version

of the stereographic map, in which the point P on the hyperboloid is labelled by the

coordinates of the point Q on the XY -plane (see Figure 12.15).

–R

Figure 12.15 A slice through the embedding of two-dimensional Lobachevski space into three-

dimensional Minkowski space, showing the stereographic parametrization of the embedded space

by the Poincaré disc X

+ Y

< R

446 12 Integration on manifolds

(i) Show that this embedding induces the metric

g( , ) =

− X

− Y

)

(dX ⊗ dX + dY ⊗ dY ), X

+ Y

< R

of the Poincaré disc model (see Problem 1.7) on the hyperboloid.

(ii) Use the induced metric to show that the area of a disc of hyperbolic radius ρ is

given by

Area = 4πR

sinh



= 2πR

(cosh(ρ/R) − 1),

and so is only given by πρ

when ρ is small compared to the scale R of the hyperbolic

space. It suffices to consider circles with their centres at the origin. You will first

need to show that the hyperbolic distance ρ from the centre of the disc to a point at

Euclidean distance r is

ρ = R ln



R + r

R − r



Exercise 12.14: Faraday’s “flux rule” for computing the electromotive force E in a circuit

containing a thin moving wire is usually derived by the following manipulations:

E ≡

∂

(E + v ×B) · dr





curl E · dS −

∂

B · (v ×dr)

=−





∂B

∂t

· dS −

∂

B · (v ×dr)

=−





B · dS.

(a) Show that if we parametrize the surface  as x

(u, v, τ), with u, v labelling points

on , and τ parametrizing the evolution of , then the corresponding manipulations

in the covariant differential-form version of Maxwell’s equations lead to

dτ





F =





F =



∂

F =−



∂

f ,

where V

= ∂x

/∂τ and f =−i

(b) Show that if we take τ to be the proper time along the world-line of each element

of , then V is the 4-velocity

√

1 − v

(1, v),

and f =−i

F becomes the 1-form corresponding to the Lorentz-force 4-vector.

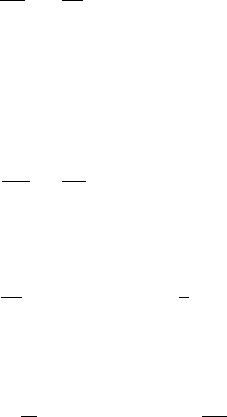
12.5 Further exercises and problems 447

It is not clear that the terms in this covariant form of Faraday’s law can be given any

physical interpretation outside the low-velocity limit. When parts of ∂ have different

velocities, the relation of the integrals to measurements made at fixed coordinate time

requires thought.

The next pair of exercises explores some physics appearances of the continuum Hopf

linking number (12.65).

Exercise 12.15: The equations governing the motion of an incompressible inviscid fluid

are ∇·v = 0 and Euler’s equation

def

∂v

∂t

+ (v ·∇)v =−∇P.

Recall that the operator ∂/∂t + v ·∇, here written as D/Dt, is called the convective

derivative.

(a) Take the curl of Euler’s equation to show that if ω =∇×v is the vorticity then

Dω

≡

∂ω

∂t

+ (v ·∇)ω = (ω ·∇)v.

(b) Combine Euler’s equation with part (a) to show that

(v · ω) =∇·





− P







f (r, t) dV =





dV .

(d) Conclude that when ω is zero at infinity the helicity

I =



v · (∇×v) dV =



v · ω dV

is a constant of the motion.

The helicity measures the Hopf linking number of the vortex lines. The discovery

its conservation launched the field of topological fluid dynamics.

Exercise 12.16: Let B =∇×A and E =−∂A/∂t −∇φ be the electric and magnetic

fields in an incompressible and perfectly conducting fluid. In such a fluid, the co-moving

electromotive force E + v × B must vanish everywhere.

See E. Marx, J. Franklin Inst., 300 (1975) 353.

H. K. Moffatt, J. Fluid Mech., 35 (1969) 117.

448 12 Integration on manifolds

(a) Use Maxwell’s equations to show that

∂A

∂t

= v × (∇×A) −∇φ,

∂B

∂t

=∇×(v × B).

(b) From part (a) show that the convective derivative of A · B is given by

(

A · B

)

=∇·

{

(

A · v − φ

)

}

at infinity, conclude that Woltjer’s invariant,



(A · B) dV =





ijk

∂

x =



AF,

is a constant of the motion.

This result shows that the Hopf linking number of the magnetic field lines is independent

of time. It is an essential ingredient in the geodynamo theory of the Earth’s magnetic

field.

An introduction to differential topology

Topology is the study of the consequences of continuity. We all know that a continuous

real function defined on a connected interval and positive at one point and negative

at another must take the value zero at some point between. This fact seems obvious

– although a course of real analysis will convince you of the need for a proof. A less

obvious fact, but one that follows from the previous one, is that a continuous function

defined on the unit circle must posses two diametrically opposite points at which it

takes the same value. To see that this is so, consider f (θ + π) − f (θ ). This difference

(if not initially zero, in which case there is nothing further to prove) changes sign as

θ is advanced through π , because the two terms exchange roles. It was therefore zero

somewhere. This observation has practical application in daily life: our local coffee shop

contains four-legged tables that wobble because the floor is not level. They are round

tables, however, and because they possess no misguided levelling screws all four legs

have the same length. We are therefore guaranteed that by rotating the table about its

centre through an angle of less than π/2 we will find a stable location. A ninety-degree

rotation interchanges the pair of legs that are both on the ground with the pair that are

rocking, and at the change-over point all four legs must be simultaneously on the ground.

Similar effects with a practical significance for physics appear when we try to extend

our vector and tensor calculus from a local region to an entire manifold. A smooth field

of vectors tangent to the sphere S

will always possess a zero – i.e. a point at which

the vector field vanishes. On the torus T

, however, we can construct a nowhere-zero

vector field. This shows that the global topology of the manifold influences the way in

which the tangent spaces are glued together to form the tangent bundle. To study this

influence in a systematic manner we need first to understand how to characterize the

global structure of a manifold, and then to see how this structure affects the mathematical

and physical objects that live on it.

13.1 Homeomorphism and diffeomorphism

In the previous chapter we met with a number of topological invariants associated with

mappings. These homotopy invariants were unaffected by continuous deformations of

a map, and served to distinguish between topologically distinct mappings. Similarly,

homology invariants help classify topologically distinct manifolds. The analogue of the

winding number is the set of Betti numbers of a manifold. If two manifolds have different

Betti numbers they are certainly distinct. Unfortunately, if two manifolds have the same

449

450 13 An introduction to differential topology

Betti numbers, we cannot be sure that they are topologically identical. It is a Holy Grail

of topology to find a complete set of invariants such that having them all coincide would

be enough to say that two manifolds were topologically the same.

In the previous paragraph we were deliberately vague in our use of the terms “distinct”

and the “same”. Two topological spaces (spaces equipped with a definition of what is

to be considered an open set) are regarded as being the “same”, or homeomorphic,

if there is a one-to-one, onto, continuous map between them whose inverse is also

continuous. Manifolds come with the additional structure of differentiability: we may

therefore talk of “smooth” maps, meaning that their expression in coordinates is infinitely

∞

) differentiable. We regard two manifolds as being the “same”, or diffeomorphic,

if there is a one-to-one onto C

∞

map between them whose inverse is also C

∞

. The

distinction between homeomorphism and diffeomorphism sounds like a mere technical

nicety, but it has consequences for physics. Edward Witten discovered

that there are

992 distinct 11-spheres. These are manifolds that are all homeomorphic to the 11-sphere,

but diffeomorphically inequivalent. This fact is crucial for the cancellation of global

gravitational anomalies in the E

× E

or SO(32) symmetric superstring theories.

Since we are interested in the consequences of topology for calculus, we shall restrict

ourselves to the interpretation “same” = diffeomorphic.

13.2 Cohomology

Betti numbers arise in answer to what seems like a simple calculus problem: when can

a vector field whose divergence vanishes be written as the curl of something? We shall

see that the answer depends on the global structure of the space the field inhabits.

13.2.1 Retractable spaces: Converse of Poincaré’s lemma

Poincaré’s lemma asserts that d

= 0. In traditional vector-calculuslanguage this reduces

to the statements curl (grad φ) = 0 and div (curl w) = 0. We often assume that the

converse is true: if curl v = 0, we expect that we can find a φ such that v = grad φ,

and if div v = 0 that we can find a w such that v = curl w. You know a formula for the

first case:

φ(x) =



v · dx, (13.1)

but you probably do not know the corresponding formula for w. Using differential forms,

and provided the space in which these forms live has suitable topological properties, it

is straightforward to find a solution for the general problem: If ω is closed, meaning that

dω = 0, find χ such that ω = dχ .

E. Witten, Comm. Math. Phys., 117 (1986) 197.

13.2 Cohomology 451

The “suitable topological properties” referred to in the previous paragraph is that the

space be retractable. Suppose that the closed form ω is defined in a domain . We say

that  is retractable to the point O if there exists a smooth map ϕ

:  →  which

depends continuously on a parameter t ∈[0, 1] and for which ϕ

(x) = x and ϕ

(x) = O.

Applying this retraction map to the form, we will then have ϕ

∗

ω = ω and ϕ

∗

ω = 0. Let

us set ϕ

) = x

(t). Define η(x, t) to be the velocity-vector field that corresponds to

the coordinate flow:

= η

(x, t). (13.2)

An easy exercise, using the interpretation of the Lie derivative in (11.41), shows that



∗



= L

(ϕ

∗

ω). (13.3)

We now use the infinitesimal homotopy relation and our assumption that dω = 0, and

hence (from Exercise 12.3) that d(ϕ

∗

ω) = 0, to write

(ϕ

∗

ω) = (i

d + di

)(ϕ

∗

ω) = d[i

(ϕ

∗

ω)]. (13.4)

Using this, we can integrate up with respect to t to find

ω = ϕ

∗

ω − ϕ

∗

ω = d





(ϕ

∗

ω)dt



. (13.5)

Thus

χ =



(ϕ

∗

ω)dt (13.6)

solves our problem.

This magic formula for χ makes use of nearly all the “calculus on manifolds” concepts

that we have introduced so far. The notation is so powerful that it has also suppressed

nearly everything that a traditionally educated physicist would find familiar. We will

therefore unpack the symbols by means of a concrete example. Let us take  to be the

whole of R

. This can be retracted to the origin via the map ϕ

) = x

(t) = tx

. The

velocity field whose flow gives

(t) = tx

(1)

is η

(x, t) = x

/t. To verify this, compute

(t)

= x

(1) =

(t),

452 13 An introduction to differential topology

so x

(t) is indeed the solution to

= η

(x(t), t).

Now let us apply this retraction to ω = Adydz +Bdzdx +Cdxdy with

dω =



∂A

∂x

∂B

∂y

∂C

∂z



dxdydz = 0. (13.7)

The pull-back ϕ

∗

gives

∗

ω = A(tx, ty, tz )d(ty)d(tz) + (two similar terms). (13.8)

The interior product with

η =



∂

∂x

+ y

∂

∂y

+ z

∂

∂z



(13.9)

then gives

∗

ω = tA(tx, ty, tz )(ydz− zdy) + (two similar terms). (13.10)

Finally we form the ordinary integral over t to get

χ =



(ϕ

∗

ω)dt





A(tx, ty, tz)tdt



(ydz − zdy)





B(tx, ty, tz)tdt



(zdx − xdz)





C(tx, ty, tz)tdt



(xdy − ydx). (13.11)

In this expression the integrals in the square brackets are just numerical coefficients, i.e.

the “dt” is not part of the 1-form. It is instructive, because not entirely trivial, to let “d”

act on χ and verify that the construction works. If we focus first on the term involving

A, we find that d[



A(tx, ty, tz)tdt](ydz − zdy) can be grouped as







2tA + t



∂A

∂x

+ y

∂A

∂y

+ z

∂A

∂z





dydz

−



∂A

∂x

dt (xdydz + ydzdx + zdxdy). (13.12)

13.2 Cohomology 453

The first of these terms is equal to







A(tx, ty, tz)





dydz = A(x, y, x) dydz, (13.13)

which is part of ω. The second term will combine with the terms involving B, C,to

become

−





∂A

∂x

∂B

∂y

∂C

∂z



dt (xdydz + ydzdx + zdxdy), (13.14)

which is zero by our hypothesis. Putting together the A, B , C terms does, therefore,

reconstitute ω.

13.2.2 Obstructions to exactness

The condition that  be retractable plays an essential role in the converse to Poincaré’s

lemma. In its absence, dω = 0 does not guarantee that there is an χ such that ω = dχ.

Consider, for example, a vector field v with curl v ≡ 0 in a two-dimensional annulus

 ={R

< |r| < R

}. In the annulus (a non-retractable space) the condition that

curl v ≡ 0 does not prohibit



v · dr being non-zero for some closed path  encircling

the central hole. When this line integral is non-zero then there can be no single-valued

χ such that v = grad χ . If there were such a χ, then



v · dr = χ(0) − χ(0) = 0. (13.15)

A non-zero value for



v · dr therefore constitutes an obstruction to the existence of a

χ such that v = grad χ .

Example: The sphere S

is not retractable: any attempt to pull its points back to the north

pole will necessarily tear a hole in the surface somewhere. Related to this fact is that

whilst the area 2-form sin θdθdφ is closed, it cannot be written as the d of something.

We can try to write

sin θdθ dφ = d[(1 − cos θ)dφ], (13.16)

but the 1-form (1 − cos θ)dφ is singular at the south pole, θ = π. We could try

sin θdθ dφ = d[(−1 − cos θ)dφ], (13.17)

454 13 An introduction to differential topology

but this is singular at the north pole, θ = 0. There is no escape. We know that



sin θdθ dφ = 4π , (13.18)

but if sin θ dθdφ = dχ then Stokes’ theorem says that



sin θdθ dφ



∂S

χ = 0 (13.19)

because ∂S

=∅. Again, a non-zero value for



ω over some boundary-less region has

provided an obstruction to finding an χ such that ω = dχ .

13.2.3 De Rham cohomology

We have seen that, sometimes, the condition dω = 0 allows us to find a χ such that

ω = dχ, and sometimes it does not. If the region in which we seek χ is retractable,

we can always construct it. If the region is not retractable there may be an obstruction

to the existence of χ . In order to describe the various possibilities we introduce the

language of cohomology, or more precisely de Rham cohomology, named for the Swiss

mathematician Georges de Rham who did the most to create it.

For simplicity, suppose that we are working in a compact manifold M without bound-

ary. Let 

(M ) =

∗

M ) be the space of all smooth p-form fields. It is a vector

space over R: we can add p-form fields and multiply them by real constants, but, as

is the vector space C

∞

(M ) of smooth functions on M , it is infinite dimensional. The

subspace Z

(M ) of closed forms – those with dω = 0 – is also an infinite-dimensional

vector space, and the same is true of the space B

(M ) of exact forms – those that can be

written as ω = dχ for some globally defined (p − 1)-form χ. Now consider the space

= Z

, which is the space of closed forms modulo exact forms. In this space we do

not distinguish between two forms, ω

and ω

when there is a χ, such that ω

= ω

+dχ .

We say that ω

and ω

are cohomologous in H

(M ), and write ω

∼ ω

. We will use

the symbol [ω] to denote the equivalence class of forms cohomologous to ω. Now a

miracle happens! For a compact manifold M , the space H

(M ) is finite dimensional! It

is called the p-th (de Rham) cohomology space of the manifold, and depends only on

the global topology of M . In particular, it does not depend on any metric we may have

chosen for M.

Sometimes we write H

(M , R) to make clear that we are dealing with de Rham

cohomology, and that we are working with vector spaces over the real numbers. This is

because there is also a valuable space H

(M , Z), where we only allow multiplication

by integers.

The cohomology space H

(M , R) codifies all potential obstructions to solving the

problem of finding a (p −1)-form χ such that dχ = ω: we can find such a χ if and only

if ω is cohomologous to zero in H

(M , R).IfH

(M , R) ={0}, which is the case if M

is retractable, then all closed p-forms are cohomologous to zero. If H

(M , R) ={0},