Stone M., Goldbart P. Mathematics for Physics: A Guided Tour for Graduate Students

Подождите немного. Документ загружается.

13.3 Homology 455

then some closed p-forms ω will not be cohomologous to zero. We can test whether

ω ∼ 0 ∈ H

(M , R) by forming suitable integrals.

13.3 Homology

To understand what the suitable integrals, of the last section are, we need to think about

the spaces that are the cohomology spaces’ vector-space duals. These homology spaces

are simple to understand pictorially.

The basic idea is that, given a region , we can find its boundary ∂. Inspection of

a few simple cases will soon lead to the conclusion that the “boundary of a boundary”

consists of nothing. In symbols, ∂

= 0. The statement “∂

= 0” is clearly analogous

to “d

= 0”, and, pursuing the analogy, we can construct a vector space of “regions”

and define two “regions” as being homologous if they differ by the boundary of another

“region”.

13.3.1 Chains, cycles and boundaries

We begin by making precise the vague notions of region and boundary.

Simplicial complexes

The set of all curves and surfaces in a manifold M is infinite dimensional, but the

homology spaces are finite dimensional. Life would be much easier if we could use

finite-dimensional spaces throughout. Mathematicians therefore do what any computa-

tionally minded physicist would do: they approximate the smooth manifold by a discrete

polygonal grid.

Were they interested in distances, they would necessarily use many

small polygons so as to obtain a good approximation to the detailed shape of the mani-

fold. The global topology, though, can often be captured by a rather coarse discretization.

The result of this process is to reduce a complicated problem in differential geometry to

one of simple algebra. The resulting theory is therefore known as algebraic topology.

It turns out to be convenient to approximate the manifold by generalized trian-

gles. We therefore dissect M into line segments (if one-dimensional), triangles (if

two-dimensional), tetrahedra (if three-dimensional) or higher-dimensional p-simplices

(singular: simplex). The rules for the dissection are (see Figure 13.1):

(a) Every point must belong to at least one simplex.

(b) A point can belong to only a finite number of simplices.

This discrete approximation leads to what is known as simplicial homology. Simplicial homology is rather

primitive and old fashioned, having been supplanted by singular homology and the theory of CW complexes.

The modern definitions are superior for proving theorems, but are less intuitive, and for smooth manifolds

lead to the same conclusions as the simpler-to-describe simplicial theory.

456 13 An introduction to differential topology

(a) (b)

Figure 13.1 Triangles, or 2-simplices, that are (a) allowed, (b) not allowed in a dissection. In (b)

the problem is that only parts of edges are in common.

ββ

(a) (b)

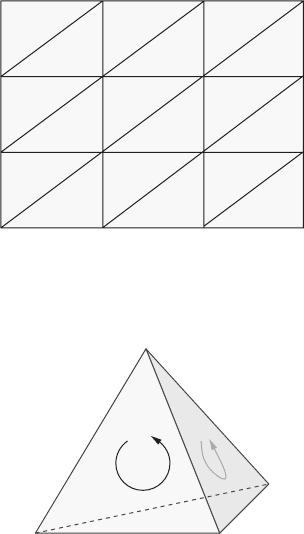
Figure 13.2 A triangulation of the 2-torus. (a) The torus as a rectangle with periodic boundary

conditions: the two edges labelled α will be glued together point-by-point along the arrows when

we reassemble the torus, and so are to be regarded as a single edge. The two sides labelled β will

be glued similarly. (b) The assembled torus: all four P’s are now in the same place, and correspond

to a single point.

(i) one is a face (or edge, or vertex) of the other;

(ii) the set of points in common is the whole of a shared face (or edge, or vertex).

The collection of simplices composing the dissected space is called a simplicial complex.

We will denote it by S.

We may not need many triangles to capture the global topology. For example,

Figure 13.2 shows how a two-dimensional torus can be decomposed into two 2-simplices

(triangles) bounded by three 1-simplices (edges) α, β, γ , and with only a single 0-simplex

(vertex) P. Computations are easier to describe, however, if each simplex in the decom-

position is uniquely specified by its vertices. For this, we usually need a slightly finer

dissection. Figure 13.3 shows a decomposition of the torus into 18 triangles, each of

which is uniquely labelled by three points drawn from a set of nine vertices. In this

figure vertices with identical labels are to be regarded as the same vertex, as are the

corresponding sides of triangles. Thus, each of the edges P

, P

at the top of

the figure are to be glued point-by-point to the corresponding edges on the bottom of the

figure; similarly along the sides. The resulting simplicial complex then has 27 edges.

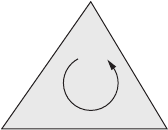
We may triangulate the sphere S

as a tetrahedron with vertices P

, P

. This

dissection has six edges: P

, P

, and four faces: P

, P

and P

(see Figure 13.4).

13.3 Homology 457

Figure 13.3 A second triangulation of the 2-torus.

Figure 13.4 A tetrahedral triangulation of the 2-sphere. The circulating arrows on the faces

indicate the choice of orientation P

and P

p-chains

We assign to simplices an orientation defined by the order in which we write their

defining vertices. The interchange of any pair of vertices reverses the orientation, and

we consider there to be a relative minus sign between oppositely oriented but otherwise

identical simplices: P

=−P

We now construct abstract vector spaces C

(S, R) of p-chains which have oriented

p-simplices as their basis vectors. The most general elements of C

(S, R), with S being

the tetrahedral triangulation of the sphere S

, would be

+ a

, (13.20)

where the coefficients a

, ..., a

are real numbers. We regard the distinct faces as being

linearly independent basis elements for C

(S, R). The space is therefore four dimen-

sional. If we had triangulated the sphere so that it had 16 triangular faces, the space C

would be 16 dimensional.

458 13 An introduction to differential topology

Similarly, the general element of C

(S, R) would be

+ b

, (13.21)

and so C

(S, R) is a six-dimensional space spanned by the edges of the tetrahedron. For

(S, R) we have

+ c

, (13.22)

and so C

(S, R) is four dimensional, and spanned by the vertices. Our manifold comprises

only the surface of the 2-sphere, so there is no such thing as C

(S, R).

The reason for making the field R explicit in these definitions is that we sometimes

gain more information about the topology if we allow only integer coefficients. The

space of such p-chains is then denoted by C

(S, Z). Because a vector space requires that

coefficients be drawn from a field, these objects are no longer vector spaces. They can

be thought of as either modules – “vector spaces” whose coefficients are drawn from a

ring – or as additive abelian groups.

The boundary operator

We now introduce a linear map ∂

: C

→ C

p−1

, called the boundary operator. Its

action on a p-simplex is

∂

···P

p+1



j=1

(−1)

j−1

...

...P

p+1

, (13.23)

where the “hat” indicates that P

is to be omitted. The resulting (p − 1)-chain is called

the boundary of the simplex. For example (see Figure 13.5)

∂

) = P

− P

+ P

= P

+ P

. (13.24)

The boundary of a line segment is the difference of its endpoints

∂

) = P

− P

. (13.25)

Figure 13.5 The oriented triangle P

has boundary P

+ P

13.3 Homology 459

Figure 13.6 Compatibly oriented simplices.

Finally, for any point,

∂

= 0. (13.26)

Because ∂

is defined to be a linear map, when it is applied to a p-chain c = a

···+a

, where the s

are p -simplices, we have ∂

c = a

∂

+···+a

∂

When we take the “∂” of a chain of compatibly oriented simplices that together make

up some region, the internal boundaries cancel in pairs, and the “boundary” of the chain

really is the oriented geometric boundary of the region. For example, in Figure 13.6 we

find that

∂(P

+ P

) = P

+ P

(13.27)

which is the anticlockwise directed boundary of the square.

For each of the examples above, we find that ∂

p−1

∂

s = 0. From the definition (13.23)

we can easily establish that this identity holds for any p-simplex s. As chains are sums

of simplices and ∂

is linear, it remains true for any c ∈ C

. Thus ∂

p−1

∂

= 0. We will

usually abbreviate this statement as ∂

= 0.

Cycles, boundaries and homology

A chain complex is a doubly infinite sequence of spaces (these can be vector spaces,

modules, abelian groups, or many other mathematical objects) such as ..., C

−2

, C

−1

, C

..., together with structure-preserving maps

...

∂

p+1

→ C

∂

→ C

p−1

∂

p−1

→ C

p−2

∂

p−2

→ ..., (13.28)

possessing the property that ∂

p−1

∂

= 0. The finite sequence of C

’s that we con-

structed from our simplicial complex is an example of a chain complex where C

zero-dimensional for p < 0orp > d. Chain complexes are a useful tool in mathematics,

and the ideas that we explain in this section have many applications.

Given any chain complex we can define two important linear subspaces of each of

the C

’s. The first is the space Z

of p-cycles. This consists of those z ∈ C

such

460 13 An introduction to differential topology

that ∂

z = 0. The second is the space B

of p-boundaries, and consists of those b ∈

such that b = ∂

p+1

c for some c ∈ C

p+1

. Because ∂

= 0, the boundaries B

constitute a subspace of Z

. From these spaces we form the quotient space H

= Z

consisting of equivalence classes of p-cycles, where we deem z

and z

to be equivalent,

or homologous, if they differ by a boundary: z

= z

+ ∂c. We write the equivalence

class of cycles homologous to z

as [z

]. The space H

, or, more accurately, H

(R),is

called the p-th (simplicial) homology space of the chain complex. It becomes the p-th

homology group if R is replaced by the integers.

We can construct these homology spaces for any chain complex. When the chain com-

plex is derived from a simplicial complex decomposition of a manifold M a remarkable

thing happens. The spaces C

, Z

and B

all depend on the details of how the manifold M

has been dissected to form the simplicial complex S. The homology space H

, however,

is independent of the dissection. This is neither obvious nor easy to prove. We will rely

on examples to make it plausible. Granted this independence, we will write H

(M ),or

(M , R), so as to make it clear that H

is a property of M . The dimension b

of H

(M )

is called the p-th Betti number of the manifold:

def

= dim H

(M ). (13.29)

Example: The 2-sphere. For the tetrahedral dissection of the 2-sphere, any vertex is P

homologous to any other, as P

−P

= ∂(P

) and all P

belong to C

. Furthermore,

∂P

= 0, so H

) is one-dimensional. In general, the dimension of H

(M ) is the

number of disconnected pieces making up M. We will write H

) = R, regarding R

as the archetype of a one-dimensional vector space.

Now let us consider H

). We first find the space of 1-cycles Z

. An element of C

will be in Z

only if each vertex that is the beginning of an edge is also the end of an

edge, and that these edges have the same coefficient. Thus,

= P

+ P

is a cycle, as is

= P

+ P

These are both boundaries of faces of the tetrahedron. It should be fairly easy to convince

yourself that Z

is the space of linear combinations of these together with boundaries of

the other faces

= P

+ P

= P

+ P

Any three of these are linearly independent, and so Z

is three-dimensional. Because all of

the cycles are boundaries, every element of Z

is homologous to 0, and so H

) ={0}.

13.3 Homology 461





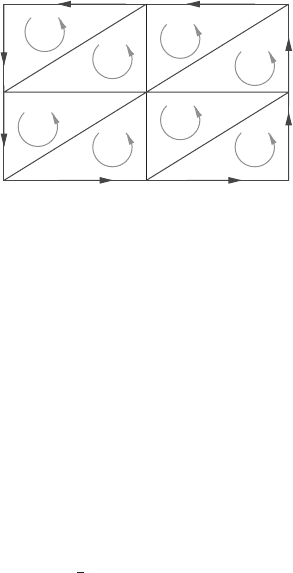
Figure 13.7 A basis of 1-cycles on the 2-torus.

We also see that H

) = R. Here the basis element is

− P

+ P

− P

, (13.30)

which is the 2-chain corresponding to the entire surface of the sphere. It would be the

boundary of the solid tetrahedron, but does not count as a boundary because the interior

of the tetrahedron is not part of the simplicial complex.

Example: The torus. Consider the 2-torus T

. We will see that H

) = R, H

) =

≡ R ⊕R and H

) = R. A natural basis for the two-dimensional H

) consists

of the 1-cycles α, β portrayed in Figure 13.7.

The cycle γ that, in Figure 13.2, winds once around the torus is homologous to α + β.

In terms of the second triangulation of the torus (Figure 13.3) we would have

α = P

+ P

β = P

+ P

, (13.31)

and

γ = P

+ P

= α + β + ∂(P

+ P

+···). (13.32)

Example: The projective plane. The projective plane RP

can be regarded as a rectangle

with diametrically opposite points identified. Suppose we decompose RP

into eight

triangles, as in Figure 13.8.

Consider the “entire surface”

σ = P

+ P

+···∈C

(RP

), (13.33)

consisting of the sum of all eight 2-simplices with the orientation indicated in the figure.

Let α = P

and β = P

be the sides of the rectangle running along

the bottom horizontal and left vertical sides of the figure, respectively. In each case they

462 13 An introduction to differential topology

Figure 13.8 A triangulation of the projective plane.

run from P

to P

. Then

∂(σ) = P

+ P

= 2(α − β) = 0. (13.34)

Although RP

has no actual edge that we can fall off, from the homological viewpoint

it does have a boundary! This represents the conflict between local orientation of each

of the 2-simplices and the global non-orientability of RP

. The surface σ of RP

is not

a two-cycle, therefore. Indeed Z

(RP

), and a fortiori H

(RP

), contain only the zero

vector. The only 1-cycle is α −β which runs from P

to P

via P

, P

and P

, but (13.34)

shows that this is the boundary of

σ . Thus H

(RP

, R) ={0} and H

(RP

, R) ={0},

while H

(RP

, R) = R.

We can now see the advantage of restricting ourselves to integer coefficients. When

we are not allowed fractions, the cycle γ = (α − β) is no longer a boundary, although

2(α − β) is the boundary of σ . Thus, using the symbol Z

to denote the additive group

of the integers modulo 2, we can write H

(RP

, Z) = Z

. This homology space is a set

with only two members {0γ ,1γ }. The finite group H

(RP

, Z) = Z

is said to be the

torsion part of the homology – a confusing terminology because this torsion has nothing

to do with the torsion tensor of Riemannian geometry.

We introduced real-number homology first, because the theory of vector spaces is

simpler than that of modules, and more familiar to physicists. The torsion is, however,

invisible to the real-number homology. We were therefore buying a simplification at the

expense of throwing away information.

The Euler character

The sum

χ(M )

def



p=0

(−1)

dim H

(M , R) (13.35)

13.3 Homology 463

is called the Euler character of the manifold M . For example, the 2-sphere has χ(S

) =

2, the projective plane has χ(RP

) = 1 and the n-torus has χ(T

) = 0. This number

is manifestly a topological invariant because the individual dim H

(M , R) are. We will

show that the Euler character is also equal to V −E +F −··· where V is the number of

vertices, E is the number of edges and F is the number of faces in the simplicial dissection.

The dots are for higher dimensional spaces, where the alternating sum continues with

(−1)

times the number of p-simplices. In other words, we are claiming that

χ(M ) =



p=0

(−1)

dim C

(M ). (13.36)

It is not so obvious that this new sum is a topological invariant. The individual dimensions

of the spaces of p-chains depend on the details of how we dissect M into simplices. If

our claim is to be correct, the dependence must somehow drop out when we take the

alternating sum.

Auseful tool for working with alternating sums of vector-space dimensions is provided

by the notion of an exact sequence. We say that a set of vector spaces V

with maps

: V

→ V

p+1

is an exact sequence if Ker (f

) = Im (f

p−1

). For example, if all

cycles were boundaries then the set of spaces C

with the maps ∂

taking us from

to C

p−1

would constitute an exact sequence – albeit with p decreasing rather than

increasing, but this is irrelevent. When the homology is non-zero, however, we only have

Im (f

p−1

) ⊂ Ker (f

), and the number dim H

= dim (Ker f

) − dim (Im f

p−1

) provides

a measure of how far this set inclusion falls short of being an equality.

Suppose that

{0}

−→ V

−→ ...

n−1

−→ V

−→ {0} (13.37)

is a finite-length exact sequence. Here, {0} is the vector space containing only the zero

vector. Being linear, f

maps 0 to 0. Also f

maps everything in V

to 0. Since this last

map takes everything to zero, and what is mapped to zero is the image of the penultimate

map, we have V

= Im f

n−1

. Similarly, the fact that Ker f

= Im f

={0} shows that

Im f

⊆ V

is an isomorphic image of V

. This situation is represented pictorially in

Figure 13.9.

Now the range–null-space theorem tells us that

dim V

= dim (Im f

) + dim (Ker f

)

= dim (Im f

) + dim (Im f

p−1

). (13.38)

When we take the alternating sum of the dimensions, and use dim (Im f

) = 0 and

dim (Im f

) = 0, we find that the sum telescopes to give



p=0

(−1)

dim V

= 0. (13.39)

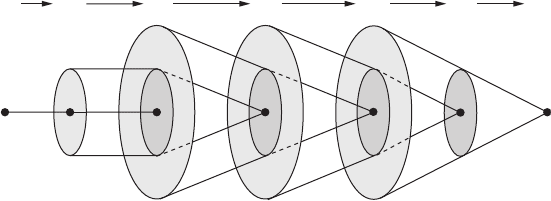
464 13 An introduction to differential topology

{ 0} { 0

}

000

Im f

Figure 13.9 A schematic representation of an exact sequence.

The vanishing of this alternating sum is one of the principal properties of an exact

sequence.

Now, for our sequence of spaces C

with the maps ∂

: C

→ C

p−1

, we have

dim (Ker ∂

) = dim (Im ∂

p+1

) + dim H

. Using this and the range–null-space theorem

in the same manner as above, shows that



p=0

(−1)

dim C

(M ) =



p=0

(−1)

dim H

(M ). (13.40)

This confirms our claim.

Exercise 13.1: Count the number of vertices, edges and faces in the triangulation we

used to compute the homology groups of the real projective plane RP

. Verify that

V − E + F = 1, and that this is the same number that we get by evaluating

χ(RP

) = dim H

(RP

, R) − dim H

(RP

, R) + dim H

(RP

, R).

Exercise 13.2: Show that the sequence

{0}→V

→ W →{0}

of vector spaces being exact means that the map φ : V → W is one-to-one and onto,

and hence an isomorphism V

∼

W .

Exercise 13.3: Show that a short exact sequence

{0}→A

→ B

→ C →{0}

of vector spaces is just a sophisticated way of asserting that C

∼

B/A. More precisely,

show that the map i is injective (one-to-one), so A can be considered to be a subspace

of B. Then show that the map π is surjective (onto), and can be regarded as projecting

B onto the equivalence classes B/A.