Stone M., Goldbart P. Mathematics for Physics: A Guided Tour for Graduate Students

Подождите немного. Документ загружается.

13.5 Poincaré duality 475

1 111





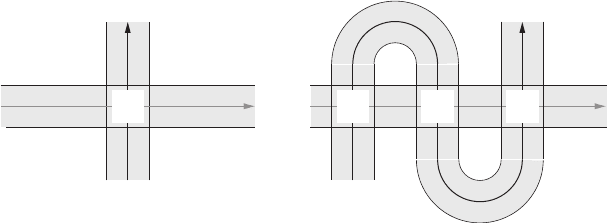
Figure 13.11 The intersection of two cycles: I (α, β) = 1 = 1 − 1 + 1.

both these forms being closed. The intersection number is given by the integral

I(α, β) =



∧ ω



f (x)f (y) dxdy = 1. (13.75)

The right-hand part of Figure 13.11 illustrates why this intersection number depends only

on the homology classes of the two 1-cycles, and not on their particular instantiation as

curves.

We can more conveniently re-express (13.72) in terms of the periods of the forms

def



f = I(i, k)f

, g

def



D−p

g = I(j, l)g

, (13.76)



f ∧ g =



i,j

K(i, j)



D−p

g, (13.77)

where

K(i, j) = I

−1

(i, k)I

−1

(j, l)I(k, l) = I

−1

(j, i) (13.78)

is the transpose of the inverse of the intersection-form matrix. The decomposition (13.77)

of the integral of the product of a pair of closed forms into a bilinear form in their periods

is one of the two principal results of this section, the other being (13.70).

In simple cases, we can obtain the decomposition (13.77) by more direct methods.

Suppose, for example, that we label the cycles generating the homology group H

)

of the 2-torus as α and β, and that a and b are closed (da = db = 0), but not necessarily

exact, 1-forms. We will show that



a ∧ b =



b −



a. (13.79)

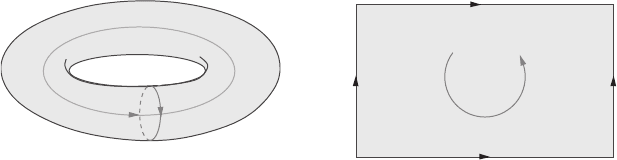
476 13 An introduction to differential topology







Figure 13.12 Cut-open torus.

To do this, we cut the torus along the cycles α and β and open it out into a rectangle with

sides of length L

and L

(see Figure 13.12). The cycles α and β will form the sides of

the rectangle, and we will take them as lying parallel to the x- and y-axes, respectively.

Functions on the torus now become functions on the rectangle. Not all functions on

the rectangle descend from functions on the torus, however. Only those functions that

satisfy the periodic boundary conditions f (0, y) = f (L

, y) and f (x,0) = f (x, L

) can

be considered (mathematicians would say “can be lifted”) to be functions on the torus.

Since the rectangle (but not the torus) is retractable, we can write a = df where f is a

function on the rectangle – but not necessarily a function on the torus, i.e. f will not, in

general, be periodic. Since a ∧ b = d(fb), we can now use Stokes’ theorem to evaluate



a ∧ b =



d(fb) =



∂T

fb. (13.80)

The two integrals on the two vertical sides of the rectangle can be combined to a single

integral over the points of the 1-cycle β:



vertical

fb =



[f (L

, y) − f (0, y)]b. (13.81)

We now observe that [f (L

, y) − f (0, y)] is a constant, and so can be taken out of the

integral. It is a constant because all paths from the point (0, y) to (L

, y) are homologous

to the one-cycle α, so the difference f (L

, y) − f (0, y) is equal to



a. Thus,



[f (L

, y) − f (0, y)]b =



b. (13.82)

Similarly, the contribution of the two horizontal sides is



[f (x,0) − f ((x, L

)]b =−



b. (13.83)

On putting the contributions of both pairs of sides together, the claimed result follows.

13.6 Characteristic classes 477

13.6 Characteristic classes

A supply of elements of H

(M , R) and H

(M , Z) is provided by the characteristic

classes associated with connections on vector bundles over the manifold M .

Recall that connections appear in covariant derivatives

∇

def

= ∂

+ A

, (13.84)

and are to be thought of as matrix-valued one-forms A = A

. In the quantum

mechanics of charged particles the covariant derivative that appears in the Schrödinger

equation is

∇

∂

∂x

− ieA

Maxwell

. (13.85)

Here, e is the charge of the particle on whose wavefunction the derivative acts, and

Maxwell

is the usual electromagnetic vector potential. The matrix-valued connection

1-form is therefore

A =−ieA

Maxwell

. (13.86)

In this case the matrix is one-by-one.

In a non-abelian gauge theory with gauge group G the connection becomes

A = i

. (13.87)

The

are hermitian matrices that have commutation relations [

]=if

, where

the f

are the structure constants of the Lie algebra of the group G. The

therefore

form a representation of the Lie algebra, and this representation plays the role of the

“charge” of the non-abelian gauge particle.

For covariant derivatives acting on a tangent vector field f

on a Riemann

n-manifold, where the e

are an orthonormal vielbein frame, we have

A = ω

abµ

, (13.88)

where, for each µ, the coefficients ω

abµ

=−ω

baµ

can be thought of as the entries in a

skew symmetric n-by-n matrix. These matrices are elements of the Lie algebra o(n) of

the orthogonal group O(n).

In all these cases we define the curvature two-form to be F = dA + A

, where

a combined matrix and wedge product is to be understood in A

. In Exercises 11.19

and 11.20 you used the Bianchi identity to show that the gauge-invariant 2n-forms

tr (F

) were closed. The integrals of these forms over cycles provide numbers that are

topological invariants of the bundle. For example, in four-dimensional QCD, the integral

=−

8π





tr (F

) (13.89)

478 13 An introduction to differential topology

over a compactified four-dimensional manifold  is an integer that a mathematician

would call the second Chern number of the non-abelian gauge bundle, and that a physicist

would call the instanton number of the gauge field configuration. The closed forms

themselves are called characteristic classes.

In the following section we will show that the integrals of characteristic classes are

indeed topological invariants. We also explain something of what these invariants are

measuring, and illustrate why, when suitably normalized, they are integer-valued.

13.6.1 Topological invariance

Suppose that we have been given a connection A and slightly deform it A → A + δA.

Then F → F + δF where

δF = d(δA) + δAA+ A δA. (13.90)

Using the Bianchi identity dF = FA − AF, we find that

δ tr(F

) = n tr(δFF

n−1

)

= n tr(d(δA)F

n−1

) + n tr(δAAF

n−1

) + n tr(A δAF

n−1

)

= n tr(d(δA)F

n−1

) + n tr(δAAF

n−1

) − n tr(δAF

n−1

= d



n tr(δAF

n−1

)



. (13.91)

The last line of (13.91) is equal to the penultimate line because all but the first and

last terms arising from the dF’s in d



tr(δAF

n−1

)



cancel in pairs. A globally defined

change in A therefore changes tr(F

) by the d of something, and so does not change its

cohomology class, or its integral over a cycle.

At first sight, this invariance under deformation suggests that all the tr(F

) are exact

forms – they can apparently all be written as tr(F

) = dω

2n−1

(A) for some (2n−1)-form

2n−1

(A). To find ω

2n−1

(A) all we have to do is deform the connection to zero by setting

= tAand

= dA

+ A

= tdA + t

. (13.92)

Then δA

= Aδt, and

tr(F

) = d



n tr(AF

n−1

)



. (13.93)

Integrating up from t = 0, we find

tr(F

) = d





tr(AF

n−1

) dt



. (13.94)

13.6 Characteristic classes 479

For example

tr(F

) = d





tr(A(tdA + t

) dt



= d





AdA +



. (13.95)

You should recognize here the ω

(A) = tr(AdA +

) Chern–Simons form of Exer-

cise 11.19. The naïve conclusion – that all the tr(F

) are exact – is false, however. What

the computation actually shows is that when



tr(F

) = 0 we cannot find a globally

defined 1-form A representing the connection or gauge field. With no global A, we cannot

globally deform A to zero.

Consider, for example, an abelian U(1) gauge field on the 2-sphere S

. When the first

Chern number

2πi



F (13.96)

is non-zero, there can be no globally defined 1-form A such that F = dA. Glance back,

however, at Figure 13.10 on page 472. There we see that the retractability of the spherical

caps D

guarantees that there are 1-forms A

defined on D

such that F = dA

in D

In the cingular region D

∩D

−

where they are both defined, A

and A

−

will be related

by a gauge transformation. For a U(1) gauge field, the matrix g appearing in the general

gauge transformation rule

A → A

≡ g

−1

Ag + g

−1

dg (13.97)

of Exercise 11.20 becomes the phase e

iχ

∈ U(1). Consequently

= A

−

+ e

−iχ

iχ

= A

−

+ idχ in D

∩ D

−

. (13.98)

The U(1) group element e

iχ

is required to be single valued in D

∩D

−

, but the angle χ

may be multivalued. We now write c

as the sum of integrals over the north and south

hemispheres of S

, and use Stokes’ theorem to reduce this sum to a single integral over

the hemispheres’ common boundary, the equator :

2πi



north

F +

2πi



south

2πi



north

2πi



south

−

2πi





−

2πi





−

2π





dχ . (13.99)

480 13 An introduction to differential topology

We see that c

is an integer that counts the winding of χ as we circle . Anon-zero integer

cannot be continuously reduced to zero, and if we attempt to deform A → tA → 0, we

will violate the required single-valuedness of the U(1) group element e

iχ

Although the Chern–Simons forms ω

2n−1

(A) cannot be defined globally, they are still

very useful in physics. They occur as Wess–Zumino terms describing the low-energy

properties of various quantum field theories, the prototype being the Skyrme–Witten

model of hadrons.

13.6.2 Chern characters and Chern classes

Any gauge-invariant polynomial (with exterior multiplication of forms understood) in

F provides a closed, topologically invariant, differential form. Certain combinations,

however, have additional desirable properties, and so have been given names.

The form

(F) = tr





2π





(13.100)

is called the n-th Chern character. It is convenient to think of this 2n-form as being the

n-th term in a generating-function expansion

ch(F)

def

= tr



exp



2π



= ch

(F) + ch

(F) +···, (13.101)

where ch

(F)

def

= tr I is the dimension of the space on which the

act. This formal sum

of forms of different degree is called the total Chern character. The n! normalization

is chosen because it makes the Chern character behave nicely when we combine vector

bundles – as we now do.

Given two vector bundles over the same manifold, having fibres U

and V

over the

point x, we can make a new bundle with the direct sum U

⊕ V

as fibre over x. This

resulting bundle is called the Whitney sum of the bundles. Similarly we can make a

tensor-product bundle whose fibre over x is U

⊗ V

Let us use the notation ch(U ) to represent the Chern character of the bundle with

fibres U

, and U ⊕ V to denote the Whitney sum. Then we have

ch(U ⊕ V ) = ch(U ) + ch(V ), (13.102)

and

ch(U ⊗ V ) = ch(U ) ∧ ch(V ). (13.103)

The second of these formulæ comes about because if

(1)

is a Lie algebra element acting

on V

(1)

and

(2)

the corresponding element acting on V

(2)

, then they act on the tensor

E. Witten, Nucl. Phys., B223 (1983) 422; ibid. B223 (1983) 433.

13.6 Characteristic classes 481

product V

(1)

⊗ V

(2)

(1⊗2)

(1)

⊗ I + I ⊗

(2)

, (13.104)

where I is the identity operator on the appropriate space in the tensor product, and for

matrices A and B we have

{

exp

(

A ⊗ I + I ⊗ B

)

}

= tr

{

exp A ⊗ exp B

}

= tr

{

exp A

}

{

exp B

}

. (13.105)

In terms of the individual ch

(V ), Equations (13.102) and (13.103) read

(U ⊕ V ) = ch

(U ) + ch

(V ), (13.106)

and

(U ⊗ V ) =



m=0

n−m

(U ) ∧ ch

(V ). (13.107)

Related to the Chern characters are the Chern classes. These are wedge-product

polynomials in the Chern characters, and are defined, via the matrix expansion

det (I + A) = 1 + tr A +



(tr A)

− tr A

+ ..., (13.108)

by the generating function for the total Chern class:

c(F) = det



I +

2π



= 1 + c

(F) + c

(F) +···. (13.109)

Thus

(F) = ch

(F), c

(F) =

(F) ∧ ch

(F) − ch

(F), (13.110)

and so on.

For matrices A and B we have det(A ⊕ B) = det(A) det(B), and this leads to

c(U ⊕V ) = c(U ) ∧ c(V ). (13.111)

Although the Chern classes are more complicated in appearance than the Chern char-

acters, they are introduced because their integrals over cycles turn out to be integers,

and this property remains true of integer-coefficient sums of products of Chern classes.

The cohomology classes [c

(F)] are therefore elements of the integer cohomology ring

•

(M , Z). This property does not hold for the Chern characters, whose integrals over

cycles can be fractions. The cohomology classes [ch

(F)] are therefore only elements

of H

•

(M , Q).

482 13 An introduction to differential topology

When we integrate products of Chern classes of total degree 2m over closed 2m-

dimensional orientable manifolds we get integer Chern numbers. These integers can

be related to generalized winding numbers, and characterize the extent to which the

gauge transformations that relate the connection fields in different patches serve to twist

the vector bundle. Unfortunately it requires a considerable amount of combinatorial

machinery (the Schubert calculus of complex Grassmannians) to explain these integers.

Pontryagin and Euler classes

When the fibres of a vector bundle are vector spaces over R, the complex skew-hermitian

matrices i

are replaced by real skew symmetric matrices. The Lie algebra of the n-

by-n matrices i

was a subalgebra of u(n). The Lie algebra of the n-by-n real, skew

symmetric, matrices is a subalgebra of o(n). Now, the trace of an odd power of any

skew symmetric matrix is zero. As a consequence, Chern characters and Chern classes

containing an odd number of F’s all vanish. The remaining real 4n-forms are known as

Pontryagin classes. The precise definition is

(V )

def

= (−1)

(V ). (13.112)

Pontryagin classes help to classify bundles whose gauge transformations are elements

of O(n). If we restrict ourselves to gauge transformations that lie in SO(n),aswe

would when considering the tangent bundle of an orientable Riemann manifold, then

we can make a gauge-invariant polynomial out of the skew-symmetric matrix-valued F

by forming its Pfaffian.

Recall (or see Exercise A.18) that the Pfaffian of a skew symmetric 2n-by-2n matrix

A with entries a

Pf A =



,...i

···a

2n−1

. (13.113)

The Euler class of the tangent bundle of a 2n-dimensional orientable manifold is defined

via its skew-symmetric Riemann-curvature form

R =

ab,µν

(13.114)

to be

e(R) = Pf



2π



. (13.115)

In four dimensions, for example, this becomes the 4-form

e(R) =

32π



abcd

. (13.116)

13.7 Hodge theory and the Morse index 483

The generalized Gauss–Bonnet theorem asserts – for an oriented, even-dimensional,

manifold without boundary – that the Euler character is given by

χ(M ) =



e(R). (13.117)

We will not prove this theorem, but in Section 16.3.6 we will illustrate the strategy that

leads to Chern’s influential proof.

Exercise 13.5: Show that

(F) =



(ch

(F))

− 6ch

(F)ch

(F) + 12 ch

(F)

13.7 Hodge theory and the Morse index

The Laplacian, when acting on a scalar function φ in R

, is simply div (grad φ), but

when acting on a vector v it becomes

∇

v = grad (div v) − curl (curl v). (13.118)

Why this weird expression? How should the Laplacian act on other types of fields?

For general curvilinear coordinates in R

, a reasonable definition for the Laplacian

of a vector or tensor field T is ∇

T = g

µν

∇

T, where ∇

is the flat-space covariant

derivative. This is the unique coordinate-independent object that reduces in cartesian

coordinates to the ordinary Laplacian acting on the individual components of T. The

proof that the rather different-seeming (13.118) holds for vectors is that it too is con-

structed out of coordinate-independent operations, and in cartesian coordinates reduces

to the ordinary Laplacian acting on the individual components of v. It must therefore

coincide with the covariant derivative definition. Why it should work out this way is

not exactly obvious. Now, div, grad and curl can all be expressed in differential-form

language, and therefore so can the scalar and vector Laplacian. Moreover, when we

let the Laplacian act on any p-form the general pattern becomes clear. The differential-

form definition of the Laplacian, and the exploration of its consequences, was the work

of William Hodge in the 1930s. His theory has natural applications to the topology of

manifolds.

13.7.1 The Laplacian on p-forms

Suppose that M is an oriented, compact, D-dimensional manifold without boundary. We

can make the space 

(M ) of p-form fields on M into an L

Hilbert space by introducing

the positive-definite inner product

a, b

=b, a



a  b =



√

...i

. (13.119)

484 13 An introduction to differential topology

Here, the subscript p denotes the order of the forms in the product, and should not be

confused with the p we have elsewhere used to label the norm in L

Banach spaces. The

presence of the

√

g and the Hodge  operator tells us that this inner product depends on

both the metric on M and the global orientation.

We can use this new inner product to define a “hermitian adjoint” δ ≡ d

†

of the exterior

differential operator d. The inverted commas “...” are because this hermitian adjoint is

not quite an adjoint operator in the normal sense – d takes us from one vector space to

another – but it is constructed in an analogous manner. We define δ by requiring that

da, b

p+1

=a, δb

, (13.120)

where a is an arbitrary p-form and b an arbitrary (p + 1)-form. Now recall that  takes

p-forms to (D −p) forms, and so d  b is a (D −p) form. Acting twice on a (D −p)-form

with  gives us back the original form multiplied by (−1)

p(D−p)

. We use this to compute

d(a  b) = da  b + (−1)

a(d  b)

= da  b + (−1)

(−1)

p(D−p)

a (d  b)

= da  b − (−1)

Dp+1

a (d  b). (13.121)

In obtaining the last line we have observed that p(p − 1) is an even integer and so

(−1)

p(1−p)

= 1. Now, using Stokes’ theorem, and the absence of a boundary to discard

the integrated-out part, we conclude that



(da)b = (−1)

Dp+1



a (d  b), (13.122)

da, b

p+1

= (−1)

Dp+1

a, ( d )b

(13.123)

and so δb = (−1)

Dp+1

( d )b. This was for δ acting on a (p − 1) form. Acting on a p

form instead we have

δ = (−1)

Dp+D+1

 d  . (13.124)

Observe how the sequence of maps in  d  works:



(M )



−→ 

D−p

(M )

−→ 

D−p+1

(M )



−→ 

p−1

(M ). (13.125)

The net effect is that δ takes a p-form to a (p−1)-form. Observe also that δ

∝  d

 = 0.