Stone M., Goldbart P. Mathematics for Physics: A Guided Tour for Graduate Students
Подождите немного. Документ загружается.

14.2 Representations 505
or g
1
H = g
2
H . The space X can therefore be identified with the space of cosets G/H .
Such sets are called quotient spaces or homogeneous spaces. Many spaces of significance
in physics can be thought of as cosets in this way.
Example: The rotation group SO(3) acts transitively on the 2-sphere S
2
. The SO(2)
subgroup of rotations about the z-axis leaves the north pole of the sphere fixed. We can
therefore identify S
2
* SO(3)/SO(2).
Many phase transitions are a result of spontaneous symmetry breaking. For example
the water → ice transition results in the continuous translation invariance of the liquid
water being broken down to the discrete translation invariance of the crystal lattice of
the solid ice. When a system with symmetry group G spontaneously breaks the sym-
metry to a subgroup H , the set of inequivalent ground states can be identified with the
homogeneous space G/H .
14.2 Representations
An n-dimensional representation of a group G is formally defined to be a homomorphism
from G to a subgroup of GL(n, C), the group of invertible n-by-n matrices with complex
entries. In effect, it is a set of n-by-n matrices that obey the group multiplication rules
D(g
1
)D(g
2
) = D(g
1
g
2
), D(g
−1
) =[D(g)]
−1
. (14.2)
Given such a representation, we can form another one D
(g) by conjugation with any
fixed invertible matrix C
D
(g) = C
−1
D(g)C. (14.3)
If D
(g) is obtained from D(g) in this way, we say that D and D
are equivalent repre-
sentations and write D ∼ D
. We can think of D and D
as being matrices representing
the same linear map, but in different bases. Our task in the rest of this chapter is to find
and classify all representations of a finite group G, up to equivalence.
Real and pseudo-real representations
We can form a new representation from D(g) by setting
D
(g) = D
∗
(g),
where D
∗
(g) denotes the matrix whose entries are the complex conjugates of those in
D(g). Suppose D
∗
∼ D. It may then be possible to find a basis in which the matrices
have only real entries. In this case we say the representation is real. It may be, however,
that D
∗
∼ D but we cannot find a basis in which the matrices become real. In this case
we say that D is pseudo-real.
506 14 Groups and group representations
Example: Consider the defining representation of SU(2) (the group of 2-by-2 unitary
matrices with unit determinant). Such matrices are necessarily of the form
U =
a −b
∗
ba
∗
, (14.4)
where a and b are complex numbers with |a|
2
+|b|
2
= 1. They are therefore specified
by three real parameters, and so the group manifold is three-dimensional. Now
a −b
∗
ba
∗
∗
=
a
∗
−b
b
∗
a
,
=
01
−10
a −b
∗
ba
∗
0 −1
10
,
=
0 −1
10
−1
a −b
∗
ba
∗
0 −1
10
, (14.5)
and so U ∼ U
∗
. It is not possible to find a basis in which all SU(2) matrices are
simultaneously real, however. If such a basis existed then, in that basis, a and b would
be real, and we could specify the matrices by only two real parameters – but we have
seen that we need three real numbers to describe all possible SU(2) matrices.
Direct sum and direct product
We can obtain new representations from old by combining them.
Given two representations D
(1)
(g) and D
(2)
(g), we can form their direct sum
D
(1)
⊕ D
(2)
as the set of block-diagonal matrices
D
(1)
(g) 0
0 D
(2)
(g)
. (14.6)
The dimension of this new representation is the sum of the dimensions of the two con-
stituent representations. We are particularly interested in taking a representation and
breaking it up as a direct sum of simpler representations.
Given two representations D
(1)
(g), D
(2)
(g), we can combine them in a different way
by taking their direct product D
(1)
⊗D
(2)
, which is the natural action of the group on the
tensor product of the representation spaces. In other words, if D
(1)
(g)e
(1)
j
= e
(1)
i
D
(1)
ij
(g)
and D
(2)
(g)e
(2)
j
= e
(2)
i
D
(2)
ij
(g), we define
[D
(1)
⊗ D
(2)
](g)(e
(1)
i
⊗ e
(2)
j
) = (e
(1)
k
⊗ e
(2)
l
)D
(1)
ki
(g)D
(2)
lj
(g). (14.7)
We think of D
(1)
ki
(g)D
(2)
lj
(g) being the entries in the direct-product matrix
[D
(1)
(g) ⊗ D
(2)
(g)]
kl,ij
,
14.2 Representations 507
whose rows and columns are indexed by pairs of numbers. The dimension of the product
representation is therefore the product of the dimensions of its factors.
Exercise 14.9: Show that if D(g) is a representation, then so is
D
(g) =[D(g
−1
)]
T
,
where the superscript T denotes the transposed matrix.
Exercise 14.10: Show that a map that assigns every element of a group G to the
1-by-1 identity matrix is a representation. It is, not unreasonably, called the trivial
representation.
Exercise 14.11: A representation D : G → GL(n, C) that assigns an element g ∈ G
to the n-by-n identity matrix I
n
if and only if g = e is said to be faithful. Let D be a
non-trivial, but non-faithful, representation of G by n-by-n matrices. Let H ⊂ G consist
of those elements h such that D(h) = I
n
. Show that H is a normal subgroup of G, and
that D descends to a faithful representation of the quotient group G/H .
Exercise 14.12: Let A and B be linear maps from U → U and let C and D be linear
maps from V → V . Then the direct products A ⊗ C and B ⊗ D are linear maps from
U ⊗ V → U ⊗ V . Show that
(A ⊗ C)(B ⊗ D) = (AB) ⊗ (CD).
Show also that
(A ⊕ C)(B ⊕ D) = (AB) ⊕ (CD).
Exercise 14.13: Let A and B be m-by-m and n-by-n matrices, respectively, and let I
n
denote the n-by-n unit matrix. Show that:
(i) tr(A ⊕ B) = tr(A) + tr(B).
(ii) tr(A ⊗ B) = tr(A) tr(B).
(iii) exp(A ⊕ B) = exp(A) ⊕ exp(B).
(iv) exp(A ⊗ I
n
+ I
m
⊗ B) = exp(A) ⊗ exp(B).
(v) det(A ⊕ B) = det(A) det(B).
(vi) det(A ⊗ B) = (det(A))
n
(det(B))
m
.
14.2.1 Reducibility and irreducibility
The “atoms” of representation theory are those representations that cannot, even by
a clever choice of basis, be decomposed into, or reduced to, a direct sum of smaller
representations. Such a representation is said to be irreducible. It is usually not easy to
tell just by looking at a representation whether it is reducible or not. To do this, we need
to develop some tools. We begin with a more powerful definition of irreducibility.
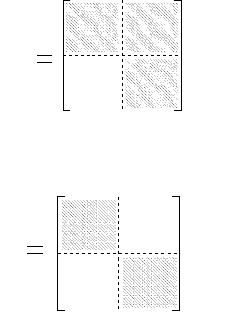
508 14 Groups and group representations
0
A
U
U
Figure 14.1 Block-partitioned reducible matrices.
0
0
A
U
U
Figure 14.2 Completely reducible matrices.
We first introduce the notion of an invariant subspace. Suppose we have a set {A
α
} of
linear maps acting on a vector space V . A subspace U ⊆ V is an invariant subspace for
the set if x ∈ U ⇒ A
α
x ∈ U for all A
α
. The set {A
α
} is irreducible if the only invariant
subspaces are V itself and {0}. Conversely, if there is a non-trivial invariant subspace,
then the set
4
of operators is reducible.
If the A
α
’s possess a non-trivial invariant subspace U , and we decompose V = U ⊕U
,
where U
is a complementary subspace, then, in a basis adapted to this decomposition,
the matrices A
α
take the block-partitioned form of Figure 14.1.
If we can find a
5
complementary subspace U
that is also invariant, then we have the
block partitioned form of Figure 14.2.
We say that such matrices are completely reducible. When our linear operators are
unitary with respect to some inner product, we can take the complementary subspace
to be the orthogonal complement. This, by unitarity, is automatically invariant. Thus,
unitarity and reducibility implies complete reducibility.
Schur’s lemma
The most useful results concerning irreducibility come from:
Schur’s lemma: Suppose we have two sets of linear operators A
α
: U → U , and B
α
:
V → V , that act irreducibly on their spaces, and an intertwining operator : U → V
such that
A
α
= B
α
, (14.8)
for all α. Then either
4
Irreducibility is a property of the set as a whole. Any individual matrix always has a non-trivial invariant
subspace because it possesses at least one eigenvector.
5
Remember that complementary subspaces are not unique.

14.2 Representations 509
(a) = 0,
or
(b) is one-to-one and onto (and hence invertible), in which case U and V have the
same dimension and A
α
=
−1
B
α
.
The proof is straightforward: The relation (14.8) shows that Ker () ⊆ U and Im() ⊆
V are invariant subspaces for the sets {A
α
} and {B
α
} respectively. Consequently, either
= 0, or Ker () ={0} and Im() = V . In the latter case is one-to-one and onto,
and hence invertible.
Corollary:If{A
α
} acts irreducibly on an n-dimensional vector space, and there is an
operator such that
A
α
= A
α
, (14.9)
then either = 0or = λI .
To see this, observe that (14.9) remains true if is replaced by ( − xI ). Now
det ( − xI ) is a polynomial in x of degree n, and, by the fundamental theorem of
algebra, has at least one root, x = λ. Since its determinant is zero, ( − λI) is not
invertible, and so must vanish by Schur’s lemma.
14.2.2 Characters and orthogonality
Unitary representations of finite groups
Let G be a finite group and let g (→ D(g) be a representation of G by matrices acting on a
vector space V . Let (x, y) denote a positive-definite, conjugate-symmetric, sesquilinear
inner product of two vectors in V . From ( , ) we construct a new inner product ,
by averaging over the group
x, y=
1
|G|
g∈G
(D(g)x, D(g)y). (14.10)
It is easy to see that this new inner product remains positive definite, and in addition has
the property that
D(g)x, D(g)y=x, y. (14.11)
This means that the maps D(g) : V → V are unitary with respect to the new product. If
we change basis to one that is orthonormal with respect to this new product, then the D(g)
become unitary matrices, with D(g
−1
) = D
−1
(g) = D
†
(g), where D
†
ij
(g) =[D
ji
(g)]
∗
denotes the conjugate-transposed matrix.
We conclude that representations of finite groups can always be taken to be unitary.
This leads to the important consequence that for such representations reducibility implies
complete reducibility.

510 14 Groups and group representations
Warning: In this construction it is essential that the sum over the g ∈ G converges.
This is guaranteed for a finite group, but may not work for infinite groups. In particular,
non-compact Lie groups, such as the Lorentz group, have no finite dimensional unitary
representations.
Orthogonality of the matrix elements
Now let D
J
(g) : V
J
→ V
J
be the matrices of an irreducible representation or irrep.
Here, J is a label that distinguishes inequivalent irreps from one another. We will use
the symbol dim J to denote the dimension of the representation vector space V
J
.
Let D
K
be an irrep that is either identical to D
J
or inequivalent to it, and let M
ij
be a
matrix possessing the appropriate number of rows and columns for the product D
J
MD
K
to be defined, but otherwise arbitrary. The sum
=
g∈G
D
J
(g
−1
)MD
K
(g) (14.12)
obeys D
J
(g) = D
K
(g) for any g. Consequently, Schur’s lemma tells us that
il
=
g∈G
D
J
ij
(g
−1
)M
jk
D
K
kl
(g) = λ(M )δ
il
δ
JK
. (14.13)
We are here summing over repeated indices, and have written λ(M ) to stress that the
number λ depends on the chosen matrix M . Now take M to be zero everywhere except
for one entry of unity in row j column k. Then we have
g∈G
D
J
ij
(g
−1
)D
K
kl
(g) = λ
jk
δ
il
, δ
JK
(14.14)
where we have relabelled λ to indicate its dependence on the location (j, k) of the non-
zero entry in M . We can find the constants λ
jk
by assuming that K = J , setting i = l
and summing over i. We find
|G|δ
jk
= λ
jk
dim J . (14.15)
Putting these results together we find that
1
|G|
g∈G
D
J
ij
(g
−1
)D
K
kl
(g) =
1
dim J
δ
jk
δ
il
δ
JK
. (14.16)
This matrix-element orthogonality theorem is often called the grand orthogonality
theorem because of its utility.
When our matrices D(g) are unitary, we can write the orthogonality theorem in a
slightly prettier form:
1
|G|
g∈G
D
J
ij
(g)
∗
D
K
kl
(g) =
1
dim J
δ
ik
δ
jl
δ
JK
. (14.17)

14.2 Representations 511
If we consider complex-valued functions G → C as forming a vector space, then the
individual matrix entries D
J
ij
are elements of this space and this form shows that they are
mutually orthogonal with respect to the natural sesquilinear inner product.
There can be no more orthogonal functions on G than the dimension of the function
space itself, which is |G|. We therefore have a constraint
J
(
dim J
)
2
≤|G| (14.18)
that places a limit on how many inequivalent representations can exist. In fact, as you
will show later, the equality holds: the sum of the squares of the dimensions of the
inequivalent irreducible representations is equal to the order of G, and consequently the
matrix elements form a complete orthonormal set of functions on G.
Class functions and characters
Because
tr (C
−1
DC) = tr D, (14.19)
the trace of a representation matrix is the same for equivalent representations.
Furthermore, because
tr D(g
−1
1
gg
1
) = tr
D
−1
(g
1
)D(g)D(g
1
)
= tr D(g), (14.20)
the trace is the same for all group elements in a conjugacy class. The character,
χ(g)
def
= tr D(g), (14.21)
is therefore said to be a class function.
By taking the trace of the matrix-element orthogonality relation we see that the
characters χ
J
= tr D
J
of the irreducible representations obey
1
|G|
g∈G
χ
J
(g)
∗
χ
K
(g) =
1
|G|
i
d
i
χ
J
i
∗
χ
K
i
= δ
JK
, (14.22)
where d
i
is the number of elements in the i-th conjugacy class.
The completeness of the matrix elements as functions on G implies that the characters
form a complete orthonormal set of functions on the space of conjugacy classes equipped
with the inner product
χ
1
, χ
2
def
=
1
|G|
i
d
i
χ
1
i
∗
χ
2
i
. (14.23)

512 14 Groups and group representations
Table 14.2 Character table of S
4
.
Typical element and class size
S
4
(1) (12) (123) (1234) (12)(34)
Irrep 1 6 8 6 3
A
1
11 1 1 1
A
2
1 −11−11
E 20−10 2
T
1
31 0 −1 −1
T
2
3 −10 1 −1
Consequently there are exactly as many inequivalent irreducible representations as there
are conjugacy classes in the group.
Given a reducible representation, D(g), we can find out exactly which irreps J it
contains, and how many times, n
J
, they occur. We do this by forming the compound
character
χ(g) = tr D(g) (14.24)
and observing that if we can find a basis in which
D(g) = (D
1
(g) ⊕ D
1
(g) ⊕···)
A
BC D
n
1
terms
⊕(D
2
(g) ⊕ D
2
(g) ⊕···)
A
BC D
n
2
terms
⊕···, (14.25)
then
χ(g) = n
1
χ
1
(g) + n
2
χ
2
(g) +··· (14.26)
From this we find that the multiplicities are given by
n
J
=χ , χ
J
=
1
|G|
i
d
i
(
χ
i
)
∗
χ
J
i
. (14.27)
There are extensive tables of group characters. Table 14.2 shows, for example, the
characters of the group S
4
of permutations on four objects.
Since χ
J
(e) = dim J we see that the irreps A
1
and A
2
are one-dimensional, that E
is two-dimensional, and that T
1,2
are both three-dimensional. Also we confirm that the
sum of the squares of the dimensions
1 + 1 + 2
2
+ 3
2
+ 3
2
= 24 = 4!
is equal to the order of the group.

14.2 Representations 513
As a further illustration of how to read Table 14.2, let us verify the orthonormality of
the characters of the representations T
1
and T
2
. We have
χ
T
1
, χ
T
2
=
1
|G|
i
d
i
χ
T
1
i
∗
χ
T
2
i
=
1
24
[1·3·3 − 6·1·1 + 8·0·0 − 6·1·1 + 3·1 · 1]=0,
while
χ
T
1
, χ
T
1
=
1
|G|
i
d
i
χ
T
1
i
∗
χ
T
1
i
=
1
24
[1·3·3 + 6·1·1 + 8·0·0 + 6·1·1 + 3·1·1]=1.
The sum giving χ
T
2
, χ
T
2
=1 is identical to this.
Exercise 14.14: Let D
1
and D
2
be representations with characters χ
1
(g) and χ
2
(g)
respectively. Show that the character of the direct product representation D
1
⊗ D
2
is
given by
χ
1⊗2
(g) = χ
1
(g)χ
2
(g).
14.2.3 The group algebra
Given a finite group G, we construct a vector space C(G) whose basis vectors are
in one-to-one correspondence with the elements of the group. We denote the vector
corresponding to the group element g by the boldface symbol g. A general element of
C(G) is therefore a formal sum
x = x
1
g
1
+ x
2
g
2
+···+x
|G|
g
|G|
. (14.28)
We take products of these sums by using the group multiplication rule. If g
1
g
2
= g
3
we
set g
1
g
2
= g
3
, and require the product to be distributive with respect to vector-space
addition. Thus
gx = x
1
gg
1
+ x
2
gg
2
+···+x
|G|
gg
|G|
. (14.29)
The resulting mathematical structure is called the group algebra. It was introduced by
Frobenius.
The group algebra, considered as a vector space, is automatically a representation. We
define the natural action of G on C(G) by setting
D(g)g
i
= gg
i
= g
j
D
ji
(g). (14.30)
The matrices D
ji
(g) make up the regular representation. Because the list gg
1
, gg
2
, ...
is a permutation of the list g
1
, g
2
, ..., their matrix entries consist of 1’s and 0’s, with
exactly one non-zero entry in each row and each column.
514 14 Groups and group representations
Exercise 14.15: Show that the character of the regular representation has χ(e) =|G|,
and χ(g) = 0, for g = e.
Exercise 14.16: Use the previous exercise to show that the number of times an
n-dimensional irrep occurs in the regular representation is n. Deduce that |G|=
,
J
(dim J )
2
, and from this construct the completeness proof for the representations
and characters.
Projection operators
A representation D
J
of the group G automatically provides a representation of the group
algebra. We simply set
D
J
(x
1
g
1
+ x
2
g
2
+···)
def
= x
1
D
J
(g
1
) + x
2
D
J
(g
2
) +···. (14.31)
Certain linear combinations of group elements turn out to be very useful because the
corresponding matrices can be used to project out vectors possessing desirable symmetry
properties.
Consider the elements
e
J
αβ
=
dim J
|G|
g∈G
7
D
J
αβ
(g)
8
∗
g (14.32)
of the group algebra. These have the property that
g
1
e
J
αβ
=
dim J
|G|
g∈G
7
D
J
αβ
(g)
8
∗
(g
1
g)
=
dim J
|G|
g∈G
7
D
J
αβ
(g
−1
1
g)
8
∗
g
=
7
D
J
αγ
(g
−1
1
)
8
∗
dim J
|G|
g∈G
7
D
J
γβ
(g)
8
∗
g
= e
J
γβ
D
J
γα
(g
1
). (14.33)
In going from the first to the second line we have changed summation variables from
g → g
−1
1
g, and in going from the second to the third line we have used the representation
property to write D
J
(g
−1
1
g) = D
J
(g
−1
1
)D
J
(g).
