Stone M., Goldbart P. Mathematics for Physics: A Guided Tour for Graduate Students
Подождите немного. Документ загружается.


14.2 Representations 515
From g
1
e
J
αβ
= e
J
γβ
D
J
γα
(g
1
) and the matrix-element orthogonality, it follows that
e
J
αβ
e
K
γδ
=
dim J
|G|
g∈G
7
D
J
αβ
(g)
8
∗
ge
K
γδ
=
dim J
|G|
g∈G
7
D
J
αβ
(g)
8
∗
D
K
γ
(g)e
K
δ
= δ
JK
δ
α
δ
βγ
e
K
δ
= δ
JK
δ
βγ
e
J
αδ
. (14.34)
For each J , this multiplication rule of the e
J
αβ
is identical to that of matrices having zero
entries everywhere except for the (α, β)-th, which is a “1”. There are (dim J )
2
of these
e
J
αβ
for each n-dimensional representation J , and they are linearly independent. Because
,
J
(dim J )
2
=|G|, they form a basis for the algebra. In particular every element of G
can be reconstructed as
g =
J
D
J
ij
(g)e
J
ij
. (14.35)
We can also define the useful objects
P
J
=
i
e
J
ii
=
dim J
|G|
g∈G
7
χ
J
(g)
8
∗
g. (14.36)
They have the property
P
J
P
K
= δ
JK
P
K
,
J
P
J
= I, (14.37)
where I is the identity element of C(G). The P
J
are therefore projection operators
composing a resolution of the identity. Their utility resides in the fact that when D(g) is
a reducible representation acting on a linear space
V =
G
J
V
J
, (14.38)
then setting g → D(g) in the formula for P
J
results in a projection matrix from V onto
the irreducible component V
J
. To see how this comes about, let v ∈ V and, for any fixed
p, set
v
i
= e
J
ip
v, (14.39)
where e
J
ip
v should be understood as shorthand for D(e
J
ip
)v. Then
D(g)v
i
= ge
J
ip
v = e
J
jp
vD
J
ji
(g) = v
j
D
J
ji
(g). (14.40)

516 14 Groups and group representations
We see that the v
i
, if not all zero, are basis vectors for V
J
. Since P
J
is a sum of the
e
J
ij
, the vector P
J
v is a sum of such vectors, and therefore lies in V
J
. The advantage of
using P
J
over any individual e
J
ip
is that P
J
can be computed from character tables, i.e.
its construction does not require knowledge of the irreducible representation matrices.
The algebra of classes
If a conjugacy class C
i
consists of the elements {g
1
, g
2
, ...g
d
i
}, we can define C
i
to be
the corresponding element of the group algebra:
C
i
=
1
d
i
(g
1
+ g
2
+···g
d
i
). (14.41)
(The factor of 1/d
i
is a conventional normalization.) Because conjugation merely per-
mutes the elements of a conjugacy class, we have g
−1
C
i
g = C
i
for all g ∈ C(G).
The C
i
therefore commute with every element of C(G ). Conversely any element
of C(G) that commutes with every element in C(G) must be a linear combination:
C = c
1
C
1
+ c
2
C
2
+ ... The subspace of C(G) consisting of sums of the classes is
therefore the centre Z[C(G)] of the group algebra. Because the product C
i
C
j
commutes
with every element, it lies in Z[C(G)], and so there are constants c
ij
k
such that
C
i
C
j
=
k
c
ij
k
C
k
. (14.42)
We can regard the C
i
as being linear maps from Z[C(G)] to itself, whose associated
matrices have entries (C
i
)
k
j
= c
ij
k
. These matrices commute, and can be simultaneously
diagonalized. We will leave it as an exercise for the reader to demonstrate that
C
i
P
J
=
χ
J
i
χ
J
0
P
J
. (14.43)
Here χ
J
0
≡ χ
J
{e}
= dim J . The common eigenvectors of the C
i
are therefore the pro-
jection operators P
J
, and the eigenvalues λ
J
i
= χ
J
i
/χ
J
0
are, up to normalization, the
characters. Equation (14.43) provides a convenient method for computing the characters
from knowledge only of the coefficients c
ij
k
appearing in the class multiplication table.
Once we have found the eigenvalues λ
J
i
, we recover the χ
J
i
by noting that χ
J
0
is real and
positive, and that
,
i
d
i
|χ
J
i
|
2
=|G|.
Exercise 14.17: Use Schur’s lemma to show that for an irrep D
J
(g) we have
1
d
i
g∈C
i
D
J
jk
(g) =
1
dim J
δ
jk
χ
J
i
,
and hence establish (14.43).

14.3 Physics applications 517
14.3 Physics applications
14.3.1 Quantum mechanics
When a group G ={g
i
} acts on a mechanical system, then G will act as a set of linear
operators D(g) on the Hilbert space H of the corresponding quantum system. Thus H
will be a representation
6
space for G. If the group is a symmetry of the system then the
D(g) will commute with the Hamiltonian
ˆ
H . If this is so, and if we can decompose
H =
G
irreps J
H
J
(14.44)
into
ˆ
H -invariant irreps of G then Schur’s lemma tells us that in each H
J
the Hamiltonian
ˆ
H will act as a multiple of the identity operator. In other words every state in H
J
will
be an eigenstate of
ˆ
H with a common energy E
J
.
This fact can greatly simplify the task of finding the energy levels. If an irrep J
occurs only once in the decomposition of H then we can find the eigenstates directly by
applying the projection operator P
J
to vectors in H. If the irrep occurs n
J
times in the
decomposition, then P
J
will project to the reducible subspace
H
J
⊕ H
J
⊕···H
J
A BC D
n
J
copies
= M ⊗ H
J
.
Here M is an n
J
-dimensional multiplicity space. The Hamiltonian
ˆ
H will act in M as
an n
J
-by-n
J
matrix. In other words, if the vectors
|n, i≡|n⊗|i∈M ⊗ H
J
(14.45)
form a basis for M ⊗H
J
, with n labelling which copy of H
J
the vector |n, ilies in, then
ˆ
H |n, i=|m, iH
J
mn
,
D(g)|n, i=|n, jD
J
ji
(g). (14.46)
Diagonalizing H
J
nm
provides us with n
j
ˆ
H -invariant copies of H
J
and gives us the energy
eigenstates.
Consider, for example, the molecule C
60
(buckminsterfullerene) consisting of 60
carbon atoms in the form of a soccer ball. The chemically active electrons can be treated
in a tight-binding approximation in which the Hilbert space has dimension 60 – one π -
orbital basis state for each carbon atom. The geometric symmetry group of the molecule
6
The rules of quantum mechanics only require that D(g
1
)D(g
2
) = e
iφ(g
1
,g
2
)
D(g
1
g
2
). A set of matrices that
obeys the group multiplication rule “up to a phase” is called a projective (or ray) representation. In many
cases, however, we can choose the D(g) so that φ is not needed. This is the case in all the examples we
discuss.

518 14 Groups and group representations
Table 14.3 Character table for the group Y .
Typical element and class size
YeC
5
C
2
5
C
2
C
3
Irrep 1 12 12 15 20
A 11111
T
1
3 τ
−1
−τ −10
T
2
3 −ττ
−1
−10
G 4 −1 −101
H 5001−1
1
2
3
0
g
g
h
u
h
g
g
g
L=4
t
g2
g
u
h
u
t
2u
h
g
t
1g
t
1u
g
u
t
2u
h
g
t
1u
a
g
L=3
L=2
L=1
L=0
–3
–2
–1
E
C
60
Figure 14.3 A sketch of the tight-binding electronic energy levels of C
60
.
is Y
h
= Y ×Z
2
, where Y is the rotational symmetry group of the icosahedron (a subgroup
of SO(3)) and Z
2
is the parity inversion σ : r (→−r. The characters of Y are displayed
in Table 14.3. In this table τ =
1
2
(
√
5 − 1) denotes the golden mean. The class C
5
is the set of 2π/5 rotations about an axis through the centres of a pair of antipodal
pentagonal faces, the class C
3
is the set of of 2π/3 rotations about an axis through the
centres of a pair of antipodal hexagonal faces and C
2
is the set of π rotations through the
midpoints of a pair of antipodal edges, each lying between two adjacent hexagonal faces.
The geometric symmetry group acts on the 60-dimensional Hilbert space by permuting
the basis states concurrently with their associated atoms. Figure 14.3 shows how the
60 states are disposed into energy levels.
7
Each level is labelled by a lower-case letter
specifying the irrep of Y , and by a subscript g or u standing for gerade (German for
7
After R. C. Haddon, L. E. Brus, K. Raghavachari, Chem. Phys. Lett., 125 (1986) 459.

14.3 Physics applications 519
even)orungerade (German for odd) that indicates whether the wavefunction is even or
odd under the inversion σ : r (→−r.
The buckyball is roughly spherical, and the lowest 25 states can be thought of as being
derived from the L = 0, 1, 2, 3, 4 eigenstates, where L is the angular momentum quantum
number that classifies the energy levels for an electron moving on a perfect sphere. In
the many-electron ground-state, the 30 single-particle states with energy below E < 0
are each occupied by pairs of spin up/down electrons. The 30 states with E > 0 are
empty.
To explain, for example, why three copies of T
1
appear, and why two of these are T
1u
and one T
1g
, we must investigate the manner in which the 60-dimensional Hilbert space
decomposes into irreducible representations of the 120-element group Y
h
. Problem 14.23
leads us through this computation, and shows that no irrep of Y
h
occurs more than three
times. In finding the energy levels, we therefore never have to diagonalize a matrix
bigger than 3-by-3.
The equality of the energies of the h
g
and g
g
levels at E =−1isanaccidental
degeneracy . It is not required by the symmetry, and will presumably disappear in a
more sophisticated calculation. The appearance of many “accidental” degeneracies in an
energy spectrum hints that there may be a hidden symmetry that arises from something
beyond geometry. For example, in the Schrödinger spectrum of the hydrogen atom all
states with the same principal quantum number n have the same energy although they
correspond to different irreps L = 1, ..., n −1ofO(3). This degeneracy occurs because
the classical Kepler-orbit problem has symmetry group O(4), rather than the naïvely
expected O(3) rotational symmetry.
14.3.2 Vibrational spectrum of H
2
O
The small vibrations of a mechanical system with n degrees of freedom are governed by
a Lagrangian of the form
L =
1
2
˙x
T
M ˙x −
1
2
x
T
V x (14.47)
where M and V are symmetric n-by-n matrices, and with M being positive definite. This
Lagrangian leads to the equations of motion
M ¨x = V x. (14.48)
We look for normal mode solutions x(t) ∝ e
iω
i
t
x
i
, where the vectors x
i
obey
−ω
2
i
M x
i
= V x
i
. (14.49)
The normal-mode frequencies are solutions of the secular equation
det (V − ω
2
M ) = 0, (14.50)
520 14 Groups and group representations
and modes with distinct frequencies are orthogonal with respect to the inner product
defined by M,
x, y=x
T
M y. (14.51)
We are interested in solving this problem for vibrations about the equilibrium config-
uration of a molecule. Suppose this equilibrium configuration has a symmetry group G.
This gives rise to an n-dimensional representation on the space of x’s in which
g : x (→ D(g)x (14.52)
leaves both the intertia matrix M and the potential matrix V unchanged:
[D(g)]
T
MD(g) = M , [D(g)]
T
VD(g) = V . (14.53)
Consequently, if we have an eigenvector x
i
with frequency ω
i
,
−ω
2
i
M x
i
= V x
i
(14.54)
we see that D(g)x
i
also satisfies this equation. The frequency eigenspaces are therefore
left invariant by the action of D(g) and, barring accidental degeneracy, there will be
a one-to-one correspondence between the frequency eigenspaces and the irreducible
representations occurring in D(g).
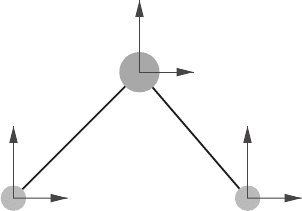
Consider, for example, the vibrational modes of the water molecule H
2
O (Figure 14.4).
This familiar molecule has symmetry group C
2v
which is generated by two elements: a
rotation a through π about an axis through the oxygen atom, and a reflection b in the
plane through the oxygen atom and bisecting the angle between the two hydrogens. The
product ab is a reflection in the plane defined by the equilibrium position of the three
atoms. The relations are a
2
= b
2
= (ab)
2
= e, and the characters are displayed in
Table 14.4.
The group C
2v
is abelian, so all the representations are one dimensional.
H
1
H
2
O
x
H
1
x
H
2
y
O
x
O
y
H
1
y
H
2
Figure 14.4 Water molecule.

14.3 Physics applications 521
Table 14.4 Character table of C
2v
.
Class and size
C
2v
eabab
Irrep1111
A
1
1111
A
2
11−1 −1
B
1
1 −11−1
B
2
1 −1 −11
To find out what representations occur when C
2v
acts, we need to find the character
of its action D(g) on the nine-dimensional vector
x = (x
O
, y
O
, z
O
, x
H
1
, y
H
1
, z
H
1
, x
H
2
, y
H
2
, z
H
2
). (14.55)
Here the coordinates x
H
2
, y
H
2
, z
H
2
etc. denote the displacements of the labelled atom
from its equilibrium position.
We take the molecule as lying in the xy-plane, with the z pointing towards us. The
effect of the symmetry operations on the atomic displacements is
D(a)x = (−x
O
, +y
O
, −z
O
, −x
H
2
, +y
H
2
, −z
H
2
, −x
H
1
, +y
H
1
, −z
H
1
),
D(b)x = (−x
O
, +y
O
, +z
O
, −x
H
2
, +y
H
2
, +z
H
2
, −x
H
1
, +y
H
1
, +z
H
1
),
D(ab)x = (+x
O
, +y
O
, −z
O
, +x
H
1
, +y
H
1
, −z
H
1
, +x
H
2
, +y
H
2
, −z
H
2
).
Notice how the transformations D(a), D(b) have interchanged the displacement coor-
dinates of the two hydrogen atoms. In calculating the character of a transformation we
need look only at the effect on atoms that are left fixed – those that are moved have
matrix elements only in non-diagonal positions. Thus, when computing the compound
characters for ab, we can focus on the oxygen atom. For ab we need to look at all three
atoms. We find
χ
D
(e) = 9,
χ
D
(a) =−1 + 1 − 1 =−1,
χ
D
(b) =−1 + 1 + 1 = 1,
χ
D
(ab) = 1 + 1 − 1 + 1 + 1 − 1 + 1 + 1 − 1 = 3.
By using the orthogonality relations, we find the decomposition
⎛
⎜
⎜
⎝
9
−1
1
3
⎞
⎟
⎟
⎠
= 3
⎛
⎜
⎜
⎝
1
1
1
1
⎞
⎟
⎟
⎠
+
⎛
⎜
⎜
⎝
1
1
−1
−1
⎞
⎟
⎟
⎠
+ 2
⎛
⎜
⎜
⎝
1
−1
1
−1
⎞
⎟
⎟
⎠
+ 3
⎛
⎜
⎜
⎝
1
−1
−1
1
⎞
⎟
⎟
⎠
(14.56)
522 14 Groups and group representations
or
χ
D
= 3χ
A
1
+ χ
A
2
+ 2χ
B
1
+ 3χ
B
2
. (14.57)
Thus, the nine-dimensional representation decomposes as
D = 3A
1
⊕ A
2
⊕ 2B
1
⊕ 3B
2
. (14.58)
How do we exploit this? First we cut out the junk. Out of the nine modes, six cor-
respond to easily identified zero-frequency motions – three of translation and three
rotations. A translation in the x-direction would have x
O
= x
H
1
= x
H
2
= ξ , all other
entries being zero. This displacement vector changes sign under both a and b, but is
left fixed by ab. This behaviour is characteristic of the representation B
2
. Similarly
we can identify A
1
as translation in y, and B
1
as translation in z. A rotation about the
y -axis makes z
H
1
=−z
H
2
= φ. This is left fixed by a, but changes sign under b
and ab, so the y rotation mode is A
2
. Similarly, rotations about the x- and z-axes cor-
respond to B
1
and B
2
, respectively. All that is left for genuine vibrational modes is
2A
1
⊕ B
2
.
We now apply the projection operator
P
A
1
=
1
4
[(χ
A
1
(e))
∗
D(e) + (χ
A
1
(a))
∗
D(b) + (χ
A
1
(b))
∗
D(b) + (χ
A
1
(ab))
∗
D(ab)]
(14.59)
to v
H
1
,x
, a small displacement of H
1
in the x-direction. We find
P
A
1
v
H
1
,x
=
1
4
(v
H
1
,x
− v
H
2
,x
− v
H
2
,x
+ v
H
1
,x
)
=
1
2
(v
H
1
,x
− v
H
2
,x
). (14.60)
This mode is an eigenvector for the vibration problem.
If we apply P
A
1
to v
H
1
,y
and v
O,y
we find
P
A
1
v
H
1
,y
=
1
2
(v
H
1
,y
+ v
H
2
,y
),
P
A
1
v
O,y
= v
O,y
, (14.61)
but we are not quite done. These modes are contaminated by the y translation direction
zero mode, which is also in an A
1
representation. After we make our modes orthogonal
to this, there is only one left, and this has y
H
1
= y
H
2
=−y
O
m
O
/(2m
H
) = a
1
, all other
components vanishing.

14.3 Physics applications 523
We can similarly find vectors corresponding to B
2
as
P
B
2
v
H
1
,x
=
1
2
(v
H
1
,x
+ v
H
2
,x
)
P
B
2
v
H
1
,y
=
1
2
(v
H
1
,y
− v
H
2
,y
)
P
B
2
v
O,x
= v
O,x
and these need to be cleared of both translations in the x-direction and rotations about
the z-axis, both of which transform under B
2
. Again there is only one mode left and it is
y
H
1
=−y
H
2
= αx
H
1
= αx
H
2
= βx
0
= a
2
(14.62)
where α is chosen to ensure that there is no angular momentum about O, and β to
make the total x linear momentum vanish. We have therefore found three true vibration
eigenmodes, two transforming under A
1
and one under B
2
as advertised earlier. The
eigenfrequencies, of course, depend on the details of the spring constants, but now that
we have the eigenvectors we can just plug them in to find these.
14.3.3 Crystal field splittings
A quantum mechanical system has a symmetry G if the Hamiltonian
ˆ
H obeys
D
−1
(g)
ˆ
HD(g) =
ˆ
H , (14.63)
for some group action D(g) : H → H on the Hilbert space. If follows that the
eigenspaces, H
λ
, of states with a common eigenvalue, λ, are invariant subspaces for the
representation D(g).
We often need to understand how a degeneracy is lifted by perturbations that break
G down to a smaller subgroup H .Ann-dimensional irreducible representation of G
is automatically a representation of any subgroup of G, but in general it is no longer
irreducible. Thus the n-fold degenerate level is split into multiplets, one for each of
the irreducible representations of H contained in the original representation. The man-
ner in which an originally irreducible representation decomposes under restriction to a
subgroup is known as the branching rule for the representation.
Aphysically important case is given by the breaking of the full SO(3) rotation symme-
try of an isolated atomic Hamiltonian by a crystal field. Suppose the crystal has octohedral
symmetry. The characters of the octohedral group are displayed in Table 14.5.
The classes are labelled by the rotation angles, C
2
being a twofold rotation axis
(θ = π ), C
3
a threefold axis (θ = 2π/3), etc.
The character of the J = l representation of SO(3) is
χ
l
(θ) =
sin(2l + 1)θ/2
sin θ/2
, (14.64)

524 14 Groups and group representations
Table 14.5 Character table of the octohedral group O.
Class (size)
OeC
3
(8) C
2
4
(3) C
2
(6) C
4
(6)
A
1
11111
A
2
11 1−1 −1
E 2 −1200
F
2
30−11−1
F
1
30−1 −11
Table 14.6 Characters evaluated on rotation classes.
Class (size)
leC
3
(8) C
2
4
(3) C
2
(6) C
4
(6)
011111
13 0 −1 −1 −1
25 −111−1
37 1 −1 −1 −1
490111
and the first few χ
l
’s evaluated on the rotation angles of the classes of O are dsiplayed
in Table 14.6.
The ninefold degenerate l = 4 multiplet therefore decomposes as
⎛
⎜
⎜
⎜
⎜
⎜
⎝
9
0
1
1
1
⎞
⎟
⎟
⎟
⎟
⎟
⎠
=
⎛
⎜
⎜
⎜
⎜
⎜
⎝
1
1
1
1
1
⎞
⎟
⎟
⎟
⎟
⎟
⎠
+
⎛
⎜
⎜
⎜
⎜
⎜
⎝
2
−1
2
0
0
⎞
⎟
⎟
⎟
⎟
⎟
⎠
+
⎛
⎜
⎜
⎜
⎜
⎜
⎝
3
0
−1
−1
1
⎞
⎟
⎟
⎟
⎟
⎟
⎠
+
⎛
⎜
⎜
⎜
⎜
⎜
⎝
3
0
−1
1
−1
⎞
⎟
⎟
⎟
⎟
⎟
⎠
, (14.65)
or
χ
4
SO(3)
= χ
A
1
+ χ
E
+ χ
F
1
+ χ
F
2
. (14.66)
The octohedral crystal field splits the nine states into four multiplets with symmetries
A
1
, E, F
1
, F
2
and degeneracies 1, 2, 3 and 3, respectively.
We have considered only the simplest case here, ignoring the complications introduced
by reflection symmetries, and by two-valued spinor representations of the rotation group.
