Stone M., Goldbart P. Mathematics for Physics: A Guided Tour for Graduate Students

Подождите немного. Документ загружается.

12.1 Basic notions 415

=1 2 3 4 5 6



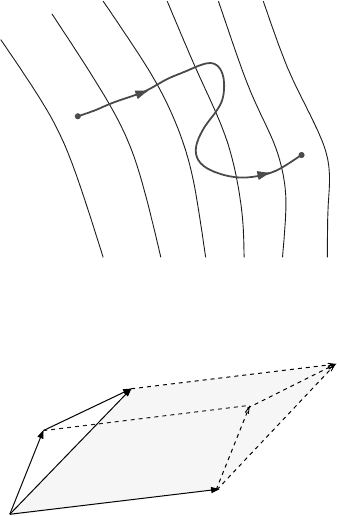
Figure 12.1 The integral of a 1-form.

Figure 12.2 Additivity of ω(x, y).

retrace our route, so that we pass over some part of  three times – twice forward and

once back – we obtain the same answer as if we went only forward.

12.1.2 Skew-symmetry and orientations

What about integrating 2- and 3-forms? Why the skew-symmetry? To answer these

questions, think about assigning some sort of “area” in R

to the parallelogram defined

by the two vectors x, y . This is going to be some function of the two vectors. Let us call

it ω(x , y). What properties do we demand of this function? There are at least three:

(i) Scaling: If we double the length of one of the vectors, we expect the area to double.

Generalizing this, we demand that ω(λx, µy) = (λµ)ω(x, y). (Note that we are

not putting modulus signs on the lengths, so we are allowing negative “areas”, and

allowing for the sign to change when we reverse the direction of a vector.)

(ii) Additivity: The drawing in Figure 12.2 shows that we ought to have

ω(x

+ x

, y) = ω(x

, y) + ω(x

, y), (12.4)

similarly for the second slots.

(iii) Degeneration: If the two sides coincide, the area should be zero. Thus ω(x, x ) = 0.

416 12 Integration on manifolds

The first two properties show that ω should be a multilinear form. The third shows

that it must be skew-symmetric:

0 = ω(x + y, x + y) = ω(x, x) + ω(x, y) + ω(y, x) + ω(y, y)

= ω(x, y) + ω(y, x). (12.5)

So we have

ω(x, y) =−ω(y, x). (12.6)

These are exactly the properties possessed by a 2-form. Similarly, a 3-form outputs a

volume element.

These volume elements are oriented. Remember that an orientation of a set of vectors

is a choice of order in which to write them. If we interchange two vectors, the orien-

tation changes sign. We do not distinguish orientations related by an even number of

interchanges. A p-form assigns a signed (±) p-dimensional volume element to an ori-

entated set of vectors. If we change the orientation, we change the sign of the volume

element.

Orientable and non-orientable manifolds

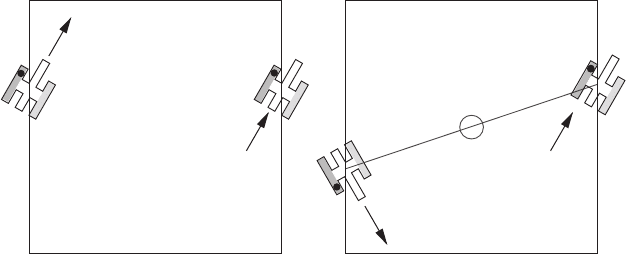
In the classic video game Asteroids, you could select periodic boundary conditions so

that your spaceship would leave the right-hand side of the screen and re-appear on the left

(Figure 12.3). The game universe was topologically a torus T

. Suppose that we modify

the game code so that each bit of the spaceship re-appears at the point diametrically

opposite the point it left. This does not seem like a drastic change until you play a game

with a left-hand drive (US) spaceship. If you send the ship off the screen and watch as it

( b)

(a)

Figure 12.3 A spaceship leaves one side of the screen and returns on the other with (a) torus

boundary conditions, (b) projective-plane boundary conditions. Observe how, in case (b), the

spaceship has changed from being left-handed to being right-handed.

12.2 Integrating p-forms 417

re-appears on the opposite side, you will observe the ship transmogrify into a right-hand-

drive (British) craft. If we ourselves made such an excursion, we would end up starving

to death because all our left-handed digestive enzymes would have been converted to

right-handed ones. The game-space we have constructed is topologically equivalent to

the real projective plane RP

. The lack of a global notion of being left- or right-handed

makes it an example of a non-orientable manifold.

A manifold or surface is orientable if we can choose a global orientation for the

tangent bundle. The simplest way to do this would be to find a smoothly varying set of

basis-vector fields, e

(x), on the surface and define the orientation by choosing an order,

(x), e

(x), ..., e

(x), in which to write them. In general, however, a globally defined

smooth basis will not exist (try to construct one for the two-sphere, S

!). We will, how-

ever, be able to find a continuously varying orientated basis e

(i)

(x), e

(i)

(x), ..., e

(i)

(x)

for each member, labelled by (i), of an atlas of coordinate charts. We should choose

the charts so that the intersection of any pair forms a connected set. Assuming that this

has been done, the orientation of a pair of overlapping charts is said to coincide if the

determinant, det A, of the map e

(i)

= A

(j)

relating the bases in the region of overlap,

is positive.

If bases can be chosen so that all overlap determinants are positive, the

manifold is orientable and the selected bases define the orientation. If bases cannot be

so chosen, the manifold or surface is non-orientable.

Exercise 12.1: Consider a three-dimensional ball B

with diametrically opposite points

of its surface identified. What would happen to an aircraft flying through the surface of

the ball? Would it change handedness, turn inside out or simply turn upside down? Is

this ball an orientable 3-manifold?

12.2 Integrating p-forms

A p-form is naturally integrated over an oriented p-dimensional surface or manifold.

Rather than start with an abstract definition, we will first explain this pictorially, and

then translate the pictures into mathematics.

12.2.1 Counting boxes

To visualize integrating 2-forms let us try to make sense of





dfdg, (12.7)

where  is an oriented two-dimensional surface embedded in three dimensions. The

surfaces f = const. and g = const. break the space up into a series of tubes. The oriented

The determinant will have the same sign in the entire overlap region. If it did not, continuity and con-

nectedness would force it to be zero somewhere, implying that one of the putative bases was not linearly

independent there.

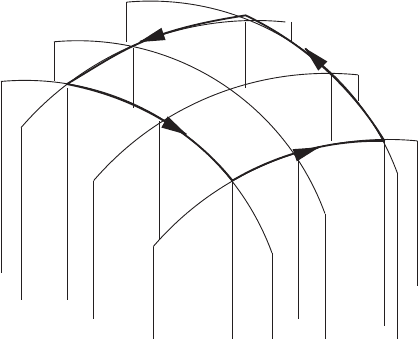
418 12 Integration on manifolds

f=1

f=2

f=3

g=2

g=3

g=4



Figure 12.4 The integration region cuts the tubes into parallelograms.

surface  cuts these tubes in a two-dimensional mesh of (oriented) parallelograms as

shown in Figure 12.4.

We define an integral by counting how many parallelograms (including fractions of a

parallelogram) there are, taking the number to be positive if the parallelogram given by

the mesh is oriented in the same way as the surface, and negative otherwise. To compute





h dfdg (12.8)

we do the same, but weight each parallelogram, by the value of h at that point. The

integral





fdxdy , over a region in R

, thus ends up being the number we would compute

in a multivariate calculus class, but the integral





fdydx would be minus this. Similarly

we compute



df dg dh (12.9)

of the 3-form df dg dh over the oriented volume ", by counting how many boxes defined

by the level surfaces of f , g, h are included in ".

An equivalent way of thinking of the integral of a p-form uses its definition as a

skew-symmetric p-linear function. Accordingly we evaluate





ω, (12.10)

where ω is a 2-form, and  is an oriented 2-surface, by plugging vectors into ω.In

Figure 12.5 we show a tiling of the surface  by a collection of (infinitesimal) parallel-

ograms, each defined by an oriented pair of vector v

and v

that lie in the tangent space

at one corner point x of the parallelogram. At each point x, we insert these vectors into

12.2 Integrating p-forms 419



Figure 12.5 A tiling of  with small oriented parallelograms.

the 2-form (in the order specified by their orientation) to get ω(v

, v

), and then sum the

resulting numbers over all the parallelograms to get I

. Similarly, we integrate a p-form

over an oriented p-dimensional region by decomposing the region into infinitesimal p-

dimensional oriented parallelepipeds, inserting their defining vectors into the form, and

summing their contributions.

12.2.2 Relation to conventional integrals

In the previous section we explained how to think pictorially about the integral. Here,

we interpret the pictures as multivariable calculus.

We begin by motivating our recipe by considering a change of variables in an integral

in R

. Suppose we set x

= x(y

, y

), x

= x

, y

) in





f (x)dx

, (12.11)

and use

∂x

∂y

∂x

∂y

∂x

∂y

∂x

∂y

. (12.12)

Since dy

=−dy

, we have



∂x

∂y

∂x

∂y

−

∂x

∂y

∂x

∂y



. (12.13)

Thus





f (x)dx







f (x(y))

∂(x

, x

)

∂(y

, y

)

(12.14)

420 12 Integration on manifolds

where

∂(x

)

∂(y

)

is the Jacobian determinant

∂(x

, y

)

∂(y

, y

)



∂x

∂y

∂x

∂y

−

∂x

∂y

∂x

∂y



, (12.15)

and 



is the integration region in the new variables. There is therefore no need to include

an explicit Jacobian factor when changing variables in an integral of a p-form over a

p-dimensional space – it comes for free with the form.

This observation leads us to the general prescription: to evaluate





ω, the integral of

a p-form

ω =

...µ

···dx

(12.16)

over the region  of a p-dimensional surface in a d ≥ p dimensional space, substitute a

parametrization

= x

(ξ

, ξ

, ..., ξ

= x

(ξ

, ξ

, ..., ξ

), (12.17)

of the surface into ω. Next, use

∂x

∂ξ

dξ

, (12.18)

so that

ω → ω(x(ξ ))

...i

∂x

∂ξ

···

∂x

∂ξ

dξ

···dξ

, (12.19)

which we regard as a p-form on . (Our customary 1/p! is absent here because we have

chosen a particular order for the dξ’s.) Then





def





ω(x(ξ ))

...i

∂x

∂ξ

···

∂x

∂ξ

dξ

···dξ

, (12.20)

where the right-hand side is an ordinary multiple integral. This recipe is a generalization

of the formula (12.3), which reduced the integral of a 1-form to an ordinary single-

variable integral. Because the appropriate Jacobian factor appears automatically, the

numerical value of the integral does not depend on the choice of parametrization of the

surface.

12.2 Integrating p-forms 421

Example: To integrate the 2-form x dydz over the surface of a two-dimensional sphere

of radius R, we parametrize the surface with polar angles as

x = R sin φ sin θ ,

y = R cos φ sin θ,

z = R cos θ . (12.21)

Then

dy =−R sin φ sin θdφ + R cos φ cos θdθ,

dz =−R sin θ dθ, (12.22)

and so

x dydz = R

sin

φ sin

θ dφdθ . (12.23)

We therefore evaluate



sphere

x dydz = R



2π



sin

φ sin

θ dφdθ

= R



2π

sin

φ dφ



sin

θ dθ

= R



−1

(1 − cos

θ)d cos θ

πR

. (12.24)

The volume form

Although we do not need any notion of length to integrate a differential form, a p-

dimensional surface embedded or immersed in R

does inherit a distance scale from

the R

Euclidean metric, and this can be used to define the area or volume of the

surface. When the cartesian coordinates x

, ..., x

of a point in the surface are given as

(ξ

, ..., ξ

), where the ξ

, ..., ξ

, are coordinates on the surface, then the inherited,

or induced, metric is

“ds

" ≡ g( , ) ≡ g

µν

dξ

⊗ dξ

, (12.25)

where

µν



a=1

∂x

∂ξ

∂x

∂ξ

. (12.26)

422 12 Integration on manifolds

The volume form associated with the induced metric is

d(Volume) =

√

gdξ

···dξ

, (12.27)

where g = det (g

µν

). The integral of this p-form over a p-dimensional region gives the

area, or p-dimensional volume, of the region.

If we change the parametrization of the surface from ξ

to ζ

, neither the dξ

···dξ

nor the

√

g are separately invariant, but the Jacobian arising from the change of

the p-form, dξ

···dξ

→ dζ

···dζ

cancels against the factor coming from the

transformation law of the metric tensor g

µν

→ g



µν

, leading to

√

gdξ

···dξ





dζ

···dζ

. (12.28)

The volume of the surface is therefore independent of the coordinate system used to

evaluate it.

Example: The induced metric on the surface of a unit-radius two-sphere embedded in

is, expressed in polar angles,

“ds

" = g( , ) = dθ ⊗ dθ + sin

θ dφ ⊗ dφ.

Thus

g =

0 sin

= sin

θ,

and

d(Area) = sin θ dθ dφ.

12.3 Stokes’ theorem

All of the integral theorems of classical vector calculus are special cases of

Stokes’ theorem:If∂ denotes the (oriented) boundary of the (oriented) region , then





dω =



∂

ω.

We will not provide a detailed proof. Apart from notation, it would parallel the proof

of Stokes’ or Green’s theorems in ordinary vector calculus: the exterior derivative d has

been defined so that the theorem holds for an infinitesimal square, cube or hypercube. We

therefore divide  into many such small regions. We then observe that the contributions

of the interior boundary faces cancel because all interior faces are shared between two

adjacent regions, and so occur twice with opposite orientations. Only the contribution

of the outer boundary remains.

12.3 Stokes’ theorem 423

Example:If is a region of R

, then from



(xdy− ydx)



= dxdy,

we have

Area () =





dxdy =



∂

(xdy− ydx).

Example: Again, if  is a region of R

, then from d[r

dθ/2]=rdrdθ we have

Area () =





rdrdθ =



∂

dθ .

Example:If is the interior of a sphere of radius R, then





dxdydz =



∂

x dydz =

πR

Here we have referred back to (12.24) to evaluate the surface integral.

Example: Archimedes’ tombstone. Archimedes of Syracuse gave instructions that his

tombstone should have displayed on it a diagram consisting of a sphere and circum-

scribed cylinder. Cicero, while serving as quæstor in Sicily, had the stone restored.

Cicero himself suggested that this act was the only significant contribution by a Roman

to the history of pure mathematics. The carving on the stone was to commemorate

Archimedes’ results about the areas and volumes of spheres, including the one illus-

trated in Figure 12.6, that the area of the spherical cap cut off by slicing through the

cylinder is equal to the area cut off on the cylinder.



1–cos 

Figure 12.6 Sphere and circumscribed cylinder.

Marcus Tullius Cicero, Tusculan Disputations, Book V, Sections 64–66.

424 12 Integration on manifolds

We can understand this result via Stokes’ theorem: if the 2-sphere S

is parametrized

by spherical polar coordinates θ, φ, and  is a region on the sphere, then

Area () =





sin θdθ dφ =



∂

(1 − cos θ)dφ,

and applying this to the figure, where the cap is defined by θ<θ

, gives

Area (cap) = 2π(1 − cos θ

which is indeed the area cut off on the cylinder.

Exercise 12.2: The sphere S

can be thought of as the locus of points in R

n+1

obeying

n+1

i=1

)

= 1. Use its invariance under orthogonal transformations to show that the

element of surface “volume” of the n-sphere can be written as

d(Volume on S

) =



...α

n+1

...dx

n+1

Use Stokes’ theorem to relate the integral of this form over the surface of the sphere

to the volume of the solid unit sphere. Confirm that we get the correct proportionality

between the volume of the solid unit sphere and the volume or area of its surface.

12.4 Applications

We now know how to integrate forms. What sort of forms should we seek to integrate?

For a physicist working with a classical or quantum field, a plentiful supply of interesting

forms is obtained by using the field to pull back geometric objects.

12.4.1 Pull-backs and push-forwards

If we have a map φ from a manifold M to another manifold N , and we choose a point

x ∈ M , we can push forward a vector from TM

to TN

φ(x)

, in the obvious way (map head-

to-head and tail-to-tail). This map is denoted by φ

∗

: TM

→ TN

φ(x)

; see Figure 12.7.

If the vector X has components X

and the map takes the point with coordinates x

to one with coordinates ξ

(x), the vector φ

∗

X has components

(φ

∗

X )

∂ξ

∂x

. (12.29)

This looks like the transformation formula for contravariant vector components under a

change of coordinate system. What we are doing here is conceptually different, however.

A change of coordinates produces a passive transformation – i.e. a new description for

an unchanging vector. A push-forward is an active transformation – we are changing a

vector into a different one. Furthermore, the map from M → N is not being assumed to