Stewart J. College Algebra: Concepts and Contexts
Подождите немного. Документ загружается.

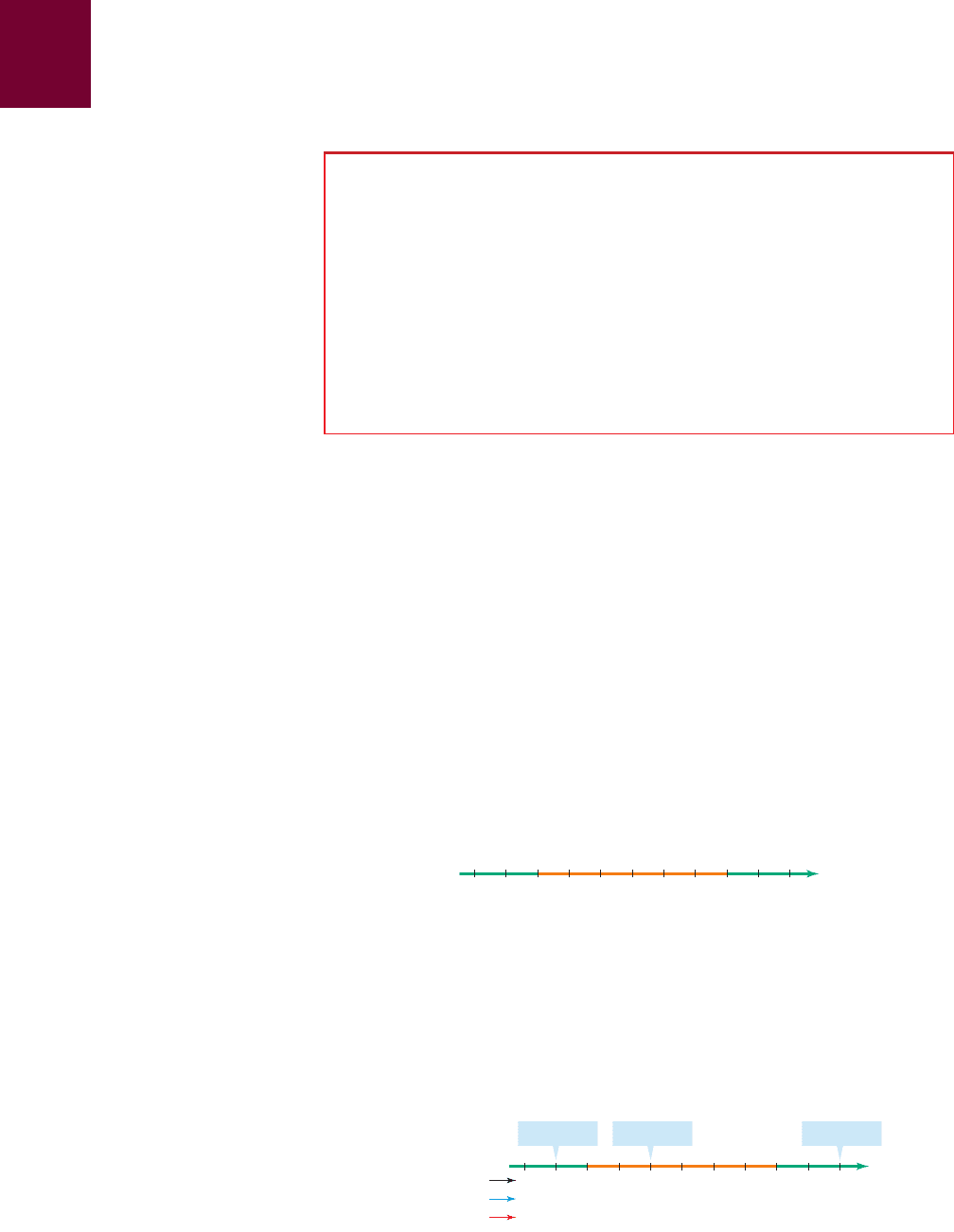
T64 ALGEBRA TOOLKIT C
■
Working with Equations
Solving Nonlinear Inequalities
In the next examples we illustrate the procedure.
1. Move all terms to one side. If necessary, rewrite the inequality so that
all nonzero terms appear on one side of the inequality symbol.
2. Solve the corresponding equation. Solve the equation you get by
replacing the inequality with an equal sign.
3. Find the intervals. The solutions from Step 2 divide the real line into
intervals. Use test values to decide whether the inequality is satisfied on
each interval.
4. Write down the solution. The solution consists of those intervals on
which the inequality is satisfied. Be sure to check the endpoints of each
interval to see whether they also satisfy the inequality.
example
3
Solving a Nonlinear Inequality Algebraically
Solve the inequality .
Solution
First we solve the equation . We do this by factoring the left-hand
side.
Equation
Factor
Solve
These solutions separate the real line into the three intervals , , and
, as shown in the following diagram.14, q 2
1- 2, 421- q, - 22
x = 4
orx = - 2
1x - 421x + 22= 0
x
2
- 2x - 8 = 0
x
2
- 2x - 8 = 0
x
2
- 2x - 8 … 0
0_2 4
The expression is either positive or negative on each of these intervals.
To decide which it is, we pick a test point in the interval and evaluate the expression.
For example, in the interval , let’s pick the test point . Evaluating the
expression at gives us . Since 7 is greater than 0, the ex-
pression is positive on the interval . In the diagram below we
choose test points in each of the three intervals and determine the sign of the ex-
pression on each interval.
1- q, - 22x
2
- 2x - 8
1- 32
2
- 21- 32- 8 = 7- 3
- 31- q, - 22
x
2
- 2x - 8
06_2 4_3x
16_87x™-2x-8
+-+Sign
Test pointTest pointTest point
Now that we know the sign of the expression in each interval, we can label the in-
tervals with “⫹” or “⫺” signs as in the following diagram.
SECTION C.3
■
Solving Inequalities T65
From this diagram we see that the solution of the inequality is the
interval . We have included the endpoints of the interval because the in-
equality requires that the expression be less than or equal to 0.
■ NOW TRY EXERCISE 25 ■
3- 2, 44
x
2
- 2x - 8 … 0
_2 40
______________________++++++++++++++
example
4
Solving a Nonlinear Inequality Algebraically
Solve the inequality .
Solution
First we bring all terms to one side of the inequality. Subtracting gives the
inequality
Next we solve the corresponding equation.
Equation
Factor
Solve
These solutions separate the real line into the three intervals
, as shown in the following diagram.and 13, q 2
1- q, - 12, 1- 1, 32,
x = 3
orx =-1
1x - 321x + 12= 0
x
2
- 2x - 3 = 0
x
2
- 2x - 3 7 0
2x + 3
x
2
7 2x + 3
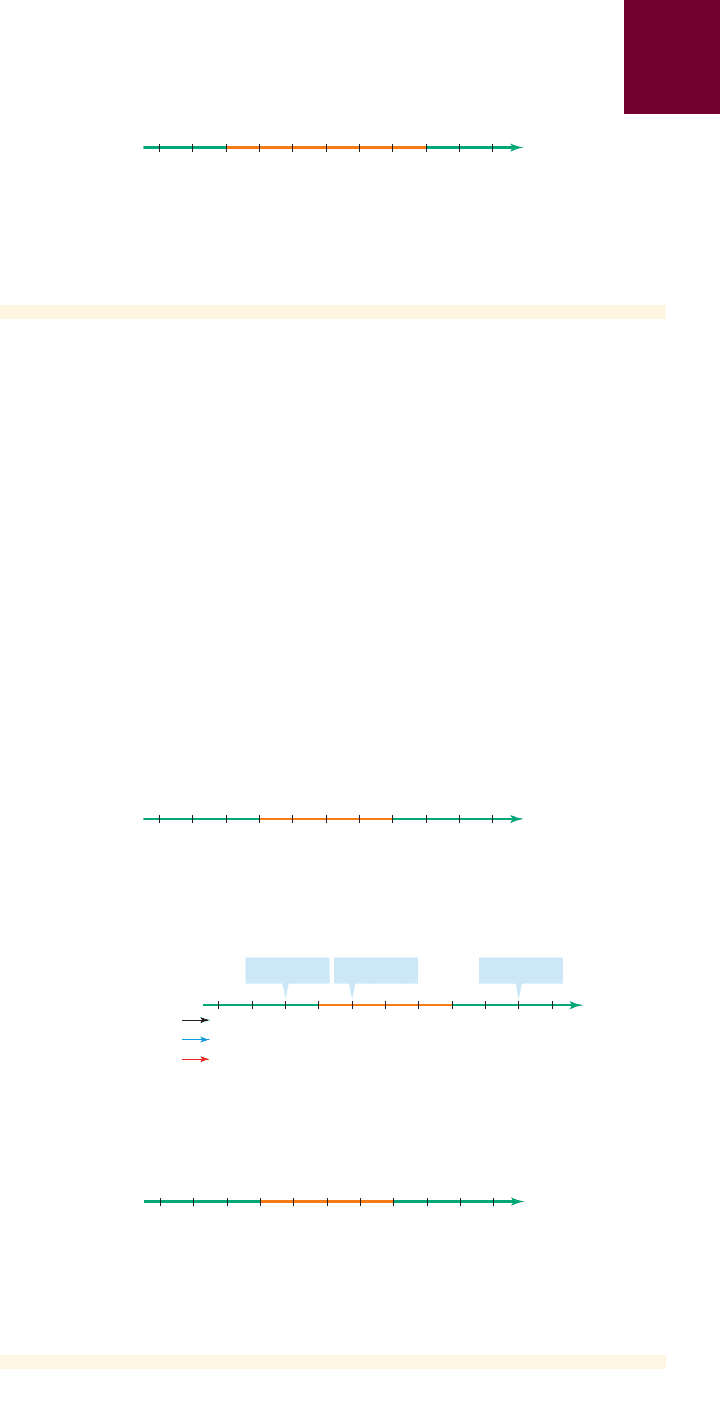
0_1 3
We use test points to determine the sign of the expression on each of
these intervals:
x
2
- 2x - 3
Now that we know the sign of the expression in each interval, we can label the in-
tervals with “+” or “-” signs as in the following diagram.
05_1 3_2x
12_35x™-2x-3
+-+Sign
Test pointTest pointTest point
From the diagram we see that the solution of the inequality con-
sists of all x-values in the set . We did not include the endpoints
and 3 because they do not satisfy the inequality.
■ NOW TRY EXERCISE 27 ■
- 1
1- q, - 12´ 13, q 2
x
2
- 2x - 3 7 0
_1 30
_______________++++++++++++++++++++

T66 ALGEBRA TOOLKIT C
■
Working with Equations
C.3 Exercises
1. Fill in the blank with an appropriate inequality sign.
(a) If , then
___ 2.
(b) If , then 3x
___ 15.
(c) If , then
___ .
(d) If , then
___ 2.
2. True or false?
(a) If , then x and are either both positive or both negative.
(b) If , then x and are each greater than 5.
3–10
■ Let . Determine which elements of S satisfy the
inequality.
3. 4.
5. 6.
7. 8.
9. 10.
11–22
■ Solve the linear inequality. Express the solution using interval notation, and graph
the solution set.
11. 12.
13. 14.
15. 16.
17. 18.
19. 20.
21. 22.
23–34
■ Solve the nonlinear inequality. Express the solution using interval notation, and
graph the solution set.
23. 24.
25. 26.
27. 28.
29. 30.
31. 32.
33. 34. 1x + 3 2
2
1x + 127 01x - 421x + 22
2
6 0
1x - 521x - 2 21x + 1 27 01x + 221x - 1 21x - 3 2… 0
x
2
Ú 9x
2
6 4
x
2
6 x + 22x
2
+ x Ú 1
x
2
+ 5x + 6 7 0x
2
- 3x - 18 … 0
1x - 521x + 4 2Ú 01x + 221x - 3 26 0
1 6 3x + 4 … 16- 1 6 2x - 5 6 7
5 … 3x - 4 … 142 … x + 5 6 4
6 - x Ú 2x + 93x + 11 … 6x + 8
5 - 3x …-167 - x Ú 5
3x + 11 6 52x - 5 7 3
- 4x Ú 102x … 7
x
2
+ 2 6 4
1
x
…
1
2
- 2 … 3 - x 6 21 6 2x - 4 … 7
2x - 1 Ú x3 - 2x …
1
2
x + 1 6 2x - 3 7 0
S = 5- 2, - 1, 0,
1
2
, 1, 12, 2, 46
x + 1x1x + 127 5
x + 1x1x + 127 0
- xx 6-2
- 6- 3xx Ú 2
x … 5
x - 3x 6 5
CONCEPTS
SKILLS
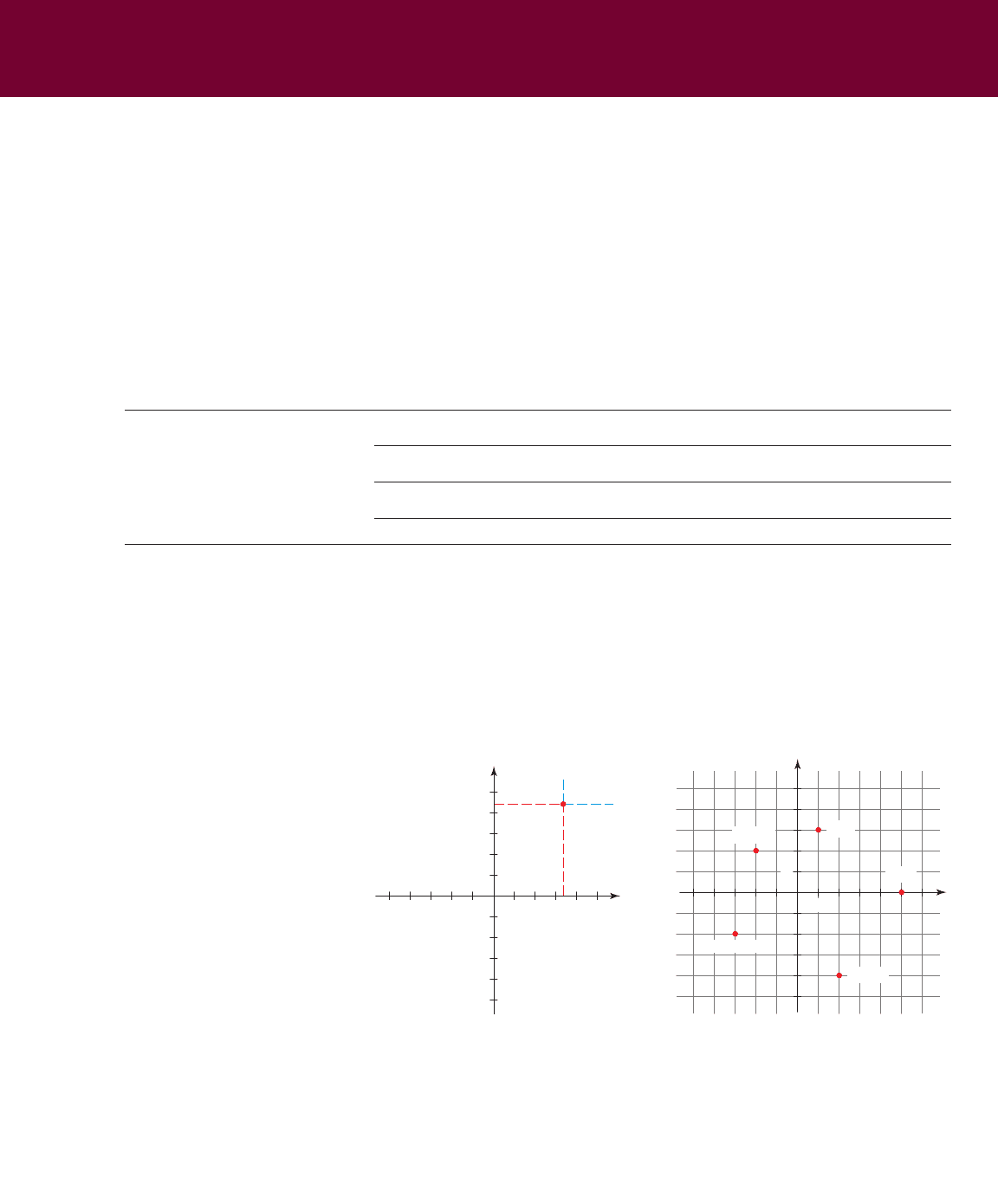
Any point P in the coordinate plane can be located by a unique ordered pair of
numbers (a, b). The first number a is called the x-coordinate of P; the second num-
ber b is called the y-coordinate of P. We can think of the coordinates of P as its “ad-
dress,” because they specify its location in the plane. Several points are labeled with
their coordinates in Figure 2.
T67
Algebra Toolkit D
Working with Graphs
D.1 The Coordinate Plane
D.2 Graphs of Two-Variable Equations
D.3 Using a Graphing Calculator
D.4 Solving Equations and Inequalities Graphically
2
D.1 The Coordinate Plane
■
The Coordinate Plane
■
The Distance Formula
■
The Midpoint Formula
2
■ The Coordinate Plane
Just as points on a line can be identified with real numbers to form the coordinate
line, points in a plane can be identified with ordered pairs of numbers to form the
Cartesian plane or the coordinate plane. To do this, we draw two perpendicular
real lines that intersect at 0 on each line. The horizontal line is the x-axis and the ver-
tical line is the y-axis. The point of intersection of the x-axis and the y-axis is the ori-
gin O. The two axes divide the plane into four quadrants, labeled I, II, III, and IV
in Figure 1. (The points on the coordinate axes are not assigned to any quadrant.)
y
x
P(a, b)
O
b
a
II
III
I
IV
y
x
0
)
)
(_2, 2)
(5, 0)
(1, 3)
(2, _4)
(_3, _2)
1
1
figure 1 figure 2
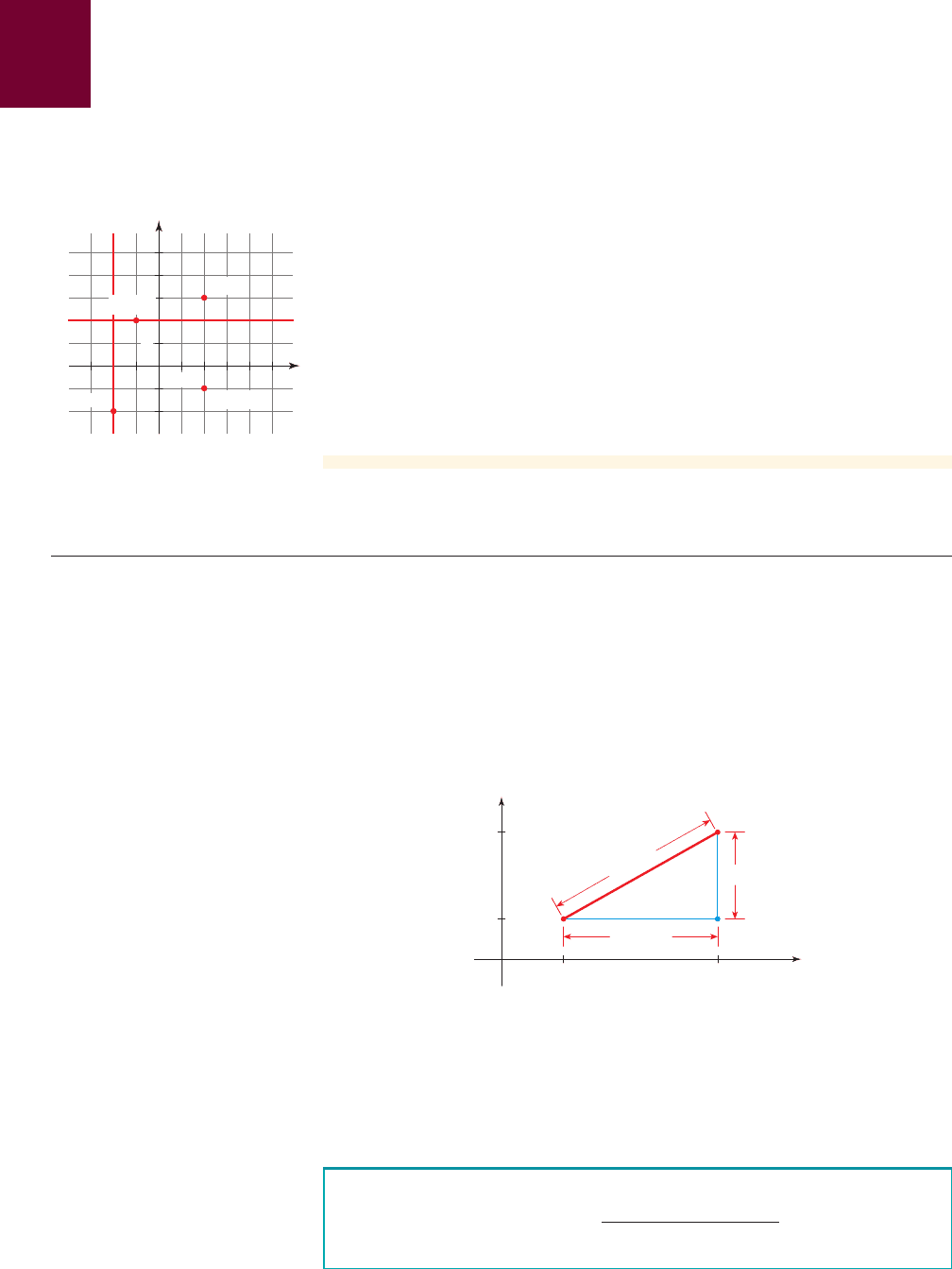
T68 ALGEBRA TOOLKIT D
■
Working with Graphs
example
1
Graphing Points and Sets in the Plane
Graph the set of points in the coordinate plane.
(a)
(b)
(c)
Solution
(a) The points are graphed in Figure 3.
(b) This set consists of all points whose y-coordinate is 2. These points together
form a line parallel to the x-axis (see Figure 3).
(c) This set consists of all points whose x-coordinate is . These points together
form a line parallel to the y-axis (see Figure 3).
■ NOW TRY EXERCISES 5 AND 7 ■
- 2
51x, y20 x =-26
51x, y20 y = 26
512, 32, 1- 1, 22, 12, - 1 2, 1- 2, - 226
y
x
0
)(2, 3)
(2, _1)
(_2, _2)
1
1
(_1, 2)
figure 3 The coordinate plane
2
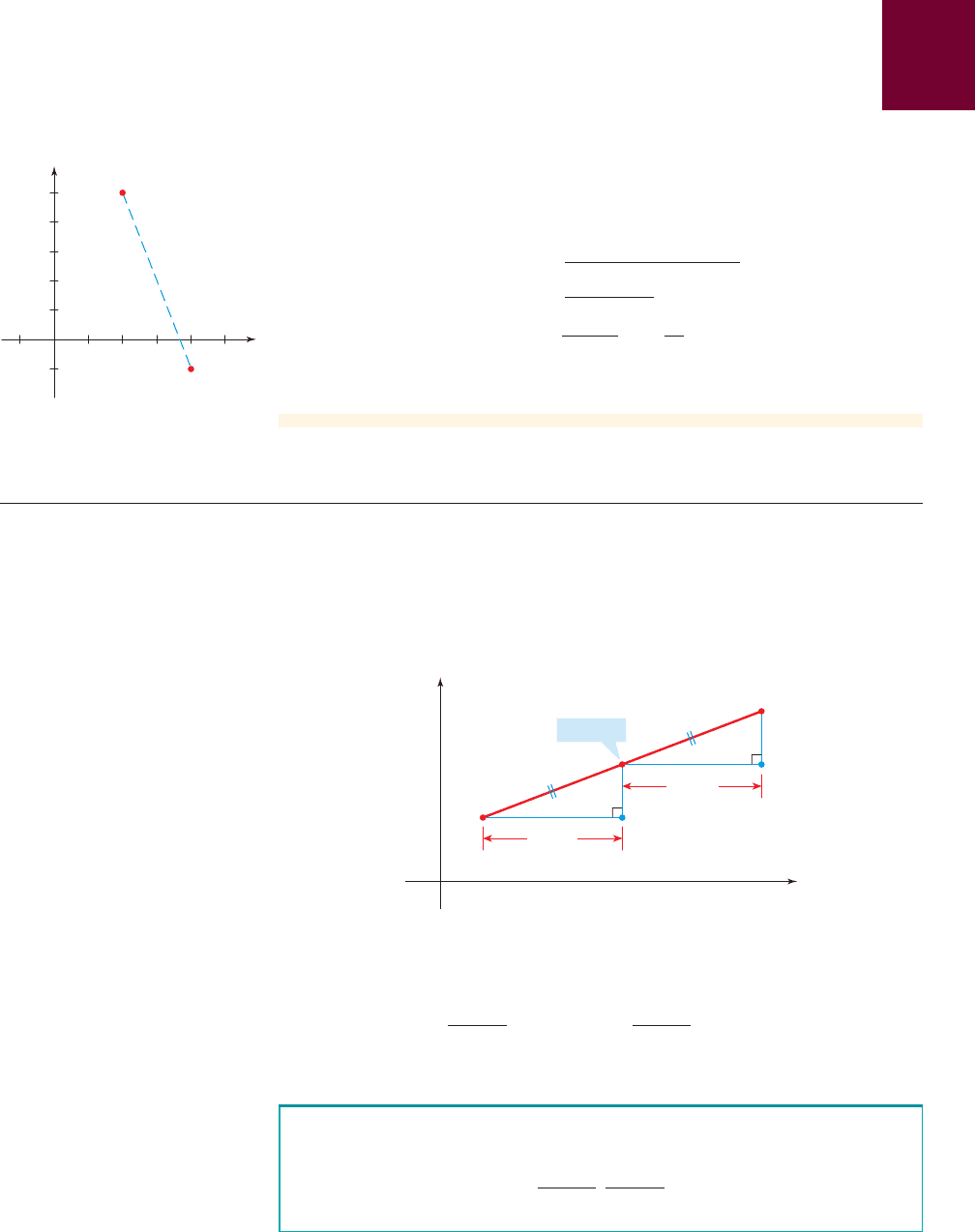
■ The Distance Formula
We now find a formula for the distance d(A, B) between two points and
in the plane. Recall from Algebra Toolkit A.2 that the distance between
points a and b on a number line is . So from Figure 4 we see that
the distance between the points and on a horizontal line must be
and that the distance between and on a vertical line must
be .0
y
2
- y
1
0
C1x
2
, y
1
2B1x
2
, y
2
20 x
2
- x
1
0
C1x
2
, y
1
2A1x
1
, y
1
2
d1a, b 2= 0 b - a 0
B1x
2
, y
2
2
A1x
1
, y
1
2
|
x
2
-x⁄
|
|
y
2
-y⁄
|
A(x⁄, y⁄)
B(x
2
, y
2
)
d (A, B)
C(x
2
, y⁄)
y
x
0
x⁄ x
2
y⁄
y
2
figure 4 Distance between A and B
Since triangle ABC is a right triangle, the Pythagorean Theorem gives the fol-
lowing Distance Formula.
The Distance Formula
The distance between the points and in the plane is
d1A, B 2= 21x
2
- x
1
2
2
+ 1y
2
- y
1
2
2
B1x
2
, y
2
2A1x
1
, y
1
2
SECTION D.1
■
The Coordinate Plane T69
The midpoint of the line segment from to is
a
x
1
+ x
2
2
,
y
1
+ y
2
2
b
B1x
2
, y
2
2A1x
1
, y
1
2
example
2
Finding the Distance Between Two Points
Find the distance between the points and .
Solution
Using the Distance Formula, we have
See Figure 5.
■ NOW TRY EXERCISE 15(b) ■
= 14 + 36 = 140 L 6.32
= 22
2
+ 1- 62
2
d1A, B 2= 214 - 22
2
+ 1- 1 - 52
2
B14, - 12A12, 52
2
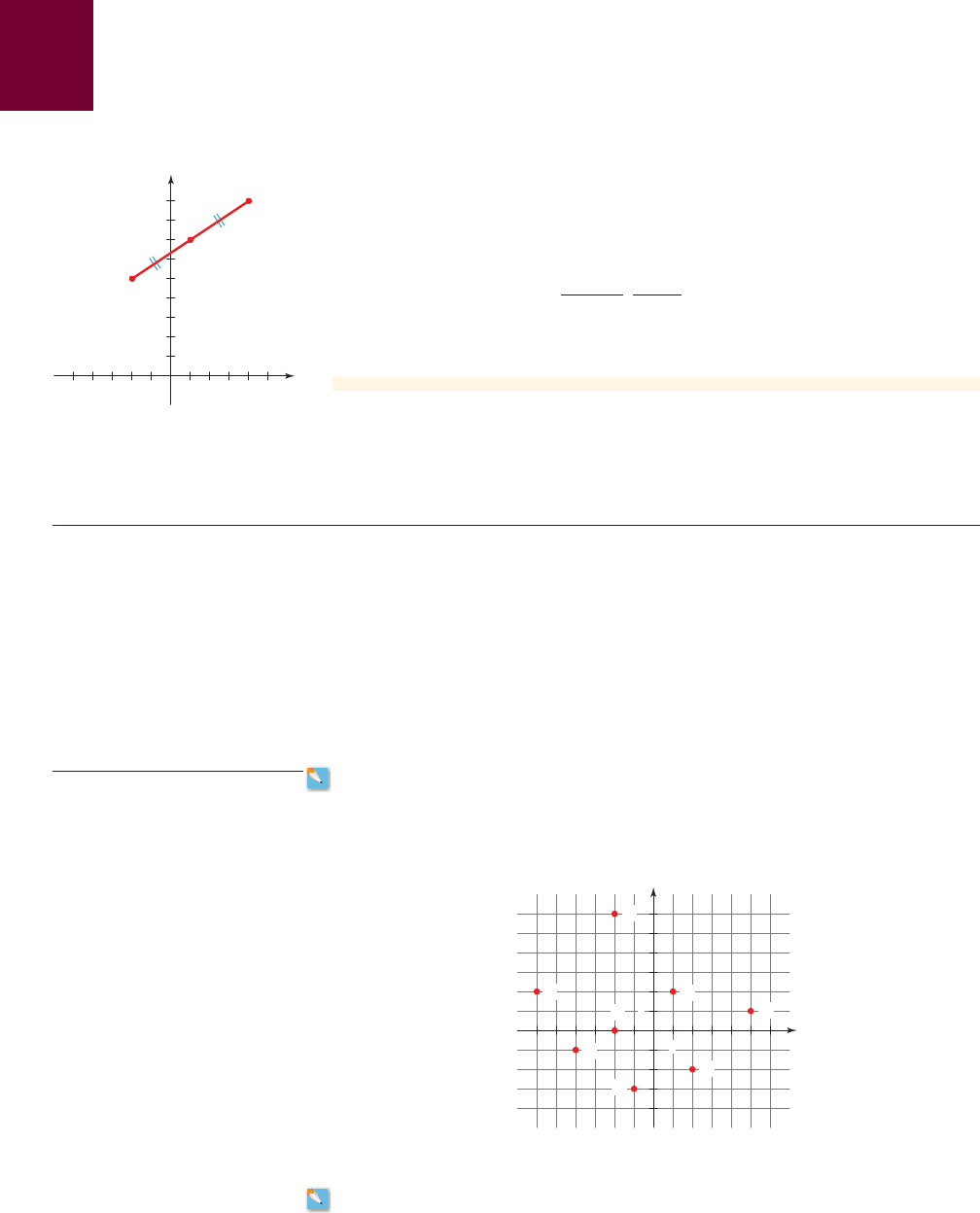
■ The Midpoint Formula
Now let’s find the coordinates (x, y) of the midpoint M of the line segment that joins
the point to the point . In Figure 6, notice that triangles APM and
MQB are congruent because and the corresponding angles are
equal.
d1A, M 2= d1M, B2
B1x
2
, y
2
2A1x
1
, y
1
2
A(2, 5)
B(4, _1)
d(A, B)Å6.32
5
y
x
0
1
1
23 4
2
3
4
5
_
1
figure 5
y
x
0
x-x⁄
x¤-x
A(x⁄, y⁄)
M(x, y)
B(x¤, y¤)
P
Q
Midpoint
figure 6 Midpoint of the line segment AB
It follows that , so . Solving for x, we get
, so . Similarly, .
Midpoint Formula
y =
y
1
+ y
2
2
x =
x
1
+ x
2
2
2x = x
1
+ x
2
x - x
1
= x
2
- xd1A, P2= d1M, Q 2
So the coordinates of the midpoint are the averages of the coordinates of the
endpoints A and B.
T70 ALGEBRA TOOLKIT D
■
Working with Graphs
example
3
Finding the Midpoint
Find the midpoint of the line segment that joins the points and (4, 9).
Solution
Using the Midpoint Formula, we have
So the midpoint of the line segment is the point (1, 7). See Figure 7.
■ NOW TRY EXERCISE 15(c) ■
a
- 2 + 4
2
,
5 + 9
2
b= 11, 7 2
1- 2, 52
y
x
0
_4
4
4
8
(4, 9)
(_2, 5)
(1, 7
)
figure 7
D.1 Exercises
y
x
0
B
A
C
D
E
G
F
H
1
1
CONCEPTS
1. The point that is 3 units to the right of the y-axis and 5 units below the x-axis has the
coordinates (
_______, _______).
2. If x is negative and y is positive, then the point (x, y) is in Quadrant
_______.
3. The distance between the points (a, b) and (c, d ) is
______________. So the distance
between (1, 2) and (7, 10) is
_______.
4. The point midway between (a, b) and (c, d ) is
______________. So the point
midway between (1, 2) and (7, 10) is
_______.
5. Plot the given points in a coordinate plane:
6. Find the coordinates of the points shown in the figure.
12, 3 2, 1- 2, 32, 14, 52, 14, - 52, 1- 4, 52, 1- 4, - 52
SKILLS
7–10 ■ Graph the given set of points in the coordinate plane.
7. 8.
9. 10.
11–14 ■ A pair of points is graphed.
(a) Find the distance between the points.
(b) Find the midpoint of the line segment that joins the points.
51x, y20
x = 5651x, y20 y =-16
51x, y20
y =-2651x, y20 x = 36
SECTION D.2
■
Graphs of Two-Variable Equations T71
11. 12.
0
y
x
1
1
0
y
x
1
1
13. 14.
0
y
x
1
2
0
y
x
1
1
15–24 ■ A pair of points is given.
(a) Plot the points in a coordinate plane.
(b) Find the distance between the points.
(c) Find the midpoint of the line segment that joins the points.
15. (0, 8), (6, 16) 16. , (10, 0)
17. , (4, 18) 18. , (9, 9)
19. 20.
21. (7, 3), (11, 6) 22. (2, 13), (7, 1)
23. (3, 4), 24. (5, 0), (0, 6)1- 3, - 42
1- 1, 62, 1- 1, - 3216, - 22, 1- 1, 32
1- 1, - 121- 3, - 62
1- 2, 52
2
D.2 Graphs of Two-Variable Equations
■
Two-Variable Equations
■
Graphs of Two-Variable Equations
■
Finding Intercepts
■
Equations of Circles
The coordinate plane is the link between algebra and geometry because it allows us
to draw graphs of algebraic equations. The graphs, in turn, allow us to “see” the re-
lationship between the variables in the equation.
2
■ Two-Variable Equations
A two-variable equation is an equation that contains two variables. For example,
the equation
y = 3 + 2x

T72 ALGEBRA TOOLKIT D
■
Working with Graphs
example
1
Reading an Equation
Consider the two-variable equation .
(a) Give a verbal description of the relationship between the variables in the
equation.
(b) Is the ordered pair (2, 4) a solution of the equation? What about (7, 17)?
Solution
(a) The equation says that “subtracting two times y from five times x gives one.”
(b) To check whether (2, 4) is a solution, we replace x by 2 and y by 4 in the equation.
Equation
Replace x by 2 and y by 4
ⴛ False
So (2, 4) is not a solution. You can check that if we replace x by 7 and y by 17, we
get a true equation, so (7, 17) is a solution.
■ NOW TRY EXERCISE 5 ■
2 = 1
5 122- 2142= 1
5 x - 2y = 1
5x - 2y = 1
2
■ Graphs of Two-Variable Equations
We graph an equation by plotting all the solutions of the equation in a coordinate plane.
The Graph of an Equation
example
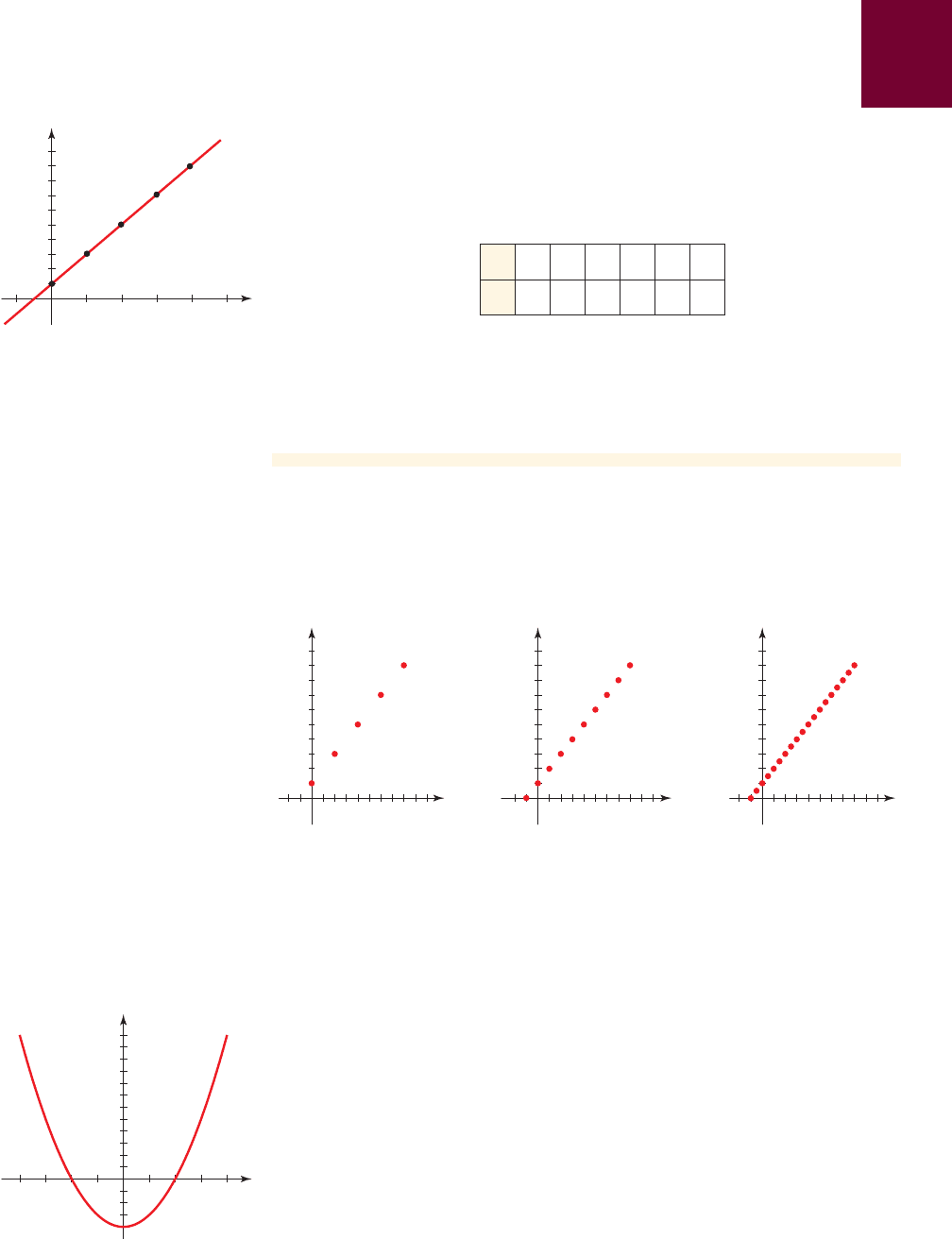
2
Equation, Table, Graph
Consider the equation .
(a) Make a table of the solutions (x, y) of the equation for .
(b) Sketch a graph of the equation.
x = 0, 1, 2, 3, 4, 5
y = 1 + 2x
To check whether (2, 4) is a
solution, replace x by 2 and y by 4.
5x - 2y = 1
is an equation in the two variables x and y. This equation expresses a relationship be-
tween the two variables; we can read the equation as saying
“y is twice x plus 3”
Expressing the equation in words helps us to understand what the equation is telling us.
An ordered pair (a, b) is a solution to an equation, or satisfies an equation, if
the equation is true when x is replaced by a and y is replaced by b. For example,
(1, 5) satisfies the equation because when we replace x by 1 and y by 5,
we get a true equation: .5 = 3 + 2112
y = 3 + 2x
Replace x by 2
and y by 4
The graph of an equation is a curve, so to graph the equation we plot as many points
as we can and then connect them by a smooth curve.
The graph of an equation in x and y is the set of all points (x, y) in the
coordinate plane that satisfy the equation.
SECTION D.2
■
Graphs of Two-Variable Equations T73
(b) We graph the ordered pairs given in the table of part (a). Of course, the
equation has many more solutions than the ones in the table, so we connect
the points by a smooth curve that represents all the solutions of the equation as
in Figure 1.
■ NOW TRY EXERCISE 9 ■
In Example 1 we sketched the graph of the equation by plotting just
a few points. To check that connecting these points by a smooth curve is correct, we
can try graphing more and more points as in Figure 2. The more points we plot, the
more the graph looks like a line.
y = 1 + 2x
y
x
0
1
2
figure 1 Graph of y = 1 + 2x
y
x
0
1
2
y
x
0
1
2
y
x
0
1
2
figure 2 Steps in graphing y = 1 + 2x
x 0 1 2 3 4 5
y 1 3 5 7 9 11
The points on the graph of an equation are solutions of the equation, so we can
read solutions of an equation directly from the graph.
example
3
Reading the Graph of an Equation
The graph of the equation is shown in Figure 3. Answer the following ques-
tions about the solutions of this equation. Then use the equation to confirm your answer.
(a) Is (2, 2) a solution? What about (3, 5)?
(b) What are the value(s) of x when y is 5?
(c) What are the value(s) of y when x is 1?
Solution
We answer these questions from the graph and then from the equation.
(a) From the graph: We see that the point (2, 2) is not on the graph but the point
(3, 5) is on the graph (see Figure 4(a) on the next page). So the ordered pair
(3, 5) is a solution, whereas (2, 2) is not.
y = x
2
- 4
Solution
(a) If x is 0, then , so (0, 1) is a solution. If x is 1, then
, so (1, 3) is a solution. The other entries in the table below
are calculated similarly.
y = 1 + 2112= 3
y = 1 + 2102= 1
1
x
y
2
0
figure 3 Graph of y = x
2
- 4
