Stewart J. College Algebra: Concepts and Contexts
Подождите немного. Документ загружается.


T54 ALGEBRA TOOLKIT C
■
Working with Equations
example
10
Solving for One Variable in Terms of Others
Solve for the variable M in the equation
Solution
Although this equation involves more than one variable, we solve it as usual by iso-
lating M on one side and treating the other variables as we would numbers.
Given equation
Multiply by
Simplify and switch sides
The solution is .
■ NOW TRY EXERCISE 63 ■
M =
r
2
F
Gm
M =
r
2
F
Gm
r
2
Gm
a
r
2
Gm
bF = a
r
2
Gm
ba
Gm
r
2
M b
F = G
mM
r
2
F = G
mM
r
2
C.1 Exercises
CONCEPTS
1. Which of the following equations are linear?
(a) (b) (c)
2. Explain why each of the following equations is not linear.
(a) (b) (c)
3. True or false?
(a) Adding the same number to each side of an equation always gives an equivalent
equation.
(b) Multiplying each side of an equation by the same number always gives an
equivalent equation.
(c) Squaring each side of an equation always gives an equivalent equation.
4. To solve the equation , we take the
_______ root of each side. So the solution
is
_______.
5–8
■ An equation is given.
(a) Express the equation in words.
(b) Determine whether the given value is a solution of the equation.
(c) Solve the equation.
5. 6.
7. 8. 2 - 5x = 8 + x;
- 14x + 7 = 9x - 3;- 2
4x + 9 = 1;
25x - 3 = 12;1
x
3
= 125
3x
2
- 2x - 1 = 01x + 2 = xx1x + 1 2= 6
x + 7 = 5 - 3x
2
x
- 2x = 1
x
2
+ 2x = 10
SKILLS

SECTION C.1
■
Solving Basic Equations T55
9–22 ■ Solve the equation.
9. 10.
11. 12.
13. 14.
15. 16.
17. 18.
19. 20.
21. 22.
23–32
■ Solve the equation.
23. 24.
25. 26.
27. 28.
29. 30.
31. 32.
33–56
■ The given equation involves a power of the variable. Find all real solutions of the
equation.
33. 34.
35. 36.
37. 38.
39. 40.
41. 42.
43. 44.
45. 46.
47. 48.
49. 50.
51. 52.
53. 54.
55. 56.
57–74
■ Solve the equation for the indicated variable.
57. 58.
59. 60. 2lw + 4w = 5l;
for w5xy - 4x = 3y;for x
2t = 5x
3
;for x5x = 7y
2
;for y
41x + 22
5
= 131x - 32
3
= 375
1x + 12
4
+ 16 = 01x + 22
4
- 81 = 0
3x
-6
=
1
5
2x
-4
= 5
5 = 1.8S
7>8
1.3 = 0.5A
3>2
2r
3
+ 10 = 08r
4
- 64 = 0
3x
6
= 456x
4
= 128
z
5
+ 32 = 0A
3
=-27
31x - 52
2
= 151x + 22
2
= 4
6x
2
+ 100 = 0s
2
+ 16 = 0
15r 2
2
- 125 = 014t 2
2
- 64 = 0
y
2
- 7 = 0y
2
- 24 = 0
x
2
= 18x
2
= 49
3
r + 4
=
1
r
+
6r + 12
r
2
+ 4r
z
2z - 4
- 2 =
1
z - 2
2
t
- 5 =
6
t
+ 4
1
x
=
4
3x
+ 1
6
x - 3
=
5
x + 4
2
t + 6
=
3
t - 1
2y - 1
y + 2
=
4
5
2x - 7
2x + 4
=
2
3
5
4w
=
6
7
2
t
=
3
5
2
3
x -
1
4
=
1
6
x -
1
9
2x -
x
2
+
x + 1
4
= 6x
x -
1
3
x -
1
2
x - 5 = 0
2
3
y +
1
2
1y - 32=
y + 1
4
z
5
=
3
10
z + 7
1
2
y - 2 =
1
3
y
r - 231 - 312r + 424= 614Ay -
1
2
B- y = 615 - y2
51x + 32+ 9 =-21x - 22- 1211 - x 2= 311 + 2x2+ 5
5t - 13 = 12 - 5t- 7w = 15 - 2w
4x + 7 = 9x - 13x - 3 = 2x + 6

T56 ALGEBRA TOOLKIT C
■
Working with Equations
61. 62.
63. 64.
65. 66.
67. 68.
69. 70.
71. 72.
73. 74. A
1
2
x
1
B
3
=
5
4x
2
;for x
1
13a
1
2
2
=
1
5a
2
;for a
1
2L
W
= 5;for W
d
t
= s;for t
A = 1.6H
-0.7
;for HA = 0.5S
-1.2
;for S
2.1A = 2.4S
1.8
;for SS = 1.2A
0.4
;for A
F = G
mM
r
2
;for mPV = nRT;for n
V =
4
3
pr
3
;for rP = 2l + 2w;for w
sw = 5 + w;
for wxy = 3y - 2x;for x
2
C.2 Solving Quadratic Equations
■
Solving Quadratic Equations by Factoring
■
Completing the Square
■
Solving Quadratic Equations by Completing the Square
■
The Quadratic Formula
A quadratic equation is an equation of the form
where a, b, and c are real numbers with . We study three methods of solving
quadratic equations: by factoring, by completing the square, or by the Quadratic
Formula.
a ⫽ 0
ax
2
+ bx + c = 0
2
■ Solving Quadratic Equations by Factoring
If a quadratic equation factors easily, then we can use the following property of real
numbers to solve the equation.
Zero-Product Property
AB = 0if and only ifA = 0orB = 0
This means that if we can factor the left-hand side of a quadratic (or other) equation,
then we can solve it by setting each factor equal to 0 in turn. This method works only
when the right-hand side of the equation is 0.
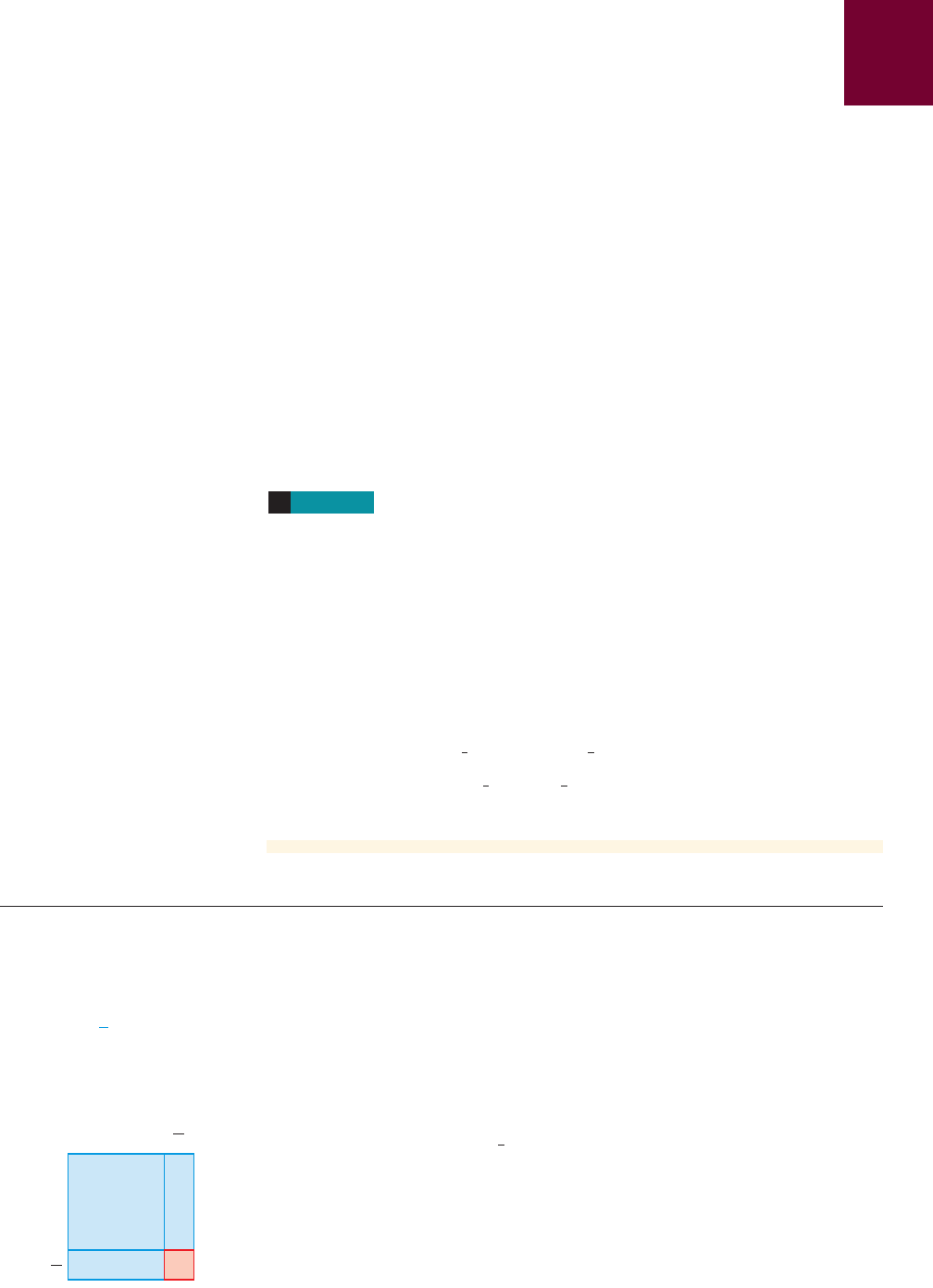
SECTION C.2
■
Solving Quadratic Equations T57
example
1
Solving a Quadratic Equation by Factoring
Solve the quadratic equation.
(a) (b)
Solution
(a) We must first rewrite the equation so that the right-hand side is 0.
Given equation
Subtract 4x and 21
Factor
Zero-Product Property
Solve
The solutions are and
We substitute into the equation: ✓
We substitute into the equation: ✓
(b) The right-hand side is already 0. We can now factor the left-hand side (see
Example 4 in
Algebra Toolkit B.2
):
Given equation
Factor
Zero-Product Property
Solve
The solutions are and . You can check that these are solutions to
the original equations.
■ NOW TRY EXERCISES 5 AND 9 ■
x =
1
2
x =-
5
3
x =-
5
3
x =
1
2
3 x + 5 = 0or2x - 1 = 0
13x + 5212x - 1 2= 0
6 x
2
+ 7x - 5 = 0
7
2
= 4
#
17 2+ 21x = 7
1- 32
2
= 4
#
1- 32+ 21x =-3
✓ CHECK
x = 7.x =-3
x =-3 x = 7
x + 3 = 0orx - 7 = 0
1x + 3 21x - 7 2= 0
x
2
- 4x - 21 = 0
x
2
= 4x + 21
6x
2
+ 7x - 5 = 0x
2
= 4x + 21
2
■ Completing the Square
In
Algebra Toolkit B.2
we learned how to recognize whether an algebraic expression
is a perfect square. In particular, the quadratic expression is a perfect
square (it is the square of ). The constant term of this expression is , and the
coefficient of x is 2a. So the constant term is equal to the square of half of the coef-
ficient of x. This observation allows us to “complete the square” for quadratic ex-
pressions of the form . For example, to make
a perfect square, we must add . Then
is a perfect square. In general we have the following.
x
2
+ 6x + 9 = 1x + 32
2
A
6
2
B
2
= 9
x
2
+ 6x
x
2
+ bx
a
2
x + a
x
2
+ 2ax + a
2
x
x
b
2
b
2
Completing the Square
The area of the blue region is
Add a small square of area to
“complete” the square.
1b>22
2
x
2
+ 2 a
b
2
bx = x
2
+ bx

T58 ALGEBRA TOOLKIT C
■
Working with Equations
Completing the Square
example
2
Completing a Square
Complete the square for the following quadratic expression: .
Solution
The coefficient of is 1, so we can use the completing the square procedure. The
coefficient of x is 3, and half of 3 is . So to complete the square, we add
This gives the perfect square
■ NOW TRY EXERCISE 13 ■
x
2
+ 3x +
9
4
= ax +
3
2
b
2
a
3
2
b
2
=
9
4
3
2
x
2
x
2
+ 3x
2
■ Solving Quadratic Equations by Completing the Square
In
Algebra Toolkit C.1
we learned that an equation of the form can be
solved by taking the square root of each side. This works because the left-hand side
of this equation is a perfect square. So if a quadratic equation does not factor read-
ily, then we can solve it by “completing the square.” The next example illustrates
how this is done.
1x ; a2
2
= c
example
3
Solving Quadratic Equations by Completing the Square
Solve each equation.
(a) (b) 3x
2
- 12x + 6 = 0x
2
- 8x + 13 = 0
To make a perfect square, add , the square of half the coef-
ficient of x. This gives the perfect square
x
2
+ bx + a
b
2
b
2
= ax +
b
2
b
2
a
b
2
b
2
x
2
+ bx
Here are some examples of completing the square.
Expression Add Complete the square
To use the process of completing the square, the coefficient of must be 1.x
2
x
2
- 12x + 36 = 1x - 62
2
A-
12
2
B
2
= 36 x
2
- 12x
x
2
+ 8x + 16 = 1x + 42
2
A
8
2
B
2
= 16 x
2
+ 8x

SECTION C.2
■
Solving Quadratic Equations T59
Solution
(a) When completing the square, we must be careful to add the same constant to
both sides of the equation.
Given equation
Subtract 13
Complete the square: Add
Perfect square
Take square root
Add 4
The solutions are and .
(b) After subtracting 6 from each side of the equation, we must factor the
coefficient of (the 3) from the left-hand side to put the equation in the
correct form for completing the square.
Given equation
Subtract 6
Factor 3 from LHS
Now we complete the square for the expression inside the parentheses,
by adding inside the parentheses. Since everything inside the
parentheses is multiplied by 3, this means that we are actually adding
to the left-hand side of the equation. Thus we must add 12 to the
right-hand side as well.
Complete the square: add 4
Perfect square
Divide by 3
Take square root
Add 2
The solutions are and .
■ NOW TRY EXERCISES 17 AND 21 ■
2 - 122 + 12
x = 2 ; 12
x - 2 = ; 12
1x - 22
2
= 2
3 1x - 22
2
= 6
3 1x
2
- 4x + 42=-6 + 3
#
4
3
#
4 = 12
1- 22
2
= 4
3 1x
2
- 4x2=-6
3 x
2
- 12x =-6
3 x
2
- 12x + 6 = 0
x
2
4 - 134 + 13
x = 4 ; 13
x - 4 = ; 13
1x - 42
2
= 3
a
- 8
2
b
2
= 16 x
2
- 8x + 16 =-13 + 16
x
2
- 8x =-13
x
2
- 8x + 13 = 0
2
■ The Quadratic Formula
If we apply the technique of solving a quadratic equation by completing the square
to the general quadratic equation , we arrive at a formula that
gives us the solutions of the equation in terms of the coefficients a, b, and c. So if
a quadratic equation does not factor readily, we can solve it by using the quadratic
formula.
ax
2
+ bx + c = 0

T60 ALGEBRA TOOLKIT C
■
Working with Equations
example
4
Using the Quadratic Formula
Find all solutions of each equation.
(a)
(b)
(c)
Solution
(a) In this quadratic equation a is 4, b is , and c is . By the Quadratic
Formula,
So the solutions are and .
(b) Using the Quadratic Formula where a is 25, b is , and c is 4 gives
This equation has only one solution, .x =
2
5
x =
- 1- 202; 21- 202
2
- 4
#
25
#
4
2
#
25
=
20 ; 0
50
=
2
5
- 20
13 - 21052>813 + 21052>8
x =
- 1- 32; 21- 32
2
- 414 21- 62
214 2
=
3 ; 2105
8
- 6- 3
x
2
+ 5x + 9 = 0
25x
2
- 20x + 4 = 0
4x
2
- 3x - 6 = 0
The Quadratic Formula
To prove this formula, we complete the square starting with the general quad-
ratic equation. First, we move the constant term to the right-hand side and then di-
vide each side of the equation by a.
Quadratic equation
Subtract c
Divide by a
Complete the square: Add
Perfect square; common denominator
Take square roots
Subtract
This completes the proof.
b
2a
x =
- b ; 2b
2
- 4ac
2a
x +
b
2a
= ;
2b
2
- 4ac
2a
ax +
b
2a
b
2
=
- 4ac + b
2
4a
2
a
b
2a
b
2
x
2
+
b
a
x + a
b
2a
b
2
=-
c
a
+ a
b
2a
b
2
x
2
+
b
a
x =-
c
a
ax
2
+ bx =-c
ax
2
+ bx + c = 0
The solutions of the quadratic equation , where , are
x =
- b ; 2b
2
- 4ac
2a
a ⫽ 0ax
2
+ bx + c = 0
4x
2
- 3x - 6 = 0
a = 4
c =-6
b =-3

SECTION C.2
■
Solving Quadratic Equations T61
(c) Using the Quadratic Formula where a is 1, b is 5, and c is 9 gives
Since the square of any real number is nonnegative, is undefined in the
real number system. The equation has no real solution.
■ NOW TRY EXERCISES 29, 33, AND 35 ■
2- 11
x =
- 5 ; 25
2
- 4
#
1
#
9
2
=
- 5 ; 2- 11
2
C.2 Exercises
CONCEPTS
1. The Quadratic Formula gives us the solutions of the equation .
(a) State the Quadratic Formula:
_______.
(b) In the equation the coefficient a is
_______, b is _______, and
c is
_______. So the solution of the equation is _______.
2. Explain how you would use each method to solve the equation .
(a) By factoring:
_______
(b) By completing the square: _______
(c) By using the Quadratic Formula: _______
3–10 ■ Solve the equation by factoring.
3. 4.
5. 6.
7. 8.
9. 10.
11–14
■ Complete the square for the given expression.
11. 12.
13. 14.
15–22 ■ Solve the equation by completing the square.
15. 16.
17. 18.
19. 20.
21. 22.
23–36
■ Solve the equation by factoring or using the Quadratic Formula.
23. 24.
25. 26.
27. 28.
29. 30.
31. 32.
33. 34.
35. 36. 5x
2
- 7x + 5 = 03x
2
+ 2x + 2 = 0
3 + 5z + z
2
= 0w
2
= 31w - 12
2y
2
- y -
1
2
= 0z
2
-
3
2
z +
9
16
= 0
x
2
- 6x + 1 = 03x
2
+ 6x - 5 = 0
2x
2
- 8x + 4 = 0x
2
+ 3x + 1 = 0
x
2
+ 30x + 200 = 0x
2
- 7x + 10 = 0
x
2
+ 5x - 6 = 0x
2
- 2x - 15 = 0
5x
2
+ 15x + 1 = 04x
2
- 20x - 2 = 0
3x
2
- 6x - 1 = 02x
2
+ 8x + 1 = 0
x
2
+ 3x -
7
4
= 0x
2
- 6x - 11 = 0
x
2
- 4x + 2 = 0x
2
+ 2x - 5 = 0
x
2
-
2
3
x +
ⵧ
= 1x +
ⵧ
2
2
x
2
-
1
2
x +
ⵧ
= 1x +
ⵧ
2
2
x
2
+ x +
ⵧ
= 1x +
ⵧ
2
2
x
2
+ 7x +
ⵧ
= 1x +
ⵧ
2
2
4w
2
= 4w + 32y
2
+ 7y + 3 = 0
4x
2
- 4x - 15 = 03x
2
- 5x - 2 = 0
x
2
+ 8x + 12 = 0x
2
- 7x + 12 = 0
x
2
+ 3x = 4x
2
+ x = 12
x
2
- 4x - 5 = 0
x =
1
2
x
2
- x - 4 = 0
x =
ax
2
+ bx + c = 0
SKILLS
T62 ALGEBRA TOOLKIT C
■
Working with Equations
2
■ Solving Inequalities
An inequality looks just like an equation, except in place of the equal sign we have
one of the symbols Here is an example of an inequality:
The table in the margin shows that some numbers satisfy the inequality and some
numbers don’t.
To solve an inequality in one variable means to find all values of the variable
that make the inequality true. Unlike an equation, an inequality generally has infi-
nitely many solutions, which form an interval or a union of intervals on the real line.
The following illustration shows how an inequality differs from its corresponding
equation.
Solution Graph
Equation:
Inequality:
The idea in solving an inequality is to “do the same thing to each side of the in-
equality.” We use the following rules when working with inequalities.
Operations on Inequalities
x … 34x + 7 … 19
x = 34x + 7 = 19
4x + 7 … 19
6, 7, …, or Ú.
2
C.3 Solving Inequalities
■
Solving Inequalities
■
Solving Linear Inequalities
■
Solving Nonlinear Inequalities
In this section we review inequalities and how to solve them algebraically. In
Algebra Toolkit D.4
we solve inequalities graphically. We will see that the graphi-
cal method helps us understand why the algebraic method works. We begin by re-
viewing the basic properties of inequalities.
x
4x ⴙ 7 … 19
1
✓
11 … 19
2
✓
15 … 19
3
✓
19 … 19
4
23 … 19
5
27 … 19
0 3
0 3
Pay special attention to Rules 2 and 3. Rule 2 says that we can multiply (or di-
vide) each side of an inequality by a positive number, but Rule 3 says that if we mul-
tiply each side of an inequality by a negative number, then we reverse the direction
of the inequality. For example, if we start with the inequality and multiply by
5, we get , but if we multiply by , we get .- 5 7-10- 55 6 10
1 6 2
1. Add (or subtract) the same quantity to each side.
2. Multiply (or divide) each side by the same positive quantity.
3. Multiply (or divide) each side by a negative quantity and reverse the
direction of the inequality.
ⴛ
ⴛ

SECTION C.3
■
Solving Inequalities T63
2
■ Solving Linear Inequalities
An inequality is called a linear inequality if the corresponding equation (the equa-
tion obtained by replacing the inequality sign with an equal sign) is linear. To solve
a linear inequality, we use operations on inequalities to isolate the variable on one
side of the inequality.
example
1
Solving a Linear Inequality
Solve the inequality and graph the solution set.
Solution
We use the operations on inequalities to isolate the variable x on one side of the in-
equality.
Inequality
Subtract 9x from each side
Simplify
Multiply by , reverse inequality
Simplify
The solution set consists of all numbers greater than . In other words, the solution
of the inequality is the interval . It is graphed in Figure 1.
■ NOW TRY EXERCISE 17 ■
A-
2
3
, qB
-
2
3
x 7-
2
3
-
1
6
A-
1
6
B1- 6x27 A-
1
6
B4
- 6x 6 4
3 x - 9x 6 9x + 4 - 9x
3 x 6 9x + 4
3x 6 9x + 4
0
_
2
3
figure 1 The interval A-
2
3
, qB
example
2
Solving a Pair of Linear Inequalities
Solve the inequalities , and graph the solution set.
Solution
We use the operations on inequalities to isolate the variable x.
Inequality
Add 2 to each side
Divide each side by 3
Therefore, the solution set is the interval , as shown in Figure 2.
■ NOW TRY EXERCISE 21 ■
32, 52
2 … x 6 5
6 … 3x 6 15
4 … 3x - 2 6 13
4 … 3x - 2 6 13
0
25
figure 2 The interval 32, 52
2
■ Solving Nonlinear Inequalities
If an inequality involves squares or higher powers of the variable, it is nonlinear. The
key idea in solving a nonlinear inequality algebraically is to first find the solutions
of the corresponding equation, then use test values to determine whether the given
inequality is satisfied on the intervals determined by these solutions. This method is
described as follows.
