Станішевський С.О. Вища математика. Конспект лекцій. Модуль 1
Подождите немного. Документ загружается.

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
80
ЛЕКЦІЯ № 16
Системи лінійних алгебраїчних рівнянь та методи їх розв'я-
зання. Система т лінійних алгебраїчних рівнянь з n невідомими x
1
, x
2
,
..., x
n
має вигляд:
11 1 12 2 1n n 1
21 1 22 2 2n n 2
m1 1 m2 2 mn n m
а х а х
...
а х
b ,
а х а х
...
а х
b ,
... ... ... ... ...
... ... ... ,
а х а х
...
а х
b .
⋅ + ⋅ + + ⋅ =
⋅ + ⋅ + + ⋅ =
⋅ + ⋅ + + ⋅ =
(3.4)
Величини а
11
, а
12
,…, а
1n
, a
21
, a
22
, … , a
mn
звуть коефіцієнтами;
1
х
,
2
х
,…,
n
x
– невідомими. Індекси біля коефіцієнтів означають номер
рівняння та номер невідомого. Величини b
1
, b
2
, …, b
m
– звуть вільними
членами.
Система рівнянь однорідна, якщо всі b
i
= 0(
m,1
і
=
), і неоднорі-
дна, якщо хоча б одне b
i
0
≠
.
Упорядковану множину n чисел k
1
, k
2
. ..., k
n
звуть розв’язком си-
стеми (3.4), якщо при їх підстановці у (3.4) замість невідомих х
1
, х
2
, ....
х
n
усі рівняння системи (3.4) перетворюються у тотожності. Система
рівнянь сумісна, якщо вона має хоча б один розв'язок, і несумісна, як-
що вона не має жодного розв'язку.
Сумісну систему лінійних рівнянь звуть визначеною, якщо вона
має єдиний розв'язок.
Сумісна система лінійних рівнянь є невизначеною, якщо розв'я-
зків більше ніж один.
Система однорідних рівнянь завжди має нульовий розв'язок:
х
1
= х
2
= ...= х
n
= 0.
Якщо система однорідних рівнянь має ненульовий розв'язок k
1
,
k
2
..., k
n
, (тобто, хоча б одне з цих чисел відмінне від нуля), то така сис-
тема має і незліченну множину розв'язків вигляду
α
k
1
,
α
k
2,
...,
α
k
n
, де
R
∈
α
.
Методи розв’язання. Метод послідовного виключення невідо-
мих (метод Гаусса). Цей метод вивчається у середній школі.
Приклад. Розв'язати систему:

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
81
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
3
х 3х 9х 5х 2,
2
х 3х 11х 5х 2,
х х 5х 2х 1,
2
х х 3х 4х 3,
х х 3х 4х 3.
+ + + = −
+ + + =
+ + + =
+ + + = −
+ + + = −
Розв'язання. Третє рівняння перепишемо першим і виключимо
невідоме х
1
із решти рівнянь. З третього рівняння виключимо х
2
і пере-
пишемо систему.
1 2 3 4 1 2 3 4
3 4 2 3 4
2 3 4 3 4
2 3 4
3 4
х х 5х 2х 1, х х 5х 2х 1,
6х х 5, х 7х 2 х 5,
х х х 0, 6х х 5,
х 7х 2х 5, 6х
2х 2х 4.
+ + + = + + + =
+ = + + =
+ + = + =
+ + =
− =
1 2 3 4
2 3 4
3 4
3 4
4
3 4
х х 5х 2х 1,
х 7х 2 х 5,
6
х х 5,
х 5,
-2
х 2.
х х 2.
+ + + =
+ + =
+ =
+ =
=
− =
Маємо два однакових рівняння (третє та четверте). Виключимо
невідоме х
3
із останнього рівняння.
Отримані системи еквівалентні даній системі і з неї послідовно
знизу вгору знаходимо: х
4
= –1; х
3
= 1; х
2
= 0; х
1
= –2. Тобто, система
сумісна і визначена.
Формули Крамера. Розглянемо систему (3.4), коли m = n. Такі
системи звуться крамерівськими. Запишемо визначники:
nn n21n
n22221
n121 11
n
а ...а а
.. ... ... ...
а ... а а
а ... аа
=
∆
,
nn n2n
n2222
n112 1
х
а ...а b
.. ... ... ...
а ... а b
а ... аb
1
=
∆
,
nn n1n
n2221
n11 11
х
а ...b а
.. ... ... ...
а ... b а
а ... b а
2
=
∆
, . . . ,
n n21n
22221
112 11
х
b ...а а
.. ... ... ...
b ... а а
b ... а а
n
=
∆
.
Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
82
∆
n
- головний визначник системи;
n21
ххх
,.... , ,
∆∆∆
- допоміжні
визначники, які утворені заміною і-гo стовпця у головному визначнику
стовпцем вільних членів системи (3.4). Якщо
0
n
≠
∆
, то за формулами
Крамера:
nхі
/х
і
∆∆
=
, тут
n
0
∆
≠
. (3.5)
Випадок, коли
0
n
=
∆
розглянемо нижче.
Приклад. Розв'язати систему:
1 2 3
1 2 3
2 3
2
х х 3х 3,
3
х 4х 5х 8,
2
х 7х 17.
− − =
+ − = −
+ =
Обчислимо визначники:
3
2 1 3
3 4 5 79
0 2 7
∆
− −
= − =
;
1
х
3 1 3
8 4 5 395;
17 2 7
∆
− −
= − − =
2
х
2 3 3
3 8 5 158;
0 17 7
∆
−
= − − = −
3
х
2 1 3
3 4 8 237;
0 2 17
∆
−
= − =
За формулами (3.5):
1
х 395 / 79 5
= =
;
2
х 158 /79 2
= − = −
;
3
х 237 / 79 3
= =
. Відповідь: x
1
= 5; х
2
= –2; х
3
= 3.
Матричний метод. Для запису системи т лінійних рівнянь з п
невідомими використовується і більш коротка (матрична) форма запи-
су. Записавши коефіцієнти при невідомих у вигляді матриці А, невідо-
мі і вільні члени у вигляді матриць Χ і В, систему (3.4) можна записати
у вигляді:
В
Х
А
=
⋅
. Тобто:
11 21 1n
1 1
21 22 2n 2 2
n n
m1 m2 mn
а а ... а
х b
а а ... а х b
... ...
... ... ... ..
х b
а а ... а
=
. (3.6)
Побудуємо нову матрицю приєднанням матриці В до А. Цю ма-
трицю позначимо
А
. Вона має назву розширеної матриці.

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
83
=
3
2
1
nm2m1m
n22221
n11211
b
...
b
b
а...аа
............
а...аа
а...аа
А
.
Повну відповідь на питання про існування розв'язку системи т
лінійних рівнянь з n невідомими дає теорема Кронекера-Капеллі, яку
приймемо без доведення.
Теорема. Щоб система рівнянь (3.6) мала розв'язок, необхідно і
достатньо, щоб ранг розширеної матриці дорівнював рангу основної
матриці.
Якщо ранги основної і розширеної матриць збігаються з числом
невідомих, то система має єдиний розв'язок.
Якщо ранг основної і розширеної матриць менший від числа не-
відомих, то система має більш ніж один розв'язок, тобто несчислену
множину.
В останньому випадку число "вільних" невідомих, через які ви-
ражається решта невідомих, які мають назву "базові" невідомі, дорів-
нює n – r. Припустимо, що rang (А) = rang(
А
) = n і т = n. Тоді матри-
ця А є невиродженою і для неї є обернена матриця А
–1
. Розв'яжемо ма-
тричне рівняння таким чином:
.ВАХАА
11
⋅=⋅⋅
−−
Оскільки
Е
А
А
1
=
⋅
−
, тоді
В
А
Х
1
⋅
=
−
. Тобто для рішення сис-
теми п лінійних рівнянь з п невідомими, коли матриця А невироджена,
достатньо знайти обернену матрицю А
–1
і знайти добуток двох матриць
А
–1
і В, це буде матриця стовпець. Відповідні елементи матриці стовп-
ця Χ будуть дорівнювати елементам матриці стовпця добутку. Це і
буде розв'язком системи.
Приклад. Розв'язати систему рівнянь матричним методом:
=+−
−=+−
=+−
.1z y х
,1z3y5х
,3z y4 х2
Розв’язання.
2 4 1
А 1 5 3
1 1 1
−
= −
−
,
=
=
1
1-
3
В,
z
у
х
Х
.
3
2 4 1
1 5 3 8
1 1 1
∆
−
= − = −
−
,
Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
84
отже А - невироджена і її
(
)
rang
А 3
=
.
Запишемо розширену матрицю системи і визначимо її ранг.
( )
2 4 1 3 0 1 0 0
А 1 5 3 1 0 0 1 1 , rang А 3.
1 1 1 1 1 0 0 2
−
= − − ≈ − =
Оскільки
(
)
rang
А
=
(
)
rang
А 3
=
, то за теоремою Кронекера-
Капеллі система сумісна і має єдиний розв’язок. Ранг розширеної мат-
риці шукали за методом елементарних перетворень матриці. Оскільки
оперували тільки з її строками, то одержали розв’язок даної системи.
Для цього останню трансформовану матрицю
А
запишемо у вигляді:
1 0 0 2 x
0 1 0 0 y
0 0 1 1 z
=
−
.
Тобто х = 2, y = 0, z = –1 є розв'язок даної системи.
Приклад. Розв'язати систему однорідних рівнянь:
1 2 3
1 2 3
1 2 3
3
х х 2х 0,
2
х 4х 5х 0,
х 2х 3х 0.
− + =
− + =
+ + =
Розв’язання.
.1130688536
321
542
213
3
=−−++−=
−
−
−
=
∆
Оскільки
0
3
≠
∆
,
( )
(
)
rang A rang A 3
= =
, то за теоремою Кро-
некера-Капеллі система має єдиний тривіальний розв'язок:
.0ххх
321
===
Приклад. Розв'язати систему однорідних рівнянь:
1 2 3
1 2 3
1 2 3
3
х 4х х 0,
х 3х 5х 0,
4
х х 4х 0.
+ − =
− + =
+ + =
Розв’язання
:

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
85
.015161218036
414
531
143
3
=−−−−+−=−
−
=
∆
Оскільки
0
3
=
∆
- система сумісна, але невизначена. Ранг цієї
системи дорівнює двом. Одне з рівнянь можна виключити.
1 2 3
1 2 3
3
х 4х х 0,
х 3х 5х 0.
+ − =
− + =
Виразимо х
1
і х
2
через х
3
:
−=−
=+
,х5х3х
,х х4х3
321
321
Розв'яжемо останню систему за формулами Крамера або за ме-
тодом виключення невідомих. Виконайте самостійно.
Отримаємо: х
1
= (-17/13)х
3
; х
2
= (16/13)х
3
. Нехай х
3
= 13k, де
Rk
∈
, тоді розв'язок початкової системи:
.k13х ,k16х ,k17х
321
==−=
ТЕМА 4. ЕЛЕМЕНТИ ВЕКТОРНОЇ АЛГЕБРИ
ЛЕКЦІЯ № 17
Вектори. Основні поняття. Нехай А і В - дві різні точки пло-
щини або простору. Відрізок AВ, в якому точку А вважають початком,
а точку В - кінцем, називають вектором АВ і позначають
АВ
. Тобто
вектор - це напрямлений відрізок. Напрям, який визначається проме-
нем АВ, називають напрямом вектора
АВ
, а довжину відрізка |АВ|
називають довжиною (або модулем) вектора
АВ
. Довжину (модуль)
вектора
АВ
позначають |
АВ
|. На рисунках вектор
АВ
звичайно зо-
бражують прямолінійною стрілкою з початком у точці А і кінцем у
точці В.
Серед усіх векторів з початком у точці А є один вектор, довжина
якого дорівнює нулю. Його називають нульовим вектором і познача-
ють
АА
. Поняття напряму для нульового вектора не вводять.
Рівність векторів. Нехай
АВ
і
СD
- два вектори. Вектор
АВ
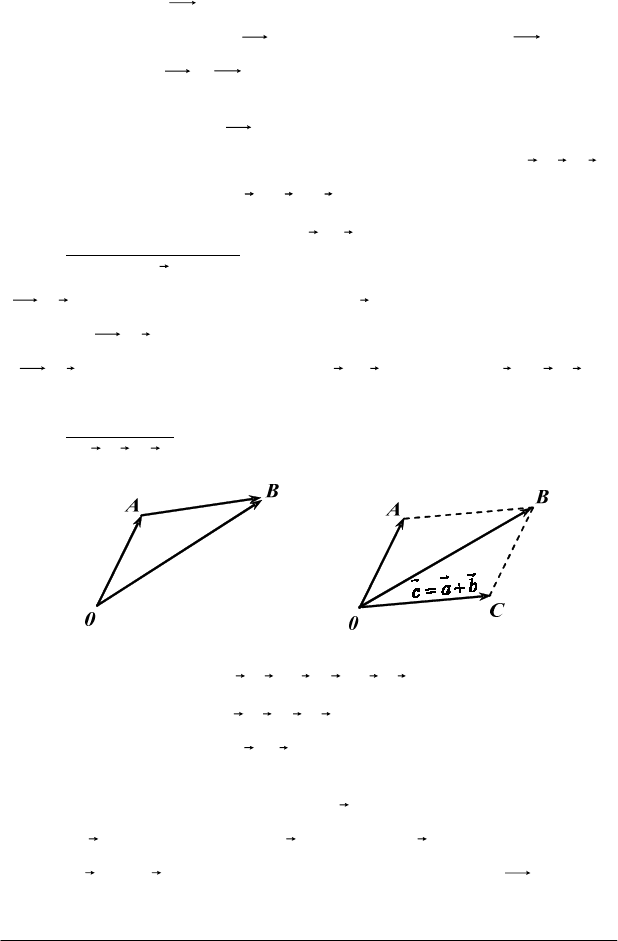
Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
86
дорівнює вектору
СD
, якщо:
1) довжина відрізка
АВ
дорівнює довжині відрізка
СD
;
2) промені
АВ
і
СD
однаково напрямлені.
За такого означення рівності векторів множину всіх векторів,
які дорівнюють вектору
АВ
, називають вільним вектором. Вільні век-
тори звичайно позначають малими латинськими буквами:
а
,
b
,
с
, а
їхні довжини - відповідно
|а|
,
|b|
,
|с|
.
Додавання векторів. Нехай
а
і
b
- два не нульові вектори. Від-
кладемо вектор
а
від точки О і позначимо його кінець буквою А:
аОА =
. Відкладемо від точки А вектор
b
і позначимо його кінець бу-
квою В:
bАВ =
. Вектор з початком у точці О і кінцем у точці В
(
сОВ =
) називають сумою векторів
а
і
b
і записують
с
=
а
+
b
. Це
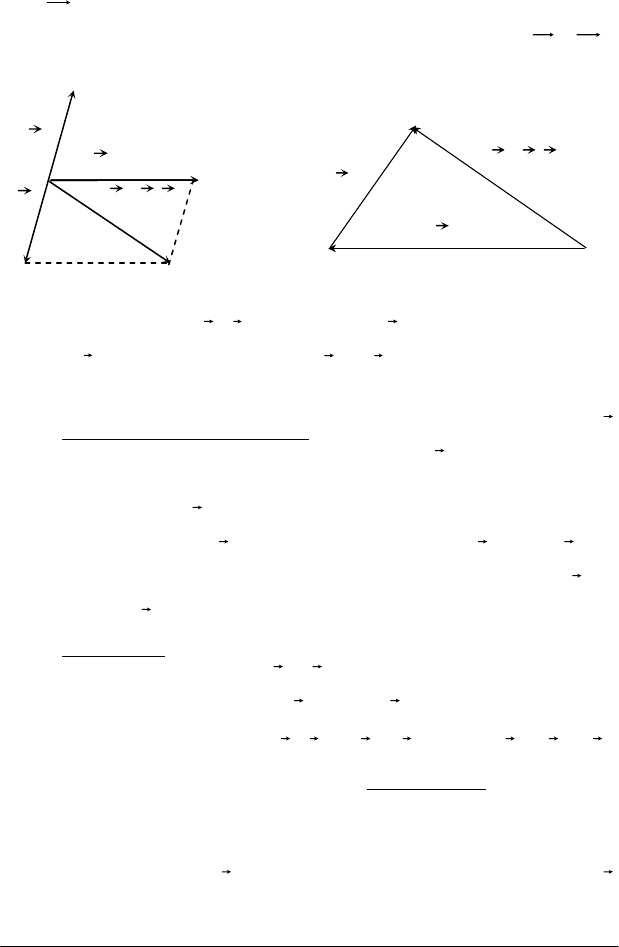
правило трикутника (рис.4.1).
Властивості операції додавання векторів:
1)
аоа =+
;
а
r
а
r
b
r
b
r
с а b
= +
r r r
Рис. 4.1 Рис. 4.2
2) асоціативність:
)сb(ас)bа( ++=++
;
3) комутативність:
аbbа +=+
.
Суму двох векторів
а
і
b
можна побудувати за правилом пара-
лелограма (рис. 4.2).
Вектор, протилежний вектору
а
, це такий вектор (його позна-
чають
а−
), що сума вектора
а
і вектора
а−
дорівнює нульовому
вектору:
а
+ (
а−
) =
0
r
. Вектор, протилежний вектору
АВ
, познача-
Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
87
ють
ВА
.
Ненульові протилежні вектори мають рівні довжини (
|a||а| −=
)
і протилежні напрями.
Рис. 4.3 Рис. 4.4
Різниця двох векторів
bа −
є сума вектора
а
і вектора, протилежного
вектору
b
(рис. 4.3), тобто вектор
)b(а −+
. Або її можна знайти за
правилом трикутника (рис.4.4).
Множення вектора на число. Добутком ненульового вектора
а
на число λ називають вектор, який має напрям
а
, якщо λ додатне, і
протилежний напрям, якщо λ від'ємне; довжина цього вектора дорів-
нює добутку вектора
а
на абсолютне значення (модуль) числа λ.
Добуток вектора
а
на число λ позначається
а
λ
. Якщо
а
= 0
або λ = 0, відповідно вважають:
00
=
⋅
λ
для будь-якого λ ,
0а0 =⋅
для будь-якого
а
.
Властивості операції множення вектора на число:
1) комутативність: λ
а
=
а
λ;
2) асоціативність:
а)()а( ⋅℘=℘
λλ
;
3) дистрибутивність:
bа)bа(
λλλ
+=+
;
ааа)( ℘+=⋅℘+
λλ
.
Два ненульові вектори називають колінеарними, якщо їхні на-
прями збігаються або протилежні.
Пряма
l
із заданим на неї напрямом, яке приймається за додат-
не, зветься віссю
l
.
Проекція вектора
а
на вісь
l
це число, яке позначається
l
пр а
a
b
–b
c = a–b
B
C
A
–b
a
c = a–b
Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
88
і дорівнює
ϕ
cos|а| ⋅
, де
ϕ
(
π
ϕ
≤
≤
0
) - кут між додатним напрямом
вісі
l
та напрямом вектора
а
, тобто за визначенням
l
пр
ϕ
cos|а|а =
.
Геометрично проекцію вектора
а
можна визначити довжиною
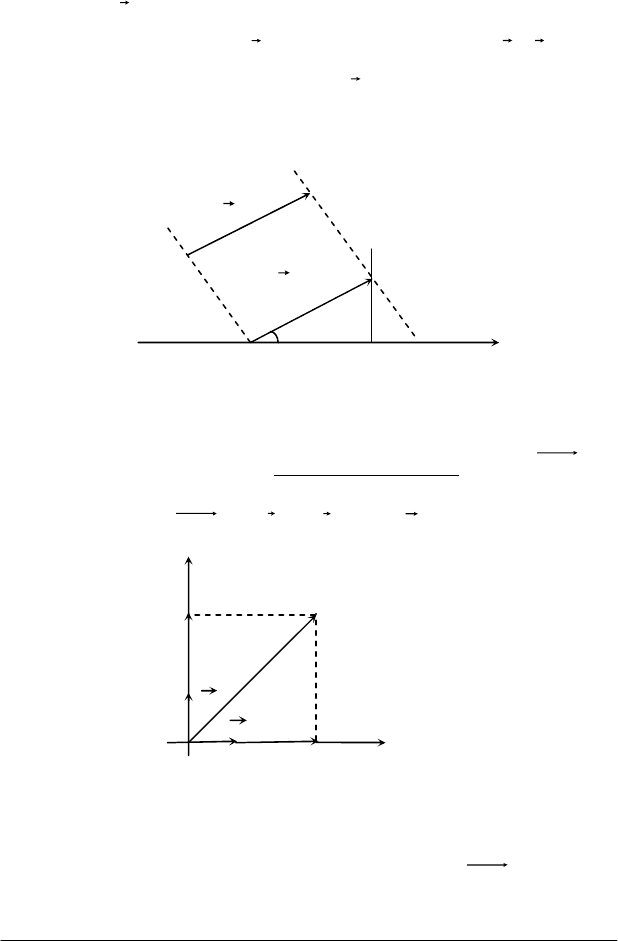
відрізка MN (рис.4.5), яка береться із знаком "+", якщо
2/0
π
ϕ
≤
≤
, та
із знаком "–", якщо
π
ϕ
π
≤
≤
2/
.
Рис. 4.5
Координати вектора. На координатній вісі вектор
0
ОМ
має
координату х
0
і записується так:
ехОМ
00
⋅=
, де
е
- орт,
1| e| =
.
Рис. 4.6
На координатній площині (рис. 4.6) вектор
0
ОМ
є діагональ
прямокутника ОМ
1
М
0
М
2
і, якщо
1 0
ОМ х i
= ⋅
uuuuur ur
;
2 0
ОМ у j
= ⋅
uuuuur r
, то за пра-
y
E
2
x
E
1
M
2
M
1
M
0
(x
0
,y
0
)
j
i
ℓ
φ
а
N
а
M
0
Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
89
вилом паралелограма запишемо:
jуi хОМОМОМ
00210
⋅+⋅=+=
це
розклад вектора у заданому базисі
i
,
j
, де
i j 1
= =
, на складові век-
тора. Тобто вектор
0
ОМ
має координати х
0
та у
0
і записують
)у;х(ОМ
000
=
. Модуль вектора
0
ОМ
, буде обчислюватись за фор-
мулою:
2
0
2
00
ух|ОМ| +=
.
Відстань між довільними точками А і В на площині, які мають
відповідно координати (х
1
;у
1
) і (х
2
;у
2
) обчислюють за формулою:
( ) ( )
2
12
2
12
ууххАВ −+−=
.
За цією ж формулою обчислюють довжину вектора
АВ
uuur
, який
має ті ж координати:
( ) ( )
jуу iххАВ
1212
⋅−+⋅−=
.
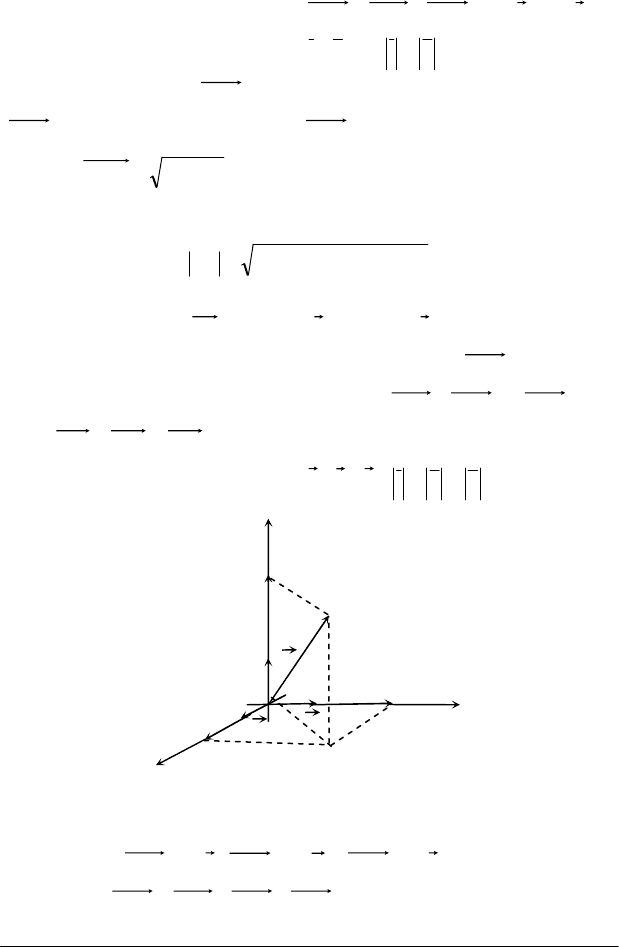
У координатному просторі (рис. 4.7) вектор
0
ОМ
є діагональ
паралелепіпеда, який утворено на векторах
1
ОМ
,
2
ОМ
, і
3
ОМ
; век-
тори
1
ОЕ
,
2
ОЕ
,
3
ОЕ
є базисними векторами (ортами) прямокутної
системи координат їх позначають:
і
,
j
,
k
;
i j k 1
= = =
.
Рис. 4.7
Отже:
іхОМ
01
=
;
jуОМ
02
=
;
kzОМ
03
=
. За правилом пара-
лелепіпеда
3210
ОМОМОМОМ ++=
, це розклад вектора по трьом
z
E
3
x
M
3
M
2
M
0
(x
0
,y
0
,z
0
)
k
i
y
E
2
z
0
0
E
1
x
0
M
1
y
0
j
