Станішевський С.О. Вища математика. Конспект лекцій. Модуль 1
Подождите немного. Документ загружается.


Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
90
складовим векторам. У заданому базисі:
kzjу іхОМ
0000
++=
. Тобто,
вектор
0
ОМ
, має координати х
0
; у
0
; z
0
, що записують
0
ОМ
=(х
0
; у
0
; z
0
). Довжина (модуль) вектора
0
ОМ
обчислюється за формулою
2
0
2
0
2
00
zух|ОМ| ++=
.
Відстань між точками А(х
1
; у
1
; z
1
) і В(х
2
; у
2
; z
2
) обчислюють за
формулою
( ) ( ) ( )
2
12
2
12
2
12
zzууххАВ −+−+−=
. (4.1)
За цією ж формулою обчислюють і
|АВ|
, який має відповідні коорди-
нати:
( ) ( ) ( )
kzzjуу іххАВ
121212
⋅−+⋅−+⋅−=
.
Розклад вектора за трьома некомпланарними векторами. Нехай
с ,b ,а
- три некомпланарні (не лежать у одній площині) ненульові
базові вектори. Тоді будь-який просторовий вектор
d
єдиним чином
можна записати у вигляді суми:
сzbуахd ⋅+⋅+⋅=
.
Доведення. Нехай існує другий розклад:
сzbуахd
111
⋅+⋅+⋅=
.
Ліворуч один і той же вектор, тому:
сzbуахсzbуах
111
⋅+⋅+⋅=⋅+⋅+⋅
або
0с)zz(b)уу(а)хх(
111
=⋅−+⋅−+⋅−
. Але
0|с|і 0|b| ,0|а| ≠≠≠
Тотожність можлива, якщо
0zz ;0уу ;0хх
111
=−=−=−
. Звідси ма-
ємо:
111
zz ;уу ;хх ===
. Тобто, розклад єдиний.
Добутки векторів. Скалярний добуток. Скалярним добутком
двох ненульових векторів
а
і
b
, який позначають (
а
,
b
), або
⋅а b
, є
число, що дорівнює добутку довжин векторів на косинус кута між ни-
ми: (
а
,
b
)=
ϕ
cos|b||а| ⋅⋅
, де
) b ,а(
∧
=
ϕ
- кут між векторами
а
і
b
.
Властивості скалярного добутка векторів:
- комутативність (
а
,
b
) = (
b
,
а
);
- асоціативність
)b,а(k)b),аk(( ⋅=⋅
;
- дистрибутивність
)с,а()b,а())сb(,а( +=+
;

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
91
- скалярний добуток
2
|а|аа =⋅
.
Якщо хоча б один з двох векторів нульовий, або вектори
а
і
b
перпендикулярні один до одного, то скалярний добуток дорівнює ну-
лю.
Векторний добуток. Векторним добутком двох векторів
а
і
b
є
вектор
с
r
, який позначають [
а
,
b
] =
с
r
, або
а
×
b
=
с
r
, який визна-
чається такими трьома умовами:
- він перпендикулярний як до вектора
а
, так і до вектора
b
;
- упорядкована трійка векторів (
а
;
b
;
с
), відкладених від одні-
єї точки, утворює правий (у загальному випадку косокутний)
базис;
- модуль вектора |
с
|
=
ϕ
sin|b||а| ⋅
, де
j
- кут між векторами
а
і
b
, чисельно дорівнює площі паралелограма побудованого на
векторах
а
r
і
b
r
.
Властивості векторного добутку:
- зміна місць множників дає протилежний вектор
]а ,b[]b ,а[ −=
;
- асоціативність
]b ,а[k]b ),а k[( =
;
- дистрибутивність
]с ,b[]с ,а[]с ),b а[( +=+
.
Якщо хоча б один з векторів нульовий, або вони колінеарні
(
π
ϕ
ϕ
=
=
;0
), то їх векторний добуток дорівнює нульовому вектору.
Мішаний (скалярно-векторний) добуток трьох векторів. Міша-
ним добутком трьох некомпланарних векторів є число, абсолютна ве-
личина якого дорівнює об'єму паралелепіпеда з ребрами
а
,
b
,
с
, які
відкладені від однієї точки.
Мішаний добуток векторів
а
;
b
;
с
позначають
(
а b с )
r r r
. Якщо
вектори
а
,
b
,
с
компланарні, то мішаний добуток дорівнює нулю.
ЛЕКЦІЯ № 18
Правила дій над векторами, заданими координатами. Якщо у

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
92
прямокутній системі координат Oxyz точки А і В мають координати (х
1
,
у
1
, z
1
) і (х
2
, у
2
, z
2
), то координатами вектора
АВ
буде трійка чисел (x
2
–
x
1
;y
2
– у
1
;z
2
– z
1
), тобто
АВ
= (x
2
– x
1
;y
2
– у
1
;z
2
– z
1
), або
АВ
=
k)zz(j)уу( і)хх(
121212
⋅−+⋅−+⋅−
. Вектори
, а
, b
і
, с
у базисі
(
k ,j , і
) задані своїми координатами:
= а
(х
1
, у
1
, z
1
);
= b
(х
2
, у
2
, z
2
);
= с
(х
3
, у
3
, z
3
).
Тоді: довжину вектора
а
r
обчислюємо за формулою (4.1);
- координати суми (різниці) двох векторів дорівнюють сумі (рі-
зниці) відповідних координат доданків
)zz ,уу ,хх( b а
212121
±±±=±
;
- координати добутку вектора на число дорівнюють добутку ві-
дповідних координат даного вектора на це число
;
1 1 1
а ( х ; у ; z )
λ λ λ λ
=
uur
- скалярний добуток двох векторів дорівнює сумі добутків від-
повідних координат цих векторів
212121
z zуу хх) b, а( ⋅+⋅+⋅=
. (4.2)
Доведення.
=++⋅++= )kzjу iх ()kzjу iх() b, а(
222111
+⋅++⋅+⋅+⋅+= k jz уjуу i jху k iz хj iух iхх
21
2
21
2
212121
2
21
.z zуу хх kz zjkуz ikхz
212121
2
212121
++=⋅+⋅+⋅+
Тут:
,0kj ,0k i ,0j i =⋅=⋅=⋅
а
1k ,1j ,1 i
222
===
;
- векторний добуток двох ненульових векторів
а
і
b
, заданих
своїми координатами, є вектор
с
, який обчислюємо з визначника тре-
тього порядку
;
zух
zух
kj i
с
222
111
=
або
=
22
11
22
11
22
11
ух
ух
,
хz
хz
,
zу
zу
с
, (4.3)
де координати вектора
с
є визначниками другого порядку.
Доведення
.
1 1 1 2 2 2
[
а ,b ] [ х i у j z k, х i у j z k ]
= + + + + =
uur uur ur r r ur r r
Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
93
1 2 1 2
х х [i , i ] х у [i , j]
= + +
ur ur ur r
++++++ ]і ,k[хz]k ,j[zу]j ,j[уу] i ,j[хy]k , i[zх
2121212121
=−++−−=++ iуzjхzі zуkхуjzхkух]k ,k[zz]j ,k [уz
2121212121212121
=−+−−−= k)хуух(j)хzzх( i)уzzу(
212121212121
.с
zух
zух
kj i
k
ух
ух
j
хz
хz
i
zу
zу
222
111
22
11
22
11
22
11
==⋅+⋅+⋅=
Тут:
;0] і, і[ =
;0]j,j[ =
;0]k,k[ =
;k]j, і[ =
; i]k,j[ =
;j] i,k[ =
;k] i,j[ −=
; і]j,k[ −=
;j]k, i[ −=
- мішаний добуток векторів
а
,
b
, і
с
, заданих своїми координа-
тами, обчислюють як визначник третього порядку
(ab
с )
rrr
=
333
222
111
zух
zух
zух
. (4.4)
Трійка векторів
а
,
b
, і
с
може утворювати новий базис, якщо
їх мішаний добуток не дорівнює нулю;
- косинус кута
ϕ
між двома ненульовими просторовими векто-
рами
а
і
b
, заданими своїми координатами, обчислюємо з рівності
cos cos(
а,b ) (а b )/(|а | |b|)
ϕ
∧
= = ⋅ ⋅ =
r r r r r r
2 2 2 2 2 2
1 2 1 2 1 2 1 1 1 2 2 2
(
х х у у z z )/( х у z х у z )
= + + + + ⋅ + +
; (4.5)
- косинуси кутів α, β, γ між вектором
а
і векторами базису
і
,
j
,
k
мають назву "напрямні косинуси", їх обчислюємо за формулами:
|а|/xcos
1
=
α
;
|а|/уcos
1
=
β
;
|а|/zcos
1
=
γ
(4.6)
- напрямні косинуси будь-якого ненульового вектора
а
зв'язані
рівністю
Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
94
1coscoscos
222
=++
γβα
, що безпосередньо випливає з їх визначен-
ня.
Приклад. Піраміда має вершини у точках А(–2;–5;–1), В(–6; –7;
9), С(4;–5;1) і D(2;1;4). Знайти:
а) косинус кута ADB;
б) площу грані АВС;
в) об'єм піраміди.
Розв'язання. а) косинус кута ADB знайдемо за формулою (4.5).
Для цього побудуємо вектори
DA
і
D
В
:
k5j6 і4k)14(j)51( і)22(DA −−−=⋅+−⋅+−⋅+−=
;
k5j8 і8k)49(j)17( і)26(DВ ⋅+⋅−⋅−=⋅−+⋅+−⋅+−=
.
Тоді
=⋅= |)DB||DA/(|)DBDA(cos
ϕ
⋅−+−+−⋅−+−⋅−+−⋅−=
222
)5()6()4(/()5)5()8()6()8()4((
=++⋅++−+=+−+−⋅ )256464253616/()254832()5)8()8(
222
51,015377/55 ≈⋅=
.
б) площа грані АВС є площа трикутника:
АВС
S 0,5 [
АВ,АС ] 0,5 | АВ | | АС | sin( AВ,АС )
∆
∧
= ⋅ = ⋅ ⋅
uuur uuur uuur uuur uuur uuur
.
Побудуємо вектори
АВ
і
АС
:
k10j2 і4k)19(j)57( і)26(AВ +−−=⋅++⋅+−+⋅+−=
;
k2 і6k)11(j)55( і)24(AС +=⋅++⋅+−+⋅+=
.
Площа трикутника дорівнює половині площі паралелограма,
який побудовано на векторах
АВ
і
АС
, а довжина вектора
АВ, АС
uuur uuur
чисельно дорівнює площі цього ж паралелограма. Третя
умова векторного добутку двох векторів.
Тоді:
[
АВ
,
АС
] =
=
−−
⋅+
−
⋅−
−
⋅=−−
06
24
k
26
104
j
20
102
i
206
1024
kj i

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
95
с k12j68 і4 =++−=
.
=++=++−= 14446241612684)( |с|
222
4784 69,17
= ≈
;
6,34S
АВС
≈
∆
од. кв.
в) Об'єм піраміди дорівнює одній шостій об'єму паралелепіпеда,
який побудовано на трьох векторах:
АD
,
ВD
,
СD
, і обчислюється за
допомогою мішаного добутку (4.4). Побудуємо ці вектори:
k5j6 і4k)14(j)51( і)22(AD ++=⋅++⋅++⋅+=
;
k5j8 і8k)94(j)71( і)62(ВD −+=⋅−+⋅++⋅+=
;
k3j6 і2k)14(j)51( і)42(СD ++−=⋅−+⋅++⋅−=
.
(
АD
,
ВD
,
СD
,) =
452144120802406096
362
588
564
=−++++=
−
−
.
Таким чином,
6
452
V
АВСD
=
од.куб. =
3
1
75
од.куб.
Приклад. Довести, що вектори:
а (3; 1;0 )
= −
r
;
b
=(2;3;1), і
с ( 1;4;3)
= −
r
утворюють базис. Знайти розклад вектора
)7;3;2(d =
у
цьому базисі.
Розв'язання. Якщо
(
а, b, с) 0
≠
r r ur
, то вектори
а
,
b
і
с
утворюють
базис. Перевіримо це:
3 1 0
(
а, b ,с ) 2 3 1 27 1 6 12 22.
1 4 3
−
= = + + − =
−
r r r
Отже,
(
а, b ,с ) 0
≠
r r r
. Дані вектори утворюють базис.
Розклад вектора
d
має вигляд:
сzbуахd ++=
, де х, у, z - неві-
домі числа. Векторне рівняння перепишемо у вигляді системи трьох
лінійних рівнянь з трьома невідомими х, у і z:
3
х 2у z 2,
х 3у 4z 3,
у 3z 7.
+ − =
− + + =
+ =
Розв'яжемо систему за методом Крамера. Головний визначник

Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
96
цієї системи обчислено вище:
з
22
∆
=
.
Допоміжні визначники
х
∆
,
у
∆
і
z
∆
- дорівнюють:
66
317
433
122
х
=
−
=
∆
;
44
370
431
123
у
−=−
−
=
∆
;
66
710
331
223
z
=−=
∆
;
322/66/х
3
х
===
∆∆
;
222/44/у
3
у
−=−==
∆∆
;
322/66/z
3z
===
∆∆
.
Таким чином:
с3b2а3d +−=
.
ТЕМА 5. АНАЛІТИЧНА ГЕОМЕТРІЯ У ПРОСТОРІ
ЛЕКЦІЯ № 19
Прямокутна система координат у просторі.
Нехай
α
- деяка площина у просторі з узятою на ній прямокутною
системою координат Оху (розглянуто у аналітичній геометрії на пло-
щині). Проведемо через точку О пряму, яку позначимо Оz, перпенди-
кулярну до площини
Оху
(рис. 4.7). Візьмемо на прямій Оz напрям і
масштабний відрізок ОЕ
3
, який дорівнює відповідно масштабним від-
різкам ОЕ
1
і OE
2
координатних вісей Ох і Оу. Пряма Oz - третя коор-
динатна вісь. Таким чином, прямокутною системою координат у прос-
торі називають упорядковану трійку взаємно перпендикулярних коор-
динатних осей Ох, Оу і Oz. Вісь Ох називають віссю абсцис, вісь Оу -
віссю ординат, вісь Оz - віссю аплікат. Площини Оху, Oxz, Oyz - нази-
вають координатними площинами; тривимірний простір, у якому уве-
дено систему координат, називають координатним.
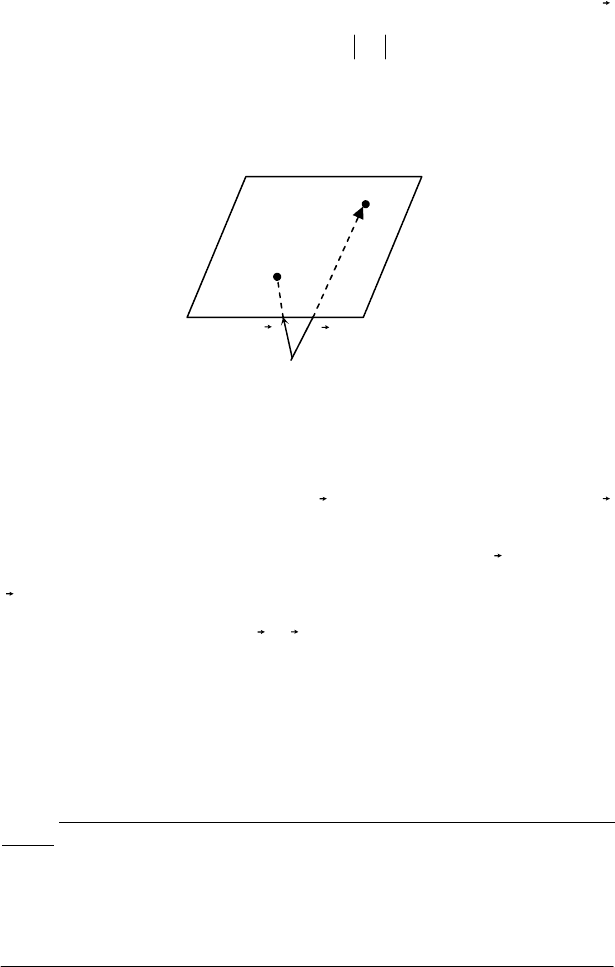
Площина. Нормальне рівняння площини. Положення площини
у просторі буде повністю визначено, якщо задати її відстань р від по-
чатку координат О, тобто довжину перпендикуляра ОТ, який опущено
з точки О на площину, та одиничний вектор
е
r
на ньому, (рис.5.1).
Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
97
Нехай точка M(x,y,z) довільна точка площини, її радіус-вектор
r
змінюється так, що весь час
е
Пр ОМ ОТ р
= =
r
uuuur
. Ця умова має місце
лише для точок площини; воно не виконується, якщо точка М не
лежить на площині. Отже, маємо властивість точок площини, яку
запишемо у векторній формі:
е
Пр ОМ r e р
= ⋅ =
r
uuuur r r
(5.1)
Рис. 5.1
Рівняння (5.1) висловлює умову, за якої точка Μ лежить на
даній площині, і має назву нормального рівняння площини. Воно
записано у векторній формі. Вектор
r
має координати х, у, z. Вектор
е
своїми проекціями має косинуси кутів α, β, γ, які він утворює з
координатними вісями Ох, Оу та Oz. Тобто,
( )
z ;у ;хr =
i
( )
γβα
cos ;cos ;cosе =
.
Скалярний добуток векторів
r
і
е
дає нормальне рівняння площини у
координатній формі:
0рcoszcosуcosх
=
−
+
+
γ
β
α
. (5.2)
Рівняння (5.2) - першого степеня відносно x, у, z, тобто всяка площина
може бути подана рівнянням першого порядку відносно поточних
координат.
Зведення загального рівняння площини до нормального виду
(5.2). Вище було доведено, що будь-яка площина може бути подана
рівнянням першого порядку. Доведемо зворотне: будь-яке рівняння
першого порядку (степеня) між трьома змінними визначає площину.
Візьмемо рівняння першого степеня загального вигляду:
Ах + Ву + Cz + D = 0, (5.3)
r
T
M(x,y,z)
O
е
Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
98
де
0
СВА
222
≠++
. Розглядатимемо А, В і С як проекції на вісі
координат Ох, Оу і Oz деякого вектора
N
, а х. у, z як проекції радіус-
вектора
r
точки Μ. Тоді рівняння (5.3) має вигляд
0DNr =+⋅
, (5.4)
яке зводиться до (5.1), якщо останнє розділити на
N
uur
. Тобто,
матимемо:
|N|/N
е
=
і
|N|/D
р
−=
, де
2 2 2
N
А В С
= + +
uur
.
Таким чином, рівняння (5.4) завжди може бути зведено через
рівняння (5.1) до нормального вигляду (5.2). Але нормальне рівняння
(5.2) завжди визначає площину. Отже, рівняння (5.4), відповідно, і
початкове рівняння (5.3), визначає площину, що й треба було довести.
З попереднього маємо спосіб перетворення загального рівняння
(5.3) площини до рівняння (5.2) площини у нормальній формі: щоб
привести загальне рівняння (5.3) першого степеня до нормального
вигляду треба помножити його на:
2 2 2
М 1/ А В С 1/ N
= ± + + = ±
, (5.5)
де знак множника належить брати протилежним знаку вільного члена
D. Цей множник має назву нормуючого множника.
Після множення на Μ рівняння (5.3) матиме вигляд:
0МDМСzМВуМАх
=
+
+
+
і співпадає з (5.2), якщо:
рМD ;cosМС ;cosМВ ;cosМА
−
=
=
=
=
γ
β
α
.
Звідси маємо формули для обчислення напрямних косинусів і числа р:
cos A/|N|
α
=
uur
;
cos
В /|N|
β
=
uur
;
cos
С /|N|
γ
=
uur
;
р D /|N|
− =
uur
(5.6)
З останнього маємо:
1coscoscos
222
=++
γβα
. (5.7)
Приклад. Рівняння площини
3z2у2х
=
+
−
перетворити до
нормального вигляду.
Розв'язок. Обчислимо нормуючий множник
( ) ( ) ( )
3/19/1221/1М
222
==+−++=
.
Помножимо на нього дане рівняння. Маємо:
(
)
(
)
(
)
1/ 3
х 2 / 3 у 2 / 3 z 1 0
× − + − =
.
Для даної площини: cosα = 1/3; cosβ = –2/3; cosγ = 2/3; p = 1.
Дослідження загального рівняння площини.
Подивимось, які
часткові положення відносно системи координат Охуz займає площина
Вища математика
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
99
Ах + Ву + Cz + D = 0,
якщо деякі коефіцієнти цього рівняння дорівнюють нулю:
а) D = 0. Ах + Bу + Cz = 0 - площина, яка проходить через
початок координат;
б) А = 0, або В =0, або C = 0. Тобто коефіцієнт біля однієї з
змінних дорівнює нулю. Наприклад, А = 0. Ву +Cz +D = 0. Це
площина, яка паралельна вісі Ох. У другому і третьому випадках
маємо площини, які паралельні вісям Оу і Oz відповідно;
в) D = 0; А = 0, або В = 0, або C = 0. Тобто, коефіцієнти біля
однієї з змінних та вільний член дорівнюють нулю. Наприклад, А = 0 і
D = 0. Ву + Cz = 0. Це площина, яка містить вісь Ох. У другому і
третьому випадках маємо площини, які містять вісі Оу і Oz відповідно;
г) коефіцієнти біля двох змінних дорівнюють нулю. Наприклад,
А = 0 і B = 0. Маємо Сz + D = 0. Це рівняння площини, яка паралельна
координатній площині xOy. Якщо А = 0 і С = 0, або В = 0 і С = 0
будемо мати площини, які паралельні координатним площинам xOz і
уОz відповідно;
д) коефіцієнти біля двох змінних і вільний член дорівнюють
нулю. Наприклад, А = 0, В =0 і D = 0. Маємо Cz = 0.
≠
С
0, тоді z = 0 -
рівняння координатної площини уОх. Якщо А = 0, С = 0 i D = 0 або В
= 0, C = 0 і D = 0, матимемо відповідно рівняння координатних
площин xOz і yOz.
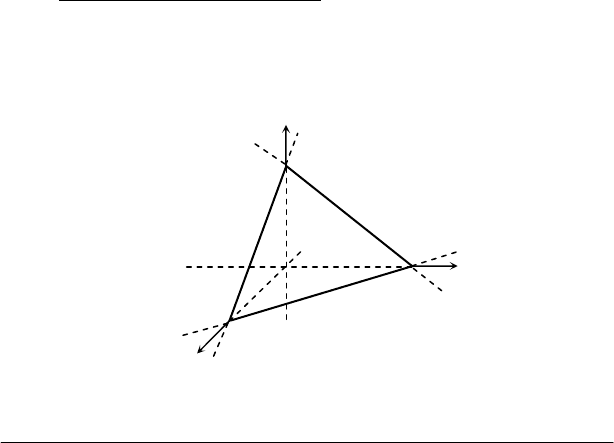
Рівняння площини у відрізках. Розглянемо площину
Ах + Ву + Cz + D = 0, яка перетинає всі три координатні вісі. З
попереднього відомо, що у цьому випадку жоден з коефіцієнтів не
дорівнює нулю. Позначимо через а, b і с довжини відрізків, які відсікає
площина на вісях координат (рис.5.2).
Q(0;b;0)
Рис. 5.2
z
y
x
0
c
a
b
R(0;0;c)
P(a;0;0)
