Stacey F.D., Davis P.M. Physics of the Earth

Подождите немного. Документ загружается.

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C14.3D

–

207

– [197–223] 13.3.2008 12:37PM

planes. In directions at  to this, third plane the

amplitude of motion is diminished by the factor

cos  and there is no P-wave radiation in either

of the nodal planes. Figure 14.9(c) gives a three-

dimensional perspective.

In the Earth, seismic waves are refracted

by the velocity variations and so there are cor-

responding refractions of the nodal planes. By

allowing for these refractions, first motions

observed at widely scattered stations are used to

deduce the nodal planes of well-observed earth-

quakes and the directions of slip. The results are

known as fault plane solutions, or focal mecha-

nisms. The coverage of the Earth with reliable

seismic stations suffices to allow focal mech-

anisms to be determined routinely for all large

earthquakes and many smaller ones. They dem-

onstrate that the movements are all contribu-

tions to the grand pattern of global tectonics

and they are used to study local details of the

pattern.

Without further information, the two nodal

planes are indistinguishable. As we concluded

from Eq. (14.15), this is a consequence of the dou-

blecouplenatureofearthquakes.Thepictorial

representation of focal mechanisms is the pro-

jection onto a horizontal plane of black (com-

pression) and white (rarefaction) quadrants for

downgoing waves, that is P waves into a hemi-

sphere below the source. Figure 14.10 gives

three simple examples. While this representa-

tion incorporates the ambiguity in t he nodal

planes, the directions of compressive and ext-

ensional stress are not ambiguous and the

pattern of movement is often evident in a

plot showing several fault plane solutions for

earthquakes in a limited area.

There are several methods by which fault

planes may be distinguished from auxiliary

planes. Extended faults of large earthquakes

are often outlined by foci of aftershocks. The

direction of motion may be indicated by obser-

vations of surface displacements or by asym-

metries in the wave patterns. If an earthquake

is unilateral in the sense that the fault break

propagates strongly in one direction from its

initiation, but hardly at all in the opposite

direction, then the amplitude of the first pulse

of the P-wave train is greater in the direction

of propagation but its duration is shorter. The

radiation pattern departs from the symmetry of

Fig. 14.9(b) and the ambiguity of a conventional

fault plane solution is then resolved. We exam-

ine this phenomenon, called ‘directivity’, in the

next section.

First motion studies have generally empha-

sized P waves, but S waves give complementary

information. In this case the motion is perpen-

dicular to the radius from a source, and has both

 and  components, where  is the angle in

the plane of Fig. 14.9(b) and  is the angle with

respect to this plane. Using unit vectors



and

, as in Aki and Richards (2002), the P

(radial) and S (tangential) first motions are pro-

portional to

¼ sin 2 cos 

r for P waves; (14:17)



¼ cos 2 cos 





¼cos  sin 





for S waves: (14:18)

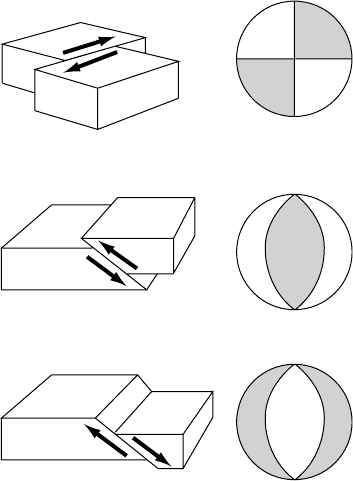
(a)

(b)

(c)

FIGURE 14.10 Focal mechanisms for earthquakes on

(a) a transcurrent fault with no vertical movement, (b) a

thrust fault, of the kind occurring in subduction zones,

and (c) a normal fault. The ‘beachball’ representation of

first motions shows the quadrantal pattern as seen from

below the faults, with shading for initial compressions.

14.4 FIRST MOTION STUDIES 207

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C14.3D

–

208

– [197–223] 13.3.2008 12:37PM

14.5 Rupture models and the

spectra of seismic waves

In this section we integra te the dynamic Green’s

function to show some relationships used to

interpret seismograms, in particular the esti-

mation of seismic moments from the low-

frequency spectra of seismic waves. A point

source, that is, one with infinitesimal dimen-

sions an d rupture time, would giv e rise to a

white spectrum. Finiteness of the rise time of

slip and the fault dimen sions of a real source

cause the white spectrum ideal to be truncated

at high freq uencies, but the low frequency

range of the spectrum is white. This requires

the frequency range considered to be very low,

relative to the slip duration, and to correspond

to wavelengths much greater than the fault

dimension, so that the source is indistinguish-

able from a point.

We examine a rectangular fault model with

rupture propagating at a fixed velocity, less

than the S-wave speed. The rupture moves

from one end of the fault to the other, with

rupture occurring on a slipping patch, with a

rupturing edge and a healing edge a fixed dis-

tance apart. The waves in the direction of rup-

ture tend to have higher frequencies than those

measured in the opposite direction because

the source of radiation is moving in the direc-

tion of wave propagation, causing the energy

to ‘pile up’ and give a shorter, more intense

pulse. In the opposite direction the source is

receding and so t he waves become drawn out

as the rupture front recedes. This is a seismo-

logical Doppler effect.

Equation (14.8) gives the static Green’s func-

tions that can be used in Eq. (14.13). Integration

over a two-dimensional strike-slip fault gives

Eq. (14.5). The Green’s function for a dynamic

point force is quite complicated, with near,

intermediate and far field terms, but is sim-

plified by considering the far field only. In a

medium with P and S wave speeds V

and V

the far field displacement caused by a fault patch

is given by



’

4prV

ðt  r=V

4prV

ðt  r=V



’

; ð14:19Þ

where

is the rate of change of the moment

tensor associated with the patch. Equation (14.19)

has the general form

u ¼

4pV

ðt  r=VÞ; (14: 20)

where V is V

or V

and R

is the P or S wave

radiation pattern (Eq. (14.17) or (14.18)). We take

the Fourier transform of Eq. (14.20),

uð!Þ¼

4pV

1

ðt  r=VÞexpði!tÞdt:

(14:21)

Let  ¼t r/V. Then

uð!Þ¼

4pV

expði!r=VÞ

1

ðÞexpð i!Þd:

(14:22)

We are interested in the asymptotic value of

Eq. (14.22) as ! !0. The integral term becomes

¼ M

. Then

uð! ! 0Þ¼

4pV

expði!r=VÞ: (14:23)

This illustrates the important result that the dis-

placement spectrum of far-field P and S seismo-

grams at ! !0 can be used to obtain the total

moment. Equation (14.22) shows that, if the

moment rate is a delta function, the spectrum

is flat (white) for all frequencies. A more realistic

case is a boxcar function of duration T,asin

Fig 14.11(a), between T/2  T/2. If the slip is

D over area A,

M ¼ AD=T so that Eq. (14.22)

becomes

208 KINEMATICS OF THE EARTHQUAKE PROCESS

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C14.3D

–

209

– [197–223] 13.3.2008 12:37PM

uð!Þ¼

4pV

expði!r =VÞ

T=2

T=2

expði!Þd

4pV

expði!r =VÞsinð!T=2Þ=ð!T=2Þ

4pV

expði!r =VÞsincð!T=2Þ: ð14:24Þ

The finite rise time gives a 1/! displacement

spectrum at high frequencies.

To model displacements from a propagating

break of a finite fault we integrate Eq. (14.20).

Consider a long thin fault of width W and length

L (Fig. 14.11(b)), for which rupture starts at one

end and progresses to the other end at constant

speed, V

. This is the rupture velocity, which, for

many earthquakes is found to be 0.7 to 0.9 times

the S-wave speed. At any given location, once the

slip starts, it rises to its final value D, which could

be 1 m, in time T, and then remains constant. T is

referred to as the rise time and is generally a few

seconds. Thus the slip velocity, that is, the speed

of the material in the fault face, is metres per

second, compared with the rupture velocity,

which is several kilometres per second. We can

think of this as a wave, with particle motion

much slower than the advance of the wave.

This is the simplest finite fault model, referred

to as the ‘Haskell model’, recognizing its origi-

nator, Norman Haskell, who also solved the iso-

static rebound problem (Chapter 9). The Haskell

model has five parameters, fault dimensions of

length L, width W, slip D, rise time T and rupture

velocity V

. It has an active slipping patch

that starts slipping at –L /2 at t ¼0 (Fig 14.11(b)).

It builds up to a constant size W (T V

) and

sweeps from one end to the other at the rupture

velocity, rather like dominos falling in a line,

with the ones falling at any instant representing

the patch.

Consider an element of the moving patch

with dimensions Wdy at y. Then d

¼ 

DWdy.

The radiation from this element arrives at a dis-

tant point, P (Fig. 11.4(b)), at time t that is the sum

of the rupture time, (L/2 þy)/V

, and travel time,

R/V. We integrate over the whole fault, taking

into account the fact that

D is non-zero only

during the period of slip of the element. This

can be represented by writing

D, as a function

of time, as

DtðL=2 þ yÞ=V

 R=V½, over the

duration of patch slip. Then

u ¼

W

4pV

L=2

L=2

DtðL=2 þ yÞ=V

 R=V½dy:

(14:25)

In the far field, r L W, R ¼r y cos w, and for

the purpose of the 1/R term in Eq. (14.25), r R

and 1/R can be taken outside the integral.

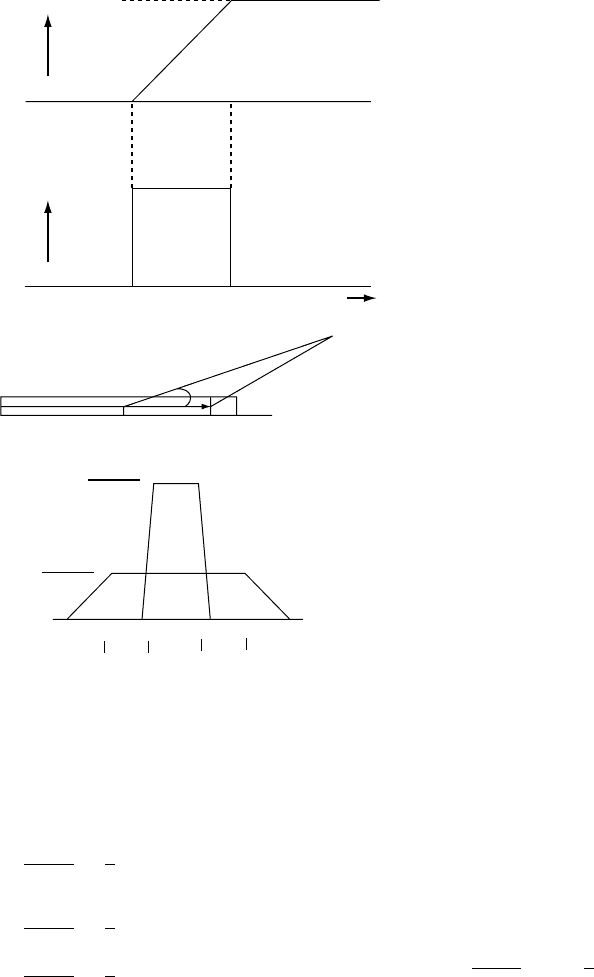
Equation (14.25) becomes

Time–T/2

T/2

Moment rate Fault slip

slip = Dt

0 L

/2–L /2

forward

backward

+ L /V

0 L

+ TL / V

L /V

+ L / V + T

(a)

(b)

(c)

L /V + T

/ V

L /V

– L /V

+ L /V

FI G U R E 14.11 A fault model for calculation of the

radiation pattern from an earthquake. (a) Variation of

moment and moment rate with time. (b) Finite fault for

the Haskell (1969) calculation. (c) Resulting seismic

pulses.

14.5 RUPTURE MODELS AND THE SPECTRA OF SEISMIC WAVES 209

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C14.3D

–

210

– [197–223] 13.3.2008 12:37PM

u ¼

W

4pV

L=2

L=2

D ½t  r=V ðL=2 þ yÞ=V

þ y cosw=Vdy ¼

4pV

PðtÞ; ð14:26Þ

where the seismic pulse shape P(t) is a character-

istic of the source and the other terms refer to

propagation of the waves. Recalling that

D ¼ D=T

and M

¼mWLD, we have

PðtÞ¼

L=2

L=2

Itr=V ðL=2 þ yÞ=V

þ y cosw=V½dy;

(14:27)

where I[t] ¼1 for 0 t T. Integration of (14.27)

gives a pulse that has the shape of a trapezoid

(Fig. 14.11(c)), with high amplitude, short dura-

tion and rise time in the direction of rupture and

lower amplitude, longer rise time and duration

in the opposite direction (Problem 14.6). The area

of each trapezoid is equal to M

for all w. This is

the source function and the observed pulses are

modulated by propagation effects, including the

radiation pattern (Eqs. (14.17) and (14.18)). An

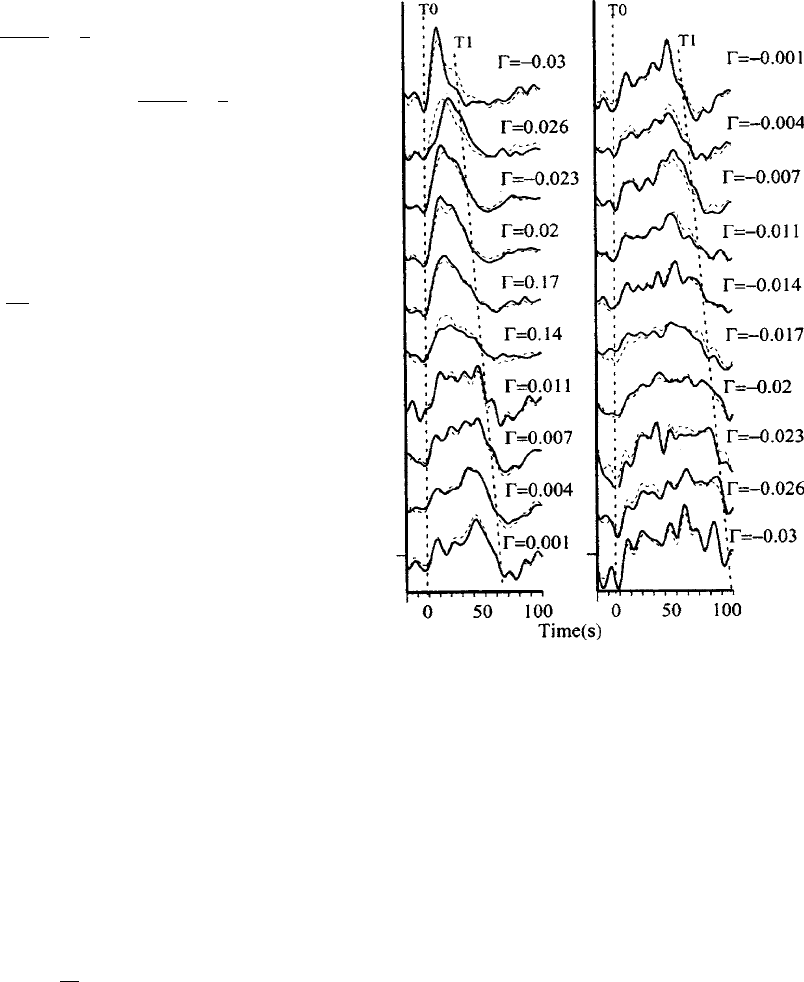
example of this directivity is seen in the pulses

observed at different azimuths from 1995 Colima-

Jalisco, Mexico M

8 earthquake (Courboulex

et al., 1997) in Fig. 14.12. From the sharpness of

west-bound pulses and the longer duration of the

southbound pulses we see that this event propa-

gated in a northerly direction.

In order to investigate the frequency depend-

ence of Eq. (14.27) we take the Fourier transform,

with a change of variables t ¼ r/V (L/2 þy)/

þy cos w/V and X ¼(1/V

cos w/V)

Pð!Þ¼M

expði!½r=V þT=2 þ L=2=V

Þ

T=2

T=2

expði!Þd

L=2

L=2

expði!XyÞdy;

(14:28)

where dt ¼dt, because the other terms in the

variable substitution are constants. This gives

Pð!Þ¼M

expði!½r=V þT=2 þ L=2=V

Þ

 sincð!T=2Þsinc ð !XL=2Þ: ð14:29Þ

We now have a spectral amplitude that is a pro-

duct of two sinc (sin x/x) functions, resulting from

the finite rise time and finite propagation time,

compared with the single sinc function arising

from the finite rise time in Eq. (14.24). The expo-

nential term is a phase delay and does not affect

amplitudes. The zero-frequency asymptote of

Eq. (14.29) is the moment, while at high frequen-

cies P decays as 1/!

. We see from Eq. (14.29)

and Fig. 14.11 that the amplitude of the pulse

may be written as the convolution of two boxcar

functions.

PðtÞ¼M

1

ðt  ÞB

ðÞd; (14:30)

FI G U R E 14.12 Source time functions at different

azimuths, found by inversion of surface waves from

the 1995 Colima-Jalisco (Mexico) earthquake (after

Courboulex et al., 1997). T0 and T1 are estimated start

and end times. The pulse broadening can be used to

estimate the direction of rupture, N 79

W, average

rupture velocity, 2.8 km/s, and fault length, L ¼150 km.

210 KINEMATICS OF THE EARTHQUAKE PROCESS

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C14.3D

–

211

– [197–223] 13.3.2008 12:37PM

where

ðtÞ¼1=T; 0  t  T;

and

ðtÞ¼1=ðLXÞ; 0  t  LX: (14:31)

The first is associated with the rise time and the

second with the propagation. In the frequency

domain the convolution of two boxcars is the

product of two sinc functions. Since at high fre-

quencies the amplitude of a sinc function decays

as 1/!, the spectrum of the finite fault decays as

1/!

. The cos w term in X gives the ‘forward’ pulse

(in the direction of fault propagation) a greater

high frequency content than the ‘backward’

pulse. At zero frequency the product becomes

unity, which is why the low frequency asymptote

of seismic wave amplitude yields the moment.

As mentioned, if an earthquake is viewed as an

instantaneous point source, its spectrum is white.

A finite rise time introduces a 1/! decay and, as we

see in the above example, a finite spatial extent

adds another 1/! factor. Aki and Richards (2002)

discuss more general cases with two finite fault

dimensions. The extra dimension introduces

another sinc function and therefore another 1/!

term to give a 1/!

spectrum. However, in practice

the 1/!

spectrum gives a better fit to most events,

presumably because propagation time across the

smaller fault dimension is not significant.

Figure 14.13 summarizes the basic features

of seismic spectra. The curves show the dis-

placement spectra for earthquakes of different

magnitudes, magnitude being a measure of

earthquake size, discussed in Section 14.6. Each

curve follows the equation

uð!Þ¼

uð0Þ

1 þð!=!

; (14:32)

where u(!) is the spectral ‘amplitude’ at fre-

quency (! /2p), according to the model of Brune

(1970), and is similar to the double sinc function

of Eq. (14.29). Thus u(!) is the square root of

spectral power per unit frequency interval. f

/2p is termed the corner frequency in the

Brune model and varies systematically with

moment M

. By Eq. (14.29), M

is proportional

to u(0) and the corresponding scale is shown on

the left-hand side of the figure. This figure

illustrates several of the conclusions of the spec-

tral analysis in this section.

(i) The spectra become white (flat) at suffi-

ciently low frequencies, allowing a direct

determination of M

(ii) At the high frequency limit, u(!)variesas

2

. This is the observed general form or

envelope, as the high frequency spectra of

earthquakes are generally irregular, being

complicated by interference phenomena

arising from multiple starting and stopping

events. At the highest frequencies attenua-

tion may be a problem but this does not

obscure the observation that spectral ampli-

tude increases with magnitude or moment

even in the !

2

range. However, large earth-

quakes are observed to radiate more high

frequency energy than the Brune model of

Fig. 14.13 would suggest. This may be attrib-

utable to rapid acceleration and retardation

of slip on small patches of a fault. Fault move-

ment proceeds jerkily as it overcomes stick-

ing points or asperities.

(iii) The corner frequency, f

, which marks the

boundary between low and high frequency

regimes, increases systematically with

decreasing M

. f

is directly related to the

duration of seismic radiation and since, for

constant speed of fault propagation, the

duration is proportional to the linear

dimensions of a fault, it is a direct measure

of fault size. f

is higher for P-waves than

for the slower S-waves.

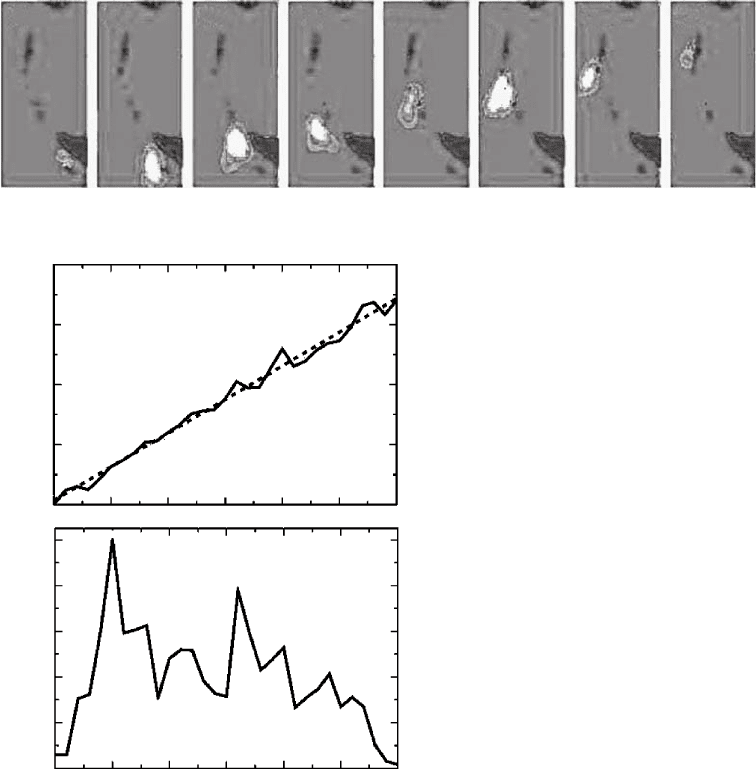
Figure 14.14 shows a sequence of images of

the source of the Sumatra–Andaman earthquake

(Ishii et al. 2005) determined by back-projecting

seismograms from the HiNet array in Japan.

Their analysis indicates a rupture that travelled

1300 km south to north at an average speed of

2.8 km s

1

. Directivity effects were seen at the

very longest wavelengths and also in the azimu-

thal variation of the duration of the high-

frequency body wave seismograms. However, at

the highest frequencies the relative amplitudes

did not exhibit directivity effects, presumably

because the constructive interference necessary

for directivity requires the high-frequency

14.5 RUPTURE MODELS AND THE SPECTRA OF SEISMIC WAVES 211

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C14.3D

–

212

– [197–223] 13.3.2008 12:37PM

sources to be in phase with the propagating

wavefront. While this was seen to be true for

low frequencies, at higher temporal resolution

the wave was erratic, growing and dying in sev-

eral major pulses, as the propagating break

moved northwards. A full description of broad-

band seismic records at high frequencies

requires recognition of the stochastic nature of

the sources (Chapter 15).

14.6 Earthquake magnitude

and energy

Before there were instrumental recordings of

earthquakes, size was reported in terms of the

intensity of local ground shaking with empirical

numerical scales for quantifying it. The most

0.01

0.05 0.1 0.2

0.5

0.001

4.0

5.0

6.0

7.0

8.0

log U

(Nm)

20-second period

(used to define M

)

Corner frequency

for M

= 7

Locus of corner

frequency

Frequency, ω/2π (Hz)

FI G U R E 14.13 Idealized displacement spectra for S waves radiated by earthquakes with a range of magnitudes. The

curves follow Eq. (14.32), giving the spectral amplitude u(!), that is the square root of power per unit frequency

interval (mm per

Hz), as a function of frequency, !/2p. u has a constant value u(0) at ! !

but u(!) / !

2

at ! !

where !

is the corner frequency. This is the

‘!-squared model’ of K. Aki (see Aki and Richards, 2002).

212 KINEMATICS OF THE EARTHQUAKE PROCESS

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C14.3D

–

213

– [197–223] 13.3.2008 12:37PM

widely used was originally proposed in 1902 by

G. Mercalli and still bears his name, although

there have been numerous modifications, with

adaptions to local building codes. It represents

the intensity of ground shaking from barely per-

ceptible to most violent, in terms of human reac-

tions, simple observations and damage to

buildings. Although the intensity scales are no

longer of interest as measures of earthquake

size, they are convenient for describing the

effects of local ground shaking and assessing

pre-instrumental events. They are used to pre-

pare isoseismal maps (contour plots of intensity)

to outline areas of greatest damage in an earth-

quake, or greatest danger from future shocks

where the variation of intensity with local

ground conditions can be assessed from geolog-

ical structure.

Structural damage is related to ground accel-

eration, although buildings respond differently

to seismic waves of different periods and are

more vulnerable to horizontal than vertical

motions. Mercalli intensity, I, is calibrated in

terms of ground acceleration, a (m s

2

), by an

approximate relationship

log

a ¼ I=3  2:5: (14:33)

The instrumental magnitude scale was

originally developed in the 1930s, for use in

California, by C. F. Richter, in collaboration with

B. Gutenberg (see Richter, 1958). Californian earth-

quakes are shallow, and consequently generate

strong surface waves, the elastic waves that are

guided by the elasticity and density contrasts at

and near the surface of the Earth. Surface waves

generally appear on seismic records with greater

amplitudes than the body waves that penetrate

the deep interior. They also have longer periods,

making their waveforms clearer on the records.

Richter magnitudes M

(a scale for local events)

was so successful that it was extended to surface

wave magnitudes, M

, applicable to more distant

(a)

30 60 120 150 240 300 360 420

2000

(b)

(c)

1500

1000

500

0.5

0 100 200 300 400 500 600

Normalized peak amplitude Distance (km)

Time (s)

FI G U R E 14.14 (a) A time sequence of fault slip for the

Sumatra–Andaman 2004 earthquake, redrawn from Ishii

et al. (2005). Light areas show active fault movement and

dark shading shows land. (b) Rupture distance along the

fault versus time. The dashed line is the straight-line

fit to the peak locations, and gives an average rupture

speed of 2.8 km s

1

. (c) Normalized peak amplitude as a

function of time, showing two significant high-frequency

energy events at 80 s and 330 s (Ishii et al., 2005).

14.6 EARTHQUAKE MAGNITUDE AND ENERGY 213

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C14.3D

–

214

– [197–223] 13.3.2008 12:37PM

earthquakes. Body-wave magnitudes, m

,arealso

used. Magnitude is defined as the logarithm of the

ratiooftheamplitudeofgroundmotion,A (in

microns), to dominant wave period, T (seconds).

With a correction term for observations at arbi-

trary distances  (degrees, subtended at the centre

of the Earth) and depth h (km), the relationship is

¼ log

ðA=TÞþf ð; hÞ; (14:34)

to which an added correction for local seismom-

eter site conditions may be needed. Amplitude

observations over a wide range of angles from

the source are needed for a reliable estimation of

magnitude because an earthquake radiates dif-

ferently at different orientations to the fault, but

recordings at several stations are needed anyway

for earthquake location so this requirement is

automatically satisfied.

It is obvious that there is a general corres-

pondence between maximum intensity, I

max

and M

, although observations of high inten-

sities in areas where ground motion is amplified

by layers of soft sediment, or focussing by geo-

logical structures, can be misleading. A rough

empirical relationship, with a term to account

for the depth h (km) of an earthquake, is

¼ 2I

max

=3 þ 1:7 log

h  1:4: (14:35)

The rapid general adoption and success of the

Richter magnitude scale is due to two features of

the definition (Eq. 14.34).

(i) The logarithmic scale permits a fine subdivi-

sion over a very wide range, with representa-

tion by a simple number that never exceeds

10. (Very small earthquakes with negative

magnitudes may be recorded locally.)

(ii) The ratio A/T is a measure of the strain ampli-

tude, E, in a seismic wave and, since the flux

of elastic wave energy passing any point is

proportional to E

, this means that magni-

tude is a measure of seismic wave energy.

The total energy depends also on the length,

or duration, of a seismic wave-train, but by inte-

grating complete seismic waveforms, a direct, if

empirical, relationship between magnitude and

energy, E (joules), is obtained:

log

E ¼ 1:5M

þ 4:8: (14:36)

Thus an increment of 1 in magnitude corres-

ponds roughly to a 30-fold increase in energy.

For some purposes it is convenient to rewrite

Eq. (14.36) in an alternative form,

E ¼ 6:3  10

expð3:45M

ÞJ: (14:37)

With the development of wide-bandwidth

seismometers, an intrinsic limitation of conven-

tionally determined magnitudes became appa-

rent. M

determinations generally use Rayleigh

waves (vertically polarized surface waves – see

Section 15.3), recorded on instruments with

periods of about 20 s. The largest earthquakes

> 8) radiate much of their energy in waves

with periods greater than this, so that the M

scale saturates and does not give sufficient dis-

crimination between very large shocks. The M

magnitude scale is based on observations of sur-

face waves with a 20 s period, and falls on dif-

ferent parts of the spectral curve for different

magnitudes (Fig. 14.13). Note that the 20 s inter-

sections with the curves have equal intervals. For

6, M

is directly proportional to the loga-

rithm of the moment, log M

, but for M

7 the

20 s period corresponds to the !

2

part of the

spectrum and so is an unsatisfactory measure

of earthquake size. Saturation of the m

scale,

which uses P-waves, compressional body waves,

often with periods of 1s but never more than 5 s,

is even more serious. As we saw in Section 14.5,

very wide bandwidth (or at least very low fre-

quency) records provide a means of estimating

, which is a better measure of earthquake size.

The relationship between seismic moment

and earthquake energy depends on the stress

release mechanism, in particular the assumption

that the final stress remaining when movement

has ceased is equal to the frictional stress across

the moving fault. The relationship is simplified by

the observation that the stress release, or stress

drop, is quite similar for virtually all earthquakes

of magnitudes exceeding about 3, as documented

for example by Kanamori and Anderson (1975).

This justifies the approach of Kanamori (1977),

who related M

to M

for shocks in the range for

which M

is not suspect and used M

as the basis of

a revised scale of magnitudes, M

.Thisiseffec-

tive for the largest shocks and coincides with M

214 KINEMATICS OF THE EARTHQUAKE PROCESS

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C14.3D

–

215

– [197–223] 13.3.2008 12:37PM

for smaller ones. As in Kanamori and Brodsky

(2004), the corresponding direct relation ship bet-

ween M

and M

(in Newton-meters) is

¼ð2=3Þlog

 6:07: (14:38)

The largest recorded seismic moment was for the

Chile, May 1960, earthquake, M

¼2.5 10

Nm,

corresponding to M

¼9.5 and an energy (com-

bining Eqs. 14.37 and 14.38) of 1.2 10

14.7 The distribution of

earthquake sizes

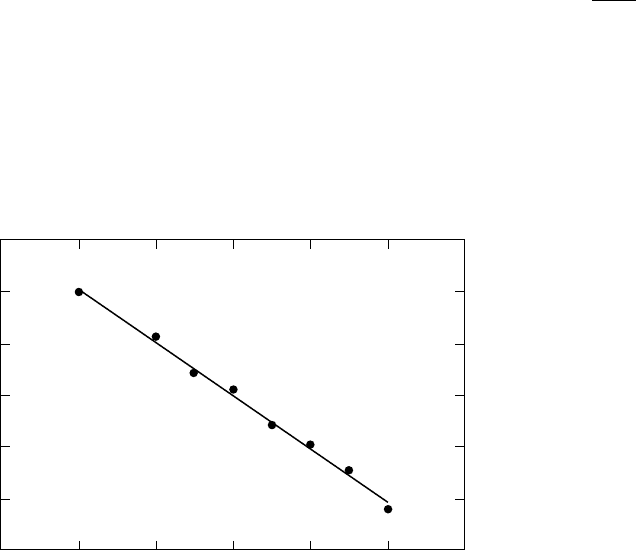
The number of earthquakes of magnitude M or

greater per year is observed to follow a simple

relationship named the Gutenberg–Richter dis-

tribution after its originators,

log

N ¼ a  bM: (14:39)

Relationships of this form, usually with b 1, are

quite generally observed in local regions as well

as globally. With numerical values of the coeffi-

cients from a global data fit by Kanamori and

Brodsky (2004), for 4 < M < 8, this is

log

N ¼ð8:0  0:2Þð1:00  0:03ÞM;

(14:40)

as plotted in Fig. 14.15. There must be limits to

the magnitude range to which this applies.

Although suggestions of a lower limit have

appeared in the literature, studies with modern

instruments, especially in deep boreholes

(Abercrombie and Leary, 1993; Abercrombie

and Brune, 1994), showed that Eq. (14.39) is

valid down to at least M ¼0. It is not clear that

there is any lower limit short of the scale of grain

boundaries in rocks. Concerning the upper limit,

Eqs. (14.39) and (14.36) together show that the

total energy release by earthquakes is exponen-

tially dependent on any assumed upper magni-

tude cut-off. Since the total energy is finite the

distribution must taper off. We consider this

problem below in terms of moments rather

than magnitudes.

First we consider the number–moment rela-

tionship corresponding to the Gutenberg–Richter

law (Eq. 14.39). Combining Eqs. (14.38) and (14.39),

we obtain

log

N ¼ log

   log

(14:41)

Nðmoment > M

Þ¼



ðM



: (14:42)

For the purpose of these equations, M

must be

understood as a dimensionless ratio, (M

/1 Nm)

and  can be interpreted as the number of earth-

quakes (per year) for which M

1 Nm. With the

numbers in Eqs. (14.38) and (14.40),  10

and

 2/3. Equation (14.42) is a power law

468357

0.1

Earthquakes/year, N

Magnitude, M

FI G U RE 14.15 Magnitude–frequency

relationship for all earthquakes for the

period 1904 to 1980. The line has a

gradient of 1, corresponding to a

b-value of 1 in Eq. (14.39). This is

effectively a log–log plot because M is

proportional to the logarithm of wave

amplitude by Eq. (14.34) or energy by

Eq. (14.36). On average, approximately

one earthquake with M 8 occurs each

year. Tapering of the distribution occurs

at magnitudes greater than 8.

14.7 THE DISTRIBUTION OF EARTHQUAKE SIZES 215

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C14.3D

–

216

– [197–223] 13.3.2008 12:37PM

distribution with fractal dimension . The essen-

tial feature of fractals is that they involve no

intrinsic scale, and over most of the observed

magnitude range earthquakes provide a classic

example. The physical processes of earthquakes

appear to be independent of size (they are ‘self-

similar’), subject to an upper limit that we now

discuss.

To calculate total moment in a given cata-

logue we differentiate (14.42) to obtain dN/dM

and then integrate M

dN (negative because

decreases with N). With the range of M

unrestricted,

0total

¼

dN ¼

M





1  

ð1Þ

: (14:43)

For <1, Eq. (14.43) is infinite. Thus, either a

maximum cut-off moment (such as the Chile

earthquake) must be assumed or the distribution

modified to give convergence of the total

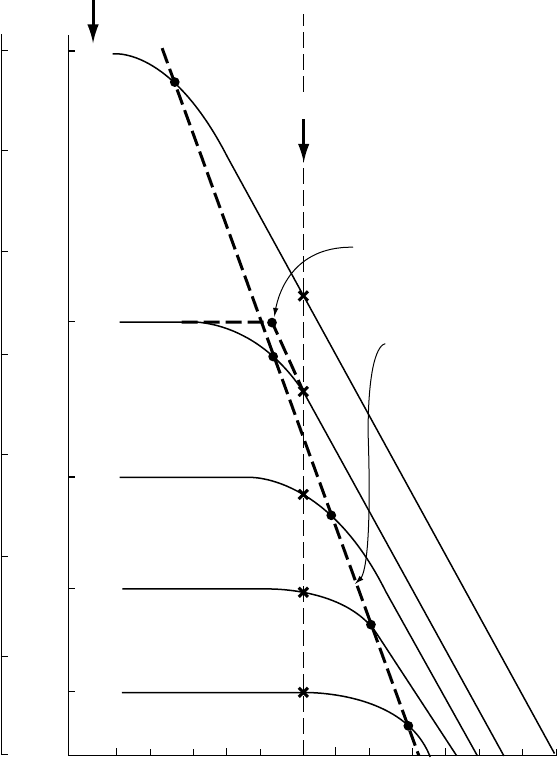
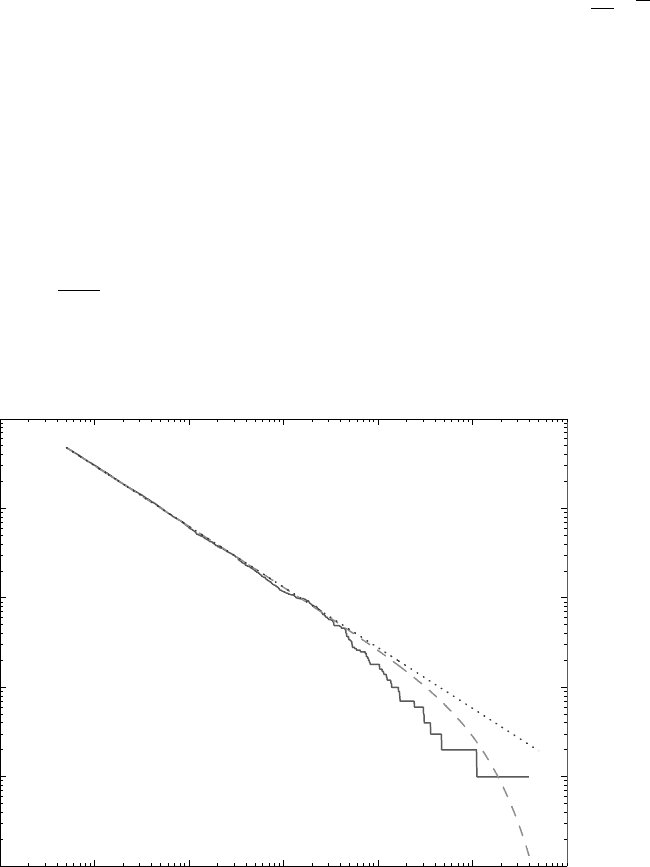
moment. Kagan (1991) modified Eq. (14.42) by

introducing an exponential term,

Nðmoment > M

Þ¼







; (14:44)

giving a roll-off in the distribution at a corner

moment M

.Thefitoftheglobaldatasetto

Eq. (14.44) is plotted in Fig. 14.16, with the assump-

tion that a common value of M

¼1.2 10

Nm is

applicable to the entire data set. Equation (14.44)

imposes a soft upper bound that can be deter-

mined from earthquake catalogues for which

statistically significant numbers of events are

available to demonstrate the taper. Bird and

Kagan (2004) found that corner magnitudes,

, corresponding to corner moments, M

, vary

between 5.9 and 9.6, depending on tectonic pro-

vince, but that  does not vary much from the

–1

Seismic moment (Nm)

Cumulative number of earthquakes

Kagan distribution

Gutenberg–Richter distribution

FI G U R E 14.16 Moment distribution for shallow earthquakes (0–70 km) from the Harvard CMT catalogue 1977–2005,

showing the evidence for a corner or taper, departing from the Gutenberg–Richter distribution at large magnitudes.

The broken line is a plot of Eq. (14.44) with M

¼1.2 10

Nm. The break in gradient at M

 4 10

corresponds to M ¼7.7. The departure from linearity at this point is significant, although statistics are uncertain in

the high moment range, with the small number of events. The single event at M

> 4 10

Nm is Sumatra 2004.

Figure provided by Yan Kagan.

216 KINEMATICS OF THE EARTHQUAKE PROCESS