Stacey F.D., Davis P.M. Physics of the Earth

Подождите немного. Документ загружается.

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C14.3D

–

197

– [197–223] 13.3.2008 12:37PM

Kinematics of the earthquake process

14.1 Preamble

Elucidation of the details of the tectonic pattern

is one of the incentives for seismicity studies.

Another is earthquake prediction. In the 1960s

and early 1970s there was a widespread, but

not universal, expectation that a decade or so

of intensive research would yield a methodology

for predicting the times, places and magnitudes

of earthquakes. The task was underestimated

because the physical mechanism of earthquakes

is not as simple as was supposed. In spite of the

lack of success we now have a somewhat clearer

perception of the earthquake process, although

rather little encouragement to believe that

detailed prediction is possible. Nevertheless,

research with this aim continues, so we can

expect further improvement in our understand-

ing of earthquake mechanisms.

The underlying driving power for earth-

quakes is derived from thermal convection of

the mantle, the subject of a thermodynamic

analysis in Chapter 22. We can compare the

energy released by earthquakes with the energy

that is shown thermodynamically to be avail-

able. Except for a few shallow shocks, for

which fault displacements are directly observed,

earthquake energies are estimated from the radi-

ated elastic waves. Energy is directly related to

magnitude and, given the numbers of earth-

quakes as a function of magnitude, we can inte-

grate over all earthquakes to estimate the total

energy release. Typically, the efficiency for con-

version of static elastic energy to seismic waves

is estimated as 6%. Although there is substantial

uncertainty in this number, it suffices for an

order of magnitude estimate of the fraction of

total convective energy that is released as earth-

quakes, 3%. Most of the mantle deformation

occurs aseismically. Implications for rheology

and the pattern of mantle convection are consid-

ered in Sections 12.5 and 13.2.

Most earthquakes occur at depths too great to

allow access to the source zones with boreholes

or tunnelling. The earthquake process is gener-

ally inferred from radiated seismic waves, but

direct observation of surface displacements in

some shallow shocks give convincing confirma-

tion of the mechanism. To a first approximation

an earthquake is a dislocation (Fig. 10.5), with

displacement of the rock on opposite sides of a

fault that grows from a starting point, termed

the hypocentre. The spectrum of radiated waves

is characteristic of fault dimensions and can be

used to estimate them. The lowest frequencies,

(longest wavelengths) are used to estimate earth-

quake strength or moment. Seismic moment is

the product of slip, area of a fault and elastic

modulus. Detailed seismic analysis of waves

from very large earthquakes, such as the 2004

Sumatra–Andaman event, reveals that, at any

instant, movement is restricted to a limited

area of the fault, a slipping patch, that travels

from one end of the fault to the other, breaking

material in front of it and leaving behind broken

material that eventually ‘heals’. Waves ‘pile up’

in the forward direction and are spread out in

the backward direction. This directivity, appa-

rent as an asymmetry in the radiation pattern,

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C14.3D

–

198

– [197–223] 13.3.2008 12:37PM

is a Doppler effect, and is used to determine the

direction and speed of fault propagation. Modern

seismic arrays reveal fine details, indicating that

large dislocations can be regarded as superposi-

tions of many sub-events.

Plate tectonic reconstructions and space

geodesy have been used to calculate slip across

tectonic boundaries. Comparison with the slip

evident in earthquakes allows an estimate of

the fraction of the plate motion in a given

tectonic region that is accounted for by earth-

quakes and not by aseismic creep. Because very

large earthquakes are rare, summing moments

from historic earthquakes is inadequate. Most of

the slip takes place in the largest events.

Section 14.7 describes a method of estimating

the effects of the rare large events by a statistical

analysis of the smaller events.

Large thrust and normal earthquakes in the

sea floor cause vertical motions that generate

tsunamis. Only earthquakes with fault dimen-

sions hundreds of kilometres in extent are effec-

tive. They cause tsunamis, with wavelengths

comparable to the fault dimensions, that propa-

gate in oceans, 5 km deep, as shallow water

waves, meaning that they have wavelengths

much greater than the water depth. The waves

travel across the ocean at a speed more than an

order of magnitude faster than normal wind

driven waves but less than the speeds of seismic

waves by a similar factor. Seismic signals are

used as a basis of tsunami warning systems, sup-

plemented by sea floor pressure observations.

14.2 Earthquakes as dislocations

Earthquakes result from rapid fault slip but only

rarely do the faults break the surface. Shallow

transcurrent (strike-slip) faults, across which

horizontal displacements occur at the surface,

provide an exception. The San Andreas fault

in California is a notable example. Thus, the

seismicity of California has played a vital role

in recognizing earthquakes as fault movements.

An example is shown in Fig. 14.1. The fact that

repeated movements occur in the same direc-

tion, and accumulate as large fault offsets, is

illustrated in Fig. 14.2, making it obvious that

earthquakes are local increments in the pattern

of tectonic motion.

Impressive as horizontal movements on trans-

current faults often are, it is important to recog-

nize that they have a secondary role in the

tectonic scheme. The energy is ultimately deri-

ved from convection, for which the essential,

primary mass movements are vertical. The

world’s major thrust faults (see Fig. 14.10(b)),

FIGURE 14.1 Fault

displacement that occurred

though an orange grove during

an earthquake in Imperial Valley,

California, in September, 1950.

Photograph by David Scherman,

Life Magazine # Time Inc.

198 KINEMATICS OF THE EARTHQUAKE PROCESS

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C14.3D

–

199

– [197–223] 13.3.2008 12:37PM

across which vertical slip occurs, are responsible

for most of the moderate and large earthquakes,

but they are generally deeper and are not directly

observed. Decades of observations of fault move-

ments so strongly emphasized horizontal dis-

placements that they probably delayed by many

years recognition of the underlying tectonic

mechanism.

The San Francisco earthquake of 1906 has a

special place in the history of seismicity studies.

A geodetic survey of the area had been com-

pleted shortly before the earthquake and was

repeated after it, providing detailed, quantitative

documentation of the displacements. Reid (1910)

used the data to support what he called the elas-

tic rebound theory of earthquakes. The theory

was not entirely new, but Reid’s evidence made

it convincing and it became central to ideas

about the earthquake mechanism. The elastic

rebound theory is represented diagrammatically

in Fig. 14.3. It envisages a progressive regional

movement, causing elastic deformation of the

ground until a breaking point is reached, when

displacement across a fault releases the elastic

strain. The concept of a progressive regional

movement causing build-up of elastic strain,

which is abruptly released in occasional events,

falls naturally into place with current ideas

about plate tectonics. Thus the essential validity

of the elastic rebound theory is not subject to

doubt. However, the concept of a breaking point

is simplistic. We still have no clear idea of what

FIGURE 14.2 Mismatch of

geological features across a

branch of the San Andreas fault

near Indio, California. Photograph

by Spence Air Photos.

(a)

(b)

FIGURE 14.3 The elastic rebound theory of an

earthquake, as advanced by Reid (1910) to explain the

San Francisco 1906 event. Regional shearing movement

gradually builds up elastic strain from state (a) to state

(c), at which it is suddenly released across the fault,

producing the displacement in (d).

14.2 EARTHQUAKES AS DISLOCATIONS 199

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C14.3D

–

200

– [197–223] 13.3.2008 12:37PM

triggers earthquakes or what limits the spread

of a fault break once it starts. This is a difficulty

that limits progress in earthquake prediction.

Fault displacements, and the associated elas-

tic strains and stresses, are described by equa-

tions that are collectively termed dislocation

theory. Some of the jargon is adopted directly

from solid-state physics in which there is an

extensive literature on dislocations. They occur

as defects in crystals and control their strengths

and mechanisms of deformation. There are two

basic kinds, illustrated in Fig. 10.5. Consider a

solid body of convenient shape, make a half-cut

in it and displace the material on opposite faces

of the cut. The axis of the dislocation is the edge

of the cut and the relative displacement of the

faces is the displacement or Burgers vector. If this

is parallel to the axis, as in Fig. 10.5(a), then the

result is a screw dislocation. If the displacement

vector is perpendicular to the axis (Fig. 10.5(b)),

it produces an edge dislocation, and in general

we have mixed dislocations, with both types of

displacement.

To a useful approximation, the San Francisco

1906 earthquake can be modelled as a screw dis-

location. Another intensively studied earthquake,

Alaska 1964, resembles a pair of edge disloca-

tions. These simple models represent faults that

are much longer in one dimension than the other.

The simple dislocations envisaged in Fig. 10.5 are

described by two-dimensional equations, that is,

they assume uniformity along the axis or an effec-

tively infinite length. More general equations

are needed for faults that are nearer to equi-

dimensional (see Section 14.3). Another generali-

zation that is needed for realistic application to

earthquakes is a grading of slip to zero at fault

boundaries. For faults that break the surface it is

the gradient of the slip that must be zero at the

surface.

Ground displacements accompanying the San

Francisco 1906 earthquake extended for hund-

reds of kilometres along the San Andreas fault,

but were concentrated in a band about 15 km

either side of it. This means that the break was

shallow and quite well represented by a screw

dislocation, although the slip was variable along

the length of the fault. Figure 14.4(a) gives the

geometry for a simple screw dislocation that

models this situation, with its axis parallel to the

surface at depth D. Initially we calculate the strain

for a dislocation in an infinite medium and then

take account of the free surface by introducing

a hypothetical image dislocation above the sur-

face. For the infinite medium the circle of radius r

about the dislocation axis, which is shown as a

(b)

Fault

displacement

(a)

Surface

fault

Dislocation axis

FIGURE 14.4 (a) Geometry of a screw dislocation, the mathematical model of a transcurrent fault. Displacement, S,

is uniform to depth D and zero below that, twisting the circle (broken line) into a helical form. (b) A more realistic

variation of displacement with depth.

200 KINEMATICS OF THE EARTHQUAKE PROCESS

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C14.3D

–

201

– [197–223] 13.3.2008 12:37PM

broken line for the unfaulted medium, is defor-

med to the helical curve (solid line). The shear

strain, ", is uniform around the circumference

of this circle and is therefore given by

" ¼ b=2pr; (14:1)

where b is the displacement (Burger’s vector). We

are primarily interested in the component "

this strain across a vertical plane, y ¼constant,

parallel to the fault plane (y ¼0),

2pr

ðx

þ y

2Þ

: (14:2)

This gives the strain component in an infinite

medium, due to a single dislocation of displace-

ment, S ¼b.

We may now consider the effect of a free sur-

face at x ¼D. Since there are no stresses across

the surface, the shear strain across it, "

, is zero

everywhere on the plane. Mathematically, this

situation can be achieved by introducing to the

infinite medium a hypothetical mirror image

dislocation at x ¼2D. The effect of the two dis-

locations together would be to give slip S for

0 < x < 2D but zero outside this range. The second

dislocation does not cancel "

, which becomes

2pr

þ y

2D  x

ð2D  xÞ

þ y

: (14:3)

In the free surface (x ¼D), where observations are

normally made,

¼ "

ðDÞ¼

pðD

þ y

: (14:4)

Thus displacements of surface points at arbi-

trary distance, y, from the fault are obtained by

integrating the strain, "

, with respect to y, not-

ing the discontinuity in displacement at y ¼0,

displacement ¼

1

dy ¼

1 

tan

1



: (14:5)

Equation (14.5) gives the surface displace-

ment (in the z direction) due to a simple disloca-

tion with a discontinuity of fault displacement

on the dislocation axis at depth D (x ¼0). There

are singularities in stress and strain on the

axis and the model can be improved by grad-

ing the fault slip to zero as x !0(butkeeping

the variation of slip with depth zero as x !D)

as in Fig. 14. 4(b). The effect of these refine-

ments is too slight to affect the f it of the

geodetic observa tions (Fig. 14.5) made after

the 190 6 earthquake, and the curve shown is

for a simple dislocatio n. Other unmodelled

effects include variabili ty of displac ement

along the fault and heterogeneity of the

medium. Recent ly mu ch finer o bserv ations

using radar interferometry from satellite s

have provided detailed displacement maps

that allow heterogeneity to be identified

(Peltzer et al., 1999). A cross-section of ground

displacements resu lting from the 1996 Manyi

810

Displacement (metres)

Distance from fault (kilometres) NE

FIGURE 14.5 Horizontal

displacement of surface points on

the NE side of the San Andreas

fault that occurred during the San

Francisco 1906 earthquake. The

curve represents Eq. (14.5) with

S ¼4 m and D ¼3.4 km. To allow

for grading of slip, as in Fig.

14.4(b) a somewhat greater total

fault depth must be favoured.

14.2 EARTHQUAKES AS DISLOCATIONS 201

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C14.3D

–

202

– [197–223] 13.3.2008 12:37PM

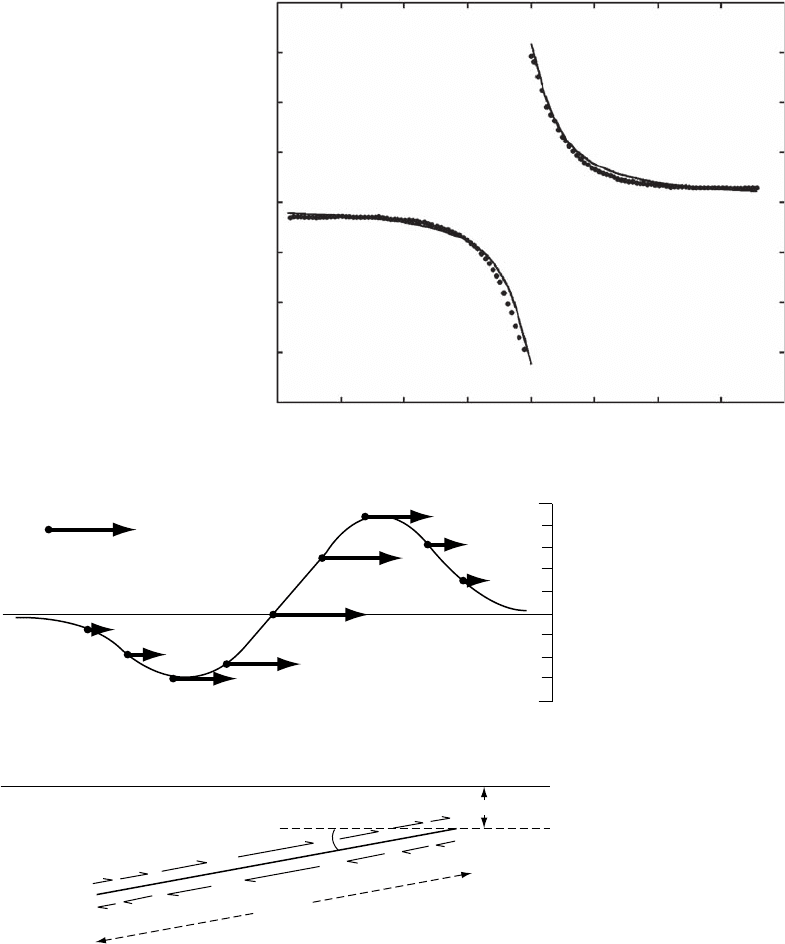
strike-slip earthquake in Tibet (Fig. 14.6 ) show

a r emarkable fit to predictions of Eq. (14.5 ),

but asymmetry of other cross-sections led

Peltzer et al. to conclude that elast ic response

about the fault was variable.

A model of the Alaska 1964 earthquake is

shown as the lower part of Fig. 14.7, with corre-

sponding surface displacements, in the top half

of the figure, matched to the available observa-

tions. The Alaska 1964 earthquake cannot be

–400

–300

–200

–100

100

200

300

400

–80 –60 –40 –20 0 20 40 60

Displacement (cm)

Distance perpendicular to fault (km)

Manyi (Tibet) Mw 7.6 earthquake

FIGURE 14.6 Displacements

determined from InSar

(interferometric synthetic

aperture radar) for the 1996

Manyi, Tibet, earthquake, from

data by Peltzer et al. (1999). A fit to

Eq. (14.5), with S ¼6.84 m, and

D ¼7.9 km, of data provided by

Gilles Peltzer.

–4

Vertical displacement (m)

Horizontal

displacement vectors

Sea level

(20

250

–22

+22

FIGURE 14.7 A model of fault movement during the Alaska 1964 earthquake, matched to observed displacements

of the surface reported by Plafker (1965). The model assumes that the fault did not break the surface, but if it did so

the break would have been at sea.

202 KINEMATICS OF THE EARTHQUAKE PROCESS

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C14.3D

–

203

– [197–223] 13.3.2008 12:37PM

modelled as simply as the San Francisco 1906

earthquake. It is represented by a pair of com-

pound edge dislocations with graded displace-

ments. This is a two-dimensional model. The

fault length, roughly parallel to the Alaska

coast, was about 800 km, four times the width

and sufficient to make the two-dimensional

model satisfactory over the central section of

the fault. Equations for edge dislocations, not

presented here, are not as simple as those for

screw dislocations, partly because the free sur-

face cannot be accounted for by a single, simple

image. Equations for displacements due to arbi-

trarily oriented faults are given by Mansinha and

Smylie (1971) and Okada (1985).

We can estimate the maximum strains, close

to the faults, for the two earthquakes consid-

ered and use the elasticity of the Earth at app-

ropriate depths to obtain the corresponding

stresses. For San Francisco we may take the

movement on each side of the fault to be 2 m

and distribute this displacement over the depth

of the fault. The simple dislocatio n model gives

the depth as about 3.5 km, b ut a deta iled analy-

sis, using a more realistic c ompound dislocation

model, gives (5.0 1.5) km. It is puzzling that

the movement on a fault break hundreds of

kilometres in length should be so shallow, but

using the latter figure, the strain is 4 10

4

and

taking the crustal rigidity as 30 GPa the drop in

shear stress across the fault was 1 2 MPa (120

bar). This is an u pper bound, as slip was variable

along the fault and a high value is assumed.

On other fault sections the stress drop may not

have exceeded 2 MPa. For the Alaska 1964 shock

we distribute the 22 m maximum displacement

over the half-width of the fault, 125 km, to

obtain a strain of 1.8 10

4

. At t he greater

average depth of this shock the shear modulus

is about 55 GPa, giving a stress drop of 9.9 MPa

(99 bar). Acknowledg ing the unce rtaint ies in

these calculations, we can guess that a stress

drop of order 10 MPa (100 bar) is typic al of

large, shallow shocks. Estimates in the range 1

to 10 MPa are derived from studies of the spectra

of seismic waves (Section 14.5). These stresses

are m uch less than the breaking stress of pre-

viously unfractured rock. Most earthquakes fol-

low lines of pre-existing weakness.

14.3 Generalized seismic moment

Even for earthquakes on faults that break the

surface, the pattern of surface displacements

is normally very irregular and incompletely

recorded and there are no direct measurements

of displacement at depth. Moreover, we are inter-

ested in the sequence of events during an earth-

quake, including details such as the point of

initiation (hypocentre) and the speed of fault

propagation. To obtain this information we

must decipher the records of the radiated elastic

waves. For many years earthquakes have been

locatedbytimingwavearrivalsatwidelydistri-

buted observatories and Chapter 17 discusses the

use of seismic wave arrival times to infer the

Earth’s internal structure. This chapter is concer-

ned with the information that can be obtained

about earthquakes themselves. Although they are

complicated phenomena and are certainly not all

the same, some clear patterns have emerged.

The screw and edge dislocations discussed

in the previous section are simplified two-

dimensional models of earthquake sources. In

three dimensions, dislocation patches are used,

as developed in this section. The measure of

earthquake strength is seismic moment, which

takes into account the elasticity of the medium,

the amount of displacement, and the area over

which the displacement occurs. The scalar seis-

mic moment M

is given by

bdS; (14:6)

where  is rigidity modulus of the faulted

medium and b is the distribution of slip across

a fault of area S. In three dimensions seismic

moment becomes a tensor, considered below.

Calculation of the radiation field from

an earthquake fault is a complicated mixed-

boundary problem, in which stress (friction) and

displacement conditions must be simultaneously

satisfied on both faces of the fault. The problem

is simplified by replacing the fault by combina-

tions of point forces in a continuous elastic

medium that can be adjusted to be equivalent

to motions across a discontinuous surface. Such

point forces have relatively simple analytical

14.3 GENERALIZED SEISMIC MOMENT 203

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C14.3D

–

204

– [197–223] 13.3.2008 12:37PM

solutions and so can be superimposed to repre-

sent any internal dislocation of the medium.

A point force in an infinite medium can be

thought of as a force that is exerted at a point, a

finger that is inserted and pushes in a particular

direction. The elastic material resists this push

and the material moves until the elastic restor-

ing force balances the disturbance. The material

is compressed in front of the force and expands

behind it. The force may be dynamic, i.e. varying

in time, or static.

For a point force, F

, applied at the origin, the

equilibrium equations (Eq. 11.43 ) become

@

þ F



¼ 0; (14:7)

where repeated indices are summed. The solu-

tion to this equation is the Green’s function

(Landau and Lifshitz, 1975),

4p





4ð1  Þ



; (14:8)

where G

is the displacement in the i-direction

from a unit point force in the k-direction. The

point force on its own has limited application in

geophysics. A special case of a point force applied

to the surface of an elastic half space, the so-

called Boussinesq problem, is used in modelling

surface loads. One example is the load imposed

on the surface by an impounded lake. Gough and

Gough (1970) used a distribution of half-space

point forces to describe the displacements and

stresses associated with the filling of Lake Kariba

in Zimbabwe. Comparison with the induced seis-

micity and deformation measured by levelling

confirmed that elastic constants determined for

the upper crust from seismology also describe

static loading.

By differentiating Eq. (14.8) we obtain equa-

tions describing dislocations in three dimensions

that are much more general than the equations

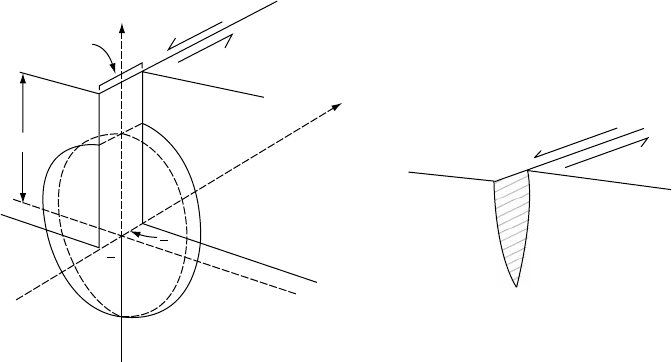
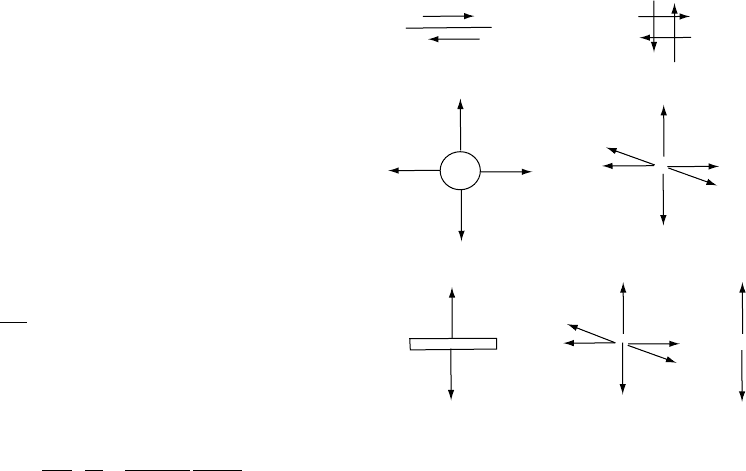
of the previous section (Eshelby, 1973). Opening

of a dike or tension crack is modelled by a third

type of dislocation in which the Burgers (displace-

ment) vector is normal to the crack surface. A

cavity inflation is modelled in the far field, by

three surfaces at right angles with displacement

normal to each, whereas a collapse corresponds

to displacement in the opposite sense. Each of

these cases can be modelled by combinations of

derivatives of the point force equations (Fig. 14.8).

For each case of dislocation sliding, opening

or volume collapse, the force combination must

have no net force and no net moment, because

the end result has neither linear nor rotational

acceleration. For an earthquake dislocation

model, slip is tangential to the fault plane and

in opposite directions on opposite sides. We

model the slip on the two sides in terms of oppo-

sitely directed point forces, which together form

a couple. However, a couple has a net torque, so

its sudden appearance at the time of an earth-

quake would develop an accelerating angular

momentum. To avoid this, a second couple

must be added with an equal and opposite torque

and forces at right angles to the first. The result is

the double-couple model of earthquakes.

To form the individual couples we use the

same mathematical procedure as in electro-

statics to form a dipole. Suppose that the two

surfaces of the displaced crack are a distance z

apart, which in the limit we will decrease to zero.

Let the normal to the crack area, S, be parallel to

the z-axis, and the horizontal displacement, b,in

the x-direction. The strain is b/z. Then the force

is (b/z)S. The displacement generated by the

upper and lower forces is

Fault Double couple

Pressurized sphere Center of dilatation

Opening crack Centre of dilatation + Force doublet

FIGURE 14.8 Point force representations of elementary

dislocations.

204 KINEMATICS OF THE EARTHQUAKE PROCESS

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C14.3D

–

205

– [197–223] 13.3.2008 12:37PM

ðcoupleÞ¼force G

r þ

z



 G

r 

z



bS

z

r þ

z



 G

r 

z



¼ bS

; ð14:9Þ

where bS is seismic moment (Eq. 14.6), and G

is the Green’s function as in Eq. (14.8). Adding a

compensating couple at right angles, of the same

strength but opposite torque, we have

ðdouble couple Þ¼bS



: (14:10)

Here the force couple is made up of two equal

and opposite forces displaced normal to their

line of action. Seismologists use a similar con-

struction to model the opening of a crack. The

forces in this case are displaced in the direction of

opening or parallel to their line of action to form

a force doublet. Three doublets added together

at right angles make a centre of dilatation.

ðcentre of dilatationÞ¼lbS



(14:11)

A centre of dilatation is used to model a

spherical region that expands. Combinations

of unequal doublets can be used to model the

expansion of ellipsoidal regions (Davis, 1986). A

much-used application of the centre of dilata-

tion solution is the Mogi model of stressing of a

volcano by a magma chamber (Anderson, 1936;

Mogi, 1958). However, in that case extra image

terms are added to the equations to cancel trac-

tions on the surface of the Earth.

Opening of a crack is modelled by combining

a centre of dilatation and a doublet oriented in

the direction of opening. The full expression is

ðtension crackÞ¼bS l



þ2



; ð 14:12 Þ

where l is the Lam

e parameter (see Section 10.2).

In general b varies over the dislocation surface

and to model finite faults the solutions are int-

egrated and may include time variation, as in

Sectio n 14.5.

Equations (14.10) to (14.12) may be general-

ized to incorporate both shear and dilatation,

¼ M

; (14:13)

where M

is the seismic moment tensor, defined

in connection with Eq. (14.6), and given by

¼ l

þ ðb

þ b

Þ; (14:14)

where b and S are components of the vectors

b and S and

is the displacement in the

i-direction from a point force in the p-direction,

differentiated in the q-direction to form a couple

or doublet.

Equation (14.13) gives the displacement in

the i-direction for an average Burgers vector,

b, dislocating a surface, S, in terms of derivatives

of the equations for displacements by elemen-

tary point forces, that is, in terms of couples and

doublets. The shear crack lying in the x–y (1–2)

plane has a moment tensor given by

00b

000

b

S 00

; (14: 15)

and the tension crack in the y–z (2–3) plane,

ðl þ 2Þb

S 00

0 lb

S 0

00lb

: (14:16)

Equation (14.15) demonstrates a fundamental

non-uniqueness in inverting measured displace-

ments to determine which plane has slipped

in an earthquake. Suppose that we invert

Eq. (14.13) to determine M

and obtain values

corresponding to Eq. (14.15). Because of the sym-

metry of the tensor we cannot distinguish

between slip on the z plane in the x direction

and slip on the x plane in the z direction, with

¼M

. If slip occurs on the x-plane then the

z-plane is referred to as the auxiliary plane. This

is a consequence of using the point represen-

tation of an earthquake, as reconsidered in the

following section. If we invert displacement data

from a finite source we can obtain the extent and

orientation of the fault plane, i.e. M

(x,y,z)

as discussed in Section 14.5. The generalized

moment tensor of an earthquake is obtained

14.3 GENERALIZED SEISMIC MOMENT 205

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C14.3D

–

206

– [197–223] 13.3.2008 12:37PM

by inverting Eq. (14.13) where the dynamic

Green’s function (Aki and Richards, 2002) is

used. One can rotate the tensor, as we did for

stress in Chapter 11, to obtain the fault plane

and the auxiliary plane. The moment can then

be represented as a fault plane solution for

which the plane and the slip across it are speci-

fied. For a shear dislocation, such as an earth-

quake, the trace of the moment tensor is zero,

that is, there are no opening or closing sources

(cracks).

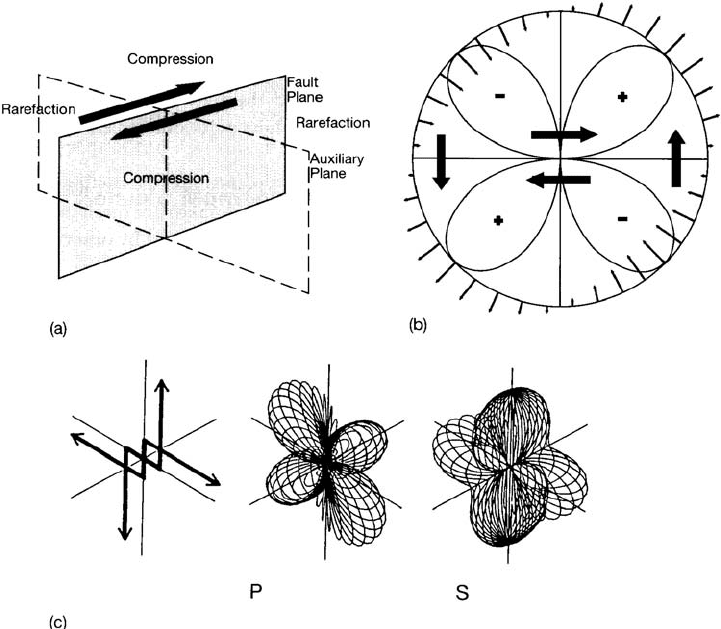
14.4 First motion studies

The direction of the initial movement in a seis-

mic wave, at an observing station remote from

an earthquake, depends in a systematic way

on the orientation of the fault and direction of

slip relative to the station. In an infinite, uni-

form medium the pattern of compressional

(P-wave) first motions would be simple. The

medium would be divisible into four quadrants,

with one opposite pair experiencing initial

compression (motion away from the source)

and the other pair initial dilation (motion

towards the source). If we consider the double

couple the heads of the force arrows will form

compressions and the tails extensions. The

boundaries of the quadrants are the fault

plane and the auxiliary plane perpendicular to

it, as in Fig. 14.9(a). The radiation pattern is

shown in Fig. 14.9(b), as viewed in a plane per-

pendicular to both the nodal (fault and auxiliary)

FIGURE 14.9 (a) Separation of compressions and rarefactions of the first motions of seismic P waves by the fault

plane and an auxiliary plane perpendicular to it. (b) P-wave radiation pattern viewed in a plane perpendicular to

the fault and auxiliary planes. At angle  to this plane the amplitude is reduced by the factor cos . (c) A three-

dimensional view of the radiation pattern from a double couple point source with the orientation shown (from

Kennett, 1983, p. 90).

206 KINEMATICS OF THE EARTHQUAKE PROCESS