Stacey F.D., Davis P.M. Physics of the Earth

Подождите немного. Документ загружается.

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C15.3D

–

237

– [224–238] 13.3.2008 12:00PM

Thus the block model gives 

¼ 2.5% for all

magnitudes. The low radiation efficiency is a

consequence of the limited accelerations permit-

ted by dynamical modelling of the motion of the

sliding block. Kinematic models with assumed

displacement-time histories that give higher

accelerations allow much higher efficiencies.

For example, Singh and Ordaz (1994) found that

the Brune model (Eq. (14.32)) gives 

¼46% and

that if the model is modified to give a sharp

corner frequency, 

¼86%. Ide et al. (2003) obtain

a well-constrained value of 66% from borehole

data.

There are a number of reasons why obser-

ved radiation efficiencies (Venkatamaran and

Kanamori, 2004; Kanamori and Brodsky, 2004)

are much higher than for the smooth sliding

block model. Models of dynamically spreading

cracks (Madariaga, 1976; Das, 1981) show that

healing waves are generated at boundaries

where the cracks stop. The healing waves

quench the motion in the interior of the crack

significantly earlier than friction alone. Another

reason is the dependence of the coherence of

high-frequency radiation on the spacing of

near-field network stations. For coherence, the

wavelength of the radiation must be longer than

the station spacing (Dainty, 1995). This means

that at shorter wavelengths the stations are

receiving signals from different patches of fault

and therefore the high frequency radiation is not

generated by smooth motion of an extended

fault, but by semi-independent motion of small

patches. This can be attributed to variable fric-

tion and high local accelerations, with heteroge-

neous fracturing adjacent to the fault. This leads

to an erratic moment–time history with a larger

value of

dt in Eq. (15.47).

If earthquakes have a seismic efficiency of 6%,

as McGarr (1999) suggests, the question arises

that why, if the remaining 94% of the energy is

taken up as frictional heat, a heat flow anomaly

is not observed on large strike-slip faults such as

the San Andreas (Lachenbruch and Sass, 1980).

The absence of a heat flow anomaly has promp-

ted several speculations. The possibility that

dynamic fault friction somehow becomes low

has been considered, but this is difficult to

reconcile with the high deviatoric stresses

measured in boreholes (McGarr, 1999). Some

energy is consumed in breaking rock and pow-

dering it to produce fault gouge (see recent dis-

cussion by Abercrombie and Rice, 2005), but we

find this to be inadequate, and a more plausible

alternative is the flow of ground water as the

principal mechanism for the removal of locally

generated heat. A significant fraction of rainfall

on land sinks in to become ground water. It

cannot accumulate in the long term and flows

to the sea by whatever channels are easiest, and

fault zones are broken up and porous, making

them easy paths. Flow of ground water extends

much deeper than is often recognized, as empha-

sized by a comment on discoveries from the deep

(KTB) borehole in Germany (Haak and Jones,

1997): ‘Another major surprise was the presence

of abundant fluids ... throughout the complete

depth range ... with the astonishing result that

the formation pressure remains hydrostatic

down to the base of the hole at 9100 m.’

15.7 Foreshocks and prediction

ideas

The average interval between major earthquakes

on sections of fault where they occur is typically

100 years or more. Thus, if we take the magni-

tude of the elastic strain release to be 2  10

4

the average rate of its build-up between shocks is

no more than 2  10

4

/100 years ¼ 6  10

14

1

We may compare this with the rate of change of

tidal strain in the solid Earth. The strain ampli-

tude of the lunar tide is about 5 10

8

, cycled in

12.4 hours and giving a maximum strain rate of

ð2  p  5  10

8

=12:4Þhour

1

¼7  10

12

1

This is 100 times the average rate of seismic

strain build-up. But earthquake occurrences are

not related to the tidal cycle. Therefore the con-

cept of a sharply defined breaking stress appears

irrelevant and the system is governed by time

delays to instability (Eq. (15.18)).

The energy released during an earthquake is

stored as elastic strain energy in the focal region

immediately before the shock. Early efforts to

find an earthquake prediction method were

based on the supposition that this energy

15.7 FORESHOCKS AND PREDICTION IDEAS 237

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C15.3D

–

238

– [224–238] 13.3.2008 12:00PM

would be recognizable from measurements of

stress, strain or related secondary effects. But,

as noted in the preceding sections, seismic stress

release does not normally exceed about 10 MPa

(100 bar); this is less than the static stresses

that are often found in seismically stable areas,

so the expectation was rather that seismic

stresses or strains would display a characteristic

time-dependence, indicative of instability. In

Section 15.3 we present a model of earthquake

initiation, which depends on the instability

of small patches that are probably too small to

observe by prediction techniques currently under

investigation. As suggested in Section 15.1, the

hope may be in recognition of what we refer to

as vulnerability rather than instability. If a given

patch is to trigger others and grow into a large

earthquake, it requires a general elevated vulner-

ability. Stress levels over a wide area would need

to be high, approaching the failure stress. This

has been termed critical instability, and it has

been suggested that it may be detectable in a

regional sense as long-range correlations of pre-

event seismicity (Keilis-Borok, 2002), with accel-

erating foreshock moment release as critical

patches are activated (Bowman and King, 2001).

Reasenberg (1999) notes that short-term earth-

quake clustering is the strongest non-random

feature observed in earthquake catalogues.

It allows one to obtain short-term probabilis-

tic forecasts of future earthquake activity. No

other phenomenon currently provides such a

possibility. However, in that most large earth-

quakes are not preceded by identifiable fore-

shocks, they are, at present, unpredictable.

The Epidemic Type Earthquake Sequence

(ETES) model, developed by Kagan and Knopoff

(1987) and Ogata (1988), is based on the

Gutenberg–Richter or Kagan laws (Section 14.7)

to model the magnitude distribution, and

Omori’s law to characterize the decay of triggered

seismicity after any shock. The model assumes

that each earthquake may be simultaneously a

mainshock, aftershock and/or foreshock. Up to a

limit imposed by the corner magnitude of the

frequency distribution represented by Eq. (14.44),

each earthquake of magnitude M triggers after-

shocks with a rate proportional to 10

M

,which

decays with time according to Omori’s law,

1=ðt þ cÞ

(Eq. (15.27)). Thus each earthquake has

a finite probability of triggering a larger one. The

model gives the probability of triggered events as

a function of space and time by superimposing

the triggering probabilities of all preceding

earthquakes.

The spatio-temporal distribution of triggered

events at distance r and at time t after an earth-

quake of magnitude M is



ðr; tÞ¼K  10

M

wðtÞf ðr; MÞ; (15:53)

where K is a constant,  is the productivity of

aftershocks from an event of magnitude M. wðtÞis

a normalized version of Omori’s law,

wðtÞ¼

ðt þ cÞ

; (15:54)

and f(r,M) is a normalized distribution of horizon-

tal distance between events. For example, Kagan

and Jackson (2000) use functions of the form

f ðr; MÞ¼



exp½r

=ð2

Þ; (15:55)

where 

is the scaling parameter (standard devi-

ation) and increases with M. Equation (15.53) is

fitted to historical catalogues, using statistical

methods. The cumulative sum of probabilities

has been used to construct probability maps

against which future activity can be tested. They

show clustering, of which the most obvious man-

ifestation is aftershock sequences. The model,

applied to catalogues from which recognized

aftershock sequences have been removed, also

identifies clustering (Kagan and Jackson, 1994),

albeit weaker than for aftershocks. Major shocks

around the Pacific rim are positively correlated in

adjacent regions rather than occurring in seismic

gaps, which was the earlier expectation.

238 EARTHQUAKE DYNAMICS

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D

–

239

– [239–266] 13.3.2008 11:41AM

Seismic wave propaga tion

16.1 Preamble

The consideration of elastic waves in this chapter

is a preliminary to their use in Chapter 17 to study

the internal structure of the Earth, but also an

extension to the discussion of elasticity in

Chapter 10. Virtually all the information that we

have on the elasticity of the Earth is obtained

from observations of seismic waves. Tidal defor-

mation (Section 8.2) and the period of the

Chandler wobble (Section 7.3) give supplemen-

tary data that extend to low frequencies, but

lack the detail and precision of seismology. In

the full context of the subject, seismological

observations can be considered to extend to zero

frequency if the static strains of earthquake dis-

placements are included, but the lower limit of

seismic wave frequencies is 3 10

4

Hz, the 54

minute period of the

mode of free oscillation.

At the other end of the scale, waves with frequen-

cies of order 1 Hz are recorded at observatories

remote from the earthquakes that generate them;

for more local studies, and especially in explora-

tion seismology, much higher frequencies are

used. With this wide frequency range it is neces-

sary to recognize a slight frequency dependence

of elasticity and consequent dispersion of elastic

waves (Section 10.7). Without an allowance for

this there is a small, but noticeable, discrepancy

between models of the Earth derived from high-

frequency body waves (Section 16.2) and free

oscillations (Section 16.6).

We recognize also a contribution to frequency

dependence that arises from heterogeneity.

Variations in elastic properties on a scale that is

small compared with the wavelengths of seismic

waves are averaged in the manner of the unre-

laxed modulus considered in Section 10.4.

Wavelengths that are shorter than the scale of

heterogeneities introduce a local refraction/dif-

fraction problem. A patch of low velocity mate-

rial delays waves passing through it and may lose

its effect if the faster waves in the surrounding

medium diffract around it, causing the wave-

fronts to ‘heal’ and obscure the existence of the

patch. Conversely, waves passing through a high

velocity patch will be refracted so that they

spread out, making the patch appear larger to

an observer on the far side (Section 16.3). The

effect is to bias the wave speed to a higher value

than seen by longer waves that take a gross aver-

age of the elasticity. This was drawn to attention

by Wielandt (1987) and is the subject of a

detailed analysis for the case of random hetero-

geneities (Roth et al., 1993). It gives a frequency

dependence to seismic velocities additional to

that arising from anelasticity and considered in

Section 10.7.

It is convenient to distinguish three types of

wave, body waves, surface waves and free oscil-

lations, although there is no sharp distinction

between them. High-frequency body waves

(Sections 16.2–16.4) have wavelengths that are

short compared with the curvature of the Earth

and their propagation has a close analogy in the

propagation of light waves in an optical system.

The analogy leads to the concept of seismic rays,

the normals to the wave fronts. These are

refracted and reflected in the same way as light

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D

–

240

– [239–266] 13.3.2008 11:41AM

rays, but one difference must be noted. There is

no optical equivalent to the compressional (P)

waves, but only to the transverse (S) waves of

seismology. As we consider waves of lower and

lower frequencies, with correspondingly longer

wavelengths, the body wave ray theory becomes

less appropriate. For wavelengths that are signi-

ficant fractions of the radius of the Earth we

must consider instead the normal modes of the

Earth as a whole (Section 16.6). These are the free

oscillations, standing waves of long wavelength.

Similarly, surface waves (Section 16.5) of long

wavelength are better treated as free modes for

which the sphericity of the Earth is properly

taken into account. The free oscillations now

have a prominent role in modelling the Earth.

Synthetic seismograms are calculated as

weighted sums of the normal modes, where the

weights are determined by the elements of the

moment tensor of an earthquake multiplied by

the strains of the modes calculated at its location

(Section 16.7). When modes are added in this way

they simulate a total seismic record, which is

seen to progress from identifiable P, S and sur-

face waves through to reverberations of the

Earth as a whole as the higher frequencies die

away. Inversion of seismograms observed at sta-

tions of the global network using normal mode

synthetics is now routine, and provides a cata-

logue of moment tensors for earthquakes

worldwide.

16.2 Body waves

As the words imply, body waves are transmitted

through the interior of the Earth. In a uniform

body they would spread out as spherical wave-

fronts, but heterogeneities in the Earth refract

and reflect them in numerous ways. The study of

travel times of body waves to different distances

led to our understanding of the Earth’s internal

structure (Chapter 17). They are easier to com-

prehend than the surface waves that are con-

strained to follow the surface and the layering

close to it. The two kinds of body wave are

referred to as P-waves and S-waves. P is simply

the initial for primary, because P-waves arrive

first. S (secondary) waves are slower. P-waves

are compressional waves, involving alternating

compressions and rarefactions of a medium, and

are transmitted by liquids and gases as well as

solids. The particle motion is in the direction of

propagation. S-waves are shear waves, with par-

ticle motion transverse to the direction of prop-

agation. They are transmitted only by solids. In

the case of S-waves, different polarizations are

distinguished, the plane of polarization being

the plane containing the directions of propaga-

tion and particle motion. If the plane of polar-

ization is vertical, the waves are designated SV,

and if the particle motion is horizontal they are

termed SH. These polarizations behave differ-

ently at horizontal boundaries.

The speed of a body wave in any medium is

given by the square root of the ratio of an elastic

modulus to the density. In each case the relevant

modulus is the one appropriate to the material

deformation. Definitions of elastic moduli and

relationships between them are given in

Section 10.2 and Appendix D. In an isotropic

solid the P-wave speed is

ﬃﬃﬃﬃﬃﬃﬃﬃ

=

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

Kþ





=

; (16:1)

and the S-wave speed is

ﬃﬃﬃﬃﬃﬃﬃﬃ

=

: (16:2)

Since S-waves cause pure shear of a transmitting

medium, Eq. (16.2) is correspondingly simple,

but the P-wave speed (Eq. (16.1)) is less obvious.

A sound wave in fluid causes alternating com-

pressions and rarefactions that are hydrostatic,

because the medium supports no shear stress.

The modulus is therefore incompressibility

(bulk modulus), K, and Eq. (16.1) applies with

 ¼0. Since compression in one direction

involves material deformation in solids it is

resisted by  as well as by K. Consider first the

transmission of a compressional wave along a

rod that is thin compared with the wavelength

of the wave. The compressions and rarefactions

of the rod are then accompanied by transverse

strains, so that each section dilates or contracts

laterally by Poisson’s ratio times the longitudinal

compression or extension. The wave speed is

ﬃﬃﬃﬃﬃﬃﬃﬃ

E=

, where E is Young’s modulus for the

240 SEISMIC WAVE PROPAGATION

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D

–

241

– [239–266] 13.3.2008 11:41AM

material. This is the most commonly considered

elastic modulus and is sometimes referred to

by engineers as the elastic modulus. It may be

measured for the material of a wire simply

by stretching the wire. Now consider waves of

progressively shorter wavelengths. When the

wavelength is not much greater than the rod

diameter the lateral contractions and dilations

of adjacent sections (half-wavelengths) of the rod

are no longer independent but oppose one

another, and when the wavelength is very short

compared with the diameter they are prevented

from occurring at all. Then the modulus describ-

ing the axial compressions and dilations by the

wave is the modulus of axial strain, , which is

related to the other moduli by expressions in

Appendix D. It exceeds Young’s modulus, E,by

a factor that depends on Poisson’s ratio, ,

because axial strain becomes harder when the

lateral response is prevented. In the Earth, wave-

lengths of P-waves are normally very short com-

pared with the dimensions of the Earth or of its

major layers and so the P-wave modulus is .

Since there is a greater fundamental interest in

the bulk modulus, K, it is convenient to replace 

by ðK þ 4=3Þ, as in Eq. (16.1).

In an isotropic medium a seismic wave tra-

vels in a direction normal to the wavefronts, lead-

ing to the concept of seismic rays. This is useful in

describing the propagation of body waves

through internal layers or features of the Earth

that are large compared with the wavelength. As

in optics, ray theory is applicable only to situa-

tions in which wavelength is short compared

with features of interest. Otherwise diffraction

is important, requiring a wave theory.

Angles of refraction and reflection of seismic

rays at material boundaries in the Earth are rep-

resented by equations that are exact analogues of

the laws of optical reflection and refraction. With

respect to the fraction of incident energy that is

reflected or refracted, the seismic situation

requires allowance for P to S and S to P conver-

sions, which have no optical equivalent. But, as in

optics, refraction occurs, however gradual the

transition in wave speeds between media,

whereas reflection, and wave conversion in the

seismic case, diminish as the thickness of a tran-

sition becomes comparable to the wavelength.

Consider the refraction of a plane wave at a

plane boundary, as in Fig. 16.1. Each point in a

wavefront may be regarded as a source for fur-

ther propagation of the wave (Huygens’s princi-

ple) and the distance travelled in time Dt is

proportional to the wave speed, which is differ-

ent in the two media, as illustrated. The angles i

and i

are related by considering the triangles

ABC and ABD. Thus

sin i

¼ BC=AB ¼ v

t=AB (16:3)

and

sin i

¼ AD=AB ¼ v

t=AB; (16:4)

so that

sin i

: (16:5)

This is Snell’s law of refraction.

Similar constructions may be used for reflec-

tion and wave conversion. For a simple reflection

there is no change in wave speed and so the

angles of incidence and reflection are equal.

Medium 1

(velocity v

)

Medium 2

(velocity v

)

+ Δt

Δt

FI G U R E 16.1 Huygens’s

construction for refraction of a wave at

a plane boundary. Positions of a

wavefront at times t

and ðt

þ tÞ are

shown by broken and solid lines and

arrows on the rays show the direction

of propagation. Each point on the

wavefront at t

acts as a source of

wavelets (shown as short arcs), the

envelope of which is the wavefront

at ðt

þ tÞ.

16.2 BODY WAVES 241

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D

–

242

– [239–266] 13.3.2008 11:41AM

When partial conversion of a wave occurs, as

illustrated in Fig. 16.2, then the speeds of the

incident and converted waves, whether refracted

or reflected, are used in Snell’s law (Eq. (16.5)).

For the wave speeds V

(for P-waves) and V

(for

S-waves) in media 1 and 2, as in Fig. 16.1, the law

becomes

sin i

sin r

sin f

¼ p; (16:6)

where p is the ray parameter for the family of

rays. Particular reflections or refractions cannot

occur if this equation would require the sines of

the relevant angles to exceed unity. Thus, a wave

may be totally internally reflected in medium 1 if

sin r

, sin f

and sin f

all exceed unity, although

continuity of particle motion at the boundary

requires participation by a layer of medium 2

with a thickness comparable to the wavelength.

The inverse velocity (1/V ) is referred to as the

slowness. Snell’s law, Eq. (16.6), shows that the

family of rays has a common horizontal compo-

nent of slowness, given by p.

The incident wave considered in Fig. 16.2 is

an SV-wave, a shear wave in which the plane of

polarization or particle motion is vertical. This

gives it a component of motion normal to a

horizontal boundary. It is this component of

the motion that generates P-waves at the boun-

dary. An SH-wave, in which particle motion is

parallel to the boundary, causes no compres-

sions or rarefactions across the boundary and

so can be refracted and reflected only as an

SH-wave. Conversely, P-waves incident on a

boundary generate both reflected and transmit-

ted SV-waves, but no SH-waves. In general S-

waves have both SV and SH components, but if

a wave arrival at a seismic station is observed to

be of pure SV type, then it is probably a conver-

sion from a P-wave at an internal boundary.

Snell’s law is a consequence of Fermat’s prin-

ciple that the travel time for a seismic wave

between source and receiver along a ray path is

stationary with respect to adjacent paths. In

most cases the stationary point is a minimum.

However, for reflection from a free surface it is a

maximum relative to adjacent incident angles

(Problem 16.2). In heterogeneous media the

Fermat path is found by ray-tracing methods

that vary the path until travel time is a

minimum.

16.3 Attenuation and scattering

Plane seismic P-waves satisfy the equation of

motion given in general form as Eq. (11.48). For

propagation in one direction in an isotropic

medium we obtain the familiar wave equation



¼ 

: (16:7)

This equates the force per unit volume (left-hand

side) to the mass per unit volume times accelera-

tion (right-hand side) and  ¼ l þ 2 ¼ K þð4=3Þ

Incident SV

Reflected SV

Reflected P

Refracted P

Refracted SV

Medium 1

= i

Medium 2

FI G U R E 16.2 Reflected and refracted

rays derived from an SV ray incident on

a plane boundary. The boundary is

assumed to be ‘welded’, that is, there is

a continuity of solid material across it.

242 SEISMIC WAVE PROPAGATION

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D

–

243

– [239–266] 13.3.2008 11:41AM

is the P-wave elastic modulus (Eqs. (16.1), (11.14),

(11.16)). u is the displacement in the direction

of propagation, and  is the density. Solutions

to the wave equation can be written

u ¼ f ðx  ctÞor f ðx þ ctÞ depending on whether

the wave is travelling in the positive or negative

x-direction respectively, where c is speed.

Differentiation and substitution in Eq. (16.7)

gives c ¼

ﬃﬃﬃﬃﬃﬃﬃﬃ

=

. An arbitrary pulse can be repre-

sented as a sum of sinusoids (Fourier transform)

but incorporation of attenuation or wave decay

requires additional exponential factors. It is com-

mon practice in seismology to represent f in

terms of complex exponentials, expði!tÞ, with

both real and imaginary components. Particle

displacement for a wave travelling in the posi-

tive x-direction can be written

u ¼ A exp½iðkx  !tÞ; (16:8)

where, if there is no attenuation, wave number is

simply k ¼ !=c. If the medium is attenuative, k is

complex. It is convenient to retain k as the real

component and add an imaginary term: k þ i.

Then we can write

u ¼ Ae

x

exp½iðkx  !tÞ; (16:9)

which decays exponentially with distance,

where  is known as the attenuation coefficient.

This can be written in terms of the Q of the

medium as  ¼ !=2cQ (Eq. (10.21)).

As explained in Section 10.7, attenuation, that

is non-zero  or 1=Q , causes dispersion (except for

the special case Q / !). This is a consequence of

the requirement that a pulse should be causal,

with no feature travelling faster than the wave

speed. The general expression relating frequency

dependences of wave speed and attenuation is

the Hilbert transform in Eq. (10.30). When Q and

k vary, ray-tracing methods are used to find the

ray path, and attenuation effects are integrated

along the ray.

Amplitude also decreases by geometric

spreading. An expanding curved wavefront

diminishes in amplitude as 1/(radius of curva-

ture). Conversely, a contracting curved wave-

front focusses energy. The amplitude variation

is simple if the radius of curvature is very large

compared with the wavelength, but if not, then a

more general treatment is required to take

account of diffraction. We adopt the solution

from the equivalent optical problem (Born and

Wolf, 1965, p. 441). The amount of focussing

depends on the ratio of the aperture to the wave-

length, l,as

Að0Þ=Aðr

Þ¼

; (16:10)

where AðrÞ is amplitude at distance r from the

focus, 2R is the aperture (chord) of a wavefront in

the form of a spherical cap of radius of curvature

. As shown below (Eq. (16.14)), this is propor-

tional to the ratio of the aperture area (pR

) to the

area of the inner Fresnel zone (pr

l), within

which wave interference is constructive.

An essential feature of Eq. (16.10) is focusing

that depends on wavelength. This is not related

to dispersion and requires no frequency varia-

tion of seismic velocity, but is a consequence

of diffraction. This phenomenon o ffers an

explanation for concentrated patches of damag-

ing intensity in Santa Monica, California,

caused by the 1994 Northridge M 6.7 earth-

quake, which had an epicentre 21 km away,

too distant to have caused the damage without

strong focusing (Davis et al., 2000). Santa Monica

sits on a deep (3 km) basin of sediment with

an S-wave speed about half that of the base-

ment rock. Irregularities in the boundary of

the basin act as lenses, with dimensions (aper-

tures) of order 1 km, focusing the arriving waves

on patches determined by the direction of

arrival. The f ocusing is frequency dependent,

allowing the positions and d imensions o f sev-

eral such lenses to be calculated from

Eq. (16.10).

Scattering of seismic waves from heterogene-

ities in an elastic medium causes amplitude

decay additional to that arising from anelastic

damping, which is discussed in Section 10.5.

When a wave encounters elastic heterogeneities,

energy is scattered in all directions, reducing the

forward travelling energy. We identify separate

scattering (s) and intrinsic (i) components of the

attenuation coefficient:

 ¼ 

þ 

(16:11)

16.3 ATTENUATION AND SCATTERING 243

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D

–

244

– [239–266] 13.3.2008 11:41AM

where ‘intrinsic’ implies a material property,

that is local conversion of elastic energy to

heat. Equivalently, the total Q is given by

: (16:12)

Analytical calculation of scattering coefficients

is possible only for simple heterogeneities, such

as a spherical contrast or a crack. Most analyses

deal with single scatterers and sum the scattered

fields from multiple scatterers spread through-

out a homogeneous medium. This is adequate if

the density of scatterers is low. However, the full

problem involves multiple scattering, in which a

single-scattered field interacts with other scatter-

ers generating secondary fields. The secondary

fields interact again, and so on in an infinite

series, but because the amplitude of the scat-

tered wave depends on the contrast in proper-

ties, which in the Earth is usually not very large,

the series converges rapidly.

The amount of scattered energy depends on

the impedance contrasts and the sizes of the

scatterers relative to the wavelength of the seis-

mic waves. Treatments of scattering appeal to

methods of full wave theory rather than ray

theory (Section 16.2). Ray theory effectively

assumes that the frequency of the radiation is

infinite. In reality, seismic wave pulses are com-

posed of a range of frequencies and associated

wavelengths. Ray theory is applicable if the

length-scale of the region under investigation is

large compared with the wavelengths, otherwise

the different frequency components are scat-

tered differently and finite frequency effects

must be taken into account. The forward pro-

pagation of a finite frequency wave can be cal-

culated by summing Huygens wavelets, as

considered in determining Snell’s law in

Section 16.2. Consider a point A on the wave-

front of a plane wave connected by the most

direct ray to a point B at distance h in front of

the wave. The amplitude at B depends on those

wavelets that constructively interfere with the

wavelet from A. Let C be a point on the wavefront

a distance y from A. Wavelets from C will be

increasingly out of phase with those from A as

the distance AC (i.e., y) increases. The phase dif-

ference is given by

d ¼ 2pð

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

þ y

 hÞ=l  py

=hl:

(16:13)

Provided d  p, the wavelets interfere construc-

tively. This condition defines the first Fresnel

zone as



ﬃﬃﬃﬃﬃ

: (16:14)

The higher-order Fresnel zones correspond to 2l,

3l, ... path differences but cancel out (Sheriff

and Geldart, 1982), so the amplitude and travel

time at B are most affected by heterogeneities in

the cone that includes B and the first Fresnel

zone.

The effect of a heterogeneity at A depends on

its size relative to the first Fresnel zone. If the

size of the heterogeneity is a  y

, it has negli-

gible effect, whereas if a  y

it has maximum

effect. For a plane wave that passes through a

spherical heterogeneity a patch of the down-

stream wavefront becomes bowed inwards or

outwards depending on whether the velocity in

the heterogeneity is lower or higher than in the

surroundings. As the wave progresses, ampli-

tudes exhibit focusing or defocusing as the

perturbed wavefront contracts or expands.

Scattering effects that are seen in the near-

field, h  a, may be appreciable, but at greater

distances the Fresnel zone enlarges as

ﬃﬃﬃ

, and

the importance of the wavelets that pass though

the scatterer diminishes compared with those

from the remainder of the Fresnel zone. The

disturbance heals in the far-field as the effects

of the scatterer diminish. This process, called

diffractive healing, occurs as wavelets from the

part of the Fresnel zone that lies outside of the

scatterer dominate the total. At large distances

the plane wavefront is restored. Diffractive heal-

ing accounts for the difficulty in imaging hot

spot plume stems (Chapter 12) deep in the man-

tle where they are small compared with

ﬃﬃﬃﬃﬃ

. For

example, if the seismic wavelength is 10 km, for

observations at a distance h ¼4000 km, the

plumes need to have radii larger than 200 km

to be observable. While images of much larger

features such as plume heads are observable

at these distances, plume stems smaller than

ﬃﬃﬃﬃﬃ

require near-field measurements. Such

diffractive healing is important for seismic

244 SEISMIC WAVE PROPAGATION

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D

–

245

– [239–266] 13.3.2008 11:41AM

tomography of the crust and uppermost mantle,

for which it is assumed that waves from distant

earthquakes travelling through relatively homo-

geneous mantle have been healed to nearly

plane waves.

If, instead of a propagating plane wave, we

consider spherical waves travelling between a

point source and a receiver, the Fresnel zones

vary with distance along the ray path

(Fig. 16.3(a)). Let the total path length be L, and

consider a point at distance x along the ray with y

measured at right angles to it. The phase differ-

ence between the Huygens wavelet that travels

from the source at x ¼ 0 via y to the receiver at L

and the wavelet travelling directly along the ray

path is

d ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

þ y

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ðL  xÞ

þ y

 L





x 1 þ



þðL  xÞ 1 

ðL  xÞ

 L



ðL  xÞ



: ð16:15Þ

Again, for constructive interference d

p,so

that

¼½lðL=x  1Þ

1=2

: (16:16)

The region traced out by y

ðxÞ,theFresnel volume,

is an ellipsoid-like volume about the ray

(Fig. 16.3(b)). Wavelet contributions from the

higher order Fresnel volumes (Fig. 16.3(b)) alter-

nate between rapidly varying positive and nega-

tive interferences and so cancel out. Variations in

properties within the inner Fresnel zone have

greatest effect on both amplitude and phase of a

seismic signal. Now we consider a typical seismic

pulse. It is composed of a band of frequencies,

each with a corresponding range of Fresnel

zones. As a result, the perturbation of phase and

amplitude is an integral of a sensitivity kernel

K(r) times the velocity perturbation field v(r)

over the volume, with maximum contributions

from the inner Fresnel volumes corresponding

to each wavelength (Spetzler and Snieder, 2004).

Because the signal is band-limited, heterogenei-

ties along the ray path that do not extend signifi-

cantly into the Fresnel zone of the highest

frequency component have negligible effect on

the waveform. Fluctuations in this region are

instead subject to diffractive healing. This gives

rise to what has been termed the ‘banana doughnut

paradox’ by Marquering et al. (1999). The banana

represents the ellipsoidal averaged Fresnel vol-

ume about a curved ray. The doughnut is a cross-

section across the ray with hole smaller than the

inner Fresnel zone associated with the highest

frequency component. Thus, the ray itself traces

out the locus of insensitivity to small-scale hetero-

geneities. Ray theory suggests the opposite; that

changes lying along the ray should be observed at

the receiver. In fact this assumption has been the

basis for most tomographic interpretations. The

paradox can be reconciled if one recognizes that

ray theory used with finite- rather than infinite-

frequency signals applies to heterogeneities

much larger than the wavelength. To be detect-

able the heterogeneity must extend over the

Fresnel volume either side of the ray, and this in

turn is determined by the frequencies used.

From this discussion we see that objects that

are small relative to the wavelength cause little

x = 0

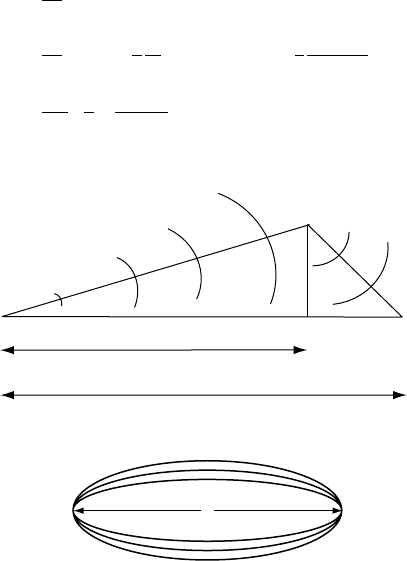
FI G U R E 16.3 (a) Interference of Huygens wavelets. The

phase difference between the direct wavelet and one

that is diffracted from Y must be less than 180

for the

wavelets to add constructively. (b) Fresnel volumes, as

represented by Roth et al. (1993). These are zones in

which direct and diffracted wavelets, travelling from

the source (r

) to the receiver r

, interfere alternately

constructively and destructively.

16.3 ATTENUATION AND SCATTERING 245

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D

–

246

– [239–266] 13.3.2008 11:41AM

scattering. As an extreme example, at the small-

est scales seismic waves are not affected by crys-

tal structures or grain distributions and the

medium can be treated as homogeneous. Large

objects can be treated by ray theory and ana-

lysed as piecewise homogeneous (Section 16.4).

Scattering is most effective when the sizes of

heterogeneities are comparable to that of the

Fresnel zone. Seismic waves passing through a

medium with random scatterers are most at-

tenuated at frequencies for which associated

Fresnel zones are equal to the mean size of the

scatterers. For example, seismic body waves with

frequencies of about 1 Hz are strongly scattered

in the crust and upper mantle (Dainty, 1990;

Padhy, 2005), giving rise to a band of attenuation

at about 1 Hz. In a uniform, infinite, non-scattering

medium, the S-wave pulse from an earthquake

becomes zero after a time equal to the sum of

rise time and propagation time of the rupture

(Section 14.2), which is typically a few seconds

for an earthquake of magnitude 6. However,

reverberations, called coda, are observed to go

on for many minutes. They are caused mainly by

S–S scattering from heterogeneities (Aki, 1969;

Zeng, 1993), and are thought to be comprised

of back-scattered arrivals from an expanding

hemi-ellipsoidal surface with foci at source and

receiver. This ellipsoid maps the locus of scat-

terers for which travel times (source–scatterer–

receiver) are equal for all scatterers along its

boundary. As time progresses and the scattering

ellipsoid grows proportionately, the coda decays

by geometric spreading and intrinsic attenua-

tion. Fresnel zones for 1 Hz S-waves in the crust

(l  3 km) travelling typical distances of 30 km

have a dimension of 10 km. That many geologic

features, such as folded sediments and basins,

are of this size may explain the 1 Hz ‘absorption’

band.

Recent advances in recording and processing

digital seismic data from global and regional

seismic networks have facilitated the study of

scattering in the mantle and core. Haddon

(1972) first suggested that precursive wave trains

that build up before PKP body-wave phases were

caused by scatterers in the mantle, and Haddon

and Cleary (1974) concluded that they are con-

centrated in the D

region. Vidale and Hedlin

(2000) drew attention to sources of scattering

near the core–mantle boundary (CMB) north of

Tonga, requiring such large impedance contrasts

that they have been presumed to include pockets

of partial melt (but see an alternative interpreta-

tion in Sections 17.7 and 23.4). In addition to

heterogeneities near the CMB there is a growing

body of evidence for scatterers distributed

throughout the mantle (Haddon et al., 1977).

Isolated scatterers observed in the mid-mantle

may be delaminated slabs of subducted litho-

sphere (Kaneshima and Helffrich, 1999). Often

the interpretation of the scattering in the mantle

is not unique and a full description of the three-

dimensional distribution of scatterers requires

more information (Hedlin and Shearer, 2000;

Earle and Shearer, 2001).

While the fluid outer core is observed to be

homogeneous, scattered arrivals have been iden-

tified from the upper regions of the inner core

(Vidale and Earle, 2000). The scattered signals

from the inner core have been used to estimate

inner core rotation. Using seismograms from

Russian nuclear explosions recorded on an array

in North America, Vidale et al.(2000)separated

signals in the coda into those generated by scat-

tering from the east and west sides of the inner

core. They were able to show that the phase differ-

ence between east and west arrivals changed with

time in a manner consistent with super-rotation

of the inner core relative to the mantle. The inferred

rate, <0.28/yr, is consistent with the other esti-

mates, as discussed in Sections 17.9 and 24.6.

Waves generated in a high-velocity slab tend

to scatter out of the slab and so decay rapidly

with distance. In contrast, waves generated in a

low-velocity slab become trapped as angles of

incidence at the boundaries become greater

than the angle of critical internal reflection.

Thus, it was surprising to find that earthquake

waves generated in the subducting slab beneath

Japan have higher amplitudes on the surface

above the slab than expected from scattering,

suggesting trapping of energy in the slabs.

Furumura and Kennett (2005) showed that this

can be explained by internal heterogeneities,

such as high- and low-velocity laminations in

the slab, that trap energy to form slab-guided

waves. In a similar fashion scatterers in the

246 SEISMIC WAVE PROPAGATION