Stacey F.D., Davis P.M. Physics of the Earth
Подождите немного. Документ загружается.


//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C06.3D
–
87
– [81–89] 13.3.2008 10:37AM
For surface material of ‘standard reference den-
sity’ 2670 kg m
3
, the Bouguer gradient becomes
0.1967 mGal m
1
. Neither of these methods is
satisfactory where there is more than slight topo-
graphy and in general detailed topographic cor-
rections are needed.
A comparative glance at continent-scale free-
air and Bouguer anomaly maps shows that the
free-air anomalies are generally much smaller.
This is evidence for continental scale isostatic
balance, by which surface elevation is compen-
sated by reduced density at depth. Isostasy is
considered further in Section 9.3. On a scale of
100 km or less, free-air anomalies may be much
greater, because they can be supported by the
strength of the lithosphere (the cool uppermost
100 km or so of the Earth).
6.4 The approach to equilibrium
ellipticity
As indicated in Section 6.1, there are four causes of
an excess ellipticity of the Earth, relative to hydro-
static equilibrium. It is not a simple matter to iso-
late them for independent study. But, although
calculation of the equilibrium ellipticity itself is
mathematically tricky, it is not subject to question.
The complexity of the problem arises from the fact
that, although the surfaces of equal density are
equipotentials, their ellipticities decrease with
depth. The basic reason for this can be seen by
considering the equilibrium flattening of a rotating
body of uniform density as in Problem 6.4, which
shows that flattening is proportional to
1
.This
means that in a body such as the Earth, in which
density increases with depth, the ellipticities of the
equipotential surfaces are affected by the material
above as well as below the surfaces and so cannot
be written in terms of a straightforward integral.
An approximate first order theory (e.g.
Jeffreys, 1959) yields the equilibrium (hydro-
static) flattening
f
H
¼
5=2ðÞm
1 þ 5=2ðÞ1 3=2ðÞC=Ma
2
ðÞ½
2
; (6:39)
where m is given by Eq. (6.32). A higher-order
treatment, with resort to numerical methods, is
necessary to obtain a value that allows a satisfac-
tory comparison with the observed flattening.
Nakiboglu (1982) gives
f
H
¼ 1=299:627 ¼ 3:337 48 10
3
(6:40)
with corresponding hydrostatic geoid coefficients
J
2H
¼ 1:072 70
1
10
3
; (6:41)
J
4H
¼2:992 10
6
: (6:42)
Comparison of Eqs. (6.23) and (6.40) gives an
excess flattening, relative to hydrostatic equili-
brium, of 0.5%, which corresponds to a differ-
ence in equatorial and polar radii 100 m greater
than equilibrium. We can note that if equili-
brium is assumed then Eq. (6.39) allows an esti-
mate of the moment of inertia from the surface
flattening. On this basis the observed flattening
of the Earth gives C/Ma
2
¼0.3309, which is quite
close to the measured value, 0.3307. Thus, it is
reasonable to apply Eq. (6.39) to Mars, for which
observations of precession give a value of the
moment of inertia, to show that, within the
accuracy of observations, it has an equilibrium
ellipticity.
The dynamic oblateness, J
2
, (Eq. 6.14), is
slowly decreasing as the Earth adjusts to dimin-
ished polar ice caps. Cox and Chao (2002) have
documented this effect, pointing out that for two
decades of precise measurement, 1979–1998,
there was a more or less steady rate of change,
dJ
2
/dt 2.8 10
11
per year, but that for four
years, 1998–2002, the trend was temporarily
reversed. Chao et al. (2003) suggested that this
could be explained by a climatically driven
decade-scale oscillation in the Pacific Ocean.
The earlier trend has resumed and is interpreted
as the long-term effect attributable to post-glacial
rebound, a topic of Section 9.5.
The total excess J
2
, DJ
2
¼9.9 10
6
, the differ-
ence between Eqs. (6.14) and (6.41), suggests a
very long relaxation time, DJ
2
/(dJ
2
/dt) ¼350 000
years, but this is meaningless. We need to con-
sider more carefully what DJ
2
means. As men-
tioned in Section 6.1, there are four causes of
the excess ellipticity and not all of them can be
considered as departures from equilibrium. The
tidal effect, that is the ellipticity resulting from
6.4 THE APPROACH TO EQUILIBRIUM ELLIPTICITY 87

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C06.3D
–
88
– [81–89] 13.3.2008 10:37AM
the difference between the tidal potential at the
poles and the average on the equator (Chapter 8)
must obviously be subtracted, but only reduces
the effective DJ
2
by 1.0 10
8
. The contribution
to dJ
2
/dt by slowing rotation, caused by tidal
friction (Chapter 8) is seen to be negligible by
noting that d ln !/dt ¼2.8 10
10
year
1
and
that the equilibrium J
2
varies with rotational
speed ! as !
2
,sothat(dlnJ
2
/dt)
tidal
¼5.6 10
10
year
1
and therefore (dJ
2
/dt)
tidal
¼6 10
13
year
1
. For any plausible lag of the flattening
this corresponds to a negligible contribution to
DJ
2
. In fact it is smaller than the human contribu-
tion to dJ
2
/dt caused by impoundment of water in
reservoirs, for which Chao (1995) gives a mini-
mum estimate of 1 10
12
year
1
.
The major problem is heterogeneity of the
mantle and the fact that the Earth self-adjusts its
orientation to minimize rotational energy by
aligning the heterogeneities to maximize the
moment of inertia about the rotational axis.
We have no reliable way of estimating the result-
ing contribution to DJ
2
, but an idea of how
big it is likely to be is obtained from the ellipti-
city in the equatorial plane. From the spherical
harmonic coefficients of the gravitational
potential in Table 9.1 we see that the coefficien ts
representing equatorial ellipticity give
[(C
2
2
)
2
þ(S
2
2
)
2
] ¼2.8 10
6
,comparedwiththe
excess axial ellipticity, 4.4 10
6
,obtainedfrom
the difference between observed and equilibrium
values of C
2
0
. Thus, subtracting the equilibrium
ellipticity, we see the Earth as a triaxial ellipsoid
with moments of inertia C > B > A such that (C B)
and (B A) are comparable. This is what would
be expected statistically, so we have no basis for
supposing that more than a small fraction of
the excess ellipticity is attributable to glacial
depression and we have no direct way of estimat-
ing the magnitude of this fraction. Note that
Eqs. (6.11)to (6.18) assume Eq. (6.10) and therefore
that the value of A is really (A þB)/2.
The observed progressive decrease in J
2
gives
a tantalizing glimpse of deep mantle rheology. If
the component of DJ
2
representing residual gla-
cial depression of the poles were precisely
known, then its decay, together with the other
low order geoid harmonics (Chapter 9), would
give a measure of the depth variation of mantle
viscosity. Mitrovica and Peltier (1993) and Han
and Wahr (1995) discussed this problem, con-
cluding that available data did not suffice for a
clear conclusion, and it remains true that there is
no satisfactory independent evidence of DJ
2
.
However, post-glacial rebound does provide esti-
mates of mantle rheology and most recent stud-
ies agree that there is an increase in viscosity
with depth in the mantle by a factor of order
100 (e.g. Mitrovica and Forte, 1997; Kaufman
and Lambeck, 2000).
Variations in J
2
and in the rotation rate are
linked. In considering the effect of the tidal slow-
ing, we can apply Eq. (6.20) to the hydrostatic
state of the Earth and see that both f and J
2
vary
with rotation in the manner of m, which depends
on !
2
. Thus the equilibrium value of J
2
, that is J
2H
,
is proportional to !
2
and so the variation caused
by the slowing rotation is
1
J
2H
d J
2H
dt
¼
2
!
d!
dt
: (6:43)
With the total slowing by lunar and solar tides
given by Eq. (8.31), ! ¼6.5 10
22
rad s
2
, this
yields
d J
2H
=dt ¼1:9 10
20
s
1
¼6:1 10
13
year
1
:
(6:44)
This is below the level of detectability. If we can
estimate the time constant, , for relaxation of
the excess ellipticity, then the excess attribut-
able to the slowing rotation is
J
2!
¼ dJ
2H
=
dtðÞ: (6:45)
For 10
4
years, J
2!
6:1 10
9
, which is
close to the resolution limit for measurements
of J
2
and is not a significant effect.
Now consider the change in rotation rate
due to the variation of J
2
caused by the post-
glacial rebound (Section 9.6). The angular
momentum of the Earth is conserved in this
process, so that
dðC!Þ=dt ¼ 0; (6:46)
where C is the axial moment of inertia, and
therefore
_!=! ¼
_
C=C: (6:47)
88 ROTATION, FIGURE OF THE EARTH AND GRAVITY

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C06.3D
–
89
– [81–89] 13.3.2008 10:37AM
In relating this to
_
J
2R
, the rebound component
of dJ
2
/dt, it is convenient to introduce the para-
meter C=Ma
2
ðÞ¼0:330 695, because this is deter-
mined by the Earth’s density profile and is not a
function of time (i.e. C /a
2
). Then, rewriting the
definition of J
2
(Eq. 6.14),
J
2
¼
C A
Ma
2
¼ 1
A
C
C
Ma
2
; (6:48)
and noting that
_
A ¼
_
C=2, we have
_
J
2R
¼
_
C
C
1
2
þ
A
C
C
Ma
2
¼ 0:4948
_
C
C
: (6:49)
Thus, by Eq. (6.47), there is a rebound component
of rotational acceleration
_
! ¼!
_
C=C ¼2:02!
_
J
2R
: (6:50)
Identifying
_
J
2
¼2:8 10
11
year
1
with
_
J
2R
we have a rebound component of rotational
acceleration
_
!
R
=! ¼ 5:7 10
11
year
1
¼1:8 10
18
s
1
; (6:51)
and therefore
_
!
R
¼ 1:3 10
22
rad s
2
: (6:52)
This opposes the frictional slowing by Eq. (8.31),
_
!
tidal
¼6:5 10
22
rad s
2
, giving a net slowing
_
! ¼5:2 10
22
rad s
2
.
In addition to the tidal and rebound contribu-
tions to
_
! there are irregular effects of angular
momentum exchange with the atmosphere,
oceans and core, but if we consider an average
over 1000 years or more we have some prospect
that these short-term effects are averaged out.
This is the approach of Stephenson and
Morrison (1995), who concluded, from 2000
years of eclipse data, that allowance for the
rebound effect removed what would otherwise
be a discrepancy in tidal friction observations.
However, the rotational effects of glaciation
and rebound occur over thousands to tens of
thousands of years and are brief transients on
the time scale of tidal friction which acts over
the entire life of the Earth (Sections 8.3, 8.4).
6.4 THE APPROACH TO EQUILIBRIUM ELLIPTICITY 89
//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C07.3D
–
90
– [90–101] 13.3.2008 10:36AM
7
Precession, wobble and rotational
irregularities
7.1 Preamble
The axis of the Earth’s rotation is inclined to the
pole of the ecliptic (normal to the orbital plane) by
23
o
.45. This gives us the seasons. But the axis does
not maintain a constant orientation in space.
Gravitational interactions between the equatorial
bulge and the Moon and Sun cause a slow preces-
sion of the axis about the ecliptic pole. The axis
describes a cone with a 478 angle in a period of
25 730 years, fast enough for precise astronomical
measurement, but not so fast that navigation by
the stars is seriously inconvenienced. This is the
most obvious of the complications to simple rota-
tion. In an illuminating survey of the history of
the subject, Ekman (1993) notes that the preces-
sion was observed by Hipparchus, who, in about
125 BC, reported a measure of its rate in remark-
able agreement with modern estimates.
To see how the precession arises, consider a
small satellite in a circular orbit that is inclined
to the equatorial plane. Since the Earth is not
spherical, its gravitational force on the satellite
is directed precisely towards the centre of the
Earth only when the satellite is above the equa-
tor (or, of course, one of the poles if it is in a polar
orbit). At intermediate latitudes the latitude var-
iation of gravity imparts a torque tending to pull
the satellite orbit towards the equatorial plane.
The torque acts in a sense perpendicular to the
angular momentum vector, causing a precession
of the orbit. The points at which the orbit crosses
the equatorial plane are referred to as nodes. As
seen in space, not relative to the rotating Earth,
they drift progressively in a prograde sense, east-
wards for a satellite with a west-to-east compo-
nent of orbital motion. The rate of this drift gives
a precise measure of the Earth’s ellipticity, as
represented by the coefficient (Eq. 6.14)
J
2
¼ðC AÞ=Ma
2
¼ 1:082 626 10
3
; (7:1)
where C, A are the moments of inertia about
polar and equatorial axes and M, a are the mass
and equatorial radius. There is a corresponding
opposite torque on the Earth, but for a man-
made satellite this is not significant.
The same principle applies to interactions
with the Sun and Moon, but in these cases
there is a noticeable effect on the Earth. The
torque, proportional to (C A), acts on the
Earth’s rotational angular momentum, C!,so
that the rate of the resulting precession provides
a measure of the quantity known as the dynam-
ical ellipticity:
H ¼ðC AÞ=C ¼ 3:273 79 10
3
¼ 1=305:4567:
(7:2)
Combining Eqs. (7.1) and (7.2) we obtain the
moment of inertia coefficient
C=Ma
2
¼ J
2
=H ¼ 0:330 698: (7:3)
This is a measure of the density profile of the
Earth. For a uniform sphere the value would be 0.4
and the smaller value in Eq. (7.3) is a measure of
//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C07.3D
–
91
– [90–101] 13.3.2008 10:36AM
the concentration of mass towards the centre. The
moments of inertia of other bodies in the Solar
System are mentioned in Eq. (1.17) and Table 1.2.
The result in Eq. (7.3) was first used in modelling
the Earth by K. E. Bullen in the 1930s and remains
an important parameter that any model must
match, in the same way as the total mass must
agree with the observed mass (Section 17.6).
The dynamical ellipticity, H, appears also in
the explanation of another phenomenon, the
Chandler wobble (Section 7.3). This is a motion
of the Earth that involves no interaction with
any other body. It arises because the rotational
axis departs by a small angle, , normally about
0.15 arcsec (0.7 microradian) from the symmetry
axis, which is the axis of maximum moment of
inertia. This means that the rotational energy
exceeds the energy of symmetrical rotation
with the same angular momentum by an amount
proportional to
2
. The resulting gyroscopic tor-
que tends to turn the Earth so that its symmetry
axis coincides with the axis of angular momen-
tum (which remains fixed for the purpose of this
discussion because we are considering an effect
that is entirely internal to the Earth). The torque,
acting on the angular momentum, causes a pro-
grade precession of the rotational axis about the
angular momentum axis that is apparent as a
cyclic variation of latitude.
For a rigid Ea rth the wobble period would be
1/H days ¼305 days (see Eq. (7.2)). This was the
period sought for many years before the discov-
ery, by S. C. Chandler in 1891, of the observed
period, about 432 days. The difference is explained
by the elastic deformation of the Earth, with
accompanying responses of the oceans and core
to the gyroscopic torque. The deformation par-
tially adjusts the equatorial bulge towards sym-
metrical rotation, reducing the torque and so
lengthening the period of the motion. Thus, the
wobble provides a measure of the global average
rigidity of the Earth, a check on the elasticity
inferred from seismology (Chapter 17).
The wobble is damped with a time constant of
about 30 years (Eq. (7.25)), which means that it
must be continuously maintained. The mecha-
nism for its maintenance has been a contentious
issue for more than a century. Coupling to irreg-
ular core motions, atmospheric motions and
earthquakes have all been repeatedly examined
and found inadequate. We now have better evi-
dence of a cause, involving interaction of the
atmosphere and oceans, expressed primarily by
ocean floor pressure variations (Gross, 2000). The
14-month Chandler wobble is superimposed on a
slightly smaller 12-month variation, driven by
seasonal mass re-distribution, and is apparent
as a cyclic variation in the latitudes of observa-
tories, with an amplitude that is a bea t of the
14- and 12-month periods.
The astronomical observations that are the
subject of this chapter have a long history.
The relevance to various solid-Earth problems
emerged more recently. As already mentioned,
the determination of the dynamic ellipticity is
particularly important, but other observations of
interest include the elasticity of the Earth at the
wobble frequency and evidence of coupling of
the core to rotation of the mantle. Lambeck
(1980) gave a comprehensive review of the sev-
eral causes of rotational irregularity discussed in
this chapter and the following one.
7.2 Precession of the equinoxes
The two principal terms in the external gravita-
tional potential of the Earth are given by Eq. (6.13).
The central, r
1
, term is dominant, but the second
term is non-central, that is, it has a latitude
dependence, due to the equatorial bulge. In addi-
tion to the central gravitational force m @V=@rðÞ,
exerted on a mass m at (r,), there is a torque
m @V=@ðÞ, with a corresponding equal and
opposite torque exerted by the mass on the
Earth.Themagnitudeofthetorqueisproportional
to (m/r
3
). For small bodies, such as man-made satel-
lites, the only consequence is a regression of the
nodes of the satellite orbits, that is, a precessional
motion of the orbits about the equatorial plane
(Section 9.2). But the torques exerted on the
Moon and Sun are balanced by the torques exerted
by these bodies on the Earth and cause the preces-
sion of the Earth’s rotational axis. The process is
almost non-dissipative, although the possibility
that there is some precessional dissipation in the
core is considered in Section 24.7, in connection
with the power of the geomagnetic dynamo.
7.2 PRECESSION OF THE EQUINOXES 91
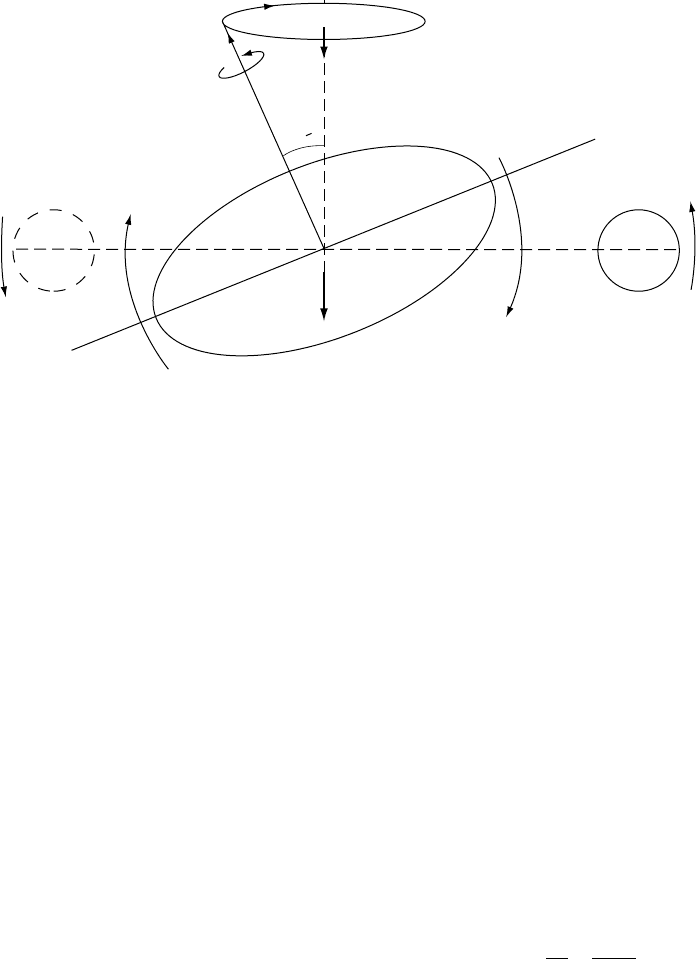
//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C07.3D
–
92
– [90–101] 13.3.2008 10:36AM
The cause of the precessional torque is illus-
trated in Fig. 7.1. The Moon and Sun pull the
equatorial bulge towards alignment with them-
selves. The solar torque is a maximum at the
solstices, when the Sun is 23.58 degrees from
the equatorial plane, and it vanishes at the equi-
noxes, when the Sun is directly above the equa-
tor. But the sense of the torque is the same at
both solstices, so that, although it occurs in semi-
annual pulses, it has a cumulative effect.
Similarly, the lunar torque occurs in semi-
monthly pulses and its average effect is added
to that of the Sun. The lunar contribution is
slightly more than twice the solar one, because
(m/r
3
) is larger for the Moon.
Coupled with the precession are oscillatory
motions of the axis towards and away from the
pole of the ecliptic, that is, in a direction perpen-
dicular to the precessional motion. They are
referred to as nutations (‘nodding’). Semi-annual
and semi-monthly nutations arise from compo-
nents of the solar and lunar torques perpen-
dicular to the precessional component. These
nutational torque components are zero at the
solar and lunar solstices, when the torques are
purely precessional, and at the equinoxes, when
the torques vanish because the Sun or Moon are
in the equatorial plane. A larger amplitude nuta-
tion (9.21 arcsec) of 18.6 year period arises from
the coupling of the Earth to the precession of the
pole of the lunar orbit about the pole of the
ecliptic (Earth’s orbital plane). The consequent
variation in the inclination of the lunar orbit to
the equator causes the Earth’s nutation with the
same period.
To examine quantitatively the precessional
torque on the Earth, consider the geometry of
Fig. 7.2, with the Sun, mass M
S
, instantaneously
at geocentric latitude and distance R from the
Earth’s centre. The gravitational potential at the
centre of the Sun due to the Earth is given by
Eq. (6.13), so that the torque exerted on the Sun,
and therefore by the Sun on the Earth, is
L ¼ M
S
@V
@
¼
3GM
S
R
3
C AðÞsin cos : (7:4)
This torque acts about an axis in the equatorial
plane normal to the Earth–Sun line, that is, it
tends to pull the bulge into line with the instan-
taneous Earth–Sun axis. We can resolve it into
components L
x
about O x and L
y
about Oy. Then L
x
is the torque component causing the semi-
annual nutation and L
y
is the solar precessional
torque.
Pole of
Ecliptic
Axis
Force
Ecliptic
Plane
Sun
(or Moon)
Equator
ω
23
2
°
ω
P
ω
P
1
FIGURE 7.1 Origin of the precessional torque. The gravitational action of the Sun (and Moon) on the alignment
of the Earth’s equatorial bulge exerts a torque that tends to pull the bulge into alignment with the instantaneous
Earth–Sun (or Earth–Moon) axis. The torque vanishes when the Sun (or Moon) crosses the equatorial plane, but
appears with the same sign for both halves of the orbit, causing a net average precessional torque.
92 PRECESSION, WOBBLE AND ROTATIONAL IRREGULARITIES
//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C07.3D
–
93
– [90–101] 13.3.2008 10:36AM
L
y
¼
3GM
S
R
3
C AðÞsin cos sin ; (7:5)
where is the longitude of the Sun, relative to its
longitude at the equinox. Two trigonometric
identities relate , to , ,where is the azimu-
thal angle of the Sun in its orbital plane and is
here the maximum value of (23.58):
sin ¼ sin sin ; (7:6)
tan ¼ tan sin ; (7:7)
so that, in terms of and ,
L
y
¼
3GM
S
R
3
C AðÞsin cos sin
2
: (7:8)
Since gives the Sun’s position in the orbital
plane,
sin
2
¼ 12
=
; (7:9)
and therefore the mean precessional torque,
averaged over a year, is
L
y
¼
3
2
GM
S
R
3
C AðÞsin cos : (7:10)
This annual average torque acts, in the sense of
the arrows in Fig. 7.1, about the axis Oy (Fig. 7.2).
Since Oy is perpendicular to Oz, which is
the axis of the Earth’s angular momentum, C!,
the solar precessional torque causes an angular
rate of change in the orientation of the rotational
axis
O
S
¼ L
y
=C! ¼
3
2
GM
S
R
3
C AðÞ
C!
sin cos
¼
3
2
!
2
S
!
C A
C
sin cos ;
(7:11)
where !
2
S
¼ GM
S
=R
3
is Kepler’s third law
(Eq. (B.23), Appendix B), !
S
being the angular
speed of the Earth–Sun orbital motion.
Still supposing the solar torque to act alone,
as the Earth’s rotational axis moves, the equato-
rial plane moves with it, causing the positions of
the equinoxes (Oy in Fig. 7.2) to move around the
orbit. The axis of the precessional torque moves
with Oy, so that the torque causes the cyclic
precession of the rotational axis about the pole
of the ecliptic, describing a cone of semi-angle .
If the solar torque acted alone, one cycle
of the precession would take a time
PS
¼
2p=!
PS
¼ 2p sin =O
S
, where
!
PS
¼ O
S
= sin ¼
3
2
!
2
S
!
C A
C
cos : (7:12)
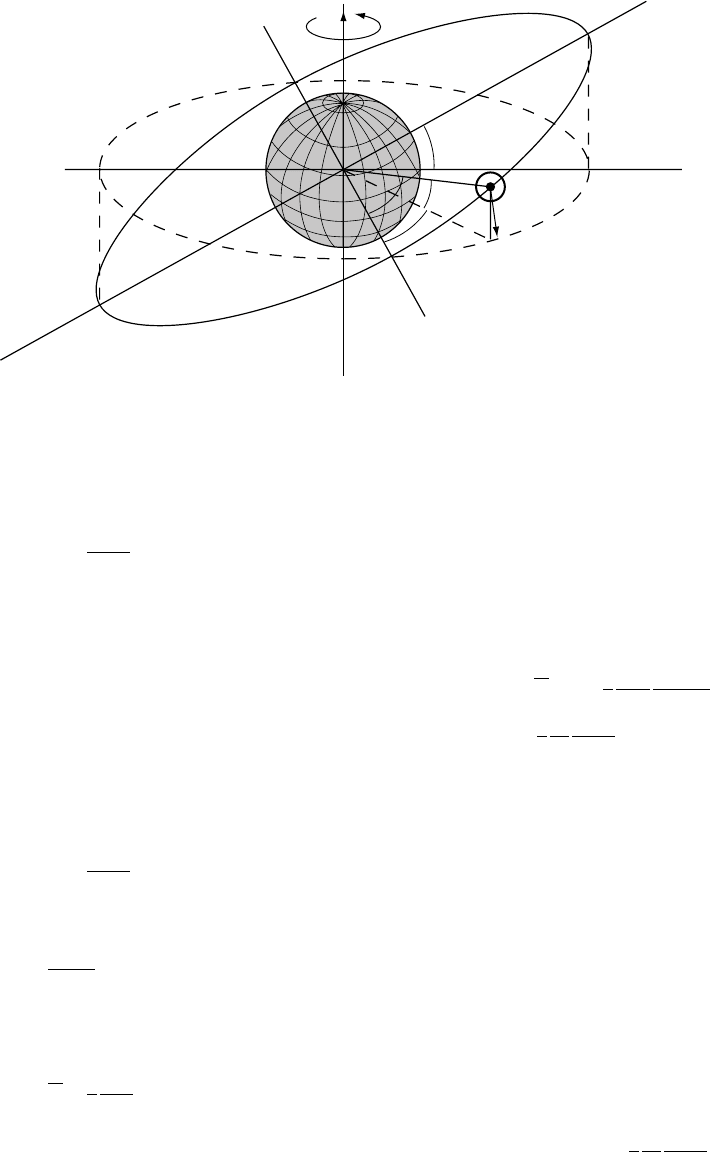
β
φ
θ
α
0
y
x
x'
R
M
s
L
z
ω
FIGURE 7.2 Geometry of the precessional torque. Oxy represents the equatorial plane and z is the rotational axis.
The Sun is at an instantaneous geocentric latitude , on an orbit of radius R in the plane Ox
0
y, inclined at ¼23.58 to
the equatorial plane. The projection of the orbit onto the equatorial plane is shown as the dashed ellipse. For this
purpose we can consider the orbit of the Sun about the Earth as equivalent to the orbit of the Earth about the Sun. A
similar figure applies to the Moon.
7.2 PRECESSION OF THE EQUINOXES 93
//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C07.3D
–
94
– [90–101] 13.3.2008 10:36AM
A similar expression applies to the lunar contri-
bution, !
PL
(except that in substituting Kepler’s
third law it is the mass of the Earth that is dom-
inant for the Earth–Moon system), and the
observed rate of precession, caused by both
solar and lunar torques, is
!
P
¼ !
PS
þ !
PL
¼ 50:3846ð13Þ arcsec=year: (7:13)
Since !
P
is well observed, as are the other quan-
tities in Eq. (7.12) except the moments of inertia,
the precession gives a measure of the dynamical
ellipticity, H ¼(CA)/C (Eq. (7.2)). The fact that this
is less than the geoid ellipticity demonstrates that
the deeper, denser layers of the Earth, notably the
core–mantle boundary, are less elliptical than the
surface (see problem 6.4, Appendix J). Combining
Eqs. (7.2) and (6.14) we obtain the coefficient of the
Earth’s moment of inertia, C/Ma
2
(Eq. (7.3)). This is
an important parameter which Earth models are
constrained to fit (Section 17.6).
Since the precession progressively changes the
orientation of the rotation axis relative to the peri-
gee and apogee of the orbit, there is an associated
climatic cycle. There are also cyclic variations in
the inclination of the ecliptic and the orbital eccen-
tricity. These periodicities in orbital characteristics
have climatic implications first studied in detail by
M. Milankovitch in the early 1940s. Climatic cycles
are observable in the sedimentary record at these
periods (Berger, 1988), and Williams (1991) has
found evidence of Milankovitch cycles as early as
440 million years ago. These observations provide
ausefulcheckontheevolutionofthelunarorbit
(Section 8.4). Implications for climate are consid-
ered in Section 26.4.
7.3 The Chandler wobble
Independently of its gravitational interactions
with external bodies, the Earth undergoes a
free, Eulerian precession, sometimes called the
free nutation in geophysical literature, although
it is not strictly a nutation. To distinguish it from
the forced motions due to interactions with
other bodies, the term wobble, or, in the name
of its discoverer, Chandler wobble, is preferred.
The wobble results from the rotation of the Earth
about an axis that departs slightly from its axis of
symmetry (or greatest moment of inertia). The
total angular momentum remains constant, in
magnitude and direction, but the symmetry axis
follows a circular path about the spin axis, which
remains nearly fixed in absolute orientation.
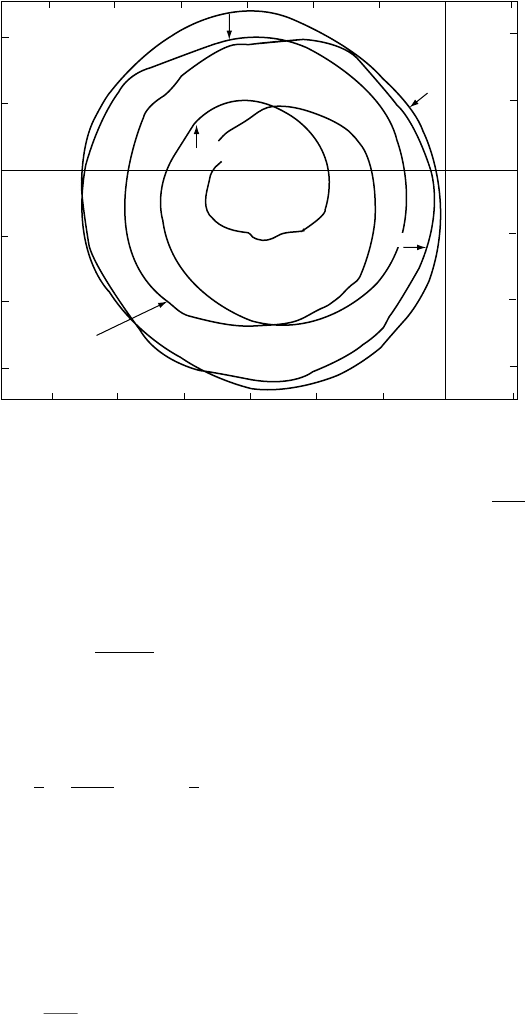
The wobble is apparent as a cyclic variation of
latitude with a period of about 432 days (1.2
years) and variable amplitude averaging about
0.15 arcsec (Vondr
´
ak, 1999). The Chandler wob-
ble is superimposed on a 12-month (seasonal)
latitude variation of 0.1 arcsec amplitude, so
that the two periods are observed to beat, result-
ing in a six-year cycle in the amplitude of the
latitude variation (Fig. 7.3).
The theory of the wobble period is usually
presented in terms of Euler’s equations, but
greatest geophysical interest arises from the
mechanisms of excitation and damping and, for
this purpose, it is convenient to use a derivation
that makes use of wobble energy.
Consider a hypothetical, rigid Earth with
principal moments of inertia C, A, A, where
C > A, rotating with angular velocity ! about an
axis at a very small angle, , to the C axis. The
total rotational energy is the sum of the energies
of the components of rotation about the three
principal axes,
E
T
¼
1
2
Cm
2
3
þ Am
2
1
þ Am
2
2
!
2
; (7:14)
where m
1
, m
2
, and m
3
are the direction cosines of
the rotational axis to the A, A and C axes. Thus
m
2
1
þ m
2
2
¼
2
; (7:15)
where m
2
1
þ m
2
2
þ m
2
3
¼ 1:
The energy of rotation with the same angular
momentum about the C axis, that is, with ¼0
and no wobble, is
E
0
¼
1
2
C!
2
0
: (7:16)
Thus, the kinetic energy of the wobble is the
difference between Eqs. (7.14) and (7.16).
Making use of Eq. (7.15), this is
E
W
¼ E
T
E
0
¼
1
2
C!
2
1
C A
C
2
1
2
C!
2
0
:
(7:17)
94 PRECESSION, WOBBLE AND ROTATIONAL IRREGULARITIES
//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C07.3D
–
95
– [90–101] 13.3.2008 10:37AM
The angular momentum is the vector sum of its
components about the principal axes and is con-
served, so that it is equal to C!
0
(with no wobble),
that is
C!
0
¼ C
2
m
2
3
þ A
2
m
2
1
þ A
2
m
2
2
1=2
!
¼ 1
C
2
A
2
C
2
2
C!:
(7:18)
Substituting for !
0
by Eq. (7.18) in Eq. (7.17), we
have
E
W
¼
1
2
A
C A
C
!
2
2
¼
1
2
AH!
2
2
; (7:19)
where H is the dynamical ellipticity (Eq. (7.2))
obtained from the precession.
Since the excess rotational energy is a func-
tion of the angle , it follows that there is a
gyroscopic torque, L
g
, that tends to turn the
Earth to its lowest energy state ( ¼0):
L
g
¼
dE
W
d
¼AH!
2
: (7:20)
This torque acts on the angular momentum com-
ponent in the equatorial plane, A!, that is, the
component associated with the axial misalign-
ment, and, for the hypothetical rigid Earth,
causes free precessional motion at an angular
frequency
!
W
¼
L
g
A!
¼ H!: (7:21)
This is a prograde motion with a period C/(C A)
days ¼305 days.
A 305-day latitude variation was sought for
many years before the discovery of the 432 day
period by S. C. Chandler in 1891. The difference is
primarily due to the elastic deformation of the
Earth, which partially accommodates the equato-
rial bulge to the instantaneous rotation axis,
reducing the gyroscopic torque. There are also
smaller effects of the oceans and core. Neglecting
the lesser contributions, the solid deformation
reduces the gyroscopic torque, L
g
,bythefactor
305/432 ¼0.7, which means that the bulge is
deflected by an angle 0.3, requiring a shear strain
" ¼ 0:3f 1 10
3
; (7:22)
where f 1/300 is the equatorial flattening.
As mentioned in Section 7.1, for more than a
century a satisfactory explanation for the excita-
tion of the wobble was elusive and the same is
true of its damping. If the excitation is random
then the observed spectrum of the wobble reso-
nance gives a measure of the damping and this is
expressed in terms of the Q of the wobble, for
which there are two alternative (but formally
equivalent) definitions:
–100
–200
0
100
200
300
600 500 400 300 200 100 0
–100
Jan 83
Jan 82
Sept 80
Jan 81
Sept 1985
Jan 85
Y, milliarc sec
X, milliarc sec
Jan 84
FIGURE 7.3 Path of the pole
from late 1980 to late 1985,
approximately one beat period
of the combined 432- (Chandler)
and 365-day (seasonal) motions.
X and Y represent displacements
in the direction of the Greenwich
meridian and 90
o
East. Accuracy
of the observations improved
during this period. By 1985 it was
clear that the irregularities in the
pole path are real. From a record
presented by Carter (1989).
7.3 THE CHANDLER WOBBLE 95
//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C07.3D
–
96
– [90–101] 13.3.2008 10:37AM
Q
W
¼2pE
W
=E
W
; (7:23)
Q
W
¼ !
W
=!
W
: (7:24)
Here DE
W
is the diminution in one wobble
cycle of the energy, E
W
, of an unmaintained
wobble, not a directly observed quantity. !
W
is
the spectral line width (at half power) of the
wobble, so that Q
W
is defined as the sharpness
of the wobble frequency. These definitions have
equivalents in electrical circuit theory, where
the term Q – quality factor – originates. Jeffreys
(1959) presented a mechanical analogue that is
easy to visualize – a circular pendulum and a
group of boys with pea-shooters around it, ran-
domly firing peas at it. The pendulum swings
in response to the impulses and if it is only
lightly damped it may develop a large amplitude,
so that individual impulses have only slight
effects. This is the high Q situation with little
dissipation of energy per cycle and a sharply
defined period of oscillation. If the Q is lowered
by additional damping, the amplitude is
reduced, individual impulses become propor-
tionately more important and the period
becomes more blurred. Application of Eq. (7.24)
to observations gives
Q
W
80; (7:25)
corresponding to decay of an unmaintained
wobble with a time constant 2Q
W
/!
W
30
years, but with a wide range of uncertainty
(30 < Q
W
< 180). An analysis by Vondr
´
ak (1999)
suggests that the wobble is not a simple linear
phenomenon, which the concept of Q assumes,
but that the amplitude and period are related.
However, this may be an artifact of the excitation
mechanism.
The role of mantle anelasticity in damping
the wobble can be examined by considering the
anelastic Q required to give the observed wobble
Q (Eq. (7.25)) with a strain amplitude given by
Eq. (7.22). The volume-averaged rigidity modulus
of the Earth is 124 GPa, so that the elastic
strain energy for a wobble of amplitude is
E
S
ð1=2Þ"
2
V ¼ 6:7 10
25
2
Joules; (7:26)
where V is the volume of the Earth. This com-
pares with
E
W
¼ 7:0 10
26
2
Joules (7:27)
by Eq. (7.19). Thus, for mantle anelasticity to
damp the wobble would require an anelastic Q
S
Q
W
/10 8 and this is so much smaller than the
seismologically observed Q
S
as to be implausible.
Themantlecanmakeonlyaminorcontribution
to Q
W
.
It is important to note that an excitation event
becomes ineffective if it extends over more than
half a wobble period (7 months). Internal torques or
mass displacements that move the symmetry axis
away from the rotation pole at one instant would
move it closer half a period later, when the sym-
metry axis is on the opposite side of the pole. This
leaves coupling of the Earth to the atmosphere and
oceans as the only viable mechanism, as concluded
by Gross (2000). A suggestion that the atmosphere
alone suffices is kept alive by Aoyama and Naito
(2001), although their argument is based on evi-
denceforasharp14-monthpeakinthespectrum
of atmospheric (wind plus pressure) excitation,
which is hard to understand. A reasonably sharp
‘line’ spectrum of excitation for the annual wobble
can be understood as a seasonal effect, so that in
this case the line width is unrelated to damping,
unlike the case of random excitation.
The existence of the forced annual wobble
demonstrates that seasonal movements of the
atmosphere and hydrosphere cause an annual
polar shift of 0.05 arcsec. The 14-month wob-
ble, of average amplitude about 0.15 arcsec, with
dissipation at a rate corresponding to a free
decay time constant of 25 periods, requires exci-
tation by a random source of amplitude 0.15/
ffip
25 ¼0.03 arcsec, a surprisingly large fraction
of the annual excitation. But the wobble Q is not
well observed and these numbers are insecure.
Superimposed on the wobble there is a steady
drift of the pole towards 798 W, at a rate which
Vondr
´
ak estimated to be 0.351†/century (11 cm/
year). It is attributed to asymmetry of the mass
redistribution caused by post-glacial rebound.
The total displacement of the pole in this process
is only of order 1 km. It is not an observation of
polar wander, but it is possible in principle that
true polar wander, driven by mass displacements
in the mantle accompanying changes in convec-
tion pattern, is also occurring.
96 PRECESSION, WOBBLE AND ROTATIONAL IRREGULARITIES
