Справочная энциклопедия дорожника (том I) Строительство и реконструкция автомобильных дорог. Под ред. Васильева А.П

Подождите немного. Документ загружается.

4 4,54 3,18 2,35 1,64

6 3,36 2,57 2,01 1,48

8 3,00 2,37 1,90 1,41

10 2,82 2,26 1,83 1,38

12 2,72 2,20 1,80 1,36

14 2,65 2,16 1,77 1,35

16 2,60 2,13 1,75 1,34

18 2,57 2,11 1,74 1,33

20 2,54 2,09 1,73 1,32

26 2,49 2,06 1,71 1,32

30 2,46 2,04 1,70 1,31

40 2,42 2,02 1,68 1,30

60 2,39 2,00 1,67 1,30

I-II III-IV V -

Значение t при двустороннем ограничении параметра для категории дороги

36.3. Методическая основа оценки качества в дорожном строительстве

Одним из недостатков традиционных методов контроля качества является отсутствие единого критерия

оценки качества СНиП 3.06.03-85. В описываемой методике таким единым критерием является показатель

дефектности. Он выражает главную цель контроля - определяет размер брака в продукции. Данный критерий

широко используется в других отраслях, а также в зарубежных странах.

Определить этот критерий для любого параметра дорожной одежды легко по расчетной номограмме (рис.

36.4).

Однако при балльной оценке качества возникает вопрос о проценте брака, соответствующем той или иной

оценке. Эта задача сугубо технико-экономическая, однако величина показателя дефектности может

пересматриваться при изменении требований к дорогам или условий ее строительства, что вносит

определенную гибкость в указанный критерий.

В первом приближении предлагается использовать балльную оценку качества выполнения отдельного

параметра в зависимости от показателя дефектности по данному параметру, которая применяется в

промышленно-гражданском строительстве. Указанная зависимость представлена в табл. 36.7 п. 1.

Т а б л и ц а 3 6 . 7

Балльная оценка качества работ

№ п/п Показатели

Оценка качества

отлично хорошо удовлетворительно

1. Показатель дефектности 0,000-0,050 0,051-0,100 0,101-0,180

2. Комплексный показатель Р 5,00-4,51 4,50-3,51 3,50-3,00

3. Комплексный показатель Р

ад

5,00-4,51 4,50-3,76 3,75-3,00

Предлагаемая балльная оценка является достаточно жесткой, но вполне выполнимой в современных

производственных условиях. Так, оценка качества строительства дорог по предложенной методике в 11

областях Российской Федерации в 16 % дала отличные результаты, в 35 % - хорошие, что в целом

соответствует сложившемуся в дорожном строительстве уровню качества.

При балльной оценке конструктивных элементов дороги возникает вопрос о совместимости различных

оценок по отдельным параметрам. Так, при оценке качества слоя земляного полотна наибольшую значимость

(важность) имеет его плотность, тогда как геометрические параметры слоя являются менее значительными.

Данное обстоятельство учитывается в СНиП 3.06.03-85 (приложение 2: «Оценка качества строительно-

монтажных работ при строительстве автомобильных дорог»).

Согласно этому документу, выводя общую оценку по каждому слою или элементу дорожной конструкции,

балльную оценку отдельных параметров необходимо приводить к единому комплексному показателю. Из

литературы известно несколько способов нахождения комплексных показателей, но общепринятым в дорожном

строительстве является осреднение балльных оценок с учетом каждого элемента или параметра по формуле







где (36.17)

Р - количественный показатель качества работ;

- оценка качества устройства i-того конструктивного элемента или параметра;

- коэффициент значимости;

n - количество учитываемых элементов или параметров.

Значение коэффициентов значимости конструктивных элементов дорожных одежд и характерных дорожно-

строительных работ были определены путем экспертного опроса и статистической обработки этих данных,

проведенных в среде научных работников и опытных работников производства.

Вместе с тем, анализ данного положения привел к следующему выводу: введение коэффициентов

значимости по каждому контролируемому параметру при всей их обоснованности, существенно загромождает

подсчет комплексных показателей. Это в свою очередь приводит к некорректному отношению к данному

расчету со стороны лиц, занимающихся контролем, что безусловно сказывается на точности самой оценки.

Учитывая, что коэффициенты значимости собственно наиболее дорогих конструктивных элементов

дорожной одежды мало отличаются (находятся в пределах 0,9-1,0), комплексные показатели качества

отдельных видов работ, слоев и конструктивных элементов можно рассчитывать как среднее арифметическое

от балльных оценок соответствующих параметров, то есть по формуле





(36.18)

При этом сопоставительный расчет по формулам (36.17) и (36.18) показал, что точность расчета оценки во

втором случае снижается очень незначительно, тогда как объем расчетов уменьшается существенно.

В обоих случаях оценку качества в зависимости от значения комплексного показателя качества

устанавливают по табл. 36.7 п. 2.

В расчетах формулу (36.18) можно заменять на формулу

345

NNN





где (36.19)

, N

- количество видов работ или параметров, получивших оценки соответственно 5, 4 и 3.

При приемке и оценке качества законченного конструктивного элемента дороги приходится иметь дело в

основном с многослойными конструкциями (основания, покрытия), отдельные слои которых были оценены

ранее на стадии приемки скрытых работ. В этом случае оценку качества устройства многослойных оснований и

покрытий устанавливают по значению комплексного показателя качества, который рассчитывается по формуле

...

2211

CCC

SCSCSC





где (36.20)

, С

,...,С

- сметная стоимость устройства каждого слоя многослойных оснований и покрытий;

, S

,..., S

- оценка качества устройства каждого слоя в баллах;

n - количество слоев.

При этом оценку качества в баллах определяют из табл. 36.7 п. 2.

Среднюю оценку качества устройства оснований или покрытий, состоящих из отдельных участков,

построенных в разное время или в разных местах устанавливают по значению комплексного показателя

качества, рассчитываемого по формуле

345

LLL





где (36.21)

, L

- протяженность принятых участков оснований или покрытий, получивших соответственно оценки

«отлично», «хорошо», «удовлетворительно».

При этом оценку качества в баллах определяют также из табл. 36.7 п. 2.

Оценку качества законченной строительством автомобильной дороги или ее участка устанавливают по

значению комплексного показателя качества, который рассчитывается по формуле

7654321

77665544332211

ЭАД

SSSSSSS

P 







где (36.22)

, S

- соответственно средняя оценка качества в баллах подготовительных работ, устройства

земляного полотна, основания дорожной одежды, покрытия дорожной одежды, искусственных сооружений,

обстановки дороги, зданий и сооружений, входящих в комплекс автомобильной дороги;

, α

, - соответствующие коэффициенты значимости, определенные в табл. 36.8;

- показатель эстетичности (его значение устанавливается приемочной комиссией в зависимости от

качества отделочных работ и внешнего вида дороги в интервале от 0,1 до 0,3).

Зависимость оценки от значения Р

АД

в этом случае устанавливается из табл. 36.7 п. 3.

Виды работ, конструктивные элементы и коэффициенты значимости, используемые при оценке качества

работ по законченной строительством автомобильной дороге (участка), представлены в табл. 36.8.

Т а б л и ц а 3 6 . 8

Виды работ и конструктивные элементы Коэффициент значимости

Подготовительные работы 0,5

Земляное полотно 1,0

Основания дорожных одежд 0,9

Покрытия дорожных одежд 1,0

Искусственные сооружения 0,9

Обстановка дороги 0,7

Здания и сооружения, входящие в комплекс дороги 0,6

Параметры по каждому конструктивному элементу и виду работ, используемые при оценке качества

строительно-монтажных работ при строительстве автомобильных дорог, и условия их оценки представлены в

табл. 36.12, размещенной в конце настоящей главы.

При наличии в составе принимаемого участка автомобильной дороги нескольких искусственных

сооружений или зданий и сооружений, входящих в комплекс автомобильной дороги, среднюю оценку

соответственно по группе однотипных сооружений определяют по значению комплексного показателя

качества, рассчитываемого по формуле

...

2211

ср

CCC

SCSCSС





где (39.23)

, C

,...,C

- сметная стоимость строительства или ремонта каждого сооружения;

, S

,...,S

- оценка качества соответствующего сооружения;

m - количество сооружений на принимаемом участке.

При этом оценку качества в баллах определяют по табл. 36.7 п. 3.

36.4. Методика определения объема и точек измерений при статистическом контроле

Как указывалось в разделе 36.1, при традиционных методах контроля необходимо производить большой

объем измерений при четком предписании мест их проведения. Существенным отличием рассматриваемого

способа определения объема контроля является независимость этого объема от охваченной контролем площади

при достаточно высокой достоверности получаемых результатов. Размеры выборки (объема контроля)

обосновываются на основании методов теории вероятностей, для чего используется формула Чебышева,

имеющая после преобразований следующий вид











 





где (36.24)

n - необходимое число испытаний в выборке;

- коэффициент вариации измеряемого параметра;

ρ - показатель точности измерения параметра;

t - нормируемое отклонение, которое определяется по табл. 36.6.

Анализ формулы (36.24) показал, что с увеличением неоднородности параметра (C

) объем контроля резко

возрастает. Это объясняется тем, что для разных категорий дорог должна иметь место разная степень

достоверности контроля, а следовательно и размер выборки, то есть с повышением категории дороги

увеличивается требуемое число испытаний.

Показатель точности измерения определяется по формуле

ср







где (36.25)

∆ - допустимое отклонение среднего значения параметра или абсолютная ошибка метода измерения;

ср

- среднее значение измеряемой величины.

Чем меньше допуски по отклонению, тем больше становится размер выборки. Кроме того, показатель

точности зависит как от метода измерения, так и применяемых приборов, поэтому в каждом конкретном случае

этот показатель желательно устанавливать индивидуально, но, учитывая сложность этой работы, можно

воспользоваться полученными в результате обобщения накопленных данных лабораторного контроля

ориентировочными значениями ρ и С

, представленными в табл. 36.9.

Т а б л и ц а 3 6 . 9

Ориентировочные значения коэффициентов вариации и показателей точности оценки среднего значения

параметров

Наименование показателя Коэффициент вариации С

Показатель точности ρ

Плотность грунта 0,03 0,015

Плотность асфальтобетона 0,03 0,010

Модуль упругости грунта 0,30 0,100

Модуль упругости слоев дорожной одежды 0,25 0,100

Толщина слоев дорожной одежды 0,20 0,080

Ширина слоев 0,10 0,050

Просвет под трехметровой рейкой 0,80 0,200

Прочность при сжатии асфальтобетонных образцов 0,10 0,050

Прочность при сжатии цементогрунтовых образцов 0,15 0,050

Влажность грунта 0,10 0,050

Сцепление и угол внутреннего трения в грунте 0,10 0,050

Температура асфальтобетона 0,18 0,030

Следует отметить, что при переходе на статистические методы контроля необходимо пересмотреть допуски

на отдельные виды работ, что потребует значительных по объему исследований. В первом приближении

возможно оставить существующие допуски по СНиП 3.06.03-85, несколько их преобразуя. Для примера

рассмотрим установление допусков по толщине слоя. Как известно, современные нормы допускают отклонение

толщины на ±10 %. Следовательно, при переходе на статистический метод контроля нужно поставить

двухстороннее ограничение: слева - [X] = 0,9 Х

ср

, справа - [X] = 1,1 X

ср

. При измерении ровности СНиП 3.06.03-

85 ставит ограничение, например, для асфальтобетона 5 мм, причем дополнительно оговариваются два условия:

просветов более 5 мм должно быть не более 5 % всех измерений и максимальный просвет не должен

превосходить двойной величины допускаемого просвета, то есть 10 мм. Переходя на статистические

ограничения возможно записать их в следующем виде. Допустимой принимается ровность, оцениваемая

просветом под рейкой в 5 мм, определяется показатель дефектности для каждого измерения (например, он

оказался равным 0,07) и сравнивается с допустимым выходом по СНиП 3.06.03-85 (0,07 и 0,05, то есть на 2 %

выход больше допустимого). Кроме того, по рис. 36.2 определяется максимальное значение просвета под

рейкой, которое сравнивается с ограничением R

max

 10 мм.

Приведенные примеры показывают порядок использования существующих допусков для статистического

контроля качества.

Однако в дальнейшем необходимо уточнить допуски, так как некоторые из них не могут быть выполнены,

или они не совсем корректны.

Так, опытные данные убедительно говорят, что допуски по толщине слоя не могут быть постоянными, как

это принято сейчас, для всех толщин слоев. Для более тонких слоев необходимо ослабить допуск, для более

толстых наоборот увеличить. Аналогично для толстых слоев материала можно ослабить требования к ровности

нижележащего слоя, но увеличить их для более тонких слоев.

Некоторые нормативные требования могут быть использованы без изменения, так как уже сейчас они имеют

статистические ограничения. К примеру, в СНиП 2.05.02-85 [86] для плотности грунтов установлены допуски

не ниже определенного коэффициента уплотнения, что подразумевает естественный статистический разброс

плотности.

Вторым важным аспектом подготовки контроля является планирование мест проведения измерений.

Согласно положениям теории вероятностей, необходимая достоверность контроля будет достигнута лишь при

случайном их выборе. То есть, при использовании статистических методов намечать точки контроля следует

только произвольным образом, исключая при этом какой-либо порядок.

Для соблюдения принципа случайности можно использовать таблицу случайных чисел (табл. 36.10), с

помощью которой ликвидируется всякая возможность проявления некорректности при назначении мест

проведения испытаний.

Т а б л и ц а 3 6 . 1 0

Случайные числа

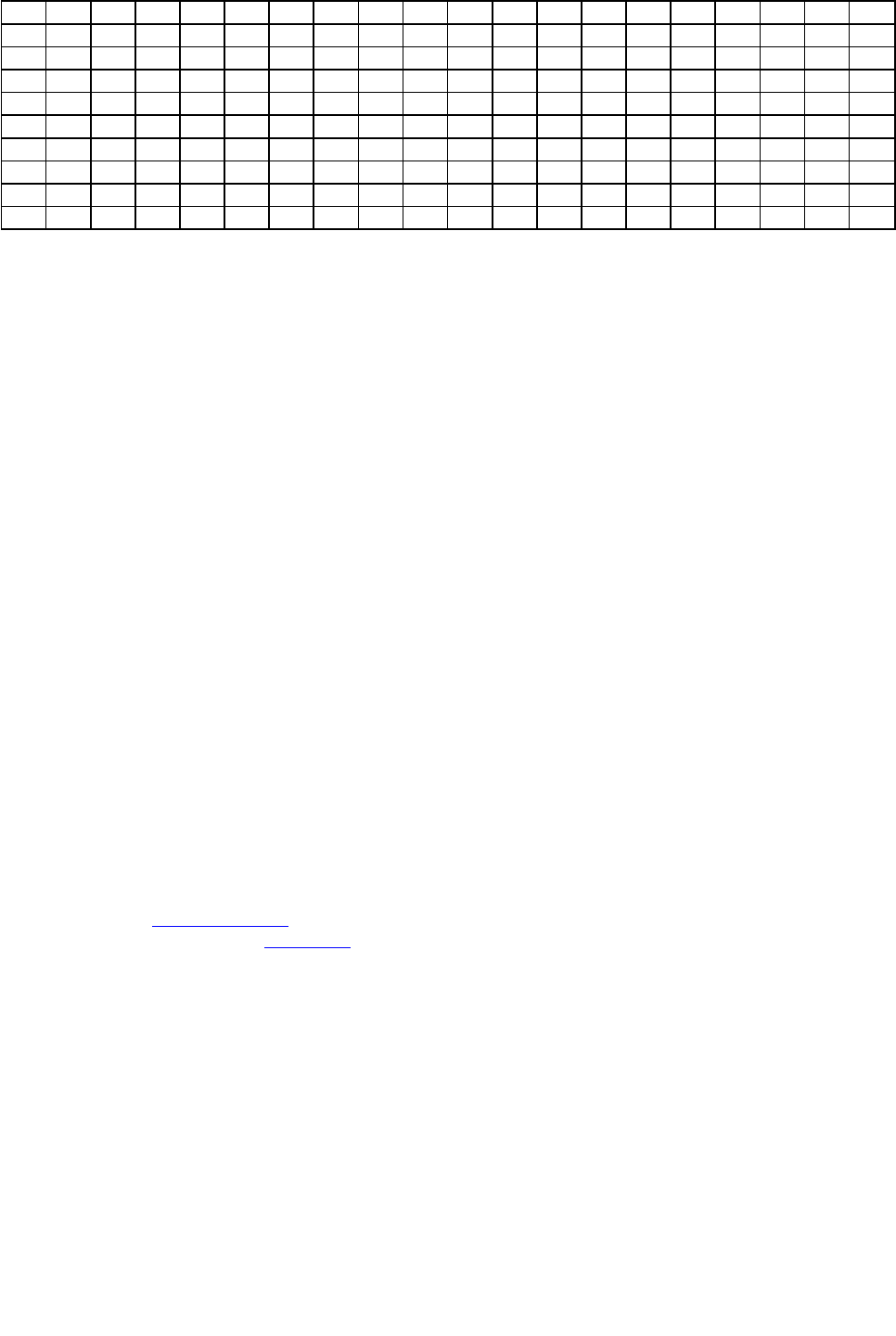
86 51 59 07 95 66 15 56 55 81 23 32 94 37 75 78 02 64 34 56

69 18 60 33 93 42 50 29 92 24 88 95 55 37 58 91 64 11 88 67

41 68 64 21 63 85 18 13 89 76 33 18 17 26 64 53 80 70 06 07

86 52 24 71 71 88 05 98 93 42 67 24 80 90 82 12 31 19 03 60

72 58 79 30 00 89 68 87 84 16 27 55 99 95 28 14 48 05 09 61

52 45 24 24 99 33 34 68 39 35 79 13 09 04 10 45 42 07 77 57

76 77 39 75 26 27 15 66 64 47 25 73 13 75 25 16 28 76 61 81

04 82 58 21 34 80 31 77 51 20 45 80 47 50 01 70 49 21 02 74

87 13 38 47 78 45 86 32 45 20 19 92 50 49 25 07 82 47 60 44

84 75 45 46 17 38 13 26 42 94 15 21 84 92 86 89 57 14 29 03

При выборе мест проведения измерений с помощью табл. 36.10 можно руководствоваться следующим

порядком:

1. Контролируемый участок разбивают на сто зон в зависимости от протяженности таким образом.

При протяженности контролируемого участка до 200-300 м независимо от ширины его разбивают на 20

равных участков по длине, каждый из которых делится на 5 частей в поперечном направлении.

При протяженности контролируемого участка более 300 м:

при ширине дороги до 7 м контролируемый участок разбивают на 100 равных участков по длине;

при ширине дороги от 7 до 14 м контролируемый участок разбивают на 50 равных участков по длине,

каждый из которых делится пополам в поперечном сечении;

при ширине дороги более 14 м контролируемый участок разбивают на 33 равных участка по длине, каждый

из которых делится на три участка в поперечном направлении.

2. Полученные зоны нумеруют двухзначными числами от 00 до 99 (для удобства это может быть выполнено

на листе бумаги в клетку).

3. По таблице случайных чисел (табл. 36.10) произвольно выбирают первую пару чисел, а затем

последовательно по ряду или столбцу берут следующие пары чисел, которые обозначают номера секций для

измерений. Если некоторые выбранные пары (номера секций) совпадают, то их учитывают один раз, выбирая

дополнительно еще одну пару чисел. Общее количество выбранных пар (секций) должно соответствовать

необходимому числу измерений (для удобства выбранные секции отмечаются на подготовленном на бумаге

плане, по которому составляется приблизительный маршрут контроля).

Пример назначения мест измерений с помощью таблицы случайных чисел

Предположим, что рассчитанный по формуле (36.24) объем контроля составляет n = 13. Произвольно по

табл. 36.10 выбираем первую пару цифр, например, 13 (12-й столбец слева, 6-й ряд сверху). Далее по строке

выбираем еще 12 пар: 09, 04, 10, 45, 42, 07, 77, 57, 76, 77, 39, 75. Имеется одно повторение, следовательно,

берем еще одну пару цифр - 26, а одно число 77 исключаем. На плане контроля отмечаем зоны, номера которых

соответствуют выбранным парам. В намеченных зонах будет проводиться контроль качества.

36.5. Обработка результатов статистического контроля и оценка качества

Контроль качества по отдельному параметру осуществляют в любой точке каждой из намеченных зон.

Результаты испытаний, как правило, фиксируют в заранее заготовленных ведомостях контроля, а затем

подвергают статистической обработке. Формы ведомостей практически для всех контролируемых параметров,

предусмотренных СНиП 3.06.03-85, приведены в приложениях «Правил приемки работ при строительстве и

ремонте автомобильных дорог» (ВСН 19-89 / Минавтодор РСФСР. - М.: Транспорт, 1990. - 40 с).

Результаты контроля по каждому в отдельности контролируемому параметру (плотности, ровности, ширине

и т.п.) обрабатывают следующим образом.

Полученные результаты контроля располагают по степени их возрастания в ранжированный ряд (начиная с

меньшего).

Проверяют сомнительные крайние значения ранжированного ряда на принадлежность к ряду, то есть

выясняют не являются ли эти значения случайными выбросами относительно совокупности случайных

результатов.

Для этого по формулам (36.14) рассчитывают значения критерия τ

для минимального и максимального

«сомнительных» значений и затем сравнивают их с критическим значением критерия τ

крит

, которое определяют

по табл. 36.5 в зависимости от числа членов ряда, то есть объема выборки, рассчитанного по формуле (36.24).

Если τ

> τ

крит

, то «сомнительное» значение измеряемого параметра отбрасывают, получают улучшенный ряд.

Как указывалось в разделе 2 допускается более простой способ улучшения ряда - простое отбрасывание

максимального и минимального значений ряда.

После этого определяют среднее арифметическое улучшенного ряда либо по точной формуле (36.12), либо

приближенное, как медиану ряда, то есть выбирается значение, соответствующее среднему члену ряда при

нечетном числе членов ряда или среднему арифметическому двух средних членов ряда при четном числе

членов ряда.

Затем определяют коэффициент вариации либо по точной формуле (36.13), либо упрощенным способом: для

параметров с малыми значениями коэффициента вариации до 0,2 (табл. 36.9) - по формуле (36.15), а для

параметров с большими значениями (табл. 36.9) коэффициента вариации (более 0,2), по формуле (36.16)

определяют значение Z

, а затем, используя рис. 36.2, по значению Z

для данной категории дороги определяют

значение

Далее определяют относительный показатель допуска по формуле (36.11).

По полученным значениям R и

по номограмме (рис. 36.4) с учетом ограничений по контролируемому

параметру определяют значение показателя дефектности или оценку качества в баллах, зависимость между

которыми представлена в табл. 36.7 п. 1.

Если оценка качества по данному параметру оказалась «неудовлетворительно» (показатель дефектности

больше 0,180), проконтролированный участок делят на три равных по длине части, которые подвергаются

аналогичному контролю. При этом учитываются результаты измерений ранее проконтролированных точек,

оказавшихся в границах новых участков. Такое деление участков, получивших неудовлетворительную оценку,

производится до тех пор, пока не будет локализован участок неудовлетворительного качества, подлежащий

переделке или исправлению.

Итак, получив балльные оценки качества выполнения работ по каждому параметру, приступают к оценке

качества отдельных слоев конструктивных элементов дорожной одежды, участков дороги и, в итоге, дороги в

целом, в соответствии с методикой, изложенной в разделе 36.3. Разумеется, контроль и оценка производятся на

всех этапах сдачи и приемки работ: при сдаче и приемке выполненных работ от бригады к бригаде, при

приемке скрытых работ и ответственных конструкций, при сдаче работ заказчику и, наконец, при приемке

объекта в эксплуатацию государственной приемочной комиссией. Таким образом, получаемые на каждом этапе

оценки фиксируются в соответствующих документах, а затем используются в расчетах оценок последующих

этапов приемки. Безусловно эти оценки могут проверяться комиссиями на любом этапе.

36.6. Настройка технологических процессов на стадии подготовки и в процессе строительства

Как было отмечено в разделе 36.1 важным фактором в организации контроля является его специализация.

Опыт использования статистических методов контроля за рубежом указывает на целесообразность разделения

операционного контроля на два этапа: настройку технологического процесса и текущий контроль.

Соответственно изменяется цель контроля. Так, при настройке технологического процесса основной целью

является отработка оптимальных режимов работы механизмов и параметров технологического процесса на

небольшом участке (так называемом эталонном участке). Цель текущего контроля - обеспечение точного

соответствия в процессе производства работ параметров технологического режима, принятых при настройке.

В соответствии с выбранными целями определяется номенклатура контролируемых параметров, степень

обеспечения приборами, частота контроля, уровень контролеров и т.п.

Настройку технологического процесса следует проводить тем же контролерам, которые будут осуществлять

приемочный контроль, то есть контролерам, независимым от строительной организации - сотрудникам

центральной лаборатории. Они должны быть оснащены всеми необходимыми приборами и оборудованием.

Номенклатура измеренных при этом параметров должна соответствовать номенклатуре, установленной

действующими нормативными документами, то есть являться довольно большой. Но частота проведения такого

контроля, разумеется, не очень велика.

Текущий контроль должен производиться постоянно силами непосредственных исполнителей работ, реже

лабораториями строительных организаций. Номенклатура контролируемых параметров при этом должна быть

сведена к необходимому минимуму. Аналогично должны быть до предела упрощены методы контроля и

сокращено использование различных приборов и оборудования.

Такое разделение функций позволяет существенно упростить контроль, сделав его одновременно более

надежным.

Учитывая, что основными операциями технологических процессов являются уплотнение и обеспечение

необходимых геометрических параметров, следует считать целесообразным на стадии текущего контроля

измерять только эти параметры. Такая постановка вопроса позволит строителям обходиться простыми и

надежными приспособлениями: часами, линейкой, рейками, нивелиром и без труда проводить контроль

качества.

При настройке процесса номенклатура измерений должна быть такой, чтобы обеспечить соответствие

получаемого конструктивного слоя требованиям нормативных документов.

Проведенный с учетом высказанных соображений анализ опытных и опубликованных данных позволил

сформулировать номенклатуру основных параметров земляного полотна и дорожной одежды, необходимую

для контроля на этапах настройки и текущего контроля (табл. 36.11).

Т а б л и ц а 3 6 . 1 1

Номенклатура контролируемых параметров при операционном контроле

Наименование контролируемого параметра

Наименование контролируемых параметров при

операционном контроле

настройка текущий контроль

Земляное полотно h, γ, W, n, V, T h, V, T, R

Песчаный слой h, γ, n, V, T h, V, T, R

Щебеночные и гравийные слои h, γ, n, V, T h, V, T, R

Грунтовые и каменные материалы,

укрепленные вяжущими

Q, h, γ, n, V, T Q, h, V, T, R

Асфальтобетон h, γ, t, n, V, T h, t, V, T, R

Цементобетон h, γ, t

, О

,T h, t

, T, R

где

Т - время уплотнения, мин;

h - толщина слоя, м;

Q - содержание компонентов, %;

t - температура материала, °С;

γ - плотность, г/см

;

W - влажность, %;

n - число проходов катка;

V - скорость катка, км/ч;

- температура воздуха, °С;

- осадка конуса, см;

R - ровность, мм.

Для увеличения достоверности результатов контроля при настройке и в процессе проведения работ в этом

случае также целесообразно использовать статистический метод, описанный в предыдущих разделах, в части

планирования объема измерений, методики проведения контроля и статистической обработки его результатов.

При организации работ по настройке технологических процессов необходимо выполнить следующие

работы подготовительного этапа:

выбрать эталонный участок, на котором будет производиться настройка;

подготовить необходимое оборудование и приборы;

определить количество измерений и наметить точки или места проведения контроля на эталонном участке в

процессе настройки;

подготовить необходимые формы производственно-технической документации, в которые будут заноситься

результаты контроля при настройке.

Эталонным участком называют слои земляного полотна, дорожной одежды или всей конструкции, на

которых отрабатывают и тщательно устанавливают параметры технологических режимов производства работ,

обеспечивающих соблюдение требований нормативно-технической и проектной документации.

При настройке используют следующие измерительные средства, приборы и оборудование:

секундомер для контроля времени работы уплотняющих машин и механизмов;

линейку длиной 50 см для контроля толщины слоев земляного полотна, оснований и покрытий;

штангельциркуль для контроля толщины асфальтобетонных покрытий;

термометр ртутный с диапазоном температур от 100° до 200°С для контроля температуры асфальтобетонной

смеси;

термометр ртутный или спиртовой с диапазоном температур от -10° до +50°С для измерения температуры

воздуха;

радиоизотопный гамма-плотномер для контроля плотности грунта в земляном полотне и асфальтобетона в

покрытии;

прибор Ковалева (и при наличии радиоизотопный плотномер-влагомер) - для контроля плотности и

влажности грунта в земляном полотне, а также плотности и содержания битума в асфальтобетоне при

устройстве асфальтобетонного покрытия;

3-х метровая рейка для контроля ровности;

конус для контроля пластичности (жесткости) бетонной смеси;

рулетка на 20 м РЗ-20 для линейного контроля и другие приборы.

Количество и местоположение точек или мест проведения контроля целесообразно устанавливать в

соответствии с рекомендациями раздела 36.4.

Процесс настройки представляет собой пробный технологический процесс, смоделированный на эталонном

участке, в результате которого путем подбора переменных параметров и постоянного контроля показателей

назначения (плотности, прочности и т.п.) устанавливают параметры технологического процесса,

обеспечивающие соблюдение требований нормативно-технической и проектной документации относительно

параметров назначения при имеющихся в наличии средств механизации.

Настройку технологических процессов устройства земляного полотна, оснований и покрытий производят в

основном по показателям назначения, характеризующим прочностные свойства указанных конструкций

(прочности, плотности и т.п.). Окончанием настройки служит момент, когда данные показатели достигают

требований нормативно-технической и проектной документации.

Переменными параметрами при настройке являются такие, изменение которых влечет за собой изменение

показателей назначения. К числу таких параметров относятся толщина отсыпаемого (укладываемого) слоя,

время работы уплотняющих машин, скорость их движения, количество проходов по одному следу, температура

смесей и т.п.

Установленные в процессе настройки параметры технологического процесса фиксируются в акте настройки,

который подписывается лицами, производившими настройку, и передается исполнителю работ.

При настройке соблюдается следующий порядок:

на выбранном эталонном участке отсыпается или укладывается слой соответствующего конструктивного

элемента (земляного полотна, основания, покрытия) заданной толщины. В целях ускорения процесса настройки

на эталонном участке можно устроить несколько более мелких участков с разными толщинами слоев.

Например, при устройстве эталонного участка слоя земляного полотна на нем можно устроить три участка с

толщинами отсыпки 20, 25 и 30 см, которые затем одновременно будут уплотняться проходами одних и тех же

уплотняющих машин;

производится уплотнение эталонного участка имеющимся составом уплотняющих машин. При этом

контролируется количество проходов машин по одному следу и фиксируется скорость движения;

сначала через четыре, а затем через каждые два прохода осуществляется контроль показателей назначения

(плотности, прочности и т.п.). При стабилизации значений этих показателей, то есть когда в результате двух

последовательных циклов измерения получаются одинаковые или мало отличающиеся значения

контролируемых параметров, уплотняющая машина заменяется более тяжелой. Если в результате контроля

получено, что значение контролируемого параметра достигло требований СНиП, то процесс уплотнения

прекращают;

полученные числа и скорости проходов, порядок смены уплотняющих машин, а также результаты контроля

фиксируются;

по полученным числам и скоростям проходов рассчитывают время непрерывной работы уплотняющих

машин

 

1000

























рв

где (36.26)

В - ширина уплотняемого эталонного участка, м;

k - число изменений скорости при укатке;

L - длина уплотняемого эталонного участка или длина уплотняемого слоя постоянной толщины, м;

в - ширина уплотняемой полосы, м;

∆ - величина перекрытия, м (для пневмокатков - 0,5 м; для вальцовых катков - 0,25 м);

- время разворота реверса уплотняющей машины, ч (для самоходных катков - 0.01 ч, для прицепных -

0,02-0,09);

V - скорость движения уплотняющих машин, км/ч;

n - число проходов уплотняющей машины по одному следу;

Р - вероятность прохода по одному следу (принимается равной 0,8).

Затем составляют акт настройки технологического процесса.

36.7. Примеры организации и проведения статистического контроля, оценки качества и настройки

технологических процессов

Чтобы глубже уяснить существо метода статистического контроля и оценки качества рассмотрим несколько

примеров, иллюстрирующих всю последовательность подготовки и проведения контроля, обработки

результатов контроля и оценки качества, настройки технологических процессов.

Пример 1. Необходимо оценить качество уплотнения верхнего слоя земляного полотна на участке 300 м

строящейся дороги III технической категории.

Сначала определяют необходимый объем контроля. Для этого используют формулу (36.24) и табл. 36.6 и

36.9. Принимают ориентировочно n = 10, тогда для дороги III технической категории при одностороннем

ограничении (ограничивают только минимальные значения плотности) по табл. 36.6 получают t = 1,83. По табл.

36.9 для плотности грунта С

= 0,3; ρ = 0,015. Эти значения t, C

и ρ подставляют в формулу (36.24)

.4,13

015,0

3,083,1





































Полученное значение n = 13,4 не соответствует принятому n = 10, поэтому принимают новое целое значение

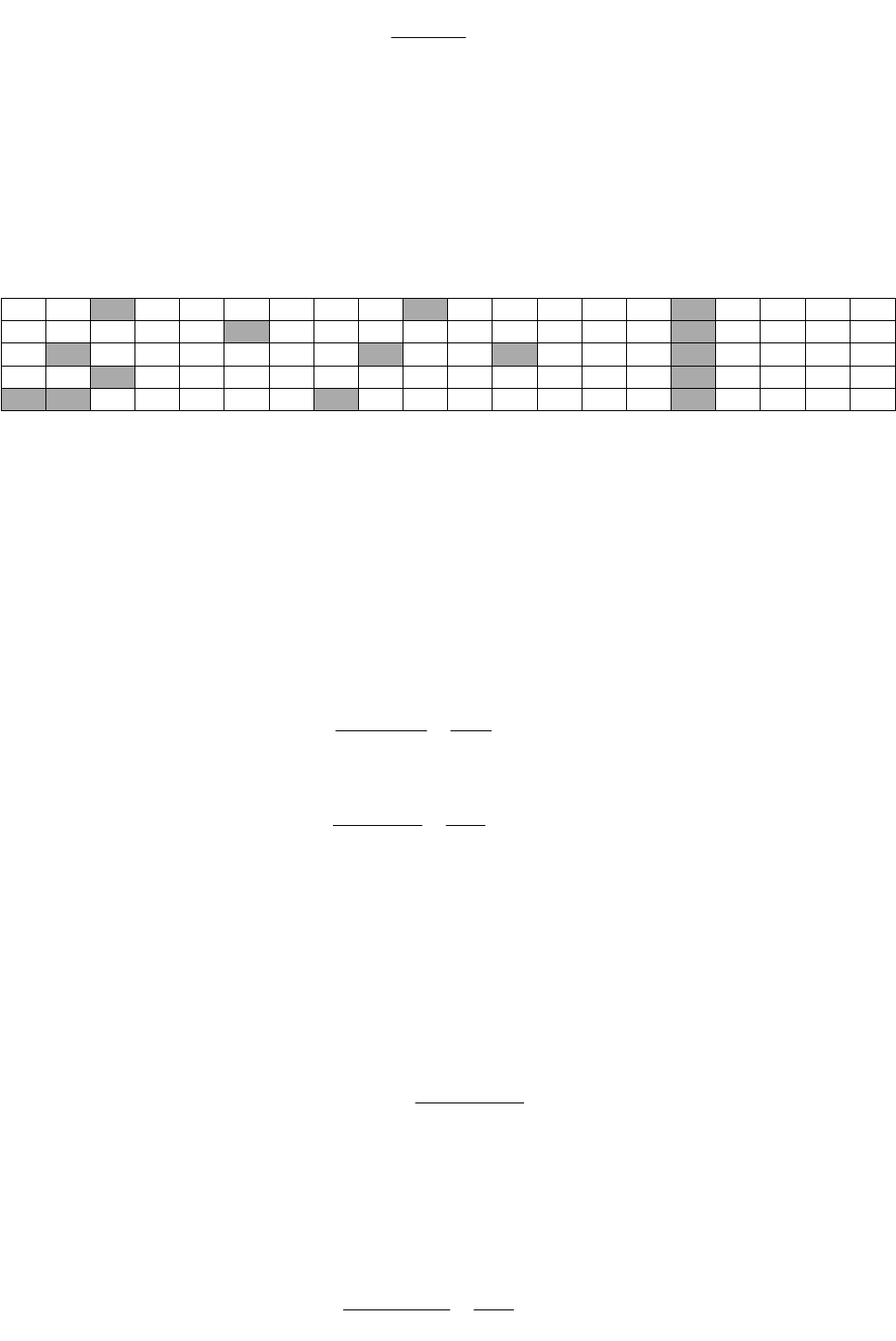
n, ближайшее к полученному - п = 13. По табл. 36.6 определяют новое значение t = 1,78 и подставляют его в

формулу (36.24):

.7,12

015,0

3,078,1

















n

Окончательно принимают п = 13, то есть чтобы оценить качество уплотнения с достаточной достоверностью

необходимо провести 13 измерений в разных точках контролируемого участка.

Согласно примеру, приведенному в конце раздела 4 намечают точки контроля, выбирают по таблице

случайных чисел (табл. 36.10) следующие пары цифр 13, 09, 04, 10, 45, 42, 07, 77, 57, 76, 39, 75, 26. В

соответствии с рекомендациями, приведенными в разделе 4, контролируемый участок разбивают на 20 равных

участков по длине, каждый из которых делят на 5 частей в поперечном направлении. Для удобства на листе

бумаги в клетку составляют план контролируемого участка, нумеруют зоны двузначными числами от 00 до 99

и затем отмечают те зоны, номера которых совпали с выбранными по табл. 36.10 парами (рис. 36.5).

00 05 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95

01 06 11 16 21 26 31 36 41 46 51 56 61 66 71 76 81 86 91 96

02 07 12 17 22 27 32 37 42 47 52 57 62 67 72 77 82 87 92 97

03 08 13 18 23 28 33 38 43 48 53 58 63 68 73 78 83 88 93 98

04 09 14 19 24 29 34 39 44 49 54 59 64 69 74 79 84 89 94 99

Рис. 36.5. Пример составления плана контроля

В любой точке каждой намеченной зоны осуществляется контроль плотности. В результате контроля

получены следующие значения плотностей: 1,88; 1,82; 1,84; 1,90; 1,85; 1,88; 1,87; 1,93; 1,83; 1,80; 1,88; 1,89; 1,89

г/см

Полученные результаты контроля расставляют по возрастающим значениям (в ранжированный ряд): 1,80;

1,82; 1,83; 1,84; 1,85; 1,87; 1,88; 1,88; 1,88; 1,89; 1,89; 1,90; 1,93 г/см

Улучшить ряд можно двумя способами. По упрощенному способу отбрасывают минимальное и

максимальное значения ряда и получают улучшенный ряд: 1,82; 1,83; 1,84; 1,85; 1,87; 1,88; 1,88; 1,88; 1,89; 1,89;

190 г/см

2 способ.

Согласно второму способу проверяют крайние члены на принадлежность ряду по формулам (36.14). По

табл. 36.5 для n = 13 определяют τ

крит

= 0,411

;411,02,0

1,0

02,0

80,190,1

80,182,1

min









.411,027,0

11,0

03,0

82,193,1

90,193,1

max









Таким образом, крайние члены принадлежат имеющемуся ряду и их не следует отбрасывать. Но в

дальнейших расчетах будем использовать улучшенный ряд, полученный первым способом.

Затем определяют среднее арифметическое улучшенного ряда приближенно как медиану ряда, то есть берут

средний член улучшенного ряда (6-й член). Таким образом Х

ср

= 1,82 г/см

, X

ср

можно определить по точной

формуле (36.12).

Потом определяют коэффициент вариации приближенным способом. Из табл. 36.10 видно, что плотность

грунта является параметром, обладающим малым коэффициентом вариации 0,03, значительно меньшим 0,2.

Следовательно используем формулу (36.15)

minmax

ср







По табл. 36.6 для числа членов улучшенного ряда n' = 11, дороги III технической категории, при

одностороннем ограничении параметра (так как по плотности ограничиваются только минимальные значения)

получаем t = 1,82.

Тогда

.0116,0

84,6

08,0

82.188,12

82,190,1









можно определить также по точной формуле (36.13).

Далее определяют относительный показатель допуска. Максимальная плотность для использованного на

данном участке грунта, полученная в приборе стандартного уплотнения составляет 1,89 г/см

. Тогда, при

минимально допустимом коэффициенте уплотнения верхнего слоя земляного полотна (по СНиП 3.06.03-85)

0,98 минимальное допустимое значение плотности составляет [X] = 1,890,98 = 1,85 (г/см

). Следовательно, по

формуле (36.11) получают

 

.98,0

88,1

85,1



ср

По номограмме рис. 36.4 определяют значение показателя дефектности и оценку в баллах. Для этого

выбирают на номограмме кривую, соответствующую R = 0,98. По горизонтальной оси откладывают значение

= 0,0116 и проводят вертикальную прямую до пересечения с выбранной кривой. Из точки пересечения

проводят горизонтальную прямую до пересечения с левой вертикальной осью, по которой определяется

дефектность при ограничении минимальных значений. Таким образом, получают Д = 0,071 (7,1 %), что

соответствует оценке «хорошо».

Итак, статистический контроль плотности верхнего слоя земляного полотна на участке 300 м дороги III

технической категории показал, что уплотнительные работы выполнены на оценку «хорошо». Данная оценка

заносится в акт на скрытые работы.

Пример 2. Необходимо оценить качество земляного полотна при приемке. Согласно СНиП 3.06.03-85 при

контроле качества земляного полотна проверяют: высотные отметки продольного профиля, ширину земляного

полотна, поперечные уклоны, крутизну откосов, поперечные размеры кюветов, нагорных и других канав (по

дну), глубину кюветов при условии обеспечения стока, поперечные размеры дренажей, продольные уклоны

дренажей, ширину насыпных берм, толщину слоя растительного грунта на откосах, плотность грунта

естественного основания и слоев насыпи.

Методом статистического контроля ранее по перечисленным параметрам были получены следующие

оценки: по высотным отметкам продольного профиля 5; по ширине земляного полотна 5; по поперечным

уклонам 4; по крутизне откосов 4; по поперечным размерам кюветов (по дну) 3; по глубине кюветов (сток

обеспечен) 3; по поперечным размерам дренажей 3; по продольным уклонам дренажей 4; по ширине насыпных

берм 4; по толщине слоя растительного грунта на откосах 3; по плотности грунта естественного основания 5; по

плотности грунта в слоях насыпи 4.

По формуле (36.19) определяют значение комплексного показателя качества устройства земляного полотна.

.91,3

453

435435







P

По табл. 36.7 п. 2 по значению Р, равному 3,91 устанавливаем оценку качества устройства земляного

полотна: 3,51 < 3,9 1< 4,5, что соответствует оценке «хорошо».

Пример 3. Необходимо оценить качество двухслойного основания. Нижний слой основания выполнен из

пескоцемента (сметная стоимость 121 ед.), верхний слой - из гравийно-песчаной смеси, укрепленной цементом

(сметная стоимость 145 ед.). При приемке по нижнему слою была выставлена оценка «хорошо», по верхнему -

«отлично».

По формуле (36.20) определяют значение комплексного показателя качества

.54,4

145121

51454121







P

По табл. 36.7 п. 2 по значению Р, устанавливаем оценку качества устройства основания: 4,54 > 4,5, что

соответствует оценке «отлично».

Пример 4. Необходимо установить среднюю оценку качества покрытия, состоящего из трех одинаковых по

конструкции участков, каждый из которых был принят ранее. Участок протяженностью 400 м был принят с

оценкой «отлично», участок протяженностью 200 м - с оценкой «отлично», участок протяженностью 700 м - с

оценкой «хорошо».

По формуле (36.21) рассчитывают

 

.76,4

700200400

70042004005







P