Спекторський І.Я. Дискретна математика
Подождите немного. Документ загружается.

8
4
2
1
12
6
3
4
2
1
15
5
3
1
30
10
6
3
15
5
2
1
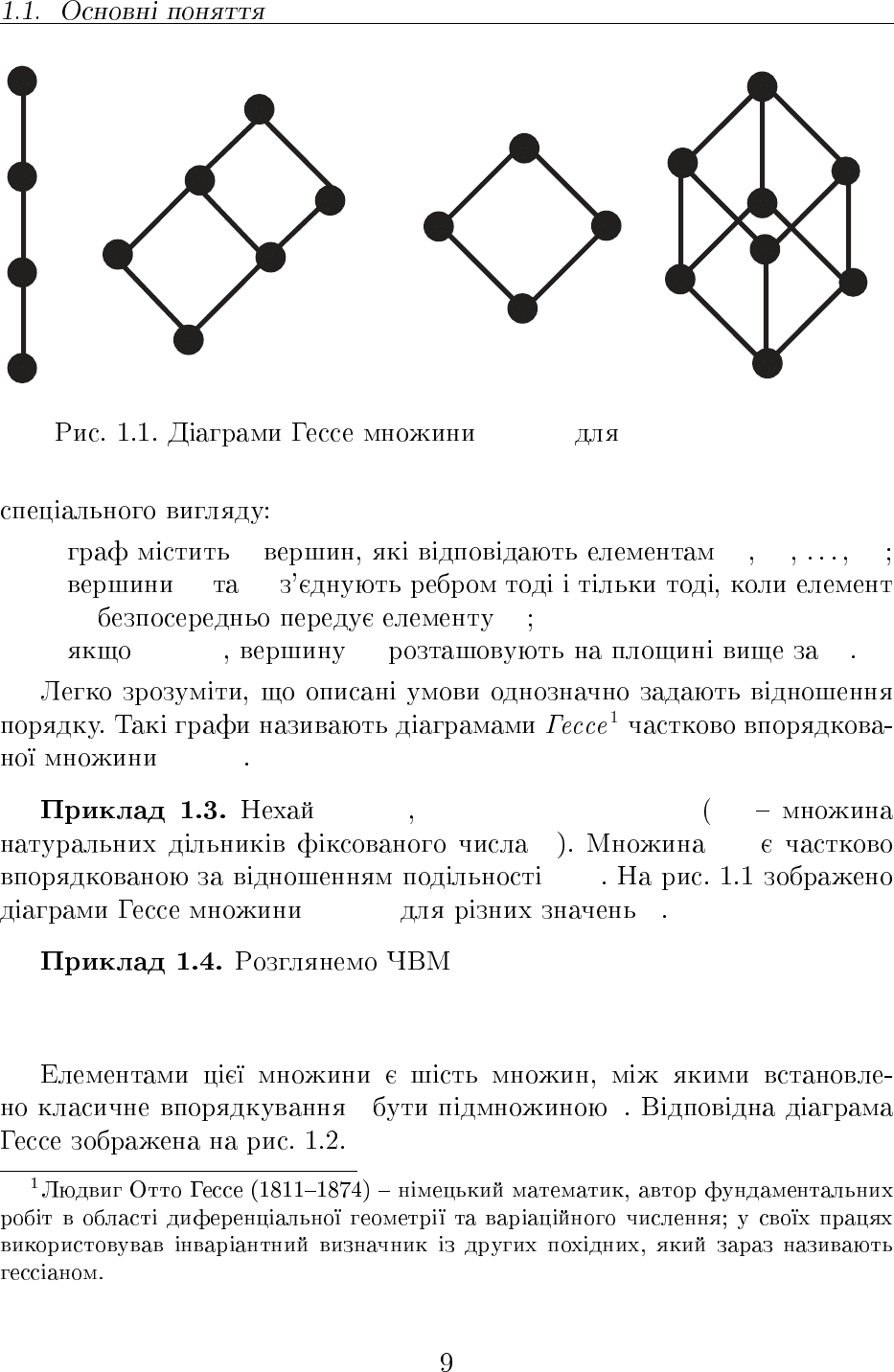
hL
n
, ·
·
·
i n = 8; 12; 15; 30
• n a
1
a
2
a
n
• a
i
a
j
a
i
a
j
• a
i
≺ a
j
a
j
a
i
hA, 4i
n ∈ N L
n
= {k ∈ N : n ·
·
·
k} L
n
n L
n
¿
·
·
·
À
hL
n
, ·
·
·
i n
{{1, 2, 3, 4, 5}, {1, 2, 3, 5}, {1, 2, 4, 5}, {1, 5}, {2, 5}, ∅}.
¿ À
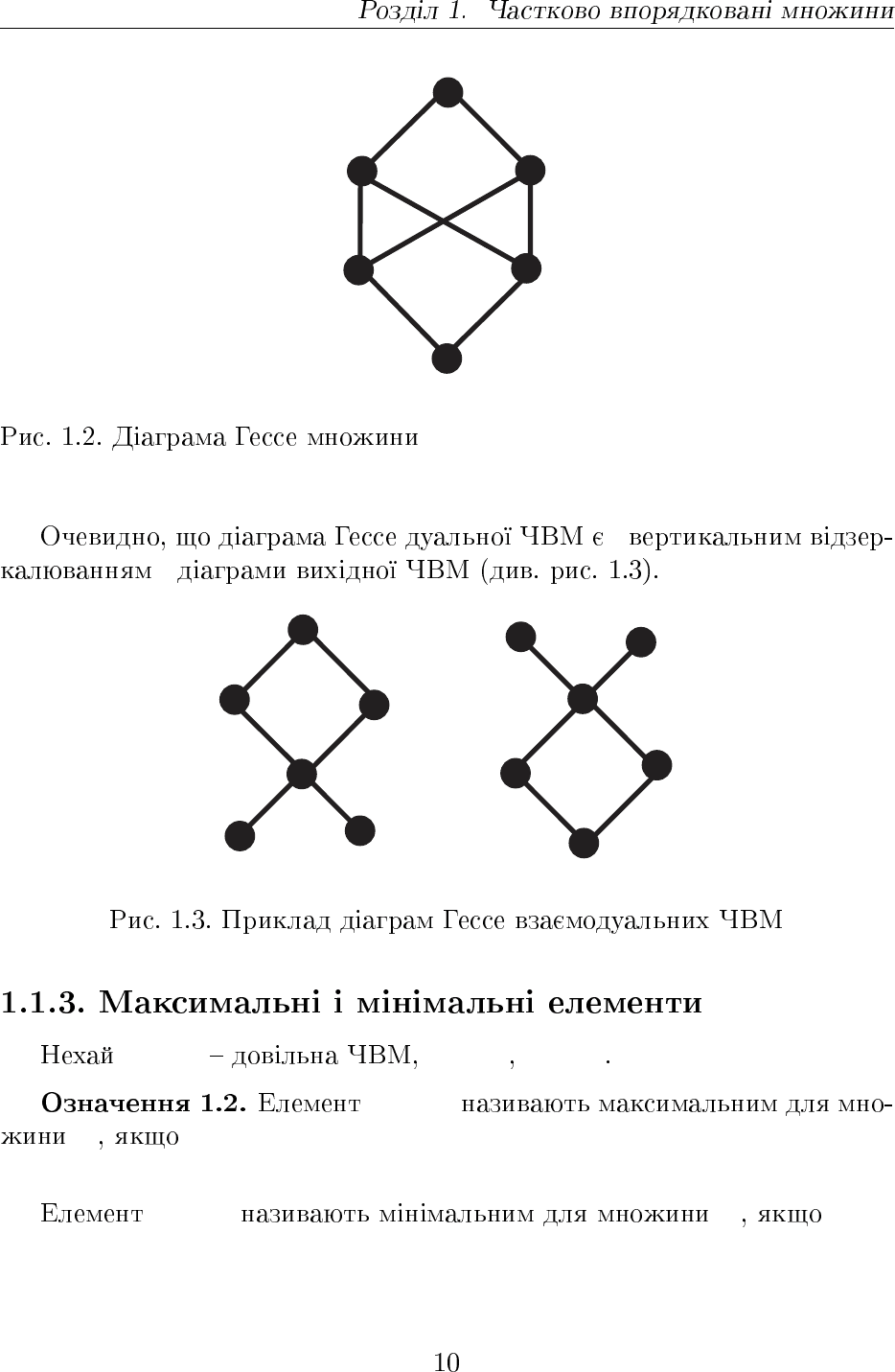
{1,2,3,4,5}
{1,2,3,5}
{1,2,4,5}
{1,5}
{2,5}
Æ
{{1, 2, 3, 4, 5}, {1, 2, 3, 5}, {1, 2, 4, 5},
{1, 5}, {2, 5}, ∅}
¿
À
a
a
c
c
b
b
e
e
f
f
d
d
hA, 4i B ⊂ A B 6= ∅
M ∈ B
B
∀x ∈ B : (x < M) ⇒ (x = M).
m ∈ B B
∀x ∈ B : (x 4 m) ⇒ (x = m).
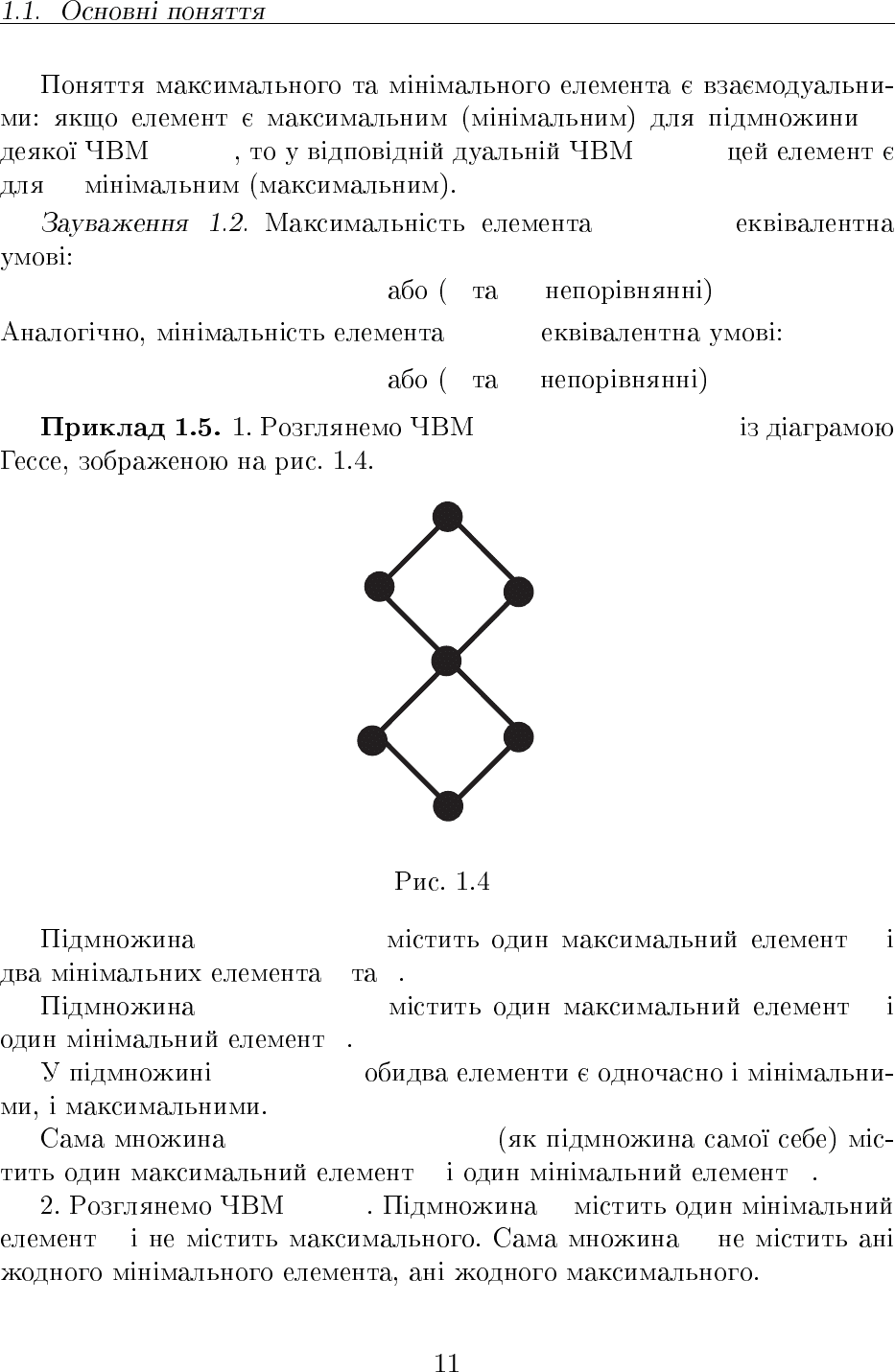
B
hA, 4i hA, <i
B
M ∈ B
∀x ∈ B : (x 4 M) x M .
m ∈ B
∀x ∈ B : (x < m) x m .
A = {a, b, c, d, e, f, g}
a
c
e
f
b
g
d
B
1
= {a, b, c} a
b c
B
2
= {b, d, e} b
e
B
3
= {e, f}
A = {a, b, c, d, e, f, g}
a g
hZ, 6i N
1 Z

B
N hR, 6i
1
hR, >i N 1
hA, 4i B ⊂ A B 6= ∅
M ∈ B
B
∀x ∈ B : (x 4 M).
m ∈ B B
∀x ∈ B : (x < m).
B
hA, 4i hA, <i B
B ⊂ A
B
A
¿ À ¿
À ¿ À ¿ À
B ⊂ A
¿ À ¿ À ¿ À ¿
À
B ⊂ A

B ⊂ A
M
1
∈ B M
2
∈ B
M
1
4 M
2
M
2
4 M
1
M
1
= M
2
¿
4
À ¿
<
À ¿ À
¿ À
B ⊂ A
B ⊂ A
¿ À ¿
À ¿ À ¿ À
A = {a, b, c, d, e, f, g}
B
1
= {a, b, c} a
b c
B
2
= {b, d, e} b
e
B
3
= {e, f}
e f
A = {a, b, c, d, e, f, g} a
g
hA, 4i B ⊂ A B 6= ∅
M ∈ A
B
∀x ∈ B : (x 4 M).

m ∈ A B
∀x ∈ B : (x < m).
B hA, 4i
hA, <i
B
B ⊂ A B
B
B B
A = {a, b, c, d, e, f, g}
B
1
= {a, b, c} a
B
1
a ∈ B
1
d
e f g B
1
B
1
B
1
B
2
= {b, d, e} a b
b ∈ B
2
e g e ∈ B
2
B
3
= {e, f} a b c d
f B
3
A = {a, b, c, d, e, f, g} a
A g
A
hN, 6i
1 ∈ N
{2k : k ∈ N} ∈ N
1 2
B ⊂ A sup B ∈ A
B
B ⊂ A inf B ∈ A
B

M ∈ A
B ⊂ A
M B
f
M ∈ A B ⊂ A M 4
f
M
m ∈ A
B ⊂ A
m B;
em ∈ A B ⊂ A m < em
B ⊂ A
B
M ∈ B ⊂ A M B M
f
M ∈ A
B M ∈ B
M 4
f
M M
B
B ⊂ A
B B
M B
M = sup B M ∈ B
M B M ∈ B
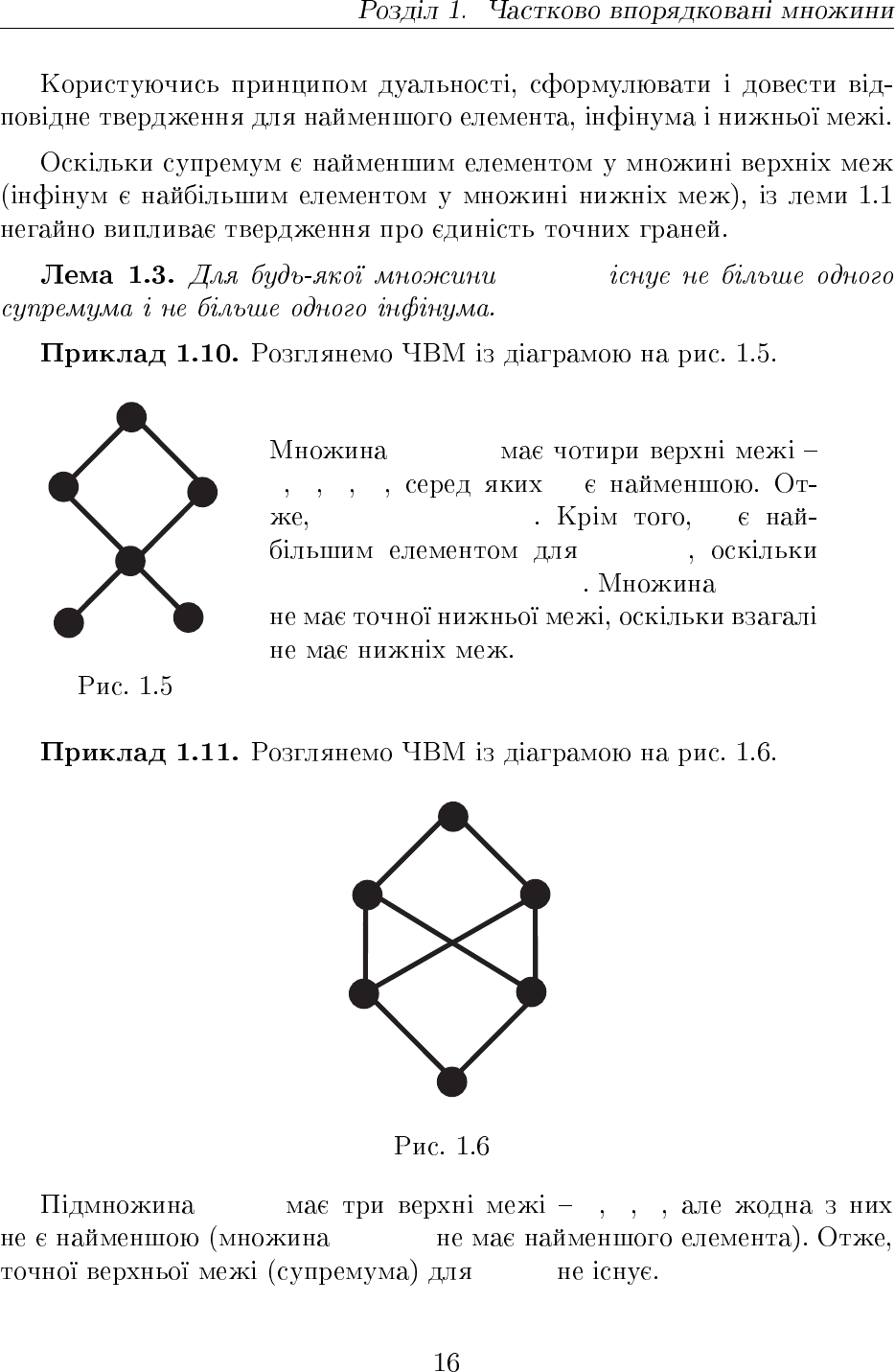
B ⊂ A
a
c
b
e
f
d
{d, e, f}
a b c d d
sup{d, e, f} = d d
{d, e, f}
d = sup{d, e, f} ∈ {d, e, f} {d, e, f}
a
b
c
d
e
f
{d, e} a b c
{a, b, c}
{d, e}

inf{d, e} = f f
{d, e} f {d, e}
f /∈ {d, e} {d, e}
(a 4 b) ⇔ (sup{a, b} = b) ⇔ (inf{a, b} = a)
a, b ∈ A a 4 b b
{a, b} b = sup{a, b} a
{a, b} a = inf{a, b}
a, b ∈ A b = sup{a, b} b {a, b}
a 4 b
a, b ∈ A a = inf{a, b} a {a, b}
a 4 b
A
A sup{a, b}
a, b ∈ A inf{a, b} a, b ∈ A
¿
4
À
sup{a, b} inf{a, b}
a b
B
1
, B
2
⊂ A sup B
1
sup B
2
sup{sup B
1
, sup B
2
} sup(B
1
∪ B
2
)
sup{sup B
1
, sup B
2
} = sup(B
1
∪ B
2
).
inf B
1
inf B
2
inf{inf B
1
, inf B
2
} inf(B
1
∪ B
2
)
inf{inf B
1
, inf B
2
} = inf(B
1
∪ B
2
).

M = sup{sup B
1
, sup B
2
}
B
1
∪ B
2
M < sup B
1
M < x
1
x
1
∈ B
1
M < x
2
x
2
∈ B
2
M < x x ∈ (B
1
∪ B
2
) M
B
1
∪ B
2
f
M ∈ A B
1
∪ B
2
f
M B
1
sup B
1
4
f
M
f
M B
2
sup B
2
4
f
M
f
M {sup B
1
, sup B
2
}
f
M < M = sup{sup B
1
, sup B
2
}
a, b, c ∈ A sup{a, b} sup{b, c}
sup{sup{a, b}, c} sup{a, sup{b, c}} sup{a, b, c}
sup{a, sup{b, c}} = sup{sup{a, b}, c} = sup{a, b, c}.
a, b, c ∈ A inf{a, b} inf{b, c} inf{inf{a, b}, c}
inf{a, inf{b, c}} inf{a, b, c}
inf{a, inf{b, c}} = inf{inf{a, b}, c} = inf{a, b, c}.
B
1
= {d, e} B
2
= {b}
sup B
2
= b sup(B
1
∪B
2
) = sup{b, d, e} = b B
1
= {d, e}
B ⊂ A a ∈ B sup B
inf{a, sup B}
a = inf{a, sup B}.
inf B sup{a, inf B}
a = sup{a, inf B}.
