Спекторський І.Я. Дискретна математика
Подождите немного. Документ загружается.


a
1
, a
2
, . . . , a
n
∈ A
1
a
i
6= a
j
i 6= j
a
1
∨ a
2
∨ · · · ∨ a
n
= a
1
⊕ a
2
⊕ · · · ⊕ a
n
n ≥ 2
n = 2
a
1
∨ a
2
= a
1
⊕ a
2
⊕ a
1
· a
2
= a
1
⊕ a
2
⊕ (a
1
∧ a
2
) = a
1
⊕ a
2
.
n = n
0
≥ 2
n = n
0
+ 1
a
n
0
+1
∧(a
1
∨a
2
∨· · ·∨a
n
0
) = (a
n
0
+1
∧a
1
)∨(a
n
0
+1
∧a
2
)∨· · ·∨(a
n
0
+1
∧a
n
0
) = 0.
a
1
∨a
2
∨· · ·∨a
n
0
∨a
n
0
+1
= (a
1
∨a
2
∨· · ·∨a
n
0
)⊕a
n
0
+1
= a
1
⊕a
2
⊕· · ·⊕a
n
0
⊕a
n
0
+1
,
D
A, ∨, ∧, , 0, 1
E D
B,
ˆ
∨,
ˆ
∧,
b
,
ˆ
0,
ˆ
1
E
f : A → B
a, a
1
, a
2
∈ A
f(a
1
∨ a
2
) = f(a
1
)
ˆ
∨ f(a
2
), f(a
1
∧ a
2
) = f(a
1
)
ˆ
∧ f(a
2
), f(a) =
d
f(a).

f
f(0) =
ˆ
0 f(1) =
ˆ
1
A 2
A
1
A
c ∈ A A
c
= {a ∈ A
1
: a 4 c}
A
c
c ∈ A
A
0
= ∅ c = 1
A A
1
c ∈ A c 6= 0 c =
W
a∈A
c
a
c
˜c =
W
a∈A
c
a ˜c = c
˜c = sup A
c
=
M
a∈A
c
a.
c A
c
˜c = sup A
c
4 c
˜c ≺ c (˜c = c) ⇔ (˜c ⊕ c = 0)
˜c 6= c ˜c ⊕ c 6= 0
a
0
a
0
4 ˜c ⊕ c
a
0
∈ A
c
˜c 4 c
(˜c ⊕ c) ∧ c = (˜c ⊕ c) · c = ˜c · c ⊕ c · c = (˜c ∧ c) ⊕ c = ˜c ⊕ c,
˜c ⊕ c 4 c a
0
4 ˜c ⊕ c 4 c
a
0
∈ A
c
a
0
· (˜c ⊕ c) a
0
4 ˜c ⊕ c
˜c ⊕ c = a
0
a
0
· (˜c ⊕ c) = a
0
· ˜c ⊕ a
0
· c = (a
0
∧ ˜c) ⊕ (a
0
∧ c) = a
0
⊕ a
0
= 0.

a
0
= 0 a
0
˜c ≺ c ˜c = c
A
c
1
= A
c
2
c
1
, c
2
∈ A c
1
= c
2
c
1
=
_
a∈A
c
1
a =
_
a∈A
c
2
a = c
2
.
W
a∈∅
a = 0
c = 0 c ∈ A
c ∈ A c =
W
a∈B
a B ⊂ A
1
B = A
c
a
0
∈ A
1
c ∧ a
0
=
Ã
_
a∈B
a
!
∧ a
0
=
_
a∈B
(a ∧ a
0
).
a a
0
(a ∧ a
0
) =
(
0, a 6= a
0
,
a
0
, a = a
0
,
c ∧ a
0
=
_
a∈B
(a ∧ a
0
) =
(
0, a
0
/∈ B,
a
0
, a
0
∈ B.
inf{c, a
0
} = c ∧ a
0
=
(
0, a
0
/∈ A
c
,
a
0
, a
0
∈ A
c
.
a
0
(a
0
∈ A
c
) ⇔ (a
0
∈ B)
A
c
= B

A A
1
f : A → 2
A
1
f(c) = A
c
, c ∈ A.
f
f
(f(c
1
) = f(c
2
)) ⇔ (A
c
1
= A
c
2
) ⇒ (c
1
= c
2
).
f B ∈ 2
A
1
B ⊂ A
1
c =
W
a∈B
a B = A
c
= f(c)
f
A 2
n
n = card(A
1
) A
A, ∨, ∧, , 0, 1
®
A
1
f : A → 2
A
1
f(c) = A
c
c ∈ A
A, ∨, ∧, , 0, 1
®
2
A
1
, ∪, ∩,
c
, ∅, 2
A
1
®
A
1
A 2
A
1
f : A → 2
A
1
f(c) = A
c
c ∈ A
f
a, a
1
, a
2
∈ A
A
a
1
∧a
2
= A
a
1
∩ A
a
2
, A
a
= (A
a
)
c
.
x ∈ A
a
1
∧a
2
(x ∈ A
a
1
∧a
2
) ⇔ (x 4 a
1
∧a
2
) ⇒
(
x 4 a
1
,
x 4 a
2
⇔
(
x ∈ A
a
1
,
x ∈ A
a
2
⇔ (x ∈ A
a
1
∩A
a
2
),
A
a
1
∧a
2
⊂ A
a
1
∩ A
a
2
x ∈ A
a
1
∩ A
a
2
(x ∈ A
a
1
∩A
a
2
) ⇔
(
x ∈ A
a
1
,
x ∈ A
a
2
⇔
(
x 4 a
1
,
x 4 a
2
⇒ (x 4 a
1
∧a
2
) ⇔ (x ∈ A
a
1
∧a
2
),
A
a
1
∩ A
a
2
⊂ A
a
1
∧a
2
A
a
1
∧a
2
= A
a
1
∩ A
a
2
A
a
= (A
a
)
c
x ∈ A
a
x ∧ (a ∨ a)
x ∧ (a ∨ a) = (x ∧ a) ∨ (x ∧ a) =
(
0, x /∈ A
a
x /∈ A
a
,
x, x ∈ A
a
x ∈ A
a
,
x ∧ (a ∨ a) = x
x a a x
a a
x 4 a∧a = 0 x
a a
(x ∈ A
a
) ⇔ (x /∈ A
a
) ⇔ (x ∈ (A
a
)
c
),
A
a
= (A
a
)
c
1
v
w
b
u
a
c
0
{ , , }abc
{ , }bc
{ }b
{ , }ab
{ }a
{ }c
Æ
{ , }ac
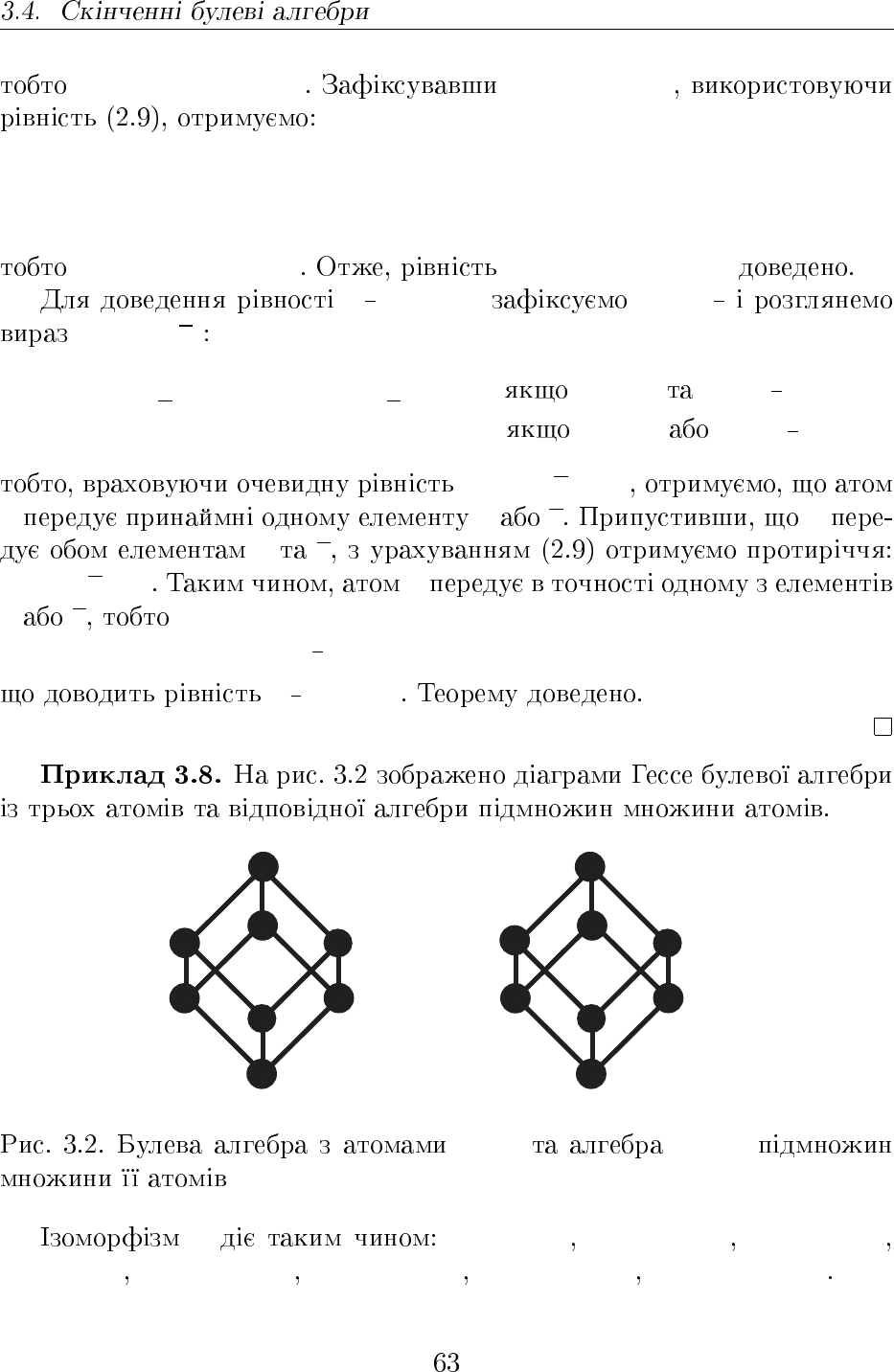
a, b, c 2
{a,b,c}
f f(0) = ∅ f(a) = {a} f(b) = {b}
f(c) = {c} f(u) = {a, b} f(v) = {a, c} f(w) = {b, c} f(1) = {a, b, c}

L
n
n = p
1
p
2
· · · p
m
p
1
p
2
p
m
(L
n
)
1
= {p
1
, p
2
, . . . , p
m
} f : L
n
→ 2
{p
1
,p
2
,...,p
m
}
f(c) = {p
k
(k = 1, 2, . . . , m): c ·
·
·
p
k
},
c ∈ L
n
p
k
k = 1, 2, . . . , m c
2
U
U
2
U
U
A, ∨, ∧, , 0, 1
®
A
a b c
1
x
2,5
A, ∨, ∧, , 0, 1
®
A, ∨, ∧, , 0, 1
®
• 0 1

• A B (A ∨ B) (A ∧ B) A
•
(x∨y) (x
1
∧(a∨ y)) (1∨a)
x ∨ y ∧ z
x → y x ∨ y
x ↔ y (x → y) ∧ (y → x) x ⊕ y
x ↔ y
¿
→
À ¿
↔
À ¿
⊕
À
2
¿
∧
À ¿
∨
À
(x ∨ y) x ∨ y
E
E(x, y, z) x, y, z
E(x, y, z) = (x ∨ y) ∧ z
E(x, y, z) = x ∨ y E(x, y, z) = z
E(x
1
, . . . , x
n
) A
A
×n
A
hS, ∪, ∩,
c
, ∅, Ui E
1
(A
1
, A
2
) = A
1
∪ A
2
E
2
(A
1
, A
2
) = A
1
∩ A
2
E
3
(A
1
, A
2
) = A
1
∩ A
c
2
A
×n
A
A
E
1
(x, y) = x ∨ y E
2
(x, y) = y ∨ (y ∧ x) E
3
(x, y) = x ∨ (x ∧ y)
(x, y) 7→ x ∨ y
A
f : A
×n
→ A
A

x ∧ y (x ∧ y) ∧ z x y
x ∨ y
(x ∧ y) ∧ z x ∧ (y ∧ z)
(x ∧ y) ∧ z x ∧ (y ∧ z) x ∧ y ∧ z
x ∧ y ∧ z x ∧ z ∧ y z ∧ y ∧ x
1 0
E(x
1
, . . . , x
n
) n
x∧ y x, y
x, y, z
E
1
∨ E
2
∨ · · · ∨ E
k
E
1
, E
2
, . . . , E
k
E
1
E
2
E
k

(x ∧ y) ∨ (y ∧ z) ∨ (x ∧ y ∧ z) 2 2 3
x ∧ y 2
x ∨ y 1
1
0
E
1
∨ E
2
= E
1
∧ E
2
E = E
E
1
∧(E
2
∨E
3
) = (E
1
∧E
2
)∨(E
1
∧E
3
)
x∧((x ∨ y) ∧ x ∧ z) = x ∧((x∧ y) ∨(x∧z)) = (x∧x ∧ y)∨(x ∧ x∧z) = x ∧z
x ∨ (y ∧ x ∧ z) = x ∨ (y ∧ (x ∨ z)) = x ∨ (y ∧ x) ∨ (y ∧ z).
x = x ∨ (x ∧ y) = (x ∧ y) ∨ (x ∧ y)

E(x, y) = (x ∧ y) ∨ (x ∧ y)
E(x, y, z) = (x ∧ y ∧ z) ∨ (x ∧ y ∧ z)
E(x) = x
x
x x, y
0
E
x E
x
E = ( E ∧ x) ∨ (E ∧ x).
E(x, y) = (x ∧ y) ∨ x
y
E(x, y) = (x ∧ y) ∨ x = ( x ∧ y) ∨ (x ∧ y) ∨ (x ∧ y).
E(x, y, z) = (x ∧ y) ∨ z
z
