Спекторський І.Я. Дискретна математика
Подождите немного. Документ загружается.


f(
1
, . . . ,
n
) = f(
1
, . . . ,
n
) = c,
c ∈ {0, 1}
g(x) = f(x ⊕
1
, x ⊕
2
, . . . , x ⊕
n
)
g(0) = f(
1
, . . . ,
n
) = c, g(1) = f(
1
, . . . ,
n
) = c,
g(0) = g(1) = c g(x) = c x ∈ {0, 1}
x ⊕
k
1 ≤ k ≤ n
f(x
1
, . . . , x
n
) x x
g(x) = c {f, x}
{0, 1} c
0 1 f /∈ S x
f(x
1
, x
2
) = x
1
∨ x
2
f
∗
(x
1
, x
2
) = x
1
∧ x
2
f
= (0, 1)
g(x) = f(x ⊕ 0, x ⊕ 1) = f(x, x) = x ∨ x = 1.
1 = f(x, x) 0
0 = 1 = f(x, x)
{⊕, ∧, 0, 1} {0, 1}
¿
⊕
À ¿
∧
À
¿
∧
À ¿
·
À
¿
⊕
À ¿
·
À

x ⊕ (y ⊕ z)
(x ⊕ z) ⊕ y x · (y · z) (x · z) · y
x⊕y ⊕z x·y ·z
¿
·
À
¿
⊕
À ¿
·
À
x ⊕ (y · z) x ⊕ y · z
¿
·
À ¿
·
À
a·x·y
axy
n
a ⊕ a
1
x
1
⊕ a
2
x
2
⊕ · · · ⊕ a
n
x
n
⊕ a
1,2
x
1
x
2
⊕ a
1,3
x
1
x
3
⊕ · · · ⊕ a
n−1,n
x
n−1
x
n
⊕
⊕a
1,2,3
x
1
x
2
x
3
⊕ · · · ⊕ a
n−2,n−1,n
x
n−2
x
n−1
x
n
⊕ · · · ⊕ a
1,2,...,n
x
1
x
2
· · · x
n
,
a
j
1
,j
2
,...,j
k
0 ≤ k ≤ n 0 1
n = 0
a 0 1
n = 1, 2, 3 x, y, z
f
(1)
(x) = a ⊕ a
1
x
f
(2)
(x, y) = a ⊕ a
1
x ⊕ a
2
y ⊕ a
1,2
xy
f
(3)
(x, y, z) = a ⊕ a
1
x ⊕ a
2
y ⊕ a
3
z ⊕ a
1,2
xy ⊕ a
1,3
xz ⊕ a
2,3
yz ⊕ a
1,2,3
xyz
¿
⊕
À
x
j
1
x
j
2
· · · x
j
k
a
j
1
,j
2
,...,j
k
1 a
j
1
,j
2
,...,j
k
= 0 x
j
1
x
j
2
· · · x
j
k
a 1
x = 1 ⊕ x
x ∨ y = x ⊕ y ⊕ xy
2

x ↔ y = x ⊕ y = 1 ⊕ x ⊕ y
x → y = x ∨ y = x ∧ y = 1 ⊕ x · (1 ⊕ y) = 1 ⊕ x ⊕ xy
¿
⊕
À ¿
·
À
¿ À
x·x = x
¿ À
x⊕ x = 0
n
n
x
1
, x
2
, . . . , x
n
2
n
x
j
1
x
j
2
· · · x
j
k
0 ≤ k ≤ n
n
2
n
2
2
n
n
n n
f
(n)
f
(n)
¿
⊕
À
1 ⊕ A ⊕ B

f(x, y, z) = x ∨ (y ↔ z)
x ∨ (y ↔ z) = x ∧ y ↔ z = 1 ⊕ x · (y ⊕ z) = 1 ⊕ xy ⊕ xz.
f(x, y) = x ↔ (x ∨ y)
x ↔ (x ∨ y) = x ⊕ (x ⊕ y ⊕ xy) = 1 ⊕ x ⊕ x ⊕ y ⊕ xy = 1 ⊕ y ⊕ xy.
f
(n)
f
(n)
(x
1
, x
2
, . . . , x
n
) = a ⊕ a
1
x
1
⊕ a
2
x
2
⊕ · · · ⊕ a
n
x
n
L
0 1 x x x ⊕ y x ↔ y
1 x y
0
x ∧ y = xy x ∨ y = x ⊕ y ⊕ xy x → y = 1 ⊕ x ⊕ xy
¿ À
xy
L
f /∈ L
x ∧ y ∈ [{f, x, 0}]
f x 0
f
(n)
/∈ L n ≥ 2 0 1
f
(n)
0
x
2 f
2 f

E m 2 ≤ m ≤ n
m m = 2
E x
1
, x
2
, . . . , x
m
f(x
1
, . . . , x
n
) = a ⊕ x
j
1
⊕ · · · ⊕ x
j
k
| {z }
⊕ x
1
x
2
· · · x
m
| {z }
E
⊕
⊕
| {z }
m
g(x, y) = f
(n)
(x, y, y, . . . , y
| {z }
m
, 0, . . . , 0
| {z }
n−m
),
f(x
1
, . . . , x
n
) x x
1
y
x
2
, . . . , x
m
0 x
m+1
, . . . , x
n
E(x
1
, . . . , x
m
)
E(x, y, y, . . . , y) = xy
m
E(x
1
, . . . , x
m
)
x
m+1
, . . . , x
n
g(x, y)
g(x, y) = a ⊕ a
1
x ⊕ a
2
y ⊕ xy,
g(x, y) /∈ L g ∈ [{f, 0}]
f
(n)
0 g
(2)
x ∧ y = xy g(x, y) x 0
,
1
,
2
∈ {0, 1}
g(x ⊕
1
, y ⊕
2
) ⊕ = xy.
g(x⊕
1
, y⊕
2
)⊕ = (a⊕a
1
1
⊕a
2
2
⊕
1 2
⊕ )⊕(a
1
⊕
2
)·x⊕(a
2
⊕
1
)·y⊕xy.

a
1
⊕
2
= 0,
a
2
⊕
1
= 0,
a ⊕ a
1
1
⊕ a
2
2
⊕
1 2
⊕ = 0,
,
1
,
2
1
= a
2
,
2
= a
1
,
= a ⊕ a
1
a
2
,
h(z) = c⊕z
c ∈ {0, 1} h(z) = z c = 0
h(z) = z c = 1 h(z)
xy g(x, y) x
0 x
x ∧ y
f(x
1
, x
2
, x
3
, x
4
) = x
1
⊕ x
3
⊕ x
1
x
3
x
4
⊕ x
2
x
3
x
4
⊕ x
1
x
2
x
3
x
4
0
x
f 0
g(x, y) f 2
E
3 E = x
1
x
3
x
4
E
m
g(x, y)
f(x
1
, x
2
, x
3
, x
4
) x x
1
y x
3
x
4
x
2
E 0
g(x, y) = f(x, y, 0, y) = x ⊕ y ⊕ xyy ⊕ 0 · yy ⊕ x · 0 · yy = x ⊕ y ⊕ xy.

a = 0 a
1
= 1
a
2
= 1 g(x, y) x
1 2
1
= a
2
= 1,
2
= a
1
= 1, = a ⊕ a
1
a
2
= 1,
x ∧ y = g(x ⊕ 1, y ⊕ 1) ⊕ 1 = g(x, y) = x ⊕ y ⊕ x · y.
K ∈ P
2
K
T
0
T
1
M S L
([K] = P
2
) ⇔
K 6⊂ T
0
,
K 6⊂ T
1
,
K 6⊂ M,
K 6⊂ S,
K 6⊂ L.
K ⊂ T
0
T
0
[K] ⊂ [T
0
] = T
0
T
0
6= P
2
x 6= T
0
K 6⊂ T
0
K T
1
M S L
P
2
x /∈ T
1
x /∈ M x ∧ y /∈ S x ∧ y /∈ L
K K 6⊂ T
1
K 6⊂ M K 6⊂ S K 6⊂ L
K 6⊂ T
0
K 6⊂ T
1
K 6⊂ M
K 6⊂ S K 6⊂ L K f
T
0
/∈ T
0
f
T
1
/∈ T
1
f
M
/∈ M f
S
/∈ S f
L
/∈ L f
T
0
f
T
1
f
M
f
S
f
L
K
S L f
S
f
L
x ↓ y = x ∨ y
x ↓ y ∈ K
f
T
0
f
T
1
f
M
f
S
f
L

K x ∧ y x
f
T
0
, f
T
1
, f
M
, f
S
, f
L
∈ K {x ∧ y, x}
0 1 x f
T
0
, f
T
1
, f
M
, f
S
f
T
0
∈ T
1
f
T
1
∈ T
0
f
T
0
f
T
1
f
T
0
f
T
1
0 1
(
f
T
0
/∈ T
0
,
f
T
0
∈ T
1
⇒ 1 ∈ [{f
T
0
}];
(
f
T
1
/∈ T
1
,
f
T
1
∈ T
0
⇒ 0 ∈ [{f
T
1
}].
x
x ∈ [{f
M
, 0, 1}]
f
T
0
/∈ T
1
f
T
1
/∈ T
0
f
T
0
f
T
1
x f
T
0
f
T
1
(
f
T
0
/∈ T
0
,
f
T
0
/∈ T
1
⇒ x ∈ [{f
T
0
}],
(
f
T
1
/∈ T
0
,
f
T
1
/∈ T
1
⇒ x ∈ [{f
T
1
}].
0 1
0, 1 ∈ [{f
S
, x}]
f
T
0
, f
T
1
, f
M
, f
S
0 1 x x ∧ y
x ∧ y ∈ [{f
L
, x, 0}]
K ⊂ P
2
K
1
⊂ K
{→, ⊕}
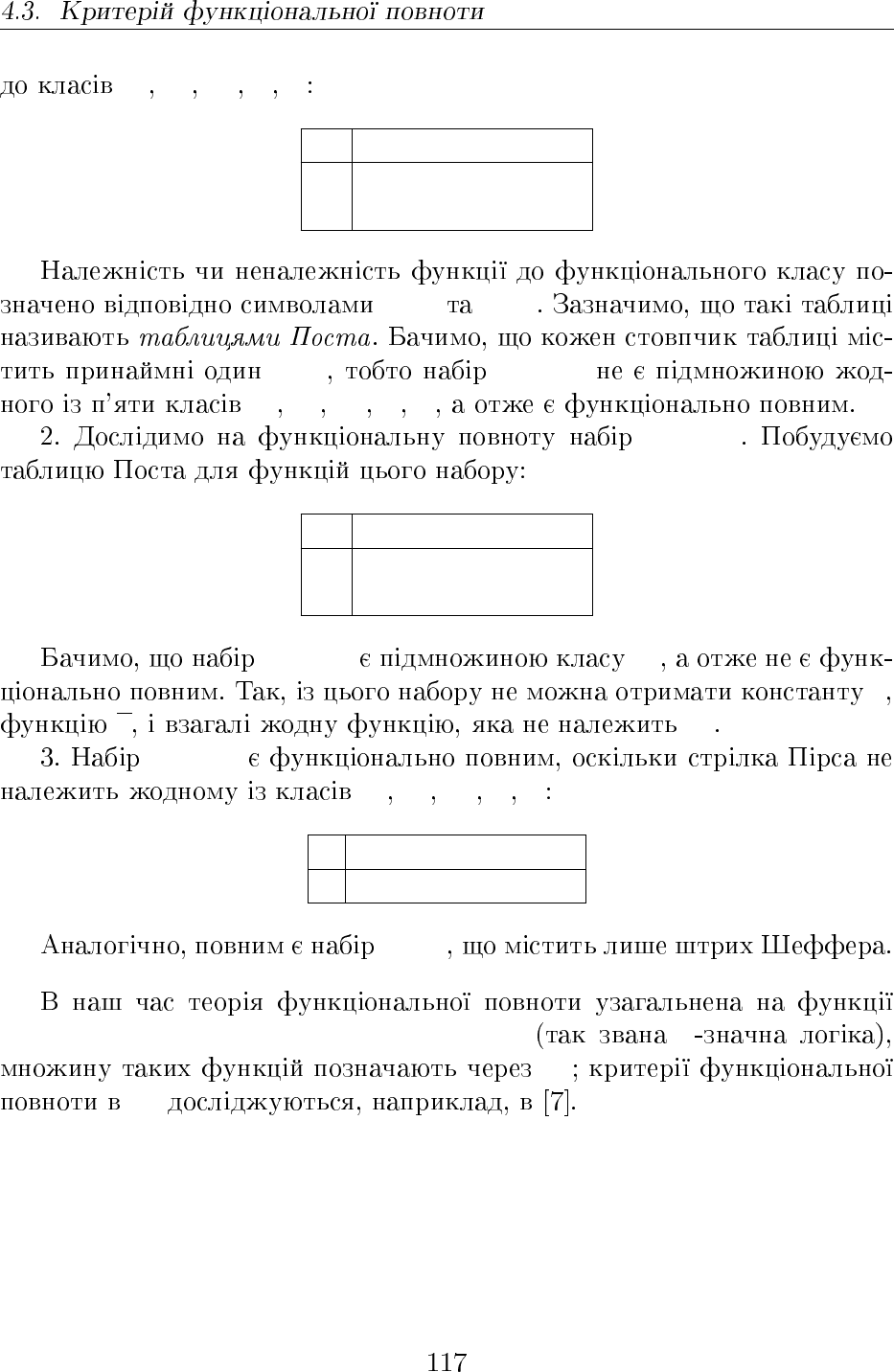
T
0
T
1
M S L
T
0
T
1
M S L
→ − + − − −
⊕ + − − − +
¿
+
À ¿
−
À
¿
−
À
{→, ⊕}
T
0
T
1
M S L
{→, ↔}
T
0
T
1
M S L
→ − + − − −
↔ − + − − +
{↔, ⊕} T
1
0
x T
1
{x ↓ y}
T
0
T
1
M S L
T
0
T
1
M S L
↓ − − − − −
{x|y}
f : {0, 1, . . . , k − 1}
×n
→ {0, 1, . . . , k − 1} k
P
k
P
k

