Современные проблемы машиностроения
Подождите немного. Документ загружается.


V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
31
)(
)(
)cos(
0
2
urR
urc
(2)
и, ограничиваясь линейными членами ряда, получим
sin)(
cos
20
rR
uu
. (3)
Для нахождения угла относительного поворота обойм при приложении нагр узки
МСХ рассматривается как планетарный механизм [2, 3] и угол будет определяться при ве-
дущей звездочке
зв
и ведущей обойме
об
[2, 3]
зв
0
1
R
;
0
об
1
R
, (4)
где – радиус-вектор точки контакта ролика со звездочкой
0
= ( = 0).
Для оценки точности были проведены расчеты. При использовании выражения (3) по-
лучили расхождение в 1,33 % по сравнению с результатами на основе зависимости (2).
Таким образом, не обязательно производить интегрирование исходных уравнений для
получения зависимости для .
Известные зависимости [2, 3] для вычисления дают заниженные на 30 % и более ре-
зультаты по сравнению с экспериментальными. В известных [2, 3] моделях МСХ для нахож-
дения зависимости = (М) рассматривается совместное влияние деформаций и
1
и и
2
на
угол поворота центра ролика. Однако, сопоставление экспериментальных данных и резуль-
татов вычислений по зависимостям, полученным на основе этой модели МСХ, говорит о не-
корректности модели, на что указывает существенное расх ождение данных экспериментов и
расчетов.
Для определения угла изменим модель и построим еѐ, используя принцип суперп о-
зиции. Найдем вначале угол поворота
1
, возникающий от деформации и
1
, а затем определим
угол
2
, являющийся рез ультатом возн икновения деформации и
2
. Общий угол будет опре-
деляться как сумма
)()(
2211
uu
. (5)
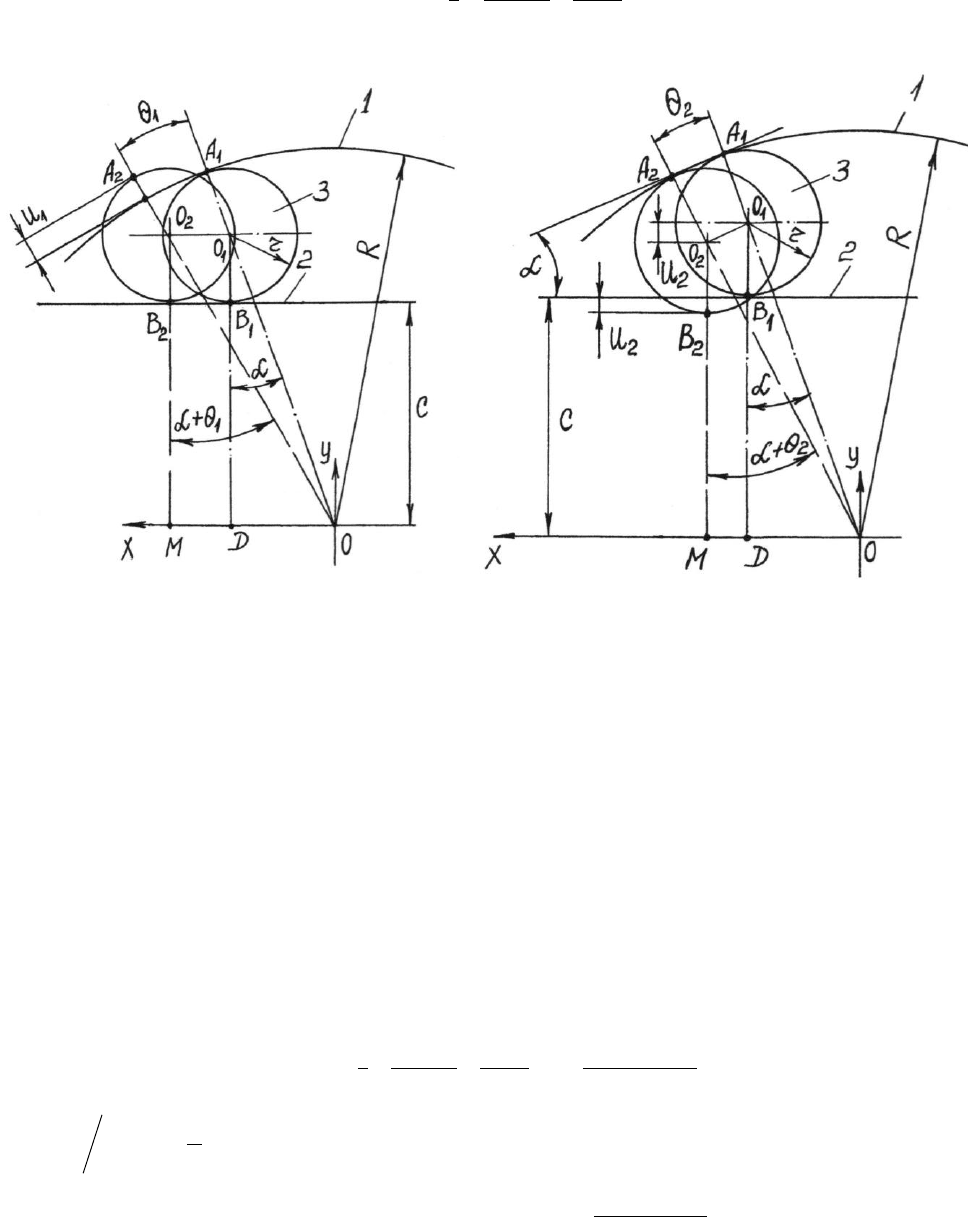
Рассмотрим МСХ с плоской рабочей поверхностью звездочки и определим угол
1
при условии, что он возникает за счет деформации и
1
(рис. 1), а ролик при этом перекатыва-
ется по плоской поверхности звездочки.
Из ОМО
2
(рис. 1) имеем
)(
)(sin
1
1
urR
OM
. (6)
Угол
1
на два порядка меньше угла . Поэтому sin ( +
1
) можн о разложить в ряд и
ограничиться линейными членами ряда. После преобразований на основе зависимости (6)
получаем
2/tg
1
1
l
u
, (7)
где l = R – r.
На основе рис. 2 имеем
rR
urc
2
2
)(cos
. (8)
Аналогичным образом на основе выражения (8) нетрудно получить
sin
2
2
l
u
(9)
и тогда общий угол
V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
32
sin2/tg
1
20
21
uu
l
, (10)
где u
0
= u
1
+ w.
Рис. 1
Рис. 2
Для проверки справедливости полученных решений были проведены вычисления для
роликового МСХ с плоской звездочкой и следующими параметрами: R = 70 мм; r = 7,5 мм;
l
р
= 25 мм; = 7;
0
= 55,063 мм; c = 54,534 мм.
Толщина обоймы S = 15 мм; число роликов z = 8; момент нагр узки M = 196 Нм.
В результате расчетов было получено
зв
= 0,0074036 рад.
Для данного МСХ экспериментальные данные дают
экс
зв
= 0,007947 рад, т. е. отклоне-
ние от экспериментов составляет 6,8 %.
При использовании известных зависимостей [3] будем иметь
изв
зв
= 0,0048175 рад и
отклонение от экспериментов составит 39 %.
Из приведенных рез ультатов видно, что полученные для решения позволяют иметь
достаточно близки е к экспериментам результаты и по точности значительно превосходят из-
вестные зависимости.
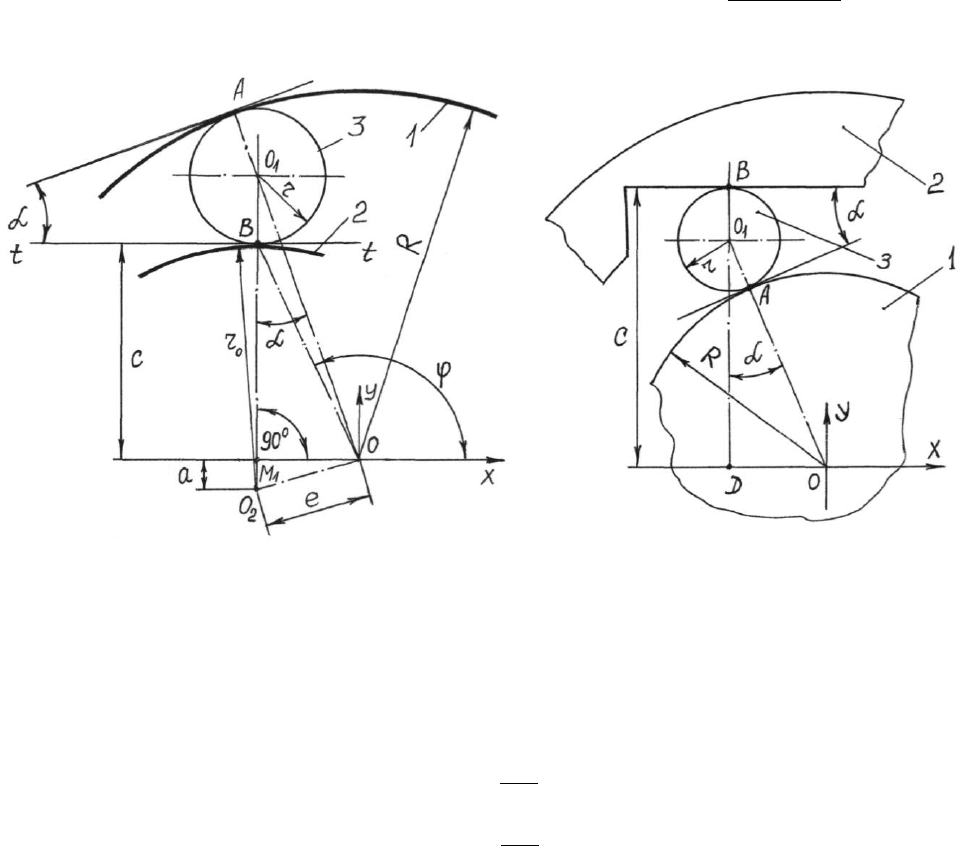
Аналогичным образом можно получить выражение для МСХ с криволинейной звез-
дочкой (рис. 3)
22
2
2
020
sin
5,0
1
sin2/tg
1
l
uruu
l
, (11)
где
l
a
cos1
.
Параметры а и r
0
обозначены на рис. 3. Член
1
sin
5,0
22
2
2
0
l
ur
и учитывает криво-
линейность звездочки. С точностью до величин порядка малости получаем выражение (10).
Проведенные вычисления п оказали отклонение от экспериментальных данных на 4,77 %.
V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
33
Если воспользоваться известными [3] зависимостями, т о отклонение от эксперимента будет
27,3 %.
Так при проведенных расчетах величина составляла = 0,003768.
Аналогичным образом можно получить выражение для МСХ с наружной звездоч-
кой (рис. 4). В случае плоской звездочки получаем выражение (10), где l = R + r. При криво-
линейной звездочке в выражении (11) l = R + r и перед членом
22
2
2
0
sin
5,0
l
ur
будет знак
минус.
Рис. 3
Рис. 4
Таким образом, с точностью для величин будем иметь общую зависимость (10).
Для динамических расчетов необходимо знать жесткость С
о
= dM/d МСХ. Имея
= (М) легко найти податливость е = d/dM, а затем определить жесткость С
о
= 1/е.
Обозначая в выражениях (4) U
зв
= (1 + R/
0
); U
об
= (1 +
0
/R) имеем
зв зв
θU
;
об об
θU
. (12)
Так как U
зв
и U
об
постоянны, то
зв
θ
e
d
U
dM
;
об
θ
e
d
U
dM
.
Учитывая, что угол = (u
1
; u
2
; w), то чтобы найти производную d/dM необходи мо
иметь выражения для u
1
; u
2
; w, которые определяются известными [4, 5] зависимостями.
Таким образом, полученные обобщенные зависимости позволяют подсчитать подат-
ливость МСХ, а вместе с этим и его жесткость.
Литература
1. Архангельский Г.В. Бесступенчатые импульсные передачи на баз е планетарных ме-
ханизмов. – Одесса: Друк, 2002. – 152 с.
2. Мальцев В.Ф. Роликовые механизмы сво бодного хода. – М.: Машиностроение,
1978. – 366 с.
3. Пилипенко М.П. Механизмы свободного хода. – М., Л.: Машиностроение, 1966. – 287 с.
4. Справочник машиностроения. Т.3. – М.: ГИТИМА, 1951. – 292 с.

V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
34
5. Биргер И.А., Шорр Б.Ф., Шнейдерович Р.М. Р асчѐт на прочность деталей машин. –
М.: Машиностроение, 1966. – 616 с.
ОБ ОСОБЕННОСТЯХ РАСЧЕТА ЦИЛИНДРИЧЕСКИХ
ПРЯМОЗУБЫХ ПЕРЕДАЧ НА КОНТАКТНУЮ ПРОЧНОСТЬ
Г.В. Архангельский, д.т.н., проф.
Одесская национальная академия пищевых технологий,
65039, Украина, г. Одесса, ул. Канатная, 112, тел. (0482)-47-52-15
E-mail: omnat@yandex.ru
А.И. Дубинец, д.т.н., проф.
Международный университет развития человека «Украина»,
04053, Украина, г. Киев, ул. Львовская, 23, тел. (044)-424-94-33
E-mail: office@vmurol.com.ua
Существующие методы расчѐта зубчатых передач на контактную прочность основаны
на рассмотрении условия прочности, когда точка зацеплен ия расположена в полюсе зацепле-
ния [1-6]. В зоне однопарного зацепления наибольшие контактные напряжения будут возни-
кать там, где приведенный радиус кривизны
п
будет принимать наименьшее значение.
В работе [7] показано, что наименьшее значение приведенный радиус кривизны при-
нимает в точке н (рис. 1), в которой происходит переход от двухпарного зацепления к одно-
парному и этот переход сопровождается скачкообразным приложением нагрузки.
Проведенные исследования [7] позволили получить формулы как для проверочного,
так и проектного расчѐта, рассматривая условие прочности в точке н. Однако, полученные в
работе [7] выражения не позволяют произвести сравнение с существ ующими зависимостями
и оценить величин у повышения напряжений в точке н по сравнению с напряжени ями в по-
люсе W зацепления (рис. 1). Поэтому п редставляется целесообразным произвести дальней-
шие исследования по изучению прочности зубчатых передач в окрестности перехода от
двухпарного зацепления к одн опарному.
Определим радиус кривизны
1н
профиля зуба шестерни в точке н, для которого мож-
но записать
bн
рвN
11
, (1)
где р
b
– шаг зубьев по основной окружности.
Отрезок N
1
в в линии зацепления представим так
a
a
d
вN
1
1
1
sin
2
, (2)
где d
la
– диаметр вершин зубьев шестерни, а угол
1a
обозначен на ри с. 1 и его можно опре-
делить из соотношения
1
1
1
1
2
1
cos
cos
z
d
d
w
a
b
a
, (3)
где d
1b
– диаметр основ ной окружности шестерни; z
1
– число зубьев шестерни;
w
– угол за-
цепления эвольвентных колѐс.
Имея cos
1a
нетрудно определить sin
1a
11
2
1
1
2
1
1
1
4
sin
2
1
1
cos1sin
zz
z
waa
. (4)

V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
35
В выражении (4) 1/z
1
<< 1 и поэт ому слагаемым 1/z
1
в выражении (4) как малой вели-
чиной можно для практических расчѐтов пренебречь и тогда выражение (4) примет вид
1
2
1
1
4
sin
2
1
1
sin
z
z
wa
. (5)
Рис. 1
Учитывая, что p
b
= p
w
cos
w
, p
w
= m, где m – модуль зацепления, и учитывая выра-
жения (2), (5) на основе соотношения (1) после преобразований получаем
w
w
wн
z
z
tg
2
sin
4
1
1
2
1
11
, (6)
где
1w
– радиус кривизны профиля зуба шестерни в полюсе w зацепления.
Приведѐнный радиус кривизны
nw
в полюсе зацепления представится известным вы-
ражением
wnw
u
u
1
1
, (7)
где u = z
1
/z
2
– передаточное отношение зубчатой передачи; z
2
– число зубьев колеса.

V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
36
Если обозначить:
2w
,
2н
– радиусы криви зны профиля зуба колеса в точках W и н, то
на основе рис. 1 можно записать
ннww 2121
. (8)
Из соотношения (8) имеется
нwwн 1122
. (9)
Так как
1w
>
1н
, то величина равная
нw 11
(10)
будет положительной.
Используя выражение (6) получаем
w
w
w
z
z
2
1
1
1
sin
4
1
tg
2
1
. (11)
Из выражения (9) следует
wн 22
. (12)
Используя соотношения (10) и (12) можно приведѐнный радиус кривизны
пн
в точке
н представить в виде
)1(1)1(
121
1
21
uu
u
u
w
www
w
нн
nн
. (13)
Так как > 0;
2w
–
1w
> 0, а
nw
w
u
u
1
1
, то из выражения (13) видно, что
пн
<
nw
.
Если обозначить в выражении (11)
w
w
z
z
x
2
1
1
sin
4
1
tg
2
1
, (14)
то
x
w
1
(15)
и тогда учитывая выражение (7) после преобразований получаем
u
xxu
wnwпн
1
)1(
2
1
. (16)
Обозначая
0
2
)1( zxux
выражение (16) приводится к виду
u
zu
wпн
1
0
1
. (17)
Так как
пн
<
nw
, то контактные напряжения на поверхности зубьев в точке н будут
больше, чем в полюсе W зацепления.
Используя выражение (17) для приведѐнного радиуса кривизны получим формулы,
позволяющие производить как проверочный, так и проектный расчѐт зубчатой прямозубой
передачи внешнего зацепления.
Если подставить в формулу Герца [8] значение приведѐнного радиуса к ривизны
пн
,
определяемого выражением (17), то после преобразований получим
012
1
zu
u
db
kF
zz
w
нt
нмн
, (18)
где F
t
– окружное усилие; k
н
– коэффициент расчѐтной нагрузки; b
2
– ширина колеса;
d
1w
– диаметр начальной окружности шестерни;
)1(
2
E
z
м
;
w
н
z
2sin
2
;
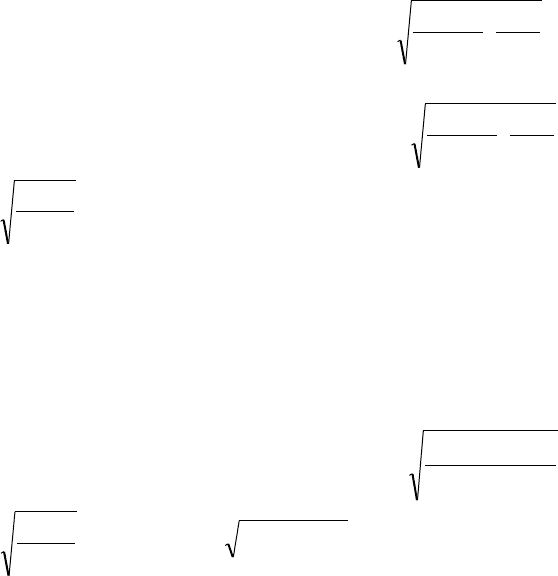
V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
37
Е – модуль нормальной упругости; – коэффициент Пуассона.
Здесь принято:
EEE
21
;
21
.
Полученное выражение (18) определяющее действительные контактные напряжения в
точке н, можно свести к известному выражению, определяющему контактные напряжения в
полюсе зацепления
u
u
db
kF
zz
w
нt
нмнw
1
12
. (19)
Если под корнем в выражении (18) умножить и разделить на u, то получим
u
u
db
kF
zzz
w
нt
nнмн
1
12
, (20)
где
0
zu
u
z
n
;
1
n
z
.
Назовѐм z
n
– коэффициентом числа зубьев шестерни, так как z
п
= z
п
(z
1
).
Из сравнения выражений (19) и (20) можно записать, что
nнwн
z
. (21)
Так как z
n
> 1, то
н
>
нw
.
Из выражения (20) после преобразований получаем формулу для проектного расчета,
определяющую межосевое расстояние a
w
передачи
2
2
2
][
)1(
нba
н
naw
u
kM
zuka
,
где
3
0
zu
u
z
n
;
1
a
z
;
3
22
5,0
нмa
Zzk
;
ba
– коэффициент ширины колеса относительно
межосевого расстояния; [
н
] – допускаемые контактные напряжения при расчѐте на уста-
лость.
При z
0
= 0 или z
п
= l получим известное выражение, определяющее a
w
в случае нахож-
дения зубьев в полюсе зацепления. В зоне однопарного зацепления коэффициент z
= l.
Как видно из выражения для z
п
величина этого коэффициента зависит от передаточно-
го отношения u. Проведенные расчѐты п оказали, что при u > 4, значения
н
превосходят
нw
на 10 % и более.
Литература
1. Добровольский В.А. Детали машин. гос. изд. техн. лит. УССР. – Киев, 1954. – 599 с.
2. Передачи зубчатые цилиндрические эвольвентные. Расчѐт на прочность. ГОСТ
21354 – 75. – М., 1976. – 61 с.
3. Детали машин / Л.А. Андриенк о, Б.А. Бойков, И.К. Ганулич и др. – М.: Изд-во
МГТУ им. Н.Э. Баумана, 2002. – 544 с.
4. Иванов М.Н. Детали машин. – М.: Высшая школа, 1976 – 399 с.
5. Решетов Д.А. Детали машин. – М.: Машиностроение, 1989. – 496 с.
6. Заблонский К.И. Детали машин. – К.: Вища школа, 1985. – 518 с.
7. Фарков Г.С., Скрачковский Г.Г. Расчѐт з убьев передач на контактную прочность //
Вестник машиностроения. – №12. – 2003. – С. 19-21.
8. Тимошенко С.П., Гудьер Дж. Теория упругости. – М.: Наука, 1979. – 560 с.
V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
38
ИССЛЕДОВАНИЕ ДИНАМИКИ ПОВОРОТНОГО МЕХАНИЗМА
МНОГОПОЗИЦИОННОГО СТОЛА АГРЕГАТНЫХ СТАНКОВ
И.К. Битуев, к.т.н., доц., A.А. Афанасьева, к.т.н., доц.
Восточно-Сибирский государственный технологический университет,
670013, Бурятия, г. Улан-Удэ, ул. Ключевская 40В, тел.(3012)41-05-35
E-mail: bitueva_elv@mail.ru
В производственной практике эксплуатации агрегатных станков имеют место сл учаи,
когда при повороте позиционного стола без видимых причин возникают большие динамиче-
ские нагрузки. Эти нагрузки приводят к быстрому из носу отдельных деталей, потере задан-
ной точности и нарушения цикла работы станка [1-4]. В связи с этим возникла задача изуче-
ния процесса поворота позици онного стола с учетом влияния факторов, определяющих ре-
альные условия его работы
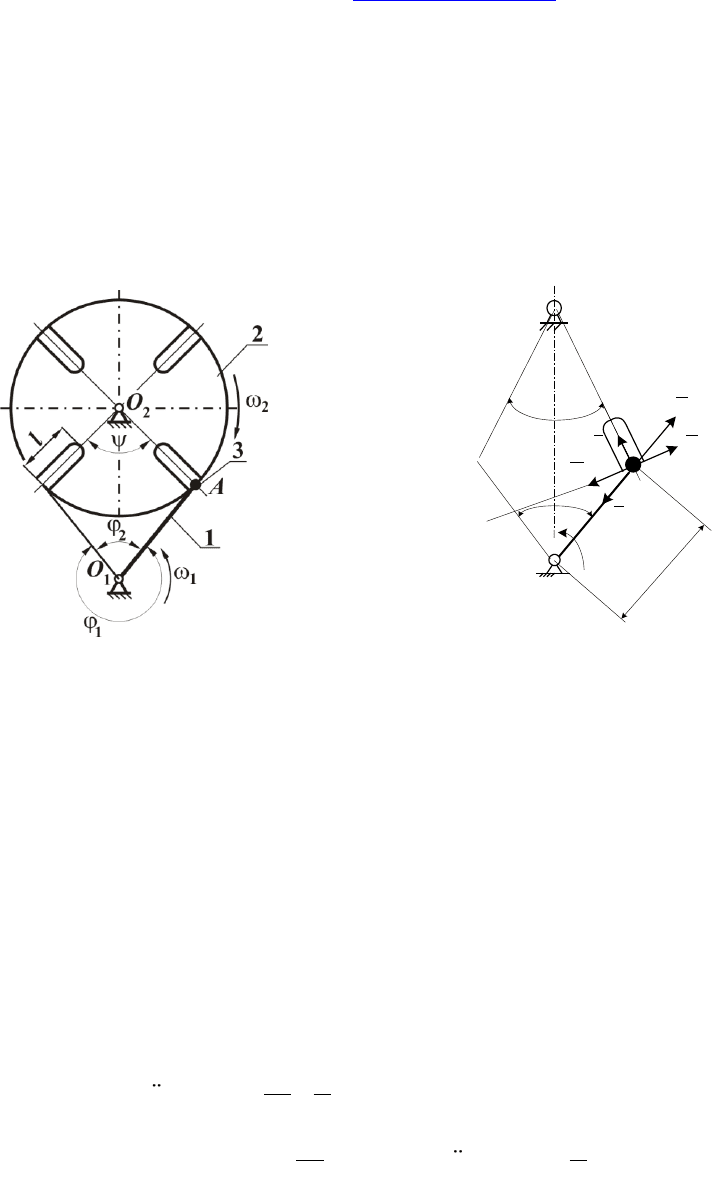
В качестве поворотного механизма для периодического вращения многопозиционного
стола применяется мальтийский механизм с внутренним или внешним зацеплением и ради-
альным расположением пазов.
Рис. 1.
1 – кривошип; 2 – кулачок; 3 – палец
Рис. 2.
Расчетная схема
В таки х механизмах, где имеются п оворотные столы с мальтийскими механизмами,
возникает проблема износа поверхностей пазов в этих механизмах. По сути, палец кривоши-
па, который находится в пазу, имеет сложное движение. Расстояние пальца с точечной мас-
сой m на свободном конце кривошипа является переменной до неподвижной оси кулачка,
которая перпендикулярна к этой плоскости. Отсюда можно сделать вывод, что момент инер-
ции пальца относительно этой оси переменная величина:
2
2 2 2
,
Z
I I mh H a h R
,
где
12
H OO
.
Следовательно, т ребуется рассмотреть относительное движение пальца – движение
его по пазу кулачка при равномерном дви жении кривошипа в одн у сторону. Р ас смотрим рис.
1, в котором показан механизм поворота в горизонтальной плоскости. Составим дифферен-
циальные уравнения при относительном движении пальца (1):
ии
2
е 1 кор 2
υ
ψ
cos , 0 , 0
22
mx F N F G N
, (1)
2
2π
υ π ψ, ψ , 4z
z
, то
22
1
ψ
ω cos 0
2
xa
.
2
1
2
O
1
O
A
a
en
a
и
е
F
и
кор
F
1
N
r
v
x
y
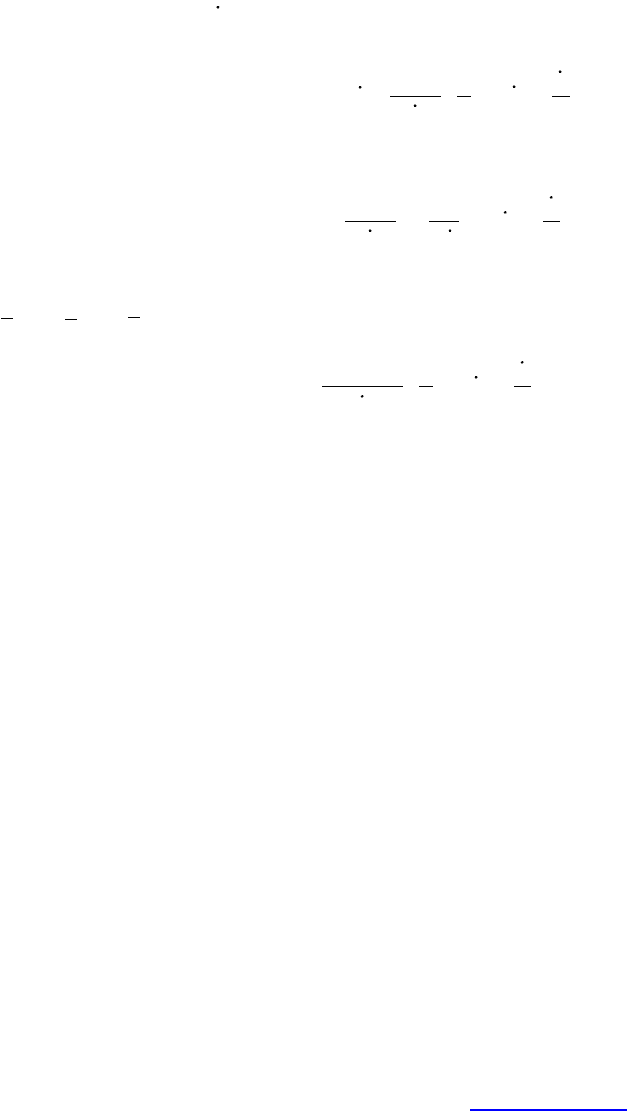
V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
39
Ускорение пальца зависит от закона изменения угла поворота кулачка.
Пусть
ψ ( )ft
носит переменный характер, в т.ч. кратковременное движение с по-
стоянной скоростью
ψ
. Тогда получим закон изменения относительной скорости при движе-
ния пальца:
2
1
ω2
1 ψ
sinψ
ψ 4 2
a
x t t
при движения пальца с относительного покоя и закон относительного дви жения пальца как
точки:
2
2
1
ω2
1 ψ
cosψ
ψ 4ψ 4
a
x t t C
.
Проверить правильность закона относительного движения можно датчиками при экс-
перименте. Также найдено выражение при давлении точки (пальца) на стенки паза
12
N N j N k
, где
3
1
12
4ω2
1 ψ
sinψ,
ψ 4 2
ma
N t t N mg
.
Время движения точки внутри паза в одну и обратную стороны кратковременны, по-
этому резко меняется характер движения и усилия на стенки паза, что видно и з найденных
выражений, как следствие, приводящее к интенсивном у износу пазов мальтийского меха-
низма и увеличению динамических нагрузок.
Литература
1. И.И. Вульфсон. Колебания в машинах. Издание третье, дополненное и исправлен-
ное. Санкт - Петербург, 2008.
2. М.С. Комаров. Динамика механизмов и машин. – М.: Машиностроение. – 1969 г.
3. Б.И. Павлов, В.Д. Очиров. Вычислительный эксперимент в динамике машин и ме-
ханизмов. – М.: «Наука». – 1981 г.
4. Е.Г. Нахапетян. Контроль и ди агностирование автоматического оборудования. – М.:
«Наука» – 1990 г.
5. Ф.К. Королев, И.Л. Цымбал. Динамический расчет поворотного механизма позици-
онного стола агрегатных станков. – Вестник Харьковского политехнического института, №1 –
(49). – выпуск 1. – 1974 г.
РАСЧЁТ НАПРЯЖЁННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ В ДЕТАЛЯХ
ИЗ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ С ПРИМЕНЕНИЕМ
ФУНКЦИИ НАПРЯЖЕНИЙ
П.В. Бреховских
Казанский государственный технический университет имени А. Н.Туполева.
420111, Казань, ул. К.Маркса,10, тел.: (843) 231-03-25
E-mail: pav-89@mail.ru
Применение композитных материалов (КМ) в различных отраслях техники непрерыв-
но расширяется. Такие свойства, как высокая удельная прочность, износостойкость, хорошее
сопротивление к воздействию агрессивных сред, наконец, высокая технологичность, делают
композиты незаменимыми для использования в разнообразных конструкциях машинострое-
ния и особенно в авиакосмической технике, где изделия работают в экстремальных условиях,
с жесткими весовыми ограничениями и повышенными требованиями к надежности.
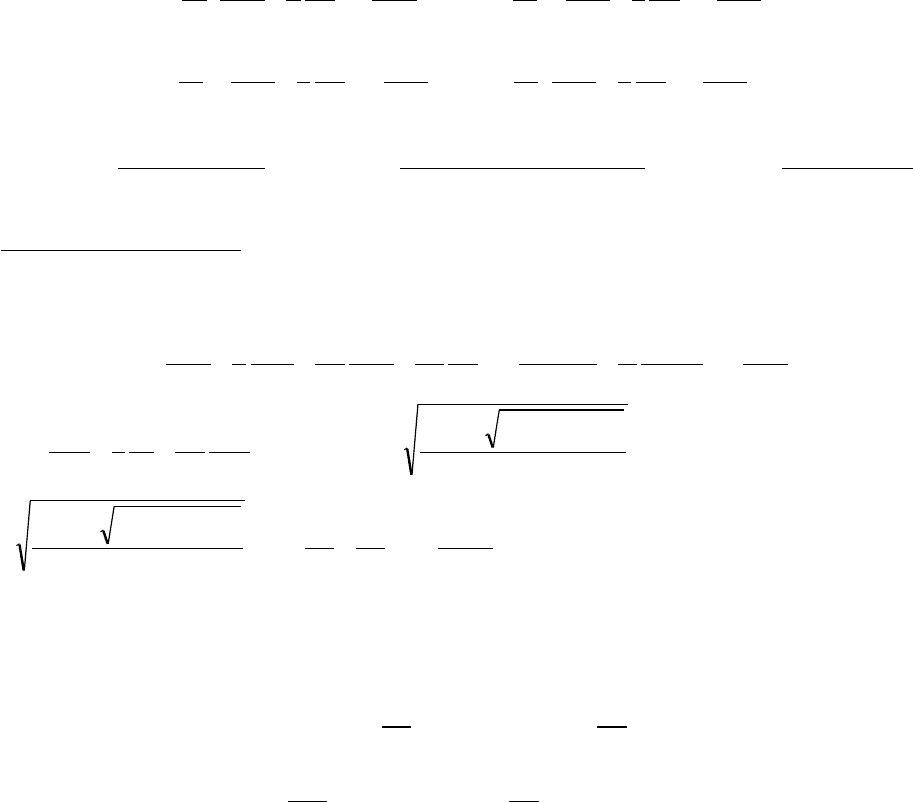
V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
40
Однонаправленные композиционные детали (трубы, стержни, профили, оболочки и
др.), в том числе тела вращения, составляют значительную часть в конструкциях современ-
ных ЛА. Рассматриваются некоторые решения задачи деформирования авиационных конст-
рукций из трансверсально-изотропного материала, использующие полиномиальные решения
системы уравнений линейной теории упругости для анизотропной среды в случае осесим-
метричной деформации.
При осесимметричной деформации трансверсально-изотропного тела все напряжения
могут быть выражены через одну фун кцию напряжений:
;
2
2
2
2
z
a
rr
b
r
z
r
;
2
2
1
2
2
z
a
rr
r
b
z
;
2
2
2
2
z
d
rr
c
r
c
z
z
2
2
2
2
z
a
rr
c
r
z
rz
, (1)
где
;
2
133311
)
1211
(
13
aaa
aaa
a
;
2
133311
3312
)
4413
(
13
aaa
aaaaa
b
;
2
133311
2
12
2
11
aaa
aa
d
;
2
133311
4411
)
1211
(
13
aaa
aaaaa
c
ij
a
упругие постоянные материала.
При этом функция должна удовлетворять следующему уравнению:
,0
4
4
2
3
22
4
3
1
2
2
2
1
3
3
2
4
4
z
B
zr
r
A
zr
A
r
rrrr
r
r
(2)
где
);2,1(
2
2
2
11
2
2
i
z
i
s
rr
r
i
;
2
4
2
)(
1
d
dcaca
s
d
dcaca
s
2
4
2
)(
2
;
2
2
2
1
1
;
2
2
1
2
1
1
ss
B
ss
A
.
В работе найдено полиномиальное решение уравнен ия (2) в виде
2 2 2 3
( , ) ( , )
1 2 02 22 3 13 33
1
8
4 4 2 2 4
4 04 24
33
8
4 5 2 3 5
...... ( , ).
5
15 35
15 5
N
r z A U r z A A c r c z A c r z c z
A
A c r z c r z z
BB
A
A c r z z c r z z A U r z
NN
BB
(3)
Граничные условия в случае заданных н а боковой поверхности усилий
n
R
и
n
Z
сво-
дятся к условиям на меридиане поверхности вращения и имеют следующий вид:
.),cos(),cos(,),cos(),cos(
n
Zzn
z
rn
rzn
Rzn
rz
rn
r
(4)
Произвольные коэффициенты
A
, входящие в решение (3) подлежат определению.
Их количество зависит от выбора метода решения граничной задачи. Коэффициенты разло-
жения
A
, обеспечивающие наил учшую аппроксимацию граничн ых условий (4) найдем с
помощью метода взвешенных невязок или метода коллокаций.
Процедура, описанная в работе по нахождению полиномиальных решений по рекур-
рентной формуле, дает достаточно простой алгоритм для последовательного построения по-
