Современные проблемы машиностроения
Подождите немного. Документ загружается.


V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
21
где
00
0,5M P D
– величина момента предварительного поджатия.
Рассмотрим дифференциальное уравнение прогибов v
(z) ЭС в статике, на которые за-
меняется ПМВД [4]:
21
( ) ( )
( ) 1 ''( ) 0,
IV
N z N z
v z v z
AA
(4)
с характерными зависимостями для балки Тимошенко
1
2
1
( ) ( ) / (1 ( )/ );
( ) ( );
( ) ( ( ) ( )).
z v z N z A
M z A z
Q z A v z z
(5)
Дифференциальное уравнение (4) является нелинейным, вследствие переменной по
длине ЭС продольной силы N(z) = var:
2
3
0
0
0
( ) ( ( )) , витки ПМВД-разомкнуты
2
()
1/
()
( ) , витки ПВМВД-сомкнуты
0,5 3 /
l
n
n
A
P P v z dz
l
Nz
BB
Mz
PP
D B B
(6)
и следующих краевых условий закрепления шатуна:
(0) 0;
( ) ( ) (1 cos ( ));
(0) 0;
( ) ( ) ( ) 0.
v
v l l f r l
M l Q l f N l R
; (7)
Нелинейное дифференциальное уравнение (4) с краевыми условиями (7) можно све-
сти к рению задачи Коши:
; ; ; ,
dv d dM dQ
MQ
dz dz dz dz
(8)
с начальными условиями
(0) 0; (0) 0; (0) ; (0) ,v M m Q q
(9)
где
* * * 2 * 3
11
2 2 1 2
()
(1 ) (1 2 ) ( ) ( ) ;
o
RR
PP
AA
k M k M M
A A A A
12
(0) (1 )/ ;m M k A
2
12
(0) (1 ) / ;q Q k A
2
1
1/
1
;
3 / 1
n
R
n
BB
A
A
R B B k
1 0 1
( ( ) )/k P P A
.
Поиск начальных условий (9) осуществлялся по схеме последовательных приближе-
ний метода Ньютона [6]:
11
(2) (1)
1
(2) (1)
2 2 2
,
mm
mq
qq
mq
V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
22
где
1
,
2
– функции, зависящие от неизвестных начальных условий m и q и условий за-
крепления шатуна:
*
1
( , ) ( , , ) ( , , ) * ;m q v l m q l m q f
* * *
2
( , ) ( , , ) ( , , ) ;
R
m q M l v q Q l m q f M
*
1
/(1 );f f k
0
1
2
()
(1 )
R
PP
M k R
A
.
В качестве первого приближения, рассматривалась линейная постановка с допущени-
ем о постоянстве по длине ЭС продольной силы – N(z) = P(∆)= const, что позволило свести
уравнение (4) к линейному вида
2
( ) ''( ) 0,
IV
v z k v z
(10)
где
2
21
( ) ( )
(1 ).
PP
k
AA
Решение уравнения (10) может быть предоставлено с помощью нормальной системы
фундаментальных функций
( )( 1,4)
i
V z i
в следующем виде [7]:
1 1 2 2 3 3 3 3
( ) ( ) ( ) ( ) ( ),v z C V z C V z C V z C V z
где постоянные интегрирования
( 1,4)
i
Ci
получены из условия закрепления шатуна (7).
Отметим, что в математическую модель расчета шатуна можно также включить до-
полнительную распределенную поперечную нагрузку
0
()qz
, в которой, с одной стороны,
можно учесть массу витков ПМВД, с другой стороны, учитывать силы их инерции при вра-
щении обоймы шатуна (принимая их как статическую нагрузку). Кроме того, дополнитель-
ные силы инерции от вращения обоймы шатуна могут быть учтены в краевых условиях (7)
при определении угла поворота
()l
шатуна в сечении z = l.
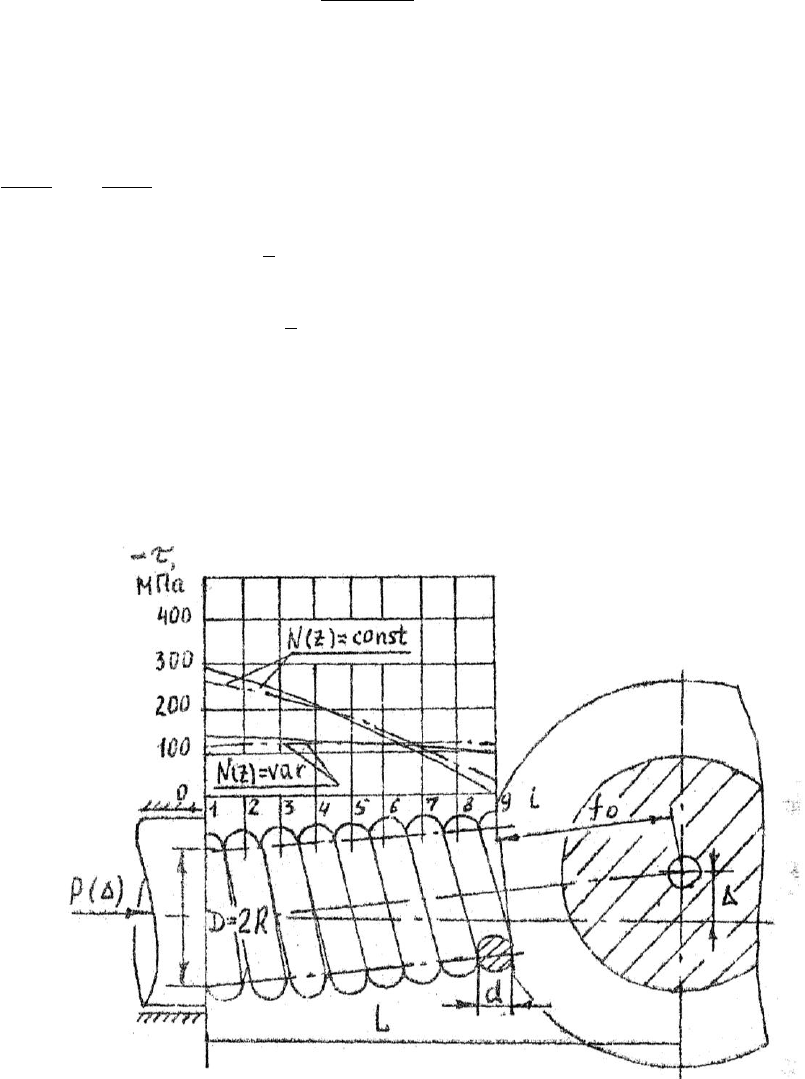
Рис. 2. Результаты расчета касательных напряжений τ в витках ПМВД,
используемой в качестве шатуна поршневой машины

V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
23
На рис.2 представлены результаты расч етов касательных напряжений:
/k M W
(
k
– коэффицие нт, учитывающи й кривизну витков ПМВД;
W
– пол ярный момент сопро-
тивления сечения витка ПМВД) по ли нейной (N
(z) = const) и нелинейной (N
(z) = var) мо-
делями по виткам ПМВД с шагом ∆z = d (d – диаметр витка ПМВД) для малогабаритной
поршневой машины: Р(∆) = 14, 7Н; ∆ = 1·10
-3
м; d = 1·10
-3
м; D = 5·10
-3
м; i
p
= 8; l = 7·10
-3
м;
f
0
= 15·10
-3
м; L = 23·10
-3
м). В расчетах также учте ны дополнит ельные дина мические на-
пряже ния, в озникающие вследствие вращения обоймы шатуна малогабаритной поршневой
машины.
Полученные рез ультаты хорошо согласуются с комплексом ресурсных испытаний шату-
нов, выполненных в виде ПМВД, работающих в составе малогабаритных поршневых машин [8].
Литература
1. Грезин А.К. Микрокриогенная техника / А.К. Грезин, В.С. Зиновьев. – М.: Маши-
ностроение, 1977. – 232 с.
2. А. с. 1101632 СССР, МКИ
4
. Газовая криогенная машин а / А.В. Бородин и др.
(СССР) // Открытия. Изобретения, 1984. – № 25.
3. А. с. 1101632 СССР, МКИ
4
. Газовая криогенная машин а / А.В. Бородин и др.
(СССР) // Открытия. Изобретения, 1989. – № 34.
4. Хвингия М.В. Вибрации пружин / М.В. Хвингия. – М.: Машиностроение, 1969. –
288 с.
5. Губанова И.И. Устойчивость пружин с сопр икасающим ися витками при сжатии /
И.И. Губанова. // Вопросы динамики и прочно сти. – Рига: АН Латв. ССР, 1962. – Вы п. 8.
– С. 52-64.
6. На Ц. Вычислительные методы решения прикладных граничных задач /Ц. На. – М.:
Мир, 1984. – 296 с.
7. Вибрации в технике: Справочник. В 6-ти т. / Ред. совет: В.Н. Челомей (пред.). – М.:
Машиностроение, 1978. – Т.1. Колебания линейных систем / Под ред. В.В. Болотина. – 1978.
– 352 с.
8. Бородин А.В. Применение пружин растяжения в приводе вытеснителя криогенного ох-
ладителя / А.В. Бородин и др. // Химическое и нефтяное машиностроение. – 1989. – № 5. – С. 17.
ОПИСАНИЕ ЭВОЛЬВЕНТНЫХ ПОВЕРХНОСТЕЙ ЗУБЬЕВ
ЦИЛИНДРИЧЕСКИХ КОСОЗУБЫХ КОЛЕС ВЕКТОРНЫМИ ФУНКЦИЯМИ
С.П. Андросов, к.т.н., доц., И.Г Браилов
*
, д.т.н., проф.
Омский государственный технический университет,
644050, г. Омск, пр. Мира, 11 тел. (3812) – 652-026,
E-mail: asp57@list.ru
*
Сибирская государственная автомобильно-дорожная академия,
644080, г. Омск, пр. Мира, 5 тел. (3812) – 651-176
Вопросы моделирования формообразования зубьев косозубых колес при зубообра-
ботке в п ространственном отображении т ребуют рассмотрения н е только профиля зуба в
торцевом сечении, но и всей боковой поверхности зуба.
Настоящая работа посвящена описанию боковых винтовых эвольвентных поверхно-
стей зубьев цилиндрических косозубых колес параметрическими векторными функциями.
Зубья зубчатых колес, применяемых в машиностроении, представляют собой тела,
образуемые двумя симметричными эвольвентными поверхностями, называемые теоретиче-
скими. У реального зуба не вся боковая поверхность совпадает с теоретической [1]. В осно-
V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
24
вании зубьев в большинстве случаев между теоретической и поверхностью впадин имеется
переходная поверхность. В данн ой статье рассматривается винтовая эвольвентная теоретиче-
ская поверхность.
В работе [2] определена зависимость, описывающая эвольвентный профиль в торце-
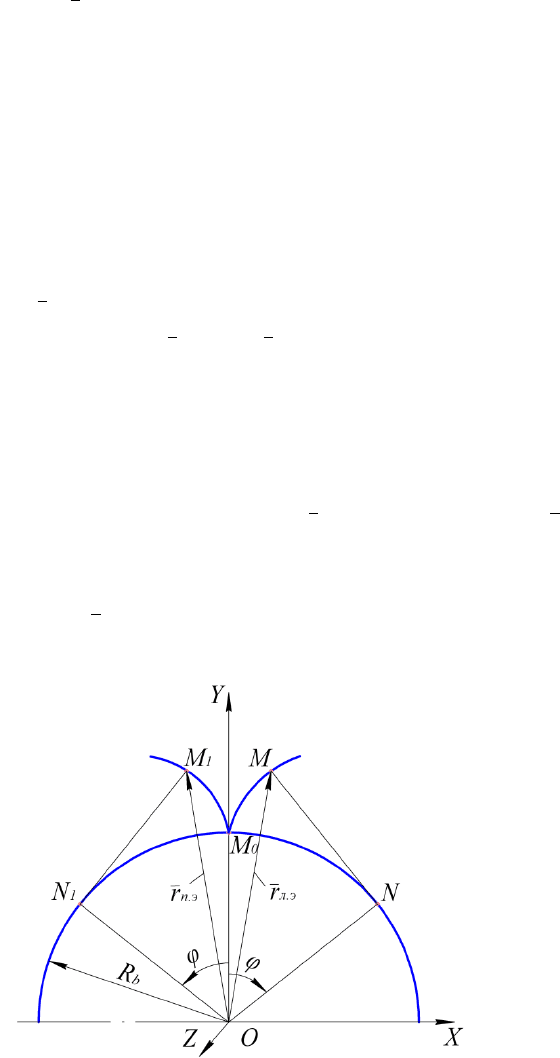
вом сечении виде векторной ф ункции
0
)sin(cos
)cos(sin
.
b
b
эп
R
R
r
, (1)
где R
b
– радиус основной окружности (рис. 1); φ – угол развернутости эвольвенты.
Формула (1) описывает правую, относит ельно оси OY, эвольвентную кривую М
0
М
(рис. 1), соответств ующ ую профилю зуба только с одной стороны. При этом, отмети м, что
эвольвентная кривая рассматривались в координации, когда ось ОУ проходит через началь-
ную точку эвольвенты М
0
, расположенную на основной окружности радиуса R
b
.
Второй эвольвентный п рофиль М
0
М
1
образ уется таким же образом, как и профиль
М
0
М, только в этом случае образ ующая прямая
11
MN
перекатывается по основной окр ужно-
сти в другую сторону.
Векторная функция
эл
r
.
левой эвольвентной кривой М
0
М
1
определяется выражением
эпэл
rMr
..
,
где [M] – матрица поворота вокруг оси OY на 180 градусов:
100
010
001
M
.
После перемножения матрицы [M] и функции
эп
r
.
векторная функция
эл
r
.
принимает
вид:
0
)sin(cos
)cos(sin
.
b
b
эл
R
R
r
.
Рис.1. Образование эвольвенты
Рассматривая эвольвентные поверхности (рис. 2), отметим, что зубья косозубого ко-
леса в торцевом сечении имеют эвольвентный профиль. При этом на любом фиксированном
радиусе колеса совокупность точек, принадлежащих боковой поверхности зуба, в направле-
нии его оси образует винтовую линию.

V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
25
Рис. 2. Эвольвентные поверхности
Положение п роизвольной точки М правой винтовой эвольвентной пов ерхности
М
0
АА'М
0
' косого зуба определяется векторной функцией
1
11
11
..
sincos
cossin
a
R
R
r
b
b
пэп
,
где υ
1
– угол поворота проекции вектора
пэп
r
..
на плоскость XOY;
a
– параметр, ха-
рактеризующий движение по винтовой линии вдоль оси колеса OZ [3].
Текущий параметрический угол φ
1
изменяется в пределах от своего нулевого зн аче-
ния, до значения φ
1max
, которое он принимает на тыльном торцевом сечении зубчатого коле-
са. Величина φ
1max
определяется по формуле
b
b
tg
R
b
max1
,
где β
b
– угол наклона линии зуба на основном цилиндре; b – ши рина зубчатого венца.
Соответственно положение произвольной точки М' левой винтовой эвольвентной по-
верхности М
0
ВВ'М
0
' (рис. 2) описывается векторной функцией
1
11
11
..
sincos
cossin
a
R
R
r
b
b
пэл
.
Для образования формы зуба з убчатого к олеса необходимо эвольвентные поверхно-
сти расположить так, чтобы он и охватывали его тело. При этом векторы, определяющие
эвольвентные поверхности, требуется повернуть на угол ψ. Правую эвольвентную поверх-
ность следует поворачивать против часовой стрелки, а левую – по часовой стрелке. Опреде-
ление угла поворота ψ показано на рис. 3, на котором представлено фронтальное торцевое
сечение зубчатого колеса.
V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
26
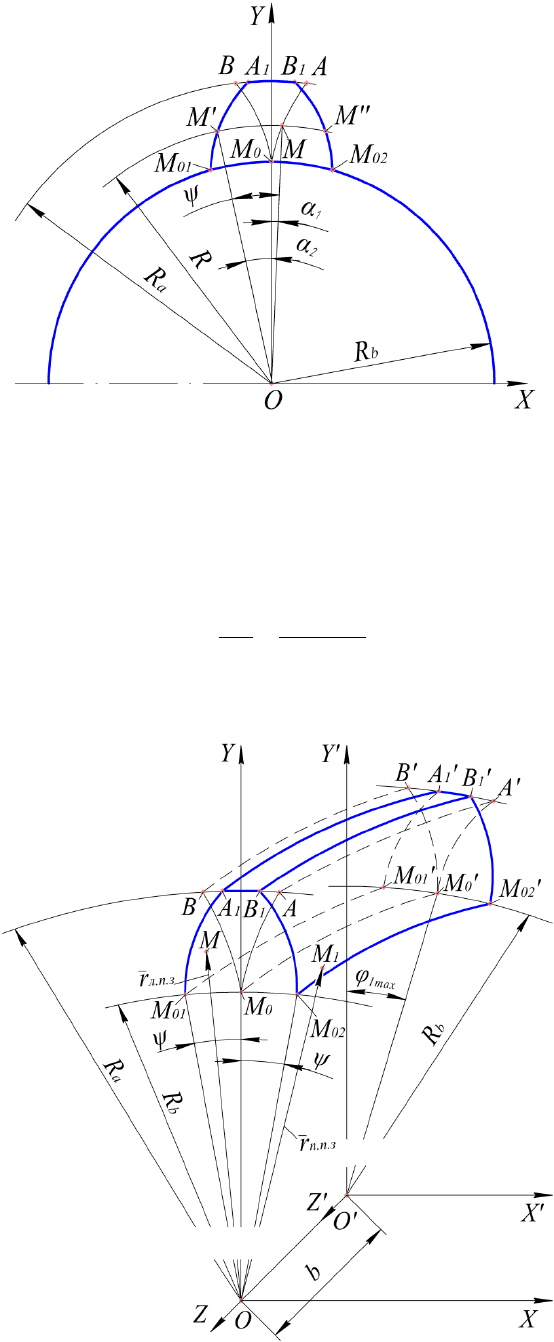
Рис. 3. Фронтальное торцевое сечение зубчатого колеса
При нахождении угла ψ учитывается, что толщина зуба
MMS
t
по делительной
окружности радиуса R имеет заданное значение. Угол поворота ψ равняется сумме углов
21
. (2)
В формуле (2) угол α
1
является эвольвентным углом в точке М, а угол α
2
определяется
зависимостью
cos44
2
R
m
R
P
nt
,
где
t
P
− окружной шаг зубьев;
n
m
− нормальный модуль зубьев; β − угол наклона зубьев по
делительному цилиндру.
Рис. 4. Боковые эвольвентные поверхности зуба

V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
27
Векторная функция левой боковой винтовой эвольвентной поверхности зуба М
01
А
1
А
1
'М
01
'
(рис. 4) косозубого колеса запишется:
пэпрзпл
rMr
..1..
,
где [M
1
] − матрица поворота на угол ψ против часовой стрелки:
100
0cossin
0sincos
1
M
.
После преобразований векторная функция
зпл
r
..
принимает вид:
1
11
11
..
sincos
cossin
a
R
R
r
b
b
зпл
, (3)
Соответственно векторная функция правой боковой винтовой эвольвентной поверх-
ности зуба М
0 2
В
1
В
1
'М
02
' косозубого колеса запишется:
пэлзпп
rMr
..2..
,
где [M
2
] − матрица поворота на угол ψ по часовой стрелке:
100
0cossin
0sincos
2
М
.
После преобразований векторная функция
зпп
r
..
принимает вид:
1
11
11
..
sincos
cossin
a
R
R
r
b
b
зпп
. (4)
Формулы (3) и (4) описывают боковые винтовые эвольвентные поверхности первого
зуба зубчатого колеса (рис. 5). Второй и последующие зубья колеса описываются векторны-
ми функциями, получаемых путем умножения функций (3) и (4) на матрицу
100
0cossin
0sincos
3 ii
ii
М
, (5)
где
z
i
i
21
.
Рис. 5. Зубчатое колесо
В формуле (5) номер зуба i изменяется от 1 до числа зубьев z.

V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
28
В результате, определены зависимости для описания боковых винтовых эвольвентных
поверхностей всех зубьев цилиндрического косозубого зубчатого колеса, выраженные пар а-
метрическими векторными функциями, необходимых при моделировании формообразования
в процессе зубообработки.
Литература
1. Болотовский И.А., Гурьев Б.И., Смирнов В.Э., Шендерей Б.И. Цилиндрические
эвольвентные зубчатые передачи внешнего зацепления. – М.:Машиностроение, 1974. – 160 с.
2. Браилов И.Г., Андросов С.П. Описание эвольвенты векторной функцией, выражен-
ной в параметрах станочных систем // Проблемы механики современных машин: материалы
четвертой Международной научно – практической конференции в 3 т. – Улан-Удэ: ВСГТУ,
2009. – Т. 2. – С. 11-14.
3. Браилов И.Г., Андросов С.П., Адмаев С.С. Боковая поверхность зуба цилиндрических
зубчатых колес. Известия Самарского научного центра РАН, Т. 12, 1(2), 2010. – С. 310-312.
К ОПРЕДЕЛЕНИЮ СИЛ, ДЕЙСТВУЮЩИХ НА ЗВЕНЬЯ ВОЛНОВЫХ ПЕРЕДАЧ
С ПРОМЕЖУТОЧНЫМИ ТЕЛАМИ КАЧЕНИЯ
Ан И-Кан, д.т.н., проф., Д.В.Беляев, асс.
НИ Томский политехнический университет,
634050, г.Томск, пр.Ленина,30, тел.(3822)-563-496
E-mail: dvb@tpu.ru
В последнее время активно исследуются и внедряются в машиностроении волновые
передачи с промежуточными телами качения. Один из примеров таких п ередач представлен
на рис. 1. Данная передача содержит: центральное колесо 1, промежуточные тела 2, сепара-
тор 3 и кулачок 4. В указанных передачах в зацеплении одновременно может находиться по-
ловина всех промежуточных тел. Благодаря указанному факту создается многопарность за-
цепления, которое благоприятствует созданию механизмов с улучшенными свойствами.
Рис. 1. Пример волновой передачи с роликовыми промежуточными телами
V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
29
Однако малая изученность и некоторые просчеты в исследовании такого рода передач
создают препятствия к их более широкому применению. Среди некоторых «белых пятен » в
расчетах является раскрытие статической неопределимости при определении усилий между
промежуточными телами качения и сопрягаемыми деталями. Восполн яя этот пробел, пред-
лагается одна из методик по аналогии с предложенной проф. В.Н.Кудрявцевым в [1].
Суть нашей методики заключается в следующем. Мысленно зафиксируем подвижный в
данной передаче сепаратор 3, а к кулачку 4 приложим крутящий момент, от которого он по-
вернется на какой-то угол в результате деформации всех контактируемых элементов передачи.
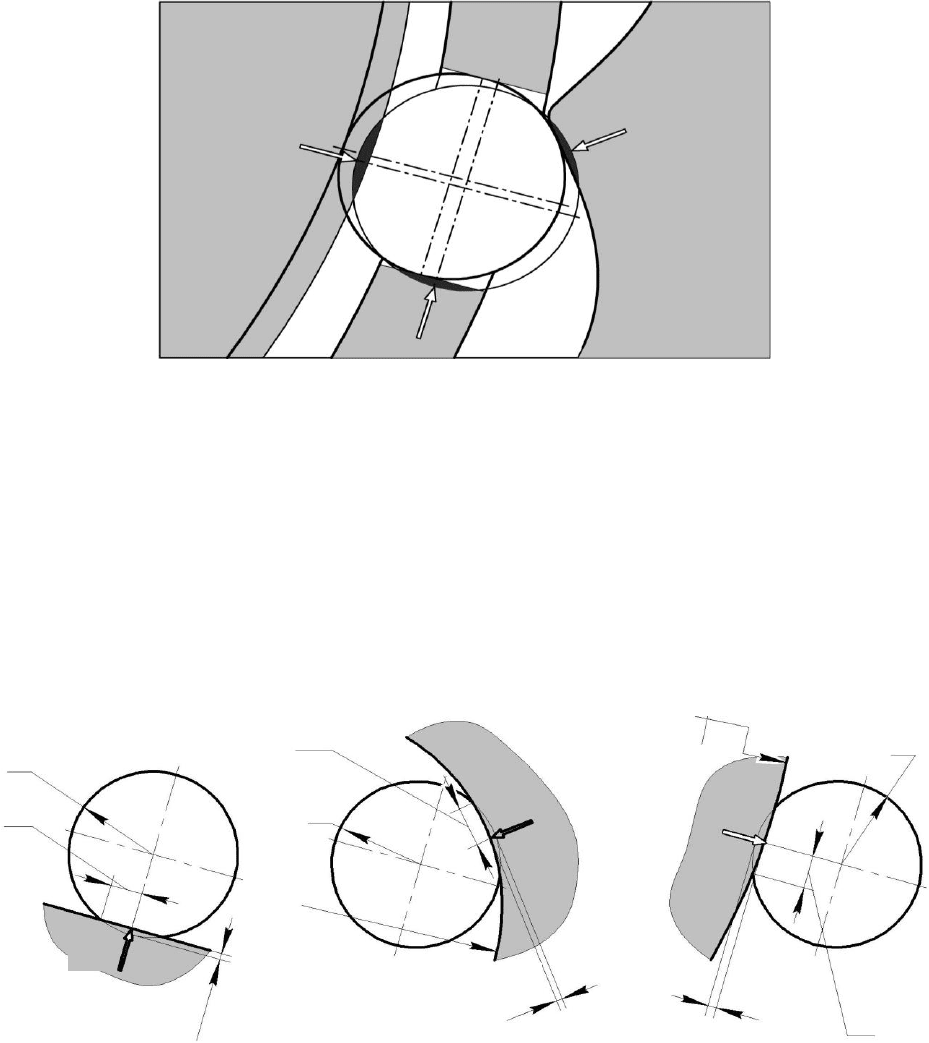
Рис. 2. Выносной элемент Б (увеличено)
Рассмотрим отдельно взятый узел, представленный на рис. 2 в качестве выносного
элемента Б из рис. 1. На промежуточное тело 2 со стороны деталей действует сразу три силы
F, Q и P, представляющие собой систему сходящихся сил в геометрическом центре промежу-
точного тела. Таким образом, имеется три схемы касания промежуточного тела окружающи-
ми его деталями рис. 3. Найти деформацию, а также остальные параметры в каждой схеме
возможно по зависимостям, представленным в [2].
Задавшись силой в узле, например, действующей со стороны кулачка 4 на промеж у-
точное тело 2, найдем величину деформации деталей в рассматриваемом узле. Посколь ку все
процессы связаны между собой, то по известной деформации в одном узле, найдем ее и в
других работающих узлах передачи. Решая обратную задачу - нахождения сил по величине
деформаций, определим искомые усилия, действующие во всех узлах.
Литература
1. Планетарные передачи / В.Н.Кудрявцев. – 2-е изд., перераб. и доп . – М.-Л.: Маши-
ностроение, 1966. – 307 с.
P
F
N
R
b
b
b
r
r
r
Δ
Δ
Δ
N
P
F
R

V Международная научно-техническая конференция
«Современные проблемы машиностроения»
______________________________________________________________
30
2. Справочник по сопротивлению материалов / Г.С.Писаренко, А.П.Яковлев,
В.В.Матвеев. – Киев: Наукова думка, 1975. – 704 с.
ОПРЕДЕЛЕНИЕ УПРУГИХ СВОЙСТВ РОЛИКОВЫХ МЕХАНИЗМОВ
СВОБОДНОГО ХОДА
Г.В. Архангельский, д.т.н., проф.
Одесская национальная академия пищевых технологий,
65039, Украина, г. Одесса, ул. Канатная, 112,
тел. (0482)-47-52-15
E-mail: omnat@yandex.ru
Роликовые механизмы свободного х ода (МСХ) широко используются в системе при-
вода самых различных машин и приборов, применяемых в различных отраслях промышлен-
ности [1-3]. МСХ применяются в управляемых импульсных вариаторах, импульсных редук-
торах, автоматических инерционных передачах, гидротрансформаторах, многодвигательных
приводах, металлорежущих станках, трубопрокатных станках, главных приводах вертолетов
и специальных приводах самолетов, приводах резервных генераторов, стартерах автомоби-
лей, в системе привода рабочих органов сельскохозяйственных машин и т.д.
МСХ в системе агрегата в большинстве случаев являются наиболее слабыми звенья-
ми, ограничивающие надежность и долговечность агрегата.
Заклинивание или включение МСХ сопровождается возникновением колебательного
процесса, в результате чего МСХ нагружается динамическим моментом. Для исследования
динамики агрегатов с МСХ необх одимо знать жесткость МСХ, для определения которой в
настоящее время строят упругую характеристик у, т.е. з ависимость угла относительного по-
ворота обойм от момента нагрузки М.
Для каждого из типов МСХ имеются [2, 3] свои зависимости = (М), которые весьма
сложны и не представляется возможным непосредственно вычислять жесткость C
o
МСХ.
Так при ведущей звездочке с плоской рабочей поверхностью угол относительного по-
ворота
зв
обойм определяется [3] на основе следующих выражений
)](sin)([sin
1111
c
R
, (1)
где
1
2
1
arccos
urR
urc
;
rR
rc
cos
;
rR
r
sin
arcsin
1
;
c
rR
arctg
sin)(
; R – ра-
диус отверстия обоймы; r – радиус ролика; с – расстояние по нормали от центра О звездочки до
плоской; – угол заклинивания, который обеспечивает условие заклинивания обойм; – угол
перемещения центра ролика; и
1
, и
2
– контактные деформации (сближения) в точках контакта ро-
лика с обоймой и звездочкой.
Если учитывать деформацию обоймы w, то в указанных выражениях вместо и
1
следу-
ет подставлять и
1
+ w = u
0
.
Все известные [2, 3] зависимости = (М) получены в рез ультате интегрирования ис-
ходных уравнений и поэтому получаются весьма сложными, а в некоторых случаях не могут
быть представлены в элементарных функциях.
Представляется возможным пол учить простые и обобщающие решения не производя
интегрирования. Так как и
0
<< (R – r); и
2
<< (c + r) и << , то разлагая в ряд одно и з выра-
жений системы (1)
