Сорокин А.А. Моделирование городских пассажирских перевозок
Подождите немного. Документ загружается.


Каждая
СМО
предназначена
для
обслуживания некоторого потока
заявок
(пассажиропоток), поступающих
на
вход
системы большей
частью
не
регулярно,
а в
случайные моменты времени. Обслуживание заявок,
в
общем
случае,
также длится
не
постоянное, заранее известное время,
а
случайное
время, которое зависит
от
многих причин (расстояние поездки пассажира).
После обслуживания заявки канал освобождается
и
готов
к
приему
следующей
заявки. Слз^айный характер потока заявок
и
времени
их
обслуживания приводит
к
неравномерной загруженности СМО:
в
некоторые
промежутки времени
на
входе
СМО
могут
скапливаться необслуженные
заявки
(час
пик),
что
приводит
к
перезагрузке СМО,
в
некоторые
же
другие
интервалы времени
на
входе
СМО заявок
не
будет
(межпик),
что
приводит
к
недозагрузке
СМО
(простаиванию канала обслуживания).
В
этой связи
необходима корректировка
в
интервалах движения транспортных единиц
по
марщруту,
для
обеспечения равномерной загрузки. Заявки,
скапливающиеся
на
входе
СМО, либо
«становятся»
в
очередь, либо
по
какой-
то причине невозможности дальнейщего пребывания
в
очереди покидают
СМО
необслуженными, например, превышение порогового значения времени
ожидания пассажиром начала обслуживания.
Приведем таблицу параметров (таблица
2.9) и
характеристики
проанализированной СМО.
Таблица
2.9
- Параметры многоканальной СМО
с
ожиданием без ограничения
на
длину очереди
и с
ограничением на время ожидания
в
очереди
п/п
1
2
3
4
5
6
7
Параметры
Число каналов обслуживания
Интенсивность
входящего простейшего потока Явх
Производительность каждого канала-
интенсивность простейшего потока обслуживании
Яоб каждым каналом (среднее число заявок,
обслуживаемых одним каналом
за
единицу времени
при
непрерывной его работе)
Максимальное число мест
в
очереди
Ограничение на время ожидания заявки
в
очереди
Среднее значение ограничения времени заявки
в
очепели
Интенсивность
простейшего потока
уходов
заявки
из
очереди
Пух
Обозначения, значения
п>1
1пЯвх
=
А,
=
const
(к
не зависит
от
времени)
тПо5 =
\i-
const
(ц
не зависит
от
времени)
7И=+00
Случайное время
Тож
Т
ож-ЩТож]
in/7yx=0)=
1/Гож
(о) не зависит от времени)
78

Характеристики функционирования многоканальной СМО с ожиданием
без ограничения на длину очереди и с ограничением на время ожидания
возможно представить в виде
следующих
формул:
1. Показатель (коэффициент) нагрузки СМО (трафик):
р=Х/ц.
i;i21)
2. Показатель (коэффициент) нагрузки, приходящейся на один канал:
\1/=р/п.
(2.23)
3. Приведенная интенсивность потока
уходов:
Р=(о/ц
(2.24)
4. Вероятность того, что все каналы свободны (вероятность простаивания
системы):
/'и „«00 _А-п ^~
5. Вероятность состояний:
Р'
f
.*
(2.26)
6. Среднее число заявок в очереди:
-я
00 /7, „Ч _*-П П-ТС
(2.27)
"' т "^
.е.(«+Ж«+2у^)*...*[«+(^-«)А]
J3
7. Среднее число заявок под обслуживанием (т.е. среднее число занятых
каналов):
V V
8. Среднее число заявок в системе:
— — —
Ncucm
= NoH
+
No6
=
(1
- fi)No4
+
p
9. Абсолютная пропускная способность:
А
=
Х-(о''тч
(2.30)
10. Относительная пропускная способность:
Q
=
AlX
=
\-{(olX)l^o4
(2.31)
11.
Вероятность того, что заявка
будет
обслужена:
79
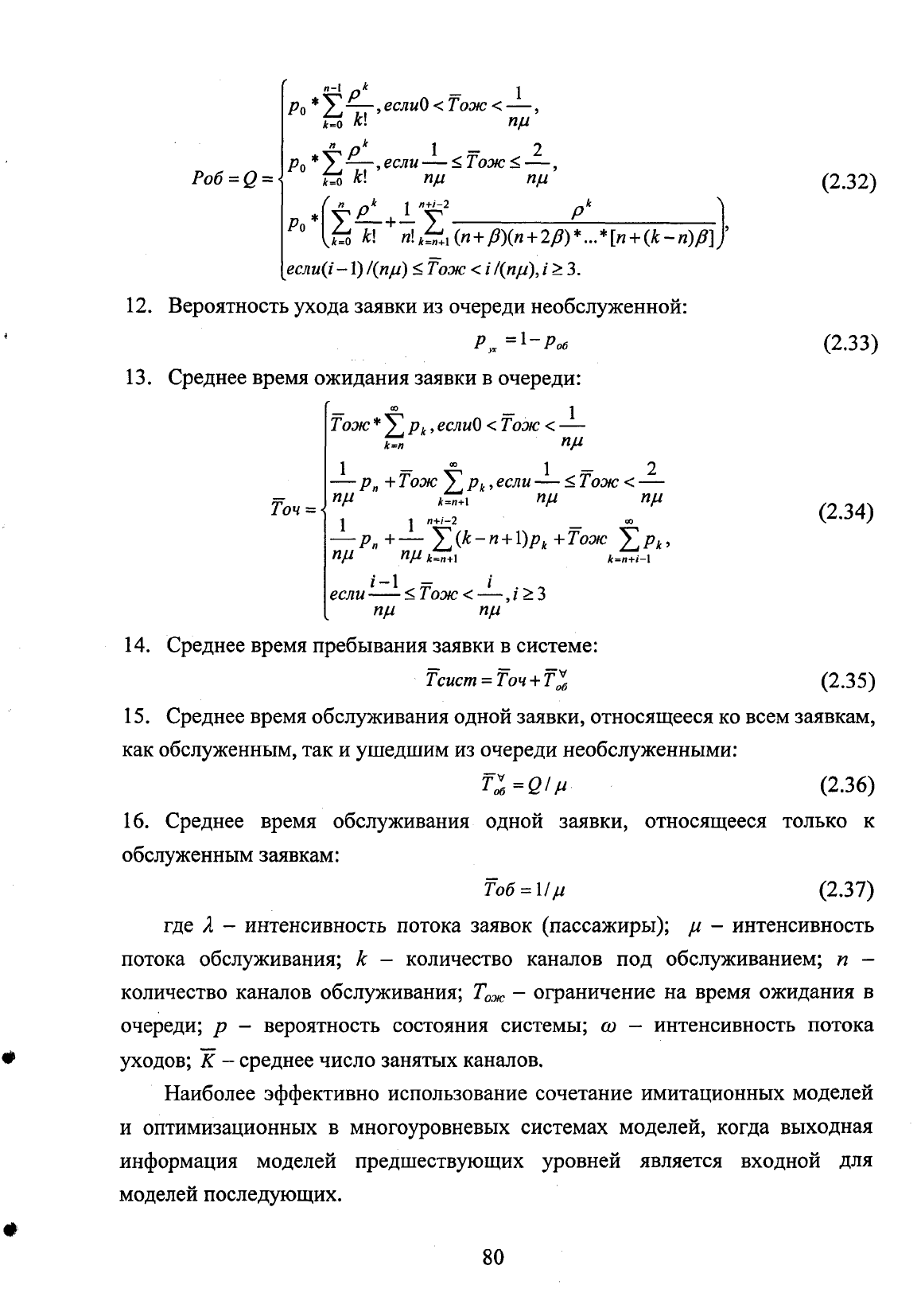
/—,еслиО
<
Тоэю
<
и//
По
А:!
^
•
_2_
(2.32)
если(1
-1)
/(«//)
<
Тож:
<
i
l{n^),
/
>
3.
12. Вероятность
ухода
заявки из очереди необс луженной:
(2.33)
13.
Среднее время ожидания заявки
в
очереди:
Тож
1
еслиО
< Тож
<
—
1
—
— р„
+
Тож
1 1 Л+/-2
1
— 2
—
-
Тож <
—
и//
п/л
(2.34)
если
<
Тоою
<
—,
/
> 3
пц
п/и
14. Среднее время пребывания заявки
в
системе:
Теист
=
foH
+
fl
(2.35)
15. Среднее время обслуживания одной
заявки,
относяш;ееся ко всем заявкам,
как
обслуженным, так
и
ушедшим из очереди необслуженными:
fl=QlM
(2.36)
16. Среднее время обслуживания одной заявки, относяш;ееся только
к
обслуженным заявкам:
To6
=
l/ju
(2.37)
где Л
-
интенсивность потока заявок (пассажиры);
// -
интенсивность
потока обслуживания;
к —
количество каналов
под
обслуживанием;
п —
количество каналов обслуживания;
Тож
—
ограничение
на
время ожидания
в
очереди;
р -
вероятность состояния системы;
со -
интенсивность потока
уходов;
К -
среднее число занятых каналов.
Наиболее эффективно использование сочетание имитационных моделей
и
оптимизационных
в
многоуровневых
системах
моделей, когда выходная
информация
моделей
предшествующих
уровней является входной
для
моделей
последующих.
80

2.3
Оптимизационные модели выбора иараметров системы с учетом
ограничений
на техннко-экономические и социальные показатели
Оптимизационные
модели
- это
самый объемный класс, который
наиболее широко представлен
в
современных исследованиях
в
области
моделирования систем пассажирского транспорта.
К ним
относятся модели
формирования
маршрутной сети
и ее
элементов, оптимального
взаимодействия участников рынка транспортных
услуг,
модели технико-
экономических
показателей.
Задача выбора схемы маршрутов пассажирского транспорта является
одной
из
важнейших
и
сложнейших среди задач, решаемых
в
процессе
организации
перевозок пассажиров.
От
того насколько удачно проложены
по
улицам города трассы маршрутов,
как они
увязаны
между
собой,
в
какой
степени маршруты удовлетворяют потребностям населения зависят
и
затраты
времени населения
на
передвижения,
и
показатели эффективности
использования
подвижного состава [20]. Основными исходными данными для
решения
вопросов организации маршрутной сети,
в
большинстве случаев,
служат
обраш;ения
и
предложения жителей города,
а так же
интуиция
работников пассажирского транспорта.
Первые работы
по
изучения
и
разработки методов формирования
схем
маршрутов пассажирского транспорта
в
нашей стране появились
в
начале
1930-х
гг.
[122-125].
Все
опубликованные методы определения
схем
маршру-
тов пассажирского транспорта можно разделить на две группы.
К
первой группе
следует
отнести работы, выполненные до 1963
года
[122-
127]. Основное внимание
в
этих работах уделялось установлению перечня
требований, предъявляемых
к
схемам маршрутов,
и
давались рекомендации
по
конфигурации маршрутов. Однако дать законченную методику выбора
схемы маршрутов для города, этим авторам не
удалось
из-за не достаточного
развития
в те
годы экономико-математических методов
и
отсутствия
быстродействуюш;их вычислительных машин.
Для
выбора схемы маршрутов
пассажирского транспорта этими авторами рекомендовалось использовать
данные
о
фактических передвижениях людей
по
городу.
В
этом
случае
появляется возможность создания такой схемы маршрутов пассажирского
транспорта, которая
в
максимальной степени удовлетворяла
бы
потребности
населения
в
передвижениях. Одной
из
целей, преследуемых
при
выборе
81

схемы маршрутов, является предоставление людям возможности совершения
своих передвижений по городу за минимальное время. Этого добиться, во-
первых, за счет выбора трасс маршрутов между конечными пунктами по
кратчайшему пути и, во-вторых, благодаря созданию такой комбинации
маршрутов, при которой общие затраты времени всех пассажиров на
передвижения
были бы минимальными.
При
решении задачи по выбору оптимального варианта схемы
автобусных маршрутов нельзя забывать и о необходимости рационального
использования
подвижного состава. Это требование может быть выражено
путем установления величины минимально допустимого коэффициента
динамического
использования вместимости подвижного состава на всех
маршрутах города [128]. В работе [129] предлагается установить предельную
минимальную
и максимальную длину маршрута. Л. Л. Поляков [130]
указывал на необходимость обеспечения рационального интервала движения
подвижного состава по маршруту. Эти требования можно учесть при решении
задачи путем задания допустимых пределов названных величин.
Ко
второй группе методов
следует
отнести работу "Методика
определения
оптимальной схемы автобусных маршрутов", выполненную в
1962-1963
гг. под руководством Б. Л. Геронимуса [128,131], а также
выполненную
в
1963-1966
гг. работу Д. Джумаева [132,133].
В этих работах были разработаны методики расчета схем маршрутов
пассажирского
транспорта в городах с использованием математических
методов. Был введен критерий оптимальности схемы автобусных маршрутов
для города, разработан вариант математической постановки задачи выбора
оптимальной
схемы автобусных маршрутов для города может быть решена
только методами комбинаторного анализа, то есть путем сравнения между
собой
всех вариантов маршрутных схем.
В работе [20] произведена доработка методики расчета маршрутных схем.
Автор
применяет два понятия общая и локальная маршрутизация, под
которыми
понимается формирование маршрутной сети в целом (при обшей) и
формирование
отдельных элементов: отдельных маршрутов (основной и
укороченный),
остановочных пунктов (при локальной).
Автор
формулирует задачу следующим образом: каждый вариант схемы
маршрутов характеризуется определенными показателями, для расчет
которых необходимо: установить трассы возможных маршрутов, выбрать
82

пути следования пассажиров
между
всеми пунктами города, распределить
пассажирские потоки
между
маршрутами, определить
частоту
движения
транспорта по каждому маршруту, определить необходимое для работы на
каждом маршруте количество транспорта, рассчитать затраты времени
пассажиров на следование и пересадки, вычислить затраты времени
пассажиров на ожидание начала поездки по каждому маршруту и по каждому
участку
маршрутной сети и рассчитать ряд показателей, характеризуюших
каждый отдельный маршрут и всю совокупность маршрутов в целом. Расчёты
для каждого рассматриваемого варианта схемы маршрутов проводятся в
отдельности. Цель решения задачи - выбрать такой вариант схемы
маршрутов, который наилучшим образом соответствовал бы заданному
критерию оптимальности.
Для решения задачи используются как данные, которые можно получить
только на основе специальных обследований, так и данные, имеюш;иеся в
муниципалитетах и транспортных организациях.
Известна
транспортная сеть города, состоящая из узлов (центров
микрорайонов)
и ребер (улиц, по которым организовано или возможно
движение пассажирского транспорта), соединяющих узлы
между
собой.
Каждому
узлу
транспортной сети соответствует величина
tnw,
численно равная
затратам времени на пересадку в пункте
W.
Каждому ребру сети соответствует
величина tdj численно равная затратам времени на движение автобуса
между
пунктами /
и
j.
Известно расстояние
между
пунктами / иу - длина ребра
Ljy
В
общем
случае
tcijфtcji
и
Lij^Lji.
Задана матрица корреспонденции (количество
передвижений населения)
между
всеми микрорайонами города за
определенный (расчётный) период суток -ПК II, где элемент Щ -
соответствует числу передвижений, совершаемых из пункта / в пункту. Каж-
дой комбинации маршрутов, соединяющих
между
собой узлы транспортной
сети, соответствует величина Е, численно равная суммарным затратам
времени
всех
пассажиров на передвижения по всем маршрутам, включая
затраты времени на ожидание начала поездки, следование в подвижном
составе и пересадки с маршрута на маршрут,
В качестве критерия оптимальности схемы марщрутов принимается
минимум суммарных затрат времени населения на передвижения с
использованием транспорта, включая оцененные временем неудобства.
83

испытываемые пассажирами при совершепии пересадок
и
денежные затраты
на
покупку билета на проезд.
В процессе решения задачи
требуется
минимизировать функционал Е:
-.v
-^v
(2.38)
<=1
j=\ k=l v=r
где
/
=
l,2,...,m
- пункты (микрорайоны) начала передвижений;
У
=
1,2,..
.,w
-
пункты (микрорайоны) окончания передвижений;
к=\,1,...,п-маршруты автобусов;
V
=
1,2,...
,w
-
совмеш;енные участки транспортной сети;
tdj,
tnij
-
затраты времени одного пассажира при проезде
между
пунктами
/
и
j,
соответственно, на следование и пересадки;
Kij
-
число передвижений
между
пунктами
/
иу;
toж,k
-
затраты времени одного пассажира
на
ожидание начала поездки
по
- число пассажиров, пользуюпщхся только маршрутом к,
.v
-
затраты времени одного пассажира
на
ожидание начала поездки
при
проезде по совмеш,енному
участку
транспортной сети V;
Ру
-
число пассажиров, проезжаюпщх
по
совмещенному
участку
V.
Между
пунктами i иу организация маршрута запрещается, если
^ij
'-'min
^у
^тах
i€Mo
(2.39)
j€Mo
где
Ly
-
протяженность маршрута
между
пунктами i иу км;
L^rc-
максимально допустимая протяженность маршрута, км;
Lmin
-
минимально допустимая протяженность маршрута, км;
1у
-
интервал движения
автобусов
по
маршруту
между
пунктами
/
иу,
мин;
Imax
-
максимально возможный интервал движения
автобусов
по
маршруту,
мин;
ij
-
конечные пункты маршрута;
Мо
-
множество
узлов
(микрорайонов города), закрытых
для
организации
конечных пунктов маршрутов;
84

-
множество
запрещенных
маршрутов,
заданных в исходных данных;
Ку, Kji - количество передвижений
между
микрорайонами / иу в прямом и
обратном направлениях;
Пщ1п
- минимальное и необходимое для открытия маршрута (необходимое
условие) количество пассажиров, проезжающих
между
конечными пунктами
маршрута.
Все ограничения задаются в исходных данных.
Общее количество автобусов
{Аов),
необходимое для работы на
всех
маршр5п:ах города, определяется по формуле:
^06=
Ел
(2.40)
где
Ak
- количество автобусов, необходимое для работы на маршруте к.
В случае, если при очередном рассматриваемом варианте схемы
маршрутов
Аоб^Аз,
где Аз
-
количество автобусов, выделяемых транспортными
предприятиями
для работы на
всех
маршрутах города, то рассчитывается
скорректированное
(с
учетом
имеющихся возможностей) количество
автобусов для работы на к-ом маршруте по формуле:
Ак..ор=Ак-(А/Аоб)
(2.41)
где
А/скор
- количество автобусов, выделяемых для работы на маршруте
к,
с
учетом
имеющегося в городе парка подвижного состава.
Для осуществления расчётов по выбору оптимальной схемы автобусных
маршрутов необходимы следующие исходные данные.
1. Схема транспортной сети города.
2. Протяженность участков транспортной сети города и время движения
автобусов по каждому из них.
3. Затраты времени на пересадку пассажира с маршрута на маршрут.
4. Таблица корреспонденции населения
между
микрорайонами города с
использованием
транспорта. Корреспонденции населения
между
микрорайонами
города являются основными исходными данными,
используемыми при проведении расчётов по выбору оптимальной
схемы автобусных маршрутов. В связи с этим
следует
стремиться к
максимальной
их адекватности с реальными передвижениями жителей
по
городу.
Так как данные о передвижениях жителей
между
микрорайонами
города можно получить для любого периода суток, то
для расчета схемы маршрутов
следует
выбрать период суток со
85

стабильным и максимальным числом передвижений. Таким периодом
может быть один час, либо весь период утренних или вечерних часов
пик.
В целях получения данных о стабильных пассажирских потоках
изучение передвижений населения по
городу
целесообразно проводить
в
будний день зимнего периода времени,
5. Средняя вместимость автобуса. Эта величина (q) может быть задана
эмпирически
или определена расчетным путем по формуле:
^
=
{tb-^f\tAf
(2.42)
где/=
1,2,...,и-
типы автобусов, используемых в городе;
qf- вместимость автобуса/-го типа;
Af- число автобусов/-го типа.
6.
Коэффициент
внутри часовой неравномерности пассажирского потока;
7. Продолжительность расчетного периода времени, то есть периода для
которого определены данные о корреспонденциях населения
между
микрорайонами
города.
8.
Коэффициент
неравномерности подхода пассажиров к остановке.
9. Ограничения, учитываемые при выборе оптимального варианта схемы
автобусных маршрутов.
В число ограничений входят:
• минимально допустимый коэффициент использования вместимости
автобусов;
• минимально и максимально возможные протяженности маршрута;
• максимально возможное число автобусов для работы на маршрутах;
• перечень микрорайонов, в которых, по условиям движения
транспорта в городе, невозможна организация конечных пунктов
маршрутов;
• перечень маршрзо-ов, обязательно включаемых в оптимальный
вариант схемы автобусных маршрутов (в состав заданных маршрутов
включаются те автобусные маршруты, которые по каким-либо
причинам
должны обязательно войти в окончательный вариант
схемы, а также маршруты электротранспорта);
• перечень запрещенных маршрутов;
86

• минимальное число пассажиров, проезжающих
между
конечными
пунктами маршрута, принимаемое в качестве условия, необходимого
для принятия решения об открытии маршрута.
Решение
задачи начинается с установления перечня возможных маршрутов
автобусов.
Недостатком данной модели является выбор
схемы
маршрутов для одного
вида пассажирского транспорта - автобусного. В данной модели так же не
учитывает
возможность взаимодействия
двух
видов подвижного состава в
пределах
одного маршрута.
Главной задачей планирования функционирования системы ГПТ является
прогнозирование и формирование заданного уровня сервиса пассажирских
услуг
с минимальными издержками на их реализацию. Это позволяет при
экономически
обоснованных тарифах получить максимальную прибыль от
работы транспорта. Учитывая его
особую
социальную значимость для
населения
города, можно установить фактические тарифы ниже расчетных,
минимизировать
размер дотации на поддержание заданного уровня сервиса.
Для построения модели выбора стратегии достижения оптимального
уровня сервиса пассажирских
услуг
используем формализованное
условие
идеально функционирующей системы ГПТ с точки зрения ее качества [52].
Известен
уровень сервиса пассажирских
услуг
где
6*^
- q-й показатель уровня сервиса пассажирских
услуг.
Известны
и определены зависимости затрат Сд от каждого показателя Sqj
C,=C(,)+C,(,)/{\-S,),
Q=\,p
(2.43)
где C(q) - условно-постоянная составляющая затрат, не зависящая от
показателя
Sq;
Ci(q)
- условно-переменная составляющая затрат, зависящая от показателя
Sq.
Очевидно, что общие затраты по обеспечению заданного уровня сервиса
пассажирских
услуг
будут
равны:
q-l
87
