Сорокин А.А. Моделирование городских пассажирских перевозок

Подождите немного. Документ загружается.

обязаны

даже

быть случайными величинами и

метод

является линейным и

аддитивным. Несмотря на то, что при

методе

главных компонент для точного

воспроизведения коэффициентов корреляции

между

переменными надо найти

все («) компонент, большая доля изменчивости признаков (дисперсии)

объясняется небольшим числом (т) компонент. Кроме того, при

методе

главных компонент можно по признакам описать компоненты, а по

компонентам признаки [62].

Порой

объект исследования характеризуется набором числовых данных,

изменяюшихся во времени. Числовые данные, характеризующие процессы,

находящиеся в постоянном изменении и движении,

образуют

ряды динамики

(временные ряды). Чаще всего под динамическими рядами понимается

хронологические (или временные) последовательности,

хотя

в принципе

выражение "динамика"

охватывает

не только изменение во времени, но и

любое

другое

изменение состояния под влиянием внешних условий.

Под динамическим (временным) рядом

будем

понимать

последовательность наблюдений некоторого признака (случайной величины)

в последовательные моменты времени. Отдельные наблюдения называются

уровнями ряда и обозначаются Y,{t= 1,2,

...,п),

где п - число уровней.

Теоретической базой для анализа динамических рядов явилась теория

случайных процессов [71,72]. Случайные процессы представляют собой

семейство случайных функций X{t), зависящих от одного параметра, которым

в большинстве

случаев

является время.

Как

показывает большинство работ

[57,58,69-72]

временной ряд

формируется под воздействием закономерной и случайной составляющих.

Закономерные изменения членов временного ряда

следуют

какому-то

определенному правилу, и их влияние может быть устойчивым в течение

достаточно длительных промежутков времени. Это обеспечивает возможность

прогноза для подобных временных рядов. Если полностью выявить

закономерную составляющую в поведении временного ряда, то оставшаяся

часть выглядит хаотично и непредсказуемо. Ее обычно именуют

иррегулярной, или случайной компонентой временного ряда. Анализ

случайной компоненты можно использовать для вычисления вероятных

ошибок и оценки надежности примененной модели прогнозирования.

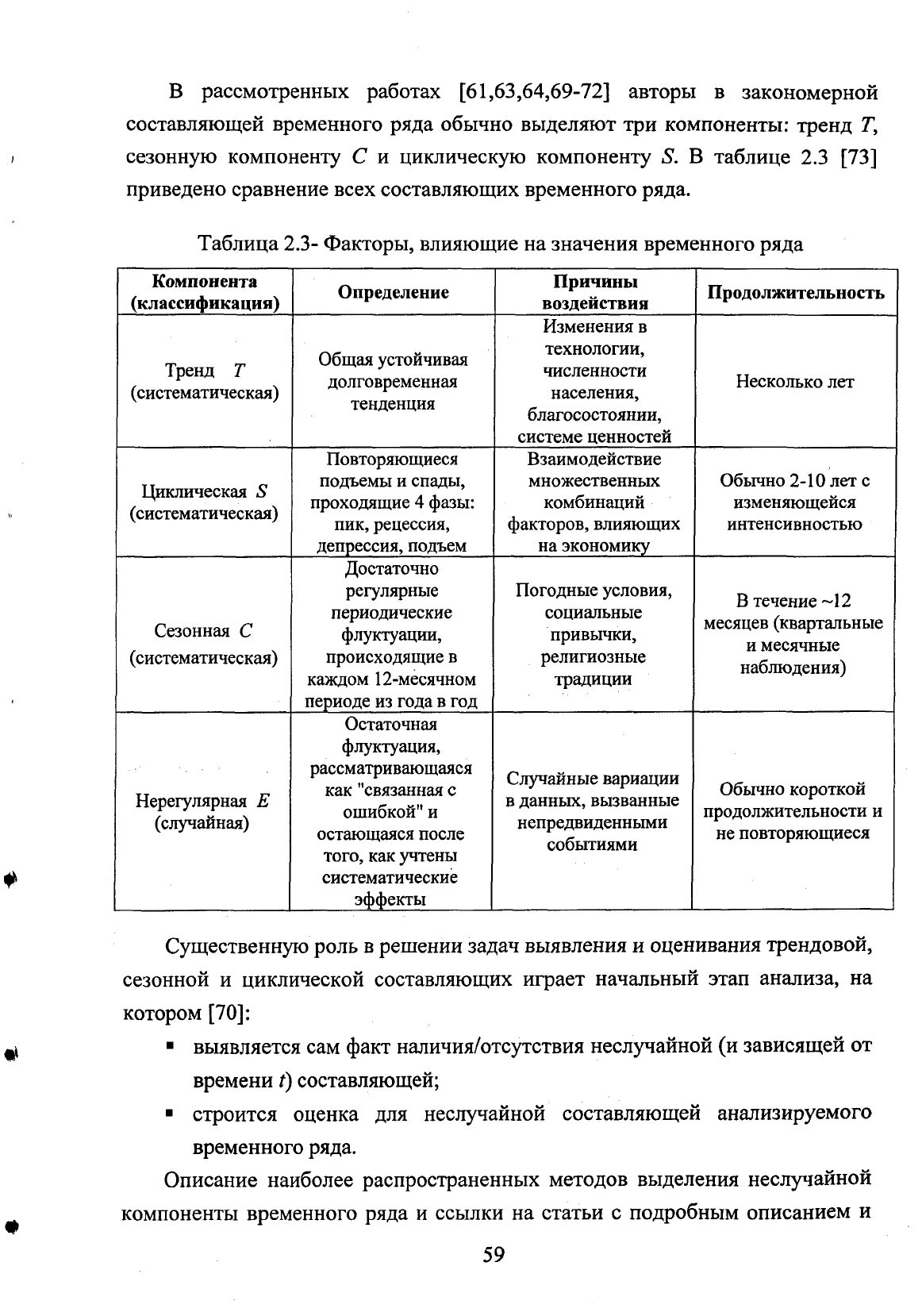
в рассмотренных

работах

[61,63,64,69-72]

авторы

закономерной

составляющей временного ряда обычно

выделяют

три

компоненты:

тренд

7",

сезонную компоненту

С и

циклическую компоненту

S. В

таблице

2.3 [73]

приведено сравнение

всех

составляющих временного ряда.

Таблица 2.3- Факторы, влияющие на значения временного ряда

Компонента

(классификация)

Тренд

(систематическая)

Циклическая

(систематическая)

Сезониая

(систематическая)

•.

• •

Нерегулярная

(случайная)

Определение

Общая устойчивая

долговременная

тенденция

Повторяющиеся

подъемы и снады,

нроходящие

фазы:

пик,

рецессия,

депрессия, подъем

Достаточно

регулярные

периодические

флуктуации,

происходящие

каждом 12-месячном

периоде из

года

в год

Остаточная

флуктуация,

рассматривающаяся

как

"связанная

ощибкой"

остающаяся после

того, как

учтены

систематические

эффекты

Причииы

воздействия

Изменения

технологии,

численности

населения,

благосостоянии,

системе ценностей

Взаимодействие

множественных

комбинаций

факторов,

влияющих

на

экономику

Погодные условия,

социальные

привьики,

религиозные

традиции

Случайные вариации

данпъ1х,

вызванные

непредвиденными

событиями

Продолжительиость

Несколько

лет

Обычно

2-10 лет с

изменяющейся

интенсивностью

В течение

~12

месяцев (квартальные

месячные

наблюдения)

Обычно короткой

продолжительности

не

повторяющиеся

Существенную

роль

решении

задач

выявления

оценивания трендовой,

сезонной

циклической составляющих

играет

начальный этап анализа,

на

котором

[70]:

• выявляется сам факт наличия/отсутствия неслучайной (и зависящей

от

времени

составляющей;

• строится оценка

для

неслучайной составляющей анализируемого

временного ряда.

Описание наиболее распространенных

методов

выделения неслучайной

компоненты временного ряда

ссылки

на

статьи

подробным описанием

теоретическим обоснованием этих методов можно найти, например, в

работах

[57,76-78,84-89].

При этом методы выделения неслучайной составляющей в

траектории, отражающей поведение временного ряда, подразделяются на два

типа:

1. Методы первого типа (аналитические) основаны на допущении, что

известен общий вид неслучайной составляющей

¥{г)

Ххт

Х2т+хЛ1).

(2.8)

2. Методы второго типа (алгоритмические) не связаны ограничительным

допущением о том, что общий аналитический вид искомой функции известен

исследователю. В этом смысле они являются более гибкими, более

привлекательными. Однако «на

выходе»

задачи они

предлагают

исследователю лишь алгоритм расчета оценки для искомой функции Y{t) в

любой наперед заданной точке / и не

претендуют

на аналитическое

представление функции.

Более предсказуемы такие составляющие объема перевозок как

подвижность населения и его численность, исследуя которые с

использованием трендовых моделей, можно расчетным

путем

получить

прогноз общего объема перевозок по всем видам пассажирского транспорта.

Поскольку объем перевозок определяется, в

первую

очередь, численностью

населения

города, его подвижностью, а также параметрами маршрутной сети.

В таблице 2.4 представлена динамика изменения численности населения,

подвижности и объема перевозок пассажиров ГПТ за период с 1980 по

2003

год.

Одной из основных

задач

исследования временного ряда является выяв-

ление основной тенденции изучаемого процесса, выраженной неслучайной со-

ставляющей Т

тренда.

Поскольку действие экономических, социальных, технологических и им

подобных факторов происходит

постепенно,

их вклад в тенденцию ряда иссле-

дователи предпочитают описывать с помощью гладких кривых, просто задаю-

щихся в аналитическом виде. В данном

случае

следует

использовать способ

аналитического выравнивания. При таком

подходе

аналитическое выравнива-

ние

есть не что

иное,

как удобный способ описания эмпирических данных.

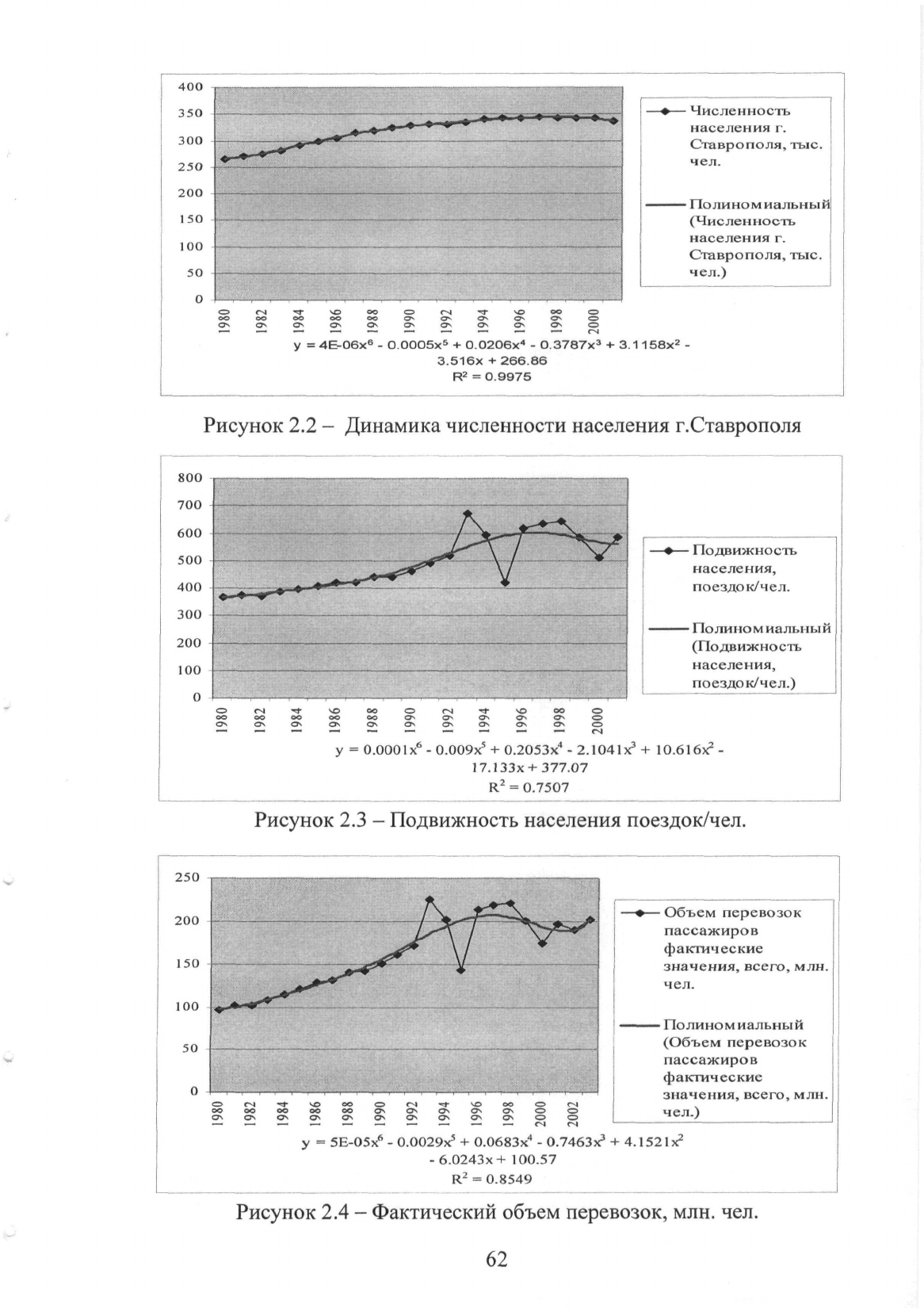
Для более наглядного представления представим исходные данные в виде

графиков

(рисунки

2.2-2.4).

В качестве аппроксимирующих были выбраны

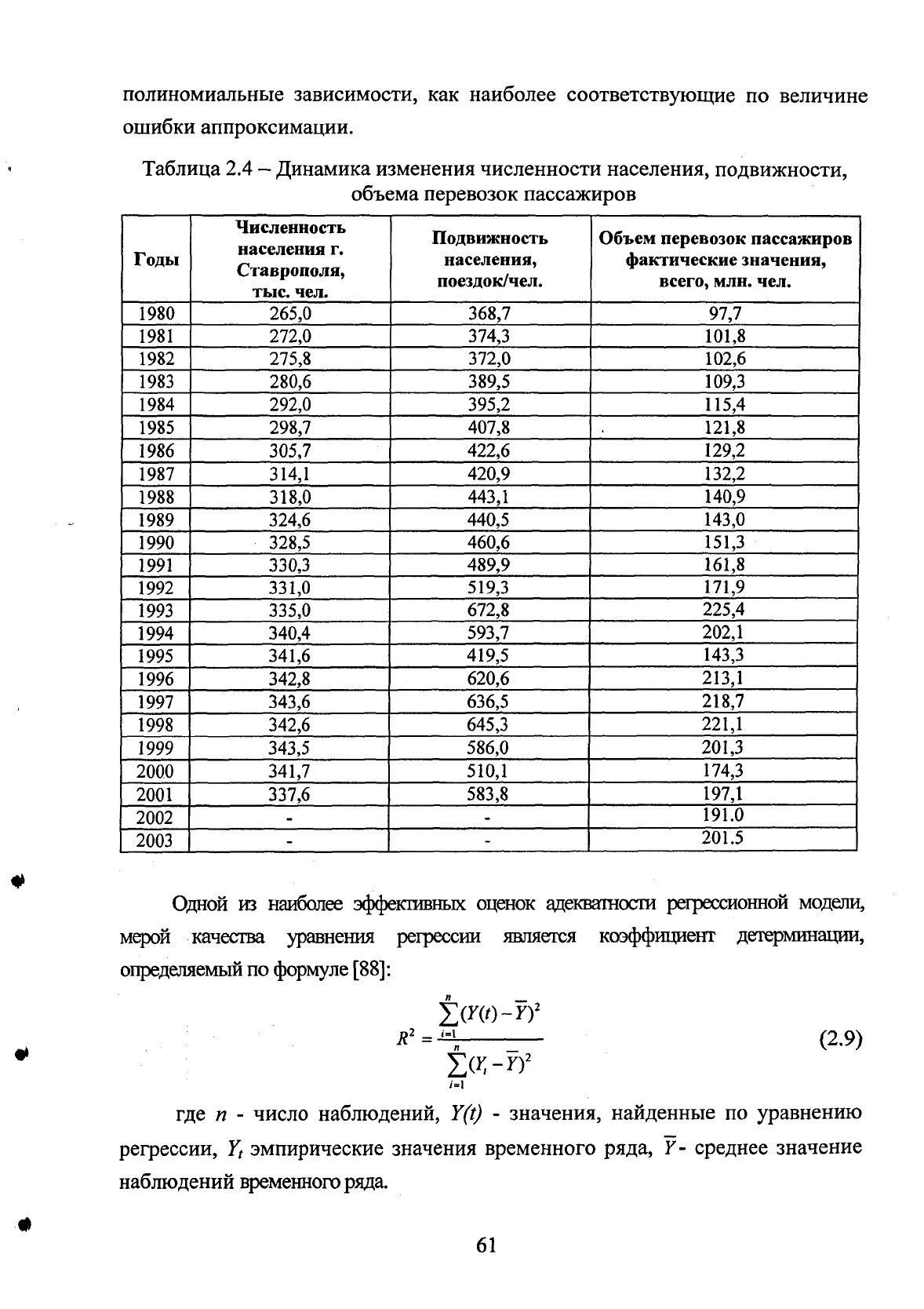
полиномиальные зависимости, как наиболее соответствующие по величине

ошибки аппроксимации.

Таблица 2.4

—

Динамика изменения численности населения, подвижности,

объема перевозок пассажиров

Годы

1980

1981

1982

1983

1984

1985

1986

1987

1988

1989

1990

1991

1992

1993

1994

1995

1996

1997

1998

1999

2000

2001

2002

2003

Численность

населення

г.

Ставрополя,

тыс. чел.

265,0

272,0

275,8

280,6

292,0

298,7

305,7

314,1

318,0

324,6

328,5

330,3

331,0

335,0

340,4

341,6

342,8

343,6

342,6

343,5

341,7

337,6

Подвнжность

населення,

ноездок/чел.

368,7

374,3

372,0

389,5

395,2

407,8

422,6

420,9

443,1

440,5

460,6

489,9

519,3

672,8

593,7

419,5

620,6

636,5

645,3

586,0

510,1

583,8

Объем неревозок нассажнров

фактнческне

значення,

всего, млн. чел.

97,7

101,8

102,6

109,3

115,4

121,8

129,2

132,2

140,9

143,0

151,3

161,8

171,9

225,4

202,1

143,3

213,1

218,7

221,1

201,3

174,3

197,1

191.0

201.5

Одной из наиболее эффекшвных оценок адеквагаосш регрессионной модели,

мерой качества уравнения регрессии является коэффициент детерминации,

определяемый

по

формуле [88]:

(2.9)

где n - число наблюдений, Y(t) - значения, найденные по уравнению

регрессии. Г, эмпирические значения временного ряда, Y- среднее значение

наблюдений временного ряда.

400 -|

350

300

250

200

150

1980

.j||L-,

1982

1984

1986

1988

4Е-06хв -

---

пч -^

ON ON

О^

^^ ON

ЧО

Оч

0.0005Х* + О.ОгОбх"

- 0

3.516Х

R2 =

266.86

9975

—.

• •-

—-,

—

ооог

8661

—ф—

Численность

населения г.

Ставрополя, тыс.

чел.

Полином

иальный

(Численность

населения

г.

Ставрополя, тыс.

чел.)

.3787x3

3.1158x2 -

Рисунок

2.2

Динамика численности населения г.Ставроноля

800

700

600

500

400

300

200

100

ОО

Подвижность

населения,

поездок/чел.

-Полиномиальный

(Подвижность

населения,

поездок/чел.)

0.000

lx"^

- 0.009х'

О.гОЗЗх"

- 2.1041Х* + 10

17.133Х+377.07

R^ =

0.7507

Рисунок

2.3

Подвижность населения ноездок/чел.

250

200

150

100

-Объем

перевозок

пассажиров

фактические

значения,

всего, млн.

чел.

•Полиномиальный

(Объем

перевозок

пассажиров

фактические

значения,

всего, млн.

чел.)

0.7463х'

-6.0243Х+

100.57

R^ =

0.8549

Рисунок

2.4

Фактический

объем

перевозок, млн.

чел.

Коэффициент

детерминации принимает значение от

до 1: чем ближе его

значение к 1, тем в большей степени учтены факторы, влияющие на зависимую

переменную, тем более точной может быть модель. Сила связи зависимой пе-

ременной и времени в зависимости от коэффициента детерминации представ-

лена в таблице 2.5 [101].

Таблица 2.5 - Сила связи зависимой и независимой переменных в зависимости

от

коэффициента

детерминации

Коэффициент

детерминации

От

±0,81

до ±1,00

От

±0,61

до ±0,80

От

±0,41

до ±0,60

От

±0,21

до ±0,40

От ±0,00 до ±0,20

Сила связи

Сильная

Умеренная

Слабая

Очень слабая

Отсутствует

В прогнозных расчетах по уравнению регрессии определяется

предсказываемое значение

Ynpor

путем подстановки в уравнение регрессии

Y(X1) соответствующего значения XI „рог- Однако точечный прогноз

Y(Xlnpor)

дополняется расчетом стандартной ошибки AY.

Стандартная ошибка предсказываемого среднего значения определяется

по

формуле [108]:

(2.10)

где

S-

остаточная дисперсия на одну степень свободы. Х- значения фактора, X

среднее значение фактора.

Данная формула стандартной ошибки предсказываемого среднего значения

^прог

При заданном значении

XI„рог

характеризует ошибку положения линии

регрессии.

Для прогнозируемого значения 95%-ные доверительные интервалы при

заданном

XI„рог

определяются выражением

Y(X\^p^J±t-AY,

где t - ^-критерий

Стьюдента, определяемый при уровне значимости а = 0.05 и числе степеней

свободы (и-2).

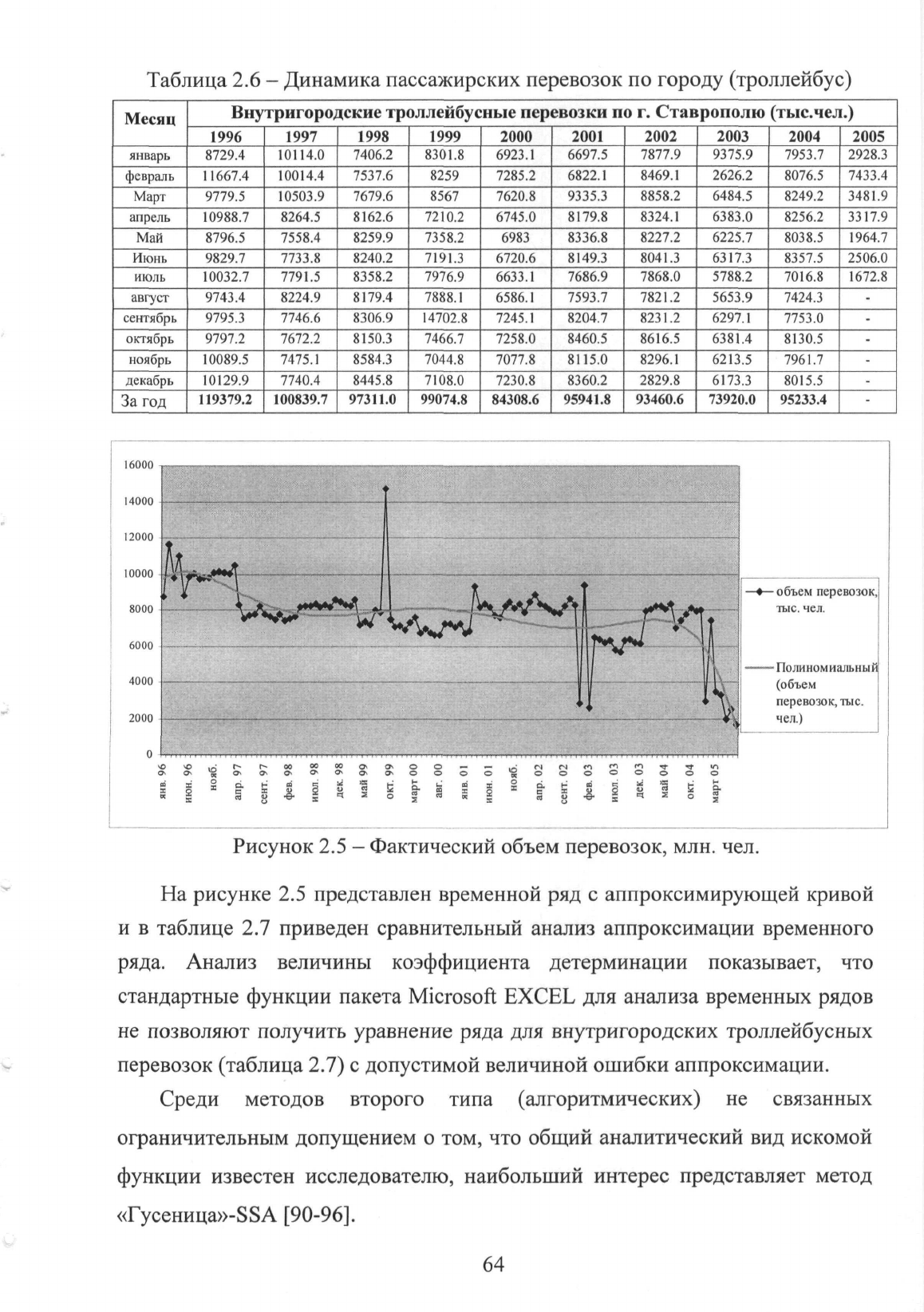
В таблице 2.6 представлена динамика пассажирских перевозок

троллейбусами по г. Ставрополю с 1996 по

2005

годы.

Таблица

2.6

Месяц

январь

февраль

Март

апрель

Май

Июнь

июль

август

сентябрь

октябрь

ноябрь

декабрь

За

год

Динамика

пассажирских

перевозок

ПО

городу (троллейбус)

Внутригородские

троллейбусные

иеревозки

по

г.

Ставрополю

(тыс.чел.)

1996

8729.4

11667.4

9779.5

10988.7

8796.5

9829.7

10032.7

9743.4

9795.3

9797.2

10089.5

10129.9

119379.2

1997

10114.0

10014.4

10503.9

8264.5

7558.4

7733.8

7791.5

8224.9

7746.6

7672.2

7475.1

7740.4

100839.7

1998

7406.2

7537.6

1619.6

8162.6

8259.9

8240.2

8358.2

8179.4

8306.9

8150.3

8584.3

8445.8

97311.0

1999

8301.8

8259

8567

7210.2

7358.2

7191.3

7976.9

7888.1

14702.8

7466.7

7044.8

7108.0

99074.8

2000

6923.1

7285.2

7620.8

6745.0

6983

6720.6

6633.1

6586.1

7245.1

7258.0

7077.8

7230.8

84308.6

2001

6697.5

6822.1

9335.3

8179.8

8336.8

8149.3

7686.9

7593.7

8204.7

8460.5

8115.0

8360.2

95941.8

2002

7877.9

8469.1

8858.2

8324.1

8227.2

8041.3

7868.0

7821.2

8231.2

8616.5

8296.1

2829.8

93460.6

2003

9375.9

2626.2

6484.5

6383.0

6225.7

6317.3

5788.2

5653.9

6297.1

6381.4

6213.5

6173.3

73920.0

2004

7953.7

8076.5

8249.2

8256.2

8038.5

8357.5

7016.8

7424.3

7753.0

8130.5

7961.7

8015.5

95233.4

2005

2928.3

7433.4

3481.9

3317.9

1964.7

2506.0

1672.8

объем

перевозок,

тыс.

чел.

Полиномиальный

(объем

перевозок,

тыс.

чел.)

— —

Рисунок

2.5 -

Фактический

объем

перевозок,

млн.

чел.

На

рисунке 2.5 представлен

временной

ряд с

аппроксимирующей

кривой

в таблице 2.7 приведен

сравнительный

анализ

аппроксимации

временного

ряда.

Анализ величины

коэффициента

детерминации показывает, что

стандартные

функции

пакета Microsoft EXCEL для анализа

временных

рядов

не

позволяют получить уравнение ряда для внутригородских троллейбусных

перевозок

(таблица

2.7) с

допустимой

величиной

ошибки

аппроксимации.

Среди

методов второго типа (алгоритмических) не связанных

ограничительным

допущением

о том, что

общий

аналитический

вид

искомой

функции

известен исследователю,

наибольший

интерес представляет метод

«Гусеница»-88А [90-96].

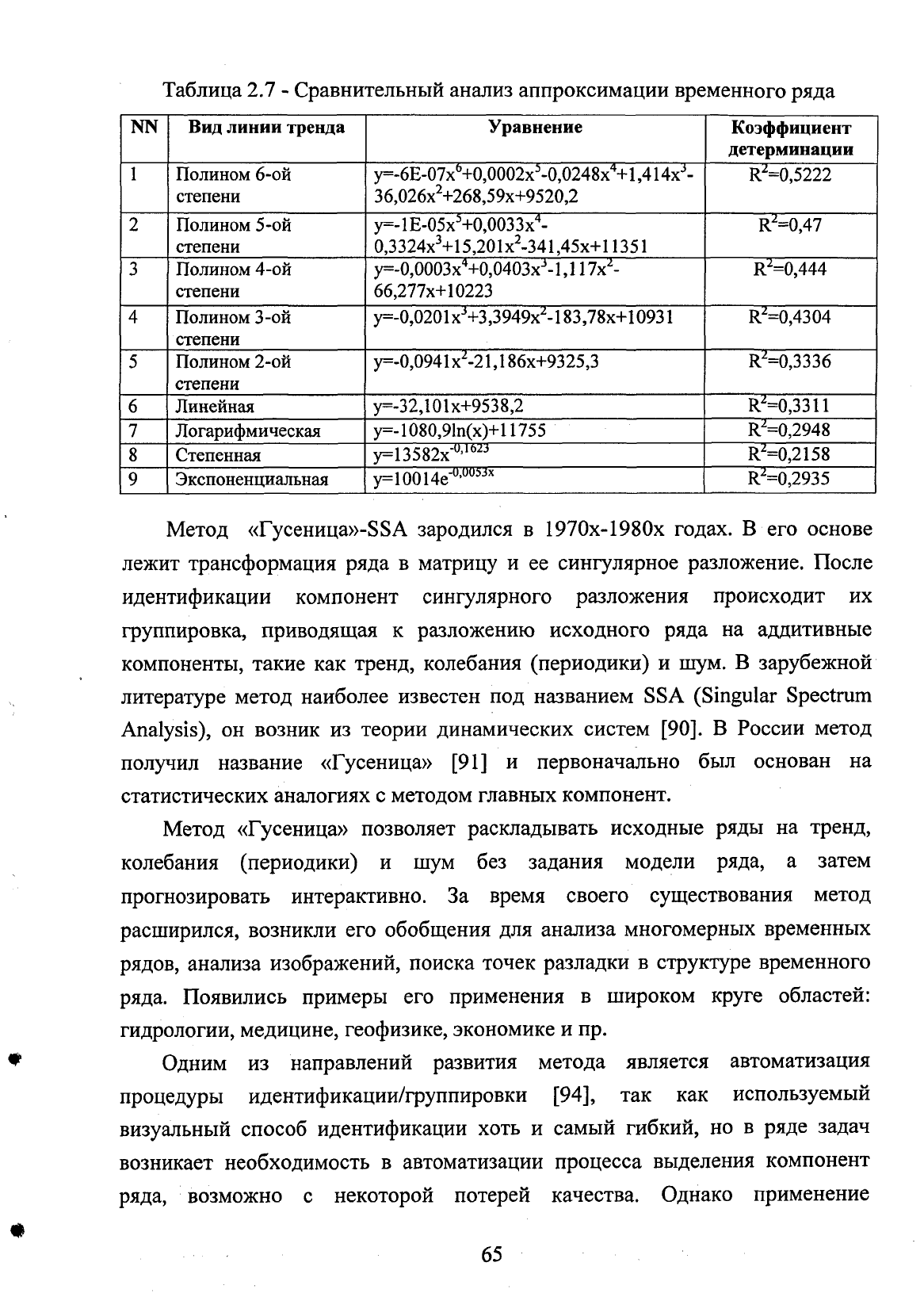
Таблица 2,7 - Сравнительный анализ аппроксимации временного ряда

Вид

линии

тренда

Полином

6-ой

степени

Полином

5-ой

степени

Полином

4-ой

степени

Полином

3-ой

степени

Полином

2-ой

степени

Линейная

Логарифмическая

Степенная

Экспоненциальная

Уравнение

у=-6Е-07х''+0,0002х'-0,0248хЧ1,4

Их-"-

36,026х^+268,59х+9520,2

у=-1Е-05хЧ0,0033х^-

0,3324х^+15,201х^-341,45х+11351

у=-0,0003хЧ0,0403х^-1,117х^-

66,277х+10223

у=-0,0201хЧз,3949х^-183,78х+10931

у=-0,0941

х^-21,186Х+93

25,3

у=-32,101х+9538,2

у=-1080,91п(х)+11755

у=13582х-"'''''

у=10014е-"'"""''

Коэффициент

детерминации

R^=0,5222

R^=0,47

R^=0,444

R^=0,4304

R^=0,3336

R^=0,3311

R^=0,2948

R^=0,2158

R^=0,2935

Метод

«Гусеница»-88А

зародился в

1970х-1980х

годах.

В его основе

лежит трансформация ряда в матрицу и ее сингулярное разложение. После

идентификации

компонент сингулярного разложения происходит их

группировка, приводящая к разложению исходного ряда на аддитивные

компоненты,

такие как тренд, колебания (периодики) и шум. В зарубежной

литературе метод наиболее известен под названием SSA (Singular Spectrum

Analysis),

он возник из теории динамических систем [90]. В России метод

получил название

«Гусеница»

[91] и первоначально был основан на

статистических аналогиях с методом главных компонент.

Метод

«Гусеница»

позволяет раскладывать исходные ряды на тренд,

колебания

(периодики) и шум без задания модели ряда, а затем

прогнозировать интерактивно. За время своего суш;ествования метод

расширился,

возникли его обобщения для анализа многомерных временных

рядов, анализа изображений, поиска точек разладки в

структуре

временного

ряда. Появились примеры его применения в широком круге областей:

гидрологии, медицине, геофизике, экономике и пр.

Одним из направлений развития метода является автоматизация

процедуры идентификации/группировки [94], так как используемый

визуальный способ идентификации

хоть

и самый гибкий, но в ряде задач

возникает необходимость в автоматизации процесса выделения компонент

ряда, возможно с некоторой потерей качества. Однако применение

автоматических методов переносит проблему с задачи интерактивной

идентификации

на

задачу

интерактивного выбора параметров.

Первой

идеей, лежащей в основе метода, является создание повторности

путем перехода от временного ряда (последовательности некоторых

измерений

или характеристик в равноотстоящие моменты времени) к

последовательности векторов, состоящих из отрезков временного ряда

выбранной

длины. Таким образом, получается что-то вроде многомерной

выборки,

так как если исходный ряд имел какую-то

структуру,

то и его

отрезки наследуют эту

структуру.

Второй идеей является анализ полученной

многомерной выборки (траекторной матрицы) с помощью ее сингулярного

разложения или, используя статистические аналогии, анализа главных

компонент.

Тем самым получается разложение исходного временного ряда

(точнее, его траекторной матрицы) по базису, порождаемому им самим.

Алгоритм метода

«Гусеница»-88А

подробно он описан в работах [92,96].

Краткое

описание алгоритма заключается в рассмотрении вещественно-

значного временного ряд

F^^

=(/o,-.-./v-i) длины Л'^, N>2.

Алгоритм можно разбить на четыре шага: вложение, сингулярное

разложение, группировка и диагональное усреднение. Первые два в

совокупности называются разложением, последние - восстановлением.

Основным

параметром алгоритма служит, так называемая длина окна I,

\<L<N.

Результатом алгоритма является разбиение временного ряда на

аддитивные составляющие.

Разложение.

Первый шаг, вложение, состоит в формировании из ряда

траекторной матрицы X размером LxK, K

N~L

следующим образом.

Последовательно берутся из ряда отрезки длины L и составляется из них

траекторная матрица Х

[^, :...:Х^^], где Х^

=(/,_,,...,/y+^,_2)

. Далее

проводится сингулярное разложение матрицы X:

где

Д,

>Я2 ^...^/Ij >0 - упорядоченные ненулевые собственные числа

матрицы ХХ^,

{f/,}ti:

t/, е R^ - соответствующие им собственные вектора, а

: ^

>^Г"^Х^[/,

е R^ называются факторными векторами.

Восстановление.

На

третьем

шаге проводится группировка компонент

разложения.

Разбив

{\,...,d}

на т непересекающихся подмножеств Ij,

получим

Последним

шагом является восстановление рядов F^^ по

сгруппированным матрицам Ху . Элемент ряда f^^ получается с помош;ью

усреднения вдоль антидиагонали элементов матрицы X;. с индексами а и Ь

такими,

что

Таким образом, получаем разбиение ряда

Самым неформализуемым шагом является шаг группировки. Вся

информация

о каждой из компонент X, содержится в собственном числе Я,, а

также в собственном С/, и факторном К, векторах. Собственный и факторный

вектора называют сингулярными векторами, а совокупность (л/я7,[/.,г,) -

собственной тройкой.

Поиск

компонент для требуемой группировки, главным

образом на основе анализа собственных троек, называется процедурой

идентификации.

Соответственно, для того, чтобы выделить какую-то составляющую ряда

или

отделить сигнал от шума, необходимо найти соответствующие искомой

составляющей компоненты разложения, сгруппировать их и восстановлением

получить искомый ряд.

Условия, при которых такое разложение и выделение возможно, а также

принципы

и теоретические постулаты, на которые опирается идентификация,

описаны

работах

[92,93,97].

достоинствам

метода

«Гусеница»-88А

относятся следующие:

1. Применимость для достаточно широкого класса рядов.

2. Метод не навязывает изначально какую-либо модель

исследуемого

временного ряда. Но при этом позволяет так разложить ряд на

элементарные составляющие, что по ним оказывается возможным

воссоздать

структуру

ряда, например, выделить тренд или найти

периодические составляющие.

3. Возможность очищать сигнал от шумовой составляющей.